- 2014-04-17 21:21:03 感谢硕士生 伊国辉 整理此文
- 2015-03-05 09:31:31 修正公式错误
- 2016-06-30 09:14:23 增加不同晶系代码. 感谢 吴俊彦 校对公式.
- 2017-04-20 15:15:19 添加正交晶系测试, 投影图代码
- 2017-07-19 10:25:31 添加六方晶系测试, 合并剪切模量代码
背景原理简介
各向异性广泛存在各种材料之中. 什么是各向异性呢? 简单来说, 就是晶体在不同方向有不同的性能. 我们很容易把各向异性和不均匀性混淆, 其实这是两个完全不同的概念. 各向异性就是说材料的性能与方向有关, 而不均匀性是指材料的性能与部位有关. 拿单晶来说, 内部任一点, 结构与性能都是相同的, 但不同方向却有不同的性能.
晶体是各向异性的, 不同方向性能不一样, 而且有着严格的对称性. 这里要说一下, 对称性是一个很了不起的性质, 在数学, 物理学中都有着广泛的应用, 而且在材料性质的分析中也常用到. 多晶材料存在择优取向, 也有一定的各向异性.
各种材料都有弹性, 大多数材料的弹性性质也具有各向异性. 例如, 在立方晶体中[111]方向通常比[100]方向更难压缩(stiff). 当我们对材料施加载荷, 材料会发生相应的形变, 在弹性范围内, 形变遵循胡克(Hook)定律, 即应力与应变是线性关系, 可以表示为 $\s = C \ve$, 其中, $\s$ 是应力, $\ve$ 是应变, $C$ 为杨氏模量(或称弹性模量), 也常用 $E$ 或 $Y$ 来表示.
材料不同方向上弹性模量不同, 我们怎么描述这种不同呢? 最好用数学方法, 建立数学框架, 准确直观地将弹性各项异性描述出来. 下面我们就进行这种数学的描述. 本人数学水平有限, 不能一步一步推导, 但我们可以简要理解一下推导过程. 弹性各项异性的推导就是利用张量和群论推广胡克定律. 我们先只考虑低阶弹性常数. 考虑二阶的 $C_{ijkl}$, 原来的胡克定律 $\s = C \ve$ 可推广为为矩阵形式
\[\boldsymbol \s =\left( \begin{array}{c} \s_1 \\ \s_2 \\ \s_3 \\ \s_4 \\ \s_5 \\ \s_6 \end{array} \right) =\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ C_{21} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ C_{31} & C_{32} & C_{33} & C_{34} & C_{35} & C_{36} \\ C_{41} & C_{42} & C_{43} & C_{44} & C_{45} & C_{46} \\ C_{51} & C_{52} & C_{53} & C_{54} & C_{55} & C_{56} \\ C_{61} & C_{62} & C_{63} & C_{64} & C_{65} & C_{66} \\ \end{bmatrix} \left( \begin{array}{c} \ve_1 \\ \ve_2 \\ \ve_3 \\ \ve_4 \\ \ve_5 \\ \ve_6 \end{array} \right) =\mathbf C \boldsymbol \ve\]可以证明, 刚度矩阵 $\mathbf C$ 为对称阵, $C_{ij}=C_{ji}$. 因此, 独立张量元数目至多只有21个. 晶系的对称性越高, 独立的张量元数目就越少. 需要指出的是, $C_{ij}$ 的数目只与晶系有关, 而与晶系中具体的对称类型无关.
$\mathbf C$ 的逆矩阵 $\mathbf S$ 称为柔顺矩阵. 利用 $\mathbf S$ 可得到杨氏弹性模量的一般表达式. 我们用与[100], [010], [001]三个晶向的方向余弦来表示任意方向的杨氏模量. 设 $l_1, l_2, l_3$ 为空间某一方向与晶体主轴的方向余弦, 空间任一方向的杨氏模量 $E$ 的大小只与方向有关, 具体表达式如下
\[\alg 1/E= S_{11} l_1^4 &+ 2 S_{12} (l_1 l_2)^2 &+ 2S_{13} (l_1 l_3)^2 &+ 2 S_{14} (l_2 l_3 l_1^2) &+ 2 &S_{15} (l_3 l_1^3) &+ 2 &S_{16} (l_2 l_1^3) \\ &+ S_{22} l_2^4 &+ 2S_{23} (l_2 l_3)^2 &+ 2 S_{24} (l_3 l_2^3) &+ 2 &S_{25} (l_1 l_3 l_2^2) &+ 2 &S_{26} (l_1 l_2^3) \\ & &+ S_{33} l_3^4 &+ 2 S_{34} (l_2 l_3^3) &+ 2 &S_{35} (l_1 l_3^3) &+ 2 &S_{36} (l_1 l_2 l_3^2) \\ & & &+ S_{44} (l_2 l_3)^2 &+ 2 &S_{45} (l_1 l_2 l_3^2) &+ 2 &S_{46} (l_1 l_3 l_2^2) \\ & & & &+ &S_{55} (l_1 l_3)^2 &+ 2 &S_{56} (l_2 l_3 l_1^2) \\ & & & & & &+ &S_{66} (l_1 l_2)^2 \\ \ealg\]写为矩阵元素加和的形式为
\[\alg 1/E &= \Sum_{m=1}^3 \Sum_{n=1}^3 \Sum_{p=1}^3 \Sum_{q=1}^3 S_{mnpq} l_m l_n l_p l_q \\ &=\Sum(\mathbf S \mathbf L^T \mathbf L) \\ \mathbf L &=(l_1^2, l_2^2, l_3^3, l_2l_3, l_1l_3, l_1l_2) \ealg\]一种较对称, 方便推导的形式为
\[\alg 1/E&=S_{11} l_1^4 + S_{22} l_2^4 + S_{33} l_3^4 \\ &+ (S_{44}+2S_{23}) (l_2l_3)^2 + (S_{55}+2S_{13}) (l_1l_3)^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \\ &+ 2\left[(S_{14}+S_{56}) l_1^2 +S_{24} l_2^2 + S_{34} l_3^2\right] l_2 l_3 \\ &+ 2\left[S_{15} l_1^2 +(S_{25} +S_{46}) l_2^2 + S_{35} l_3^2 \right] l_1 l_3 \\ &+ 2\left[S_{16} l_1^2 +S_{26} l_2^2 + (S_{36}+S_{45}) l_3^2\right] l_1 l_2 \ealg\]这三种不同的表达形式, 可根据需要选择使用.
不同晶系的杨氏弹性模量
上面杨氏弹性模量的公式有些复杂, 好在除三斜晶系外, 大多数晶体都具有对称性. 考虑到晶体的对称性, 某些弹性常数必定为零, 而某些则相等, 所以对具有对称性的晶体, 相应的的杨氏模量公式简单些. 下面两张图总结了不同晶系刚度矩阵和柔顺矩阵的特点, 以及不同晶系杨氏弹性模量的公式, 后者为许多文献所引用.
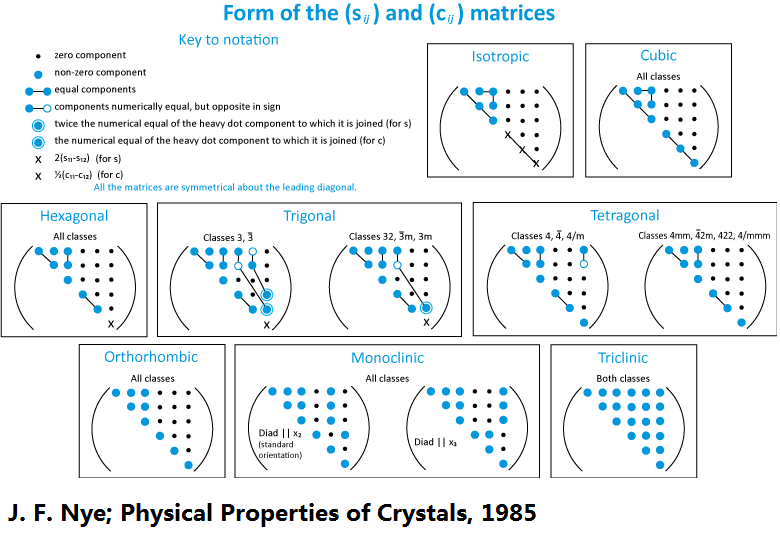

1 三斜晶系(Triclinic system)
三斜晶系是所有七大晶系中对称性最低的晶系, 因此拥有最多的独立矩阵元, 其形式为:
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ & & C_{33} & C_{34} & C_{35} & C_{36} \\ & & & C_{44} & C_{45} & C_{46} \\ & & & & C_{55} & C_{56} \\ & & & & & C_{66} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & S_{14} & S_{15} & S_{16} \\ & S_{22} & S_{23} & S_{24} & S_{25} & S_{26} \\ & & S_{33} & S_{34} & S_{35} & S_{36} \\ & & & S_{44} & S_{45} & S_{46} \\ & & & & S_{55} & S_{56} \\ & & & & & S_{66} \\ \end{bmatrix}\]共有21个独立的矩阵元, 杨氏模量
\[\alg 1/E&=S_{11} l_1^4 + S_{22} l_2^4 + S_{33} l_3^4 \\ &+ (S_{44}+2S_{23}) (l_2l_3)^2 + (S_{55}+2S_{13}) (l_1l_3)^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \\ &+ 2\left[(S_{14}+S_{56}) l_1^2 +S_{24} l_2^2 + S_{34} l_3^2\right] l_2 l_3 \\ &+ 2\left[S_{15} l_1^2 +(S_{25} +S_{46}) l_2^2 + S_{35} l_3^2 \right] l_1 l_3 \\ &+ 2\left[S_{16} l_1^2 +S_{26} l_2^2 + (S_{36}+S_{45}) l_3^2\right] l_1 l_2 \ealg\]2 单斜晶系(Monoclinic system)
考虑对称性后, 单斜晶系有13个独立的矩阵单元:
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & C_{15} & 0 \\ & C_{22} & C_{23} & 0 & C_{25} & 0 \\ & & C_{33} & 0 & C_{35} & 0 \\ & & & C_{44} & 0 & C_{46} \\ & & & & C_{55} & 0 \\ & & & & & C_{66} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & S_{15} & 0 \\ & S_{22} & S_{23} & 0 & S_{25} & 0 \\ & & S_{33} & 0 & S_{35} & 0 \\ & & & S_{44} & 0 & S_{46} \\ & & & & S_{55} & 0 \\ & & & & & S_{66} \\ \end{bmatrix}\] \[\alg 1/E&=S_{11} l_1^4 + S_{22} l_2^4 + S_{33} l_3^4 \\ &+ (S_{44}+2S_{23}) (l_2l_3)^2 + (S_{55}+2S_{13}) (l_1l_3)^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \\ &+ 2\left[S_{15} l_1^2 +(S_{25} +S_{46}) l_2^2 + S_{35} l_3^2 \right] l_1 l_3 \ealg\]3 正交晶系(Orthorhombic system)
正交晶系拥有相当高的对称性, 其独立矩阵元的数目为9个.
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ & C_{22} & C_{23} & 0 & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{55} & 0 \\ & & & & & C_{66} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ & S_{22} & S_{23} & 0 & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{55} & 0 \\ & & & & & S_{66} \\ \end{bmatrix}\] \[\alg 1/E&=S_{11} l_1^4 + S_{22} l_2^4 + S_{33} l_3^4 \\ &+ (S_{44}+2S_{23}) (l_2l_3)^2 + (S_{55}+2S_{13}) (l_1l_3)^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \ealg\]4 四方晶系(Tetragonal system)
4.1 四方晶系 $4, \bar 4, 4/m$
对于具有 $4, \bar4, 4/m$ 对称操作的四方晶系, 其独立矩阵元的数目为7个:
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & C_{16} \\ & C_{11} & C_{13} & 0 & 0 & -C_{16} \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{44} & 0 \\ & & & & & C_{66} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & S_{16} \\ & S_{11} & S_{13} & 0 & 0 & -S_{16} \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{44} & 0 \\ & & & & & S_{66} \\ \end{bmatrix}\] \[\alg 1/E&=S_{11} (l_1^4 + l_2^4) + S_{33} l_3^4 \\ &+ (S_{44}+2S_{13}) (l_1^2+l_2^2) l_3^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \\ &+ 2 S_{16} (l_1^2 - l_2^2) l_1 l_2 \ealg\]4.2 四方晶系 $422, 4mm, \bar 42m, 4/mmm$
对于具有 $422, 4mm, \bar 42m, 4/mmm$ 对称操作的四方晶系, 独立矩阵元的数目仅为6个:
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ & C_{11} & C_{13} & 0 & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{44} & 0 \\ & & & & & C_{66} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ & S_{11} & S_{13} & 0 & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{44} & 0 \\ & & & & & S_{66} \\ \end{bmatrix}\] \[\alg 1/E&=S_{11} (l_1^4 + l_2^4) + S_{33} l_3^4 \\ &+ (S_{44}+2S_{13}) (l_1^2+l_2^2) l_3^2 + (S_{66}+2S_{12}) (l_1l_2)^2 \ealg\]5 三方晶系(Trigonal system)
5.1 三方晶系 $3, \bar 3$
三方晶系 $3, \bar 3$ 的独立矩阵元的数目为7个.
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & 0 \\ & C_{11} & C_{13} & -C_{14} & -C_{15} & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & -C_{15} \\ & & & & C_{44} & C_{14} \\ & & & & & {C_{11}-C_{12} \over 2} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & S_{14} & S_{15} & 0 \\ & S_{11} & S_{13} & -S_{14} & -S_{15} & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & -S_{15} \\ & & & & S_{44} & S_{14} \\ & & & & & 2(S_{11}-S_{12}) \\ \end{bmatrix}\] \[\alg 1/E &=S_{11}(l_1^4+l_2^4+2l_1^2l_2^2)+S_{33} l_3^4 \\ &+(S_{44}+2S_{13})(l_1^2+l_2^2) l_3^2+2S_{14}(3l_1^2-l_2^2) l_2 l_3 +2S_{15}(l_1^2-3l_2^2) l_1 l_3 \\ &=S_{11}(1-l_3^2)^2+S_{33} l_3^4 \\ &+(S_{44}+2S_{13})(1-l_3^2) l_3^2 +2S_{14}(3l_1^2-l_2^2) l_2 l_3 +2S_{15}(l_1^2-3l_2^2) l_1 l_3 \ealg\]5.2 三方晶系 $32, 3m, \bar 3m$
三方晶系 $32, 3m, \bar 3m$ 独立矩阵元的数目为6个.
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & 0 & 0 \\ & C_{11} & C_{13} & -C_{14} & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{44} & C_{14} \\ & & & & & {C_{11}-C_{12} \over 2} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & S_{14} & 0 & 0 \\ & S_{11} & S_{13} & -S_{14} & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{44} & S_{14} \\ & & & & & 2(S_{11}-S_{12}) \\ \end{bmatrix}\] \[\alg 1/E &=S_{11}(l_1^4+l_2^4+2l_1^2l_2^2)+S_{33} l_3^4 \\ &+(S_{44}+2S_{13})(l_1^2+l_2^2) l_3^2+2S_{14}(3l_1^2-l_2^2) l_2 l_3 \\ &=S_{11}(1-l_3^2)^2+S_{33} l_3^4 \\ &+(S_{44}+2S_{13})(1-l_3^2) l_3^2 +2S_{14}(3l_1^2-l_2^2) l_2 l_3 \ealg\]6 六方晶系(Hexagonal system)
六方晶系共有5个独立的矩阵元.
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ & C_{11} & C_{13} & 0 & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{44} & 0 \\ & & & & & {C_{11}-C_{12} \over 2} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ & S_{11} & S_{13} & 0 & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{44} & 0 \\ & & & & & 2(S_{11}-S_{12}) \\ \end{bmatrix}\] \[\alg 1/E &= S_{11}(l_1^4+l_2^4+2l_1^2l_2^2)+S_{33} l_3^4+(S_{44}+2S_{13})(l_1^2+l_2^2) l_3^2 \\ &= S_{11} (1-l_3^2)^2 + S_{33} l_3^4 + (S_{44}+2S_{13}) (1-l_3^2)l_3^2 \ealg\]7 立方晶系(Cubic system)
立方晶系是所有晶系中对称度最高的晶系, 其独立矩阵元数目仅为3个, $C_{11}, C_{12}, C_{44}$
\[\mathbf C=\begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\ & C_{11} & C_{12} & 0 & 0 & 0 \\ & & C_{11} & 0 & 0 & 0 \\ & & & C_{44} & 0 & 0 \\ & & & & C_{44} & 0 \\ & & & & & C_{44} \\ \end{bmatrix}\] \[\mathbf S=\begin{bmatrix} S_{11} & S_{12} & S_{12} & 0 & 0 & 0 \\ & S_{11} & S_{12} & 0 & 0 & 0 \\ & & S_{11} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ & & & & S_{44} & 0 \\ & & & & & S_{44} \\ \end{bmatrix}\] \[\alg 1/E&=S_{11}(l_1^4+l_2^4+l_3^4)+(S_{44}+2S_{12})(l_1^2 l_2^2+l_1^2 l_3^2+l_2^2 l_3^2) \\ &=S_{11}-2(S_{11}-S_{12}-{S_{44}\over 2}) (l_1^2l_2^2+l_2^2l_3^2+l_1^2l_3^2) \ealg\]杨氏模量的极值
对于立方晶体, 我们可以用与[100], [010], [001]三个晶向的方向余弦来表示任意方向的杨氏模量, 结果如下
\[\begin{align} {1 \over E} &=S_{11}-2( S_{11}-S_{12}-{S_{44} \over 2} )(l_1^2l_2^2+l_2^2l_3^2+l_3^2l_1^2) \\ &= S_{11}+(1-A)S_{44}(l_1^2l_2^2+l_2^2l_3^2+l_3^2l_1^2) \\ A &= 2 {S_{11}-S_{12} \over S_{44}} \\ \mathbf S &= \mathbf C^{-1} \end{align}\]其中 $S_{11}, S_{12}, S_{44}$ 分别为立方晶体的三个独立的弹性柔顺系数, 柔顺矩阵 $S$ 与弹性矩阵 $C$ 的矩阵互为逆矩阵. $l_1, l_2, l_3$ 为空间某一方向与晶体主轴的方向余弦. $A$ 为各向异性值. 因此, 知道了三个柔顺弹性常数的值, 即可求得空间任一方向的杨氏模量 $E$, $E$ 的大小只与方向有关.
由于 $l_1^2+l_2^2+l_3^2=1, l_1, l_2, l_3 \in [0,1]$, 可以知道杨氏模量的两个极值为
\[\begin{align} E_1 &={1 \over S_{11} } \\ E_2 &={1 \over S_{11}+{1\over 3}(1-A)S_{44}} \end{align}\]前者对应于坐标轴方向, 后者对应于体对角线方法. 根据各向异性值 $A$ 与1的大小不同, 相应于极小或极大值.
对于其他晶系杨氏模量的极值, 不易得到解析公式, 直接使用数值方法搜索即可.
杨氏弹性模量各向异性的图示
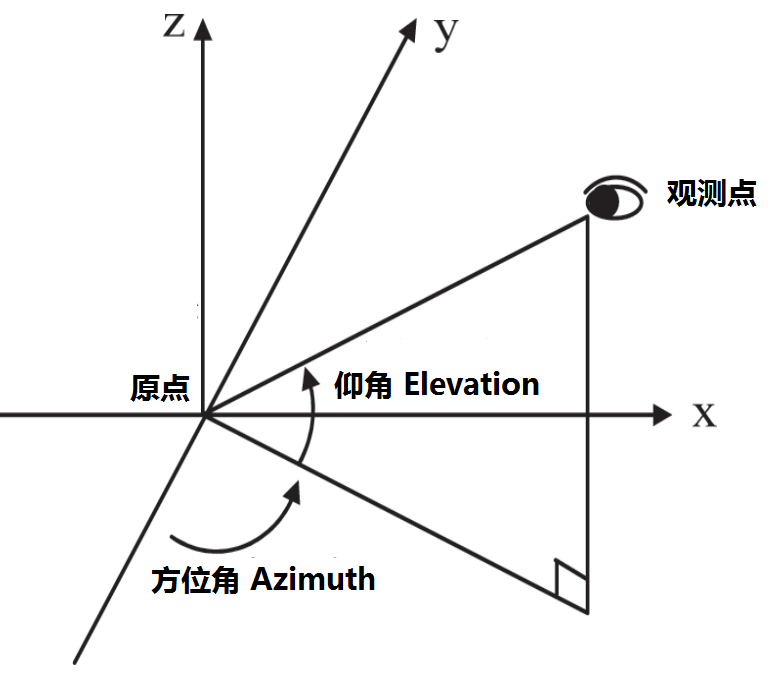
为了直观地表达弹性模量的各向异性, 人们常常将其用三维图来表示. 这种各向异性的直观图示方法具有一般性, 在科学数据可视化中经常遇到. 量子化学中常用的原子轨道的角度分布图就是一例. 具体原理是, 在球坐标系 $(r,\q, \f)$ 中, 对仅依赖于方向的函数 $F(\q, \f)$ 中, 做曲面 $r=F(\q, \f)$. 显然, 当 $F$ 为常数时, 此曲面为球面, 各个方向函数值相同, 不存在各向异性; 当 $F$ 随 $(\q,\f)$ 变化时, 曲面便可表示出函数值的变化.
mathematica中可使用球坐标绘图函数SphericalPlot3D来做出这种图, 很多文献中的图就是利用这个函数做的, 请参考这个函数的说明和相应的弹性模量示例.
考虑到Matlab使用更广泛些, 下面给出基于Matlab的绘图方法.
利用Matlab绘制各向异性图时, 有两种实现方法. 一种是利用球坐标绘图, 像mathematica那样. 虽然Matlab没有球坐标绘图函数, 但可以先将球坐标转换为直角坐标然后再绘图, 也不是很麻烦. 另一种方法是直接使用直角坐标, 利用等值面函数, 绘制函数 $r-E=0$ 的等值面.
下面的代码绘制几种金属的杨氏模量三维各向异性曲面, 弹性常数来源于这里.
代码见剪切模量博文
注意
- matlab默认的渲染颜色取决于Z轴大小, 这不符合我们的要求, 因为我们需要用颜色表示E的大小, 这样图形更直观.
- matlab球坐标转换函数使用的球坐标采用数学约定, 与物理上常用的不同, 使用仰角El, 而非俯视角 $\q$, $El+\q=\p/2$
- 不同晶系杨氏模量的表达式不同, 只要把代码里E的表达式修改成相应的方程即可.
- 杨氏模量在某一平面内的截面图形可利用极坐标或直角坐标绘制, 原理类似.
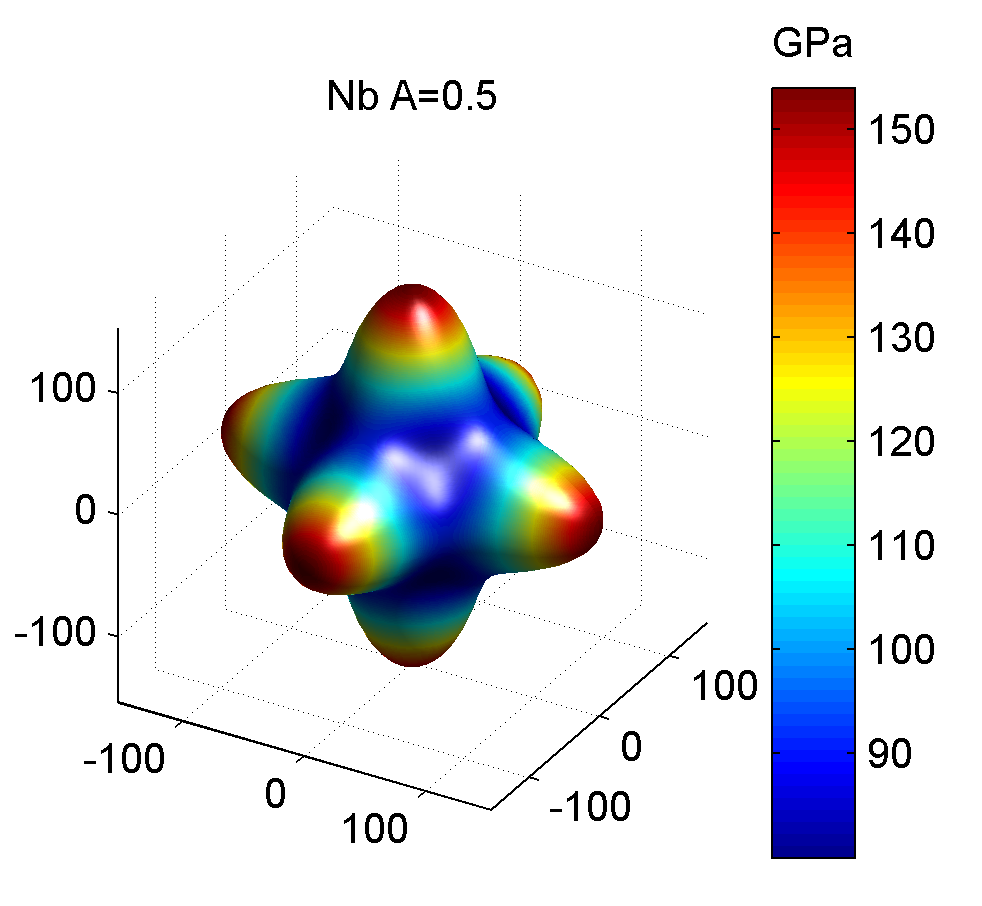
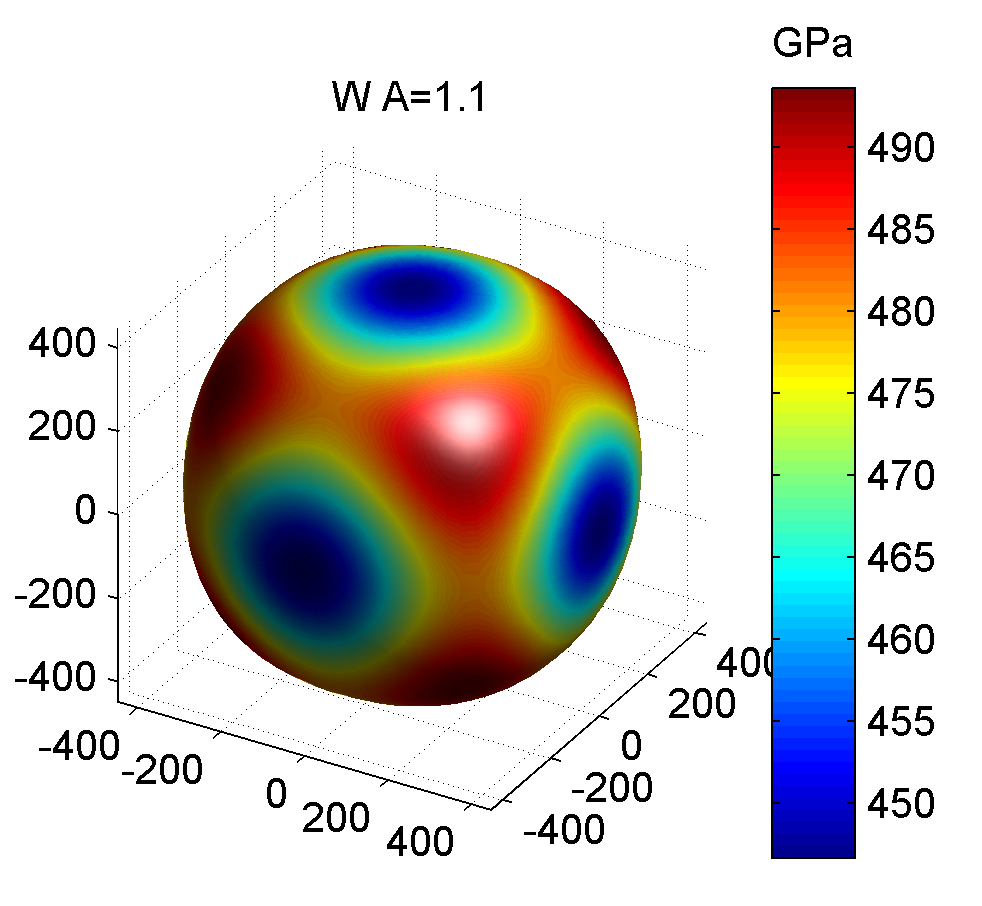
为了让大家有一个更直观的了解, 我们把具有不同各向异性值的立方金属选取具有代表性几个, 列于下表
| 金属 | C11 | C12 | C44 | S11 | S12 | S44 | A | Emin | Emax |
|---|---|---|---|---|---|---|---|---|---|
| 铌Nb | 240.20 | 125.60 | 28.20 | 0.0065 | -0.0022 | 0.0355 | 0.49 | 80.01 | 153.95 |
| 钨W | 522.40 | 160.80 | 204.40 | 0.0025 | -0.0007 | 0.0062 | 1.13 | 446.71 | 493.65 |
| 铝Al | 107.30 | 60.90 | 28.30 | 0.0158 | -0.0057 | 0.0353 | 1.22 | 63.20 | 75.57 |
| 铂Pt | 346.70 | 250.70 | 76.50 | 0.0073 | -0.0031 | 0.0131 | 1.59 | 136.29 | 210.51 |
| 铁Fe | 231.40 | 134.70 | 116.40 | 0.0076 | -0.0028 | 0.0086 | 2.41 | 132.28 | 283.34 |
| 银Ag | 124.00 | 93.40 | 46.10 | 0.0229 | -0.0098 | 0.0217 | 3.01 | 43.75 | 120.44 |
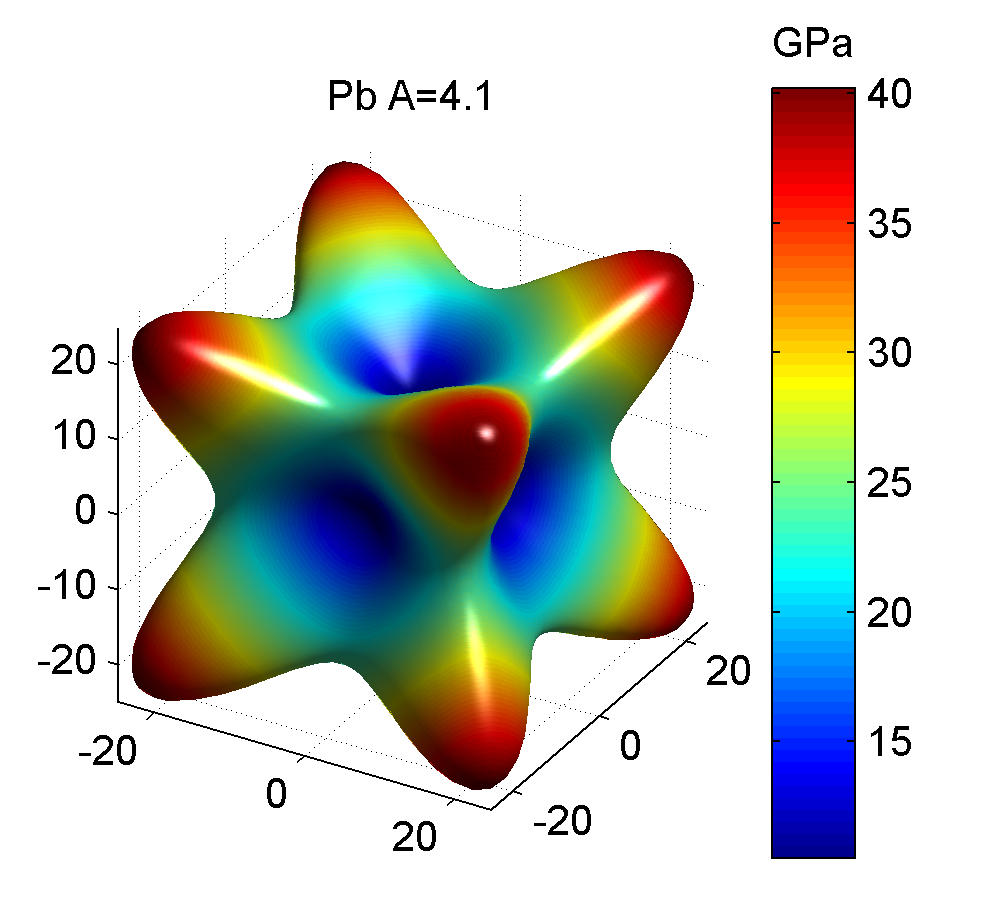
| 铅Pb | 49.50 | 42.30 | 14.90 | 0.0951 | -0.0438 | 0.0671 | 4.14 | 10.52 | 40.23 |
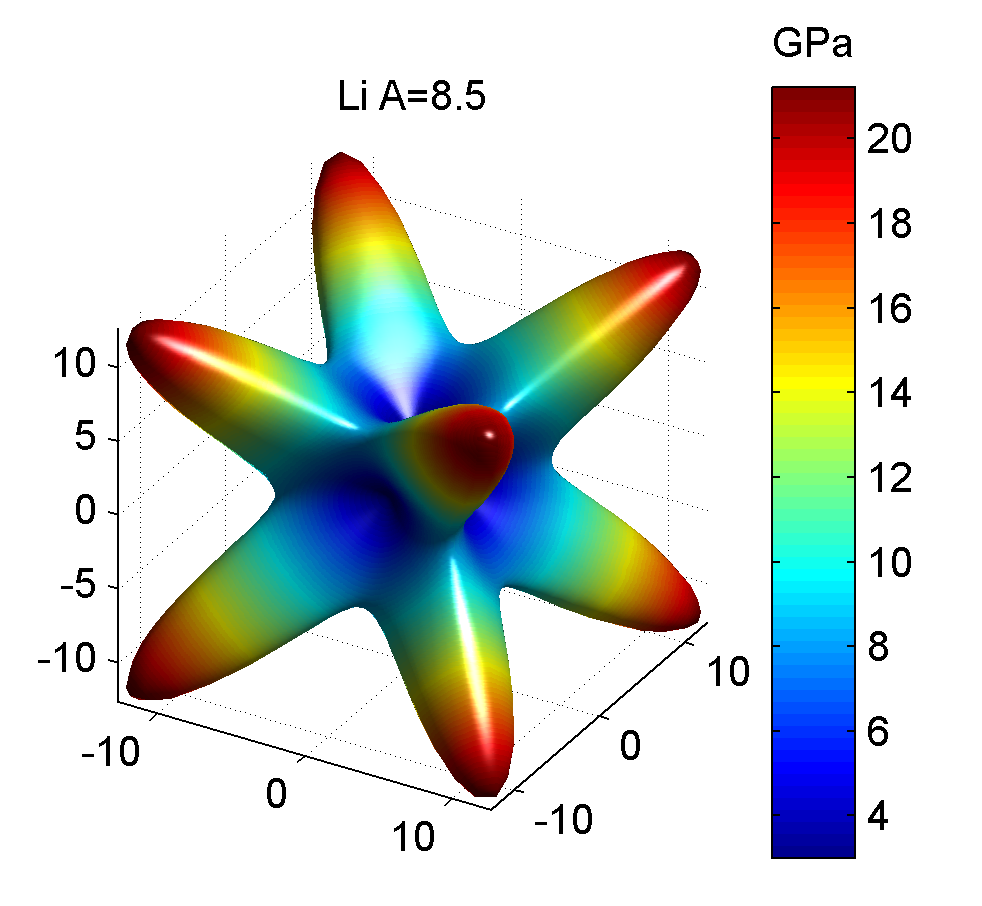
| 锂Li | 13.50 | 11.44 | 8.78 | 0.3328 | -0.1526 | 0.1139 | 8.52 | 3.00 | 21.23 |
相应的三维杨氏模量图如下
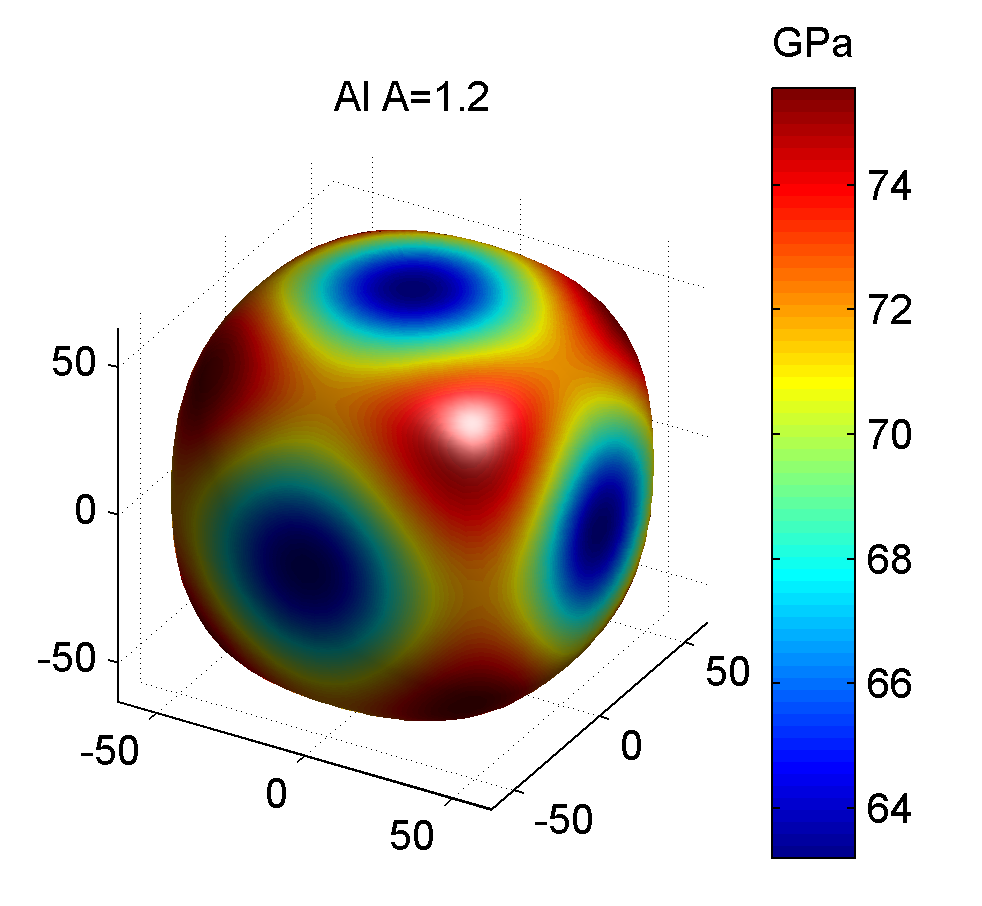
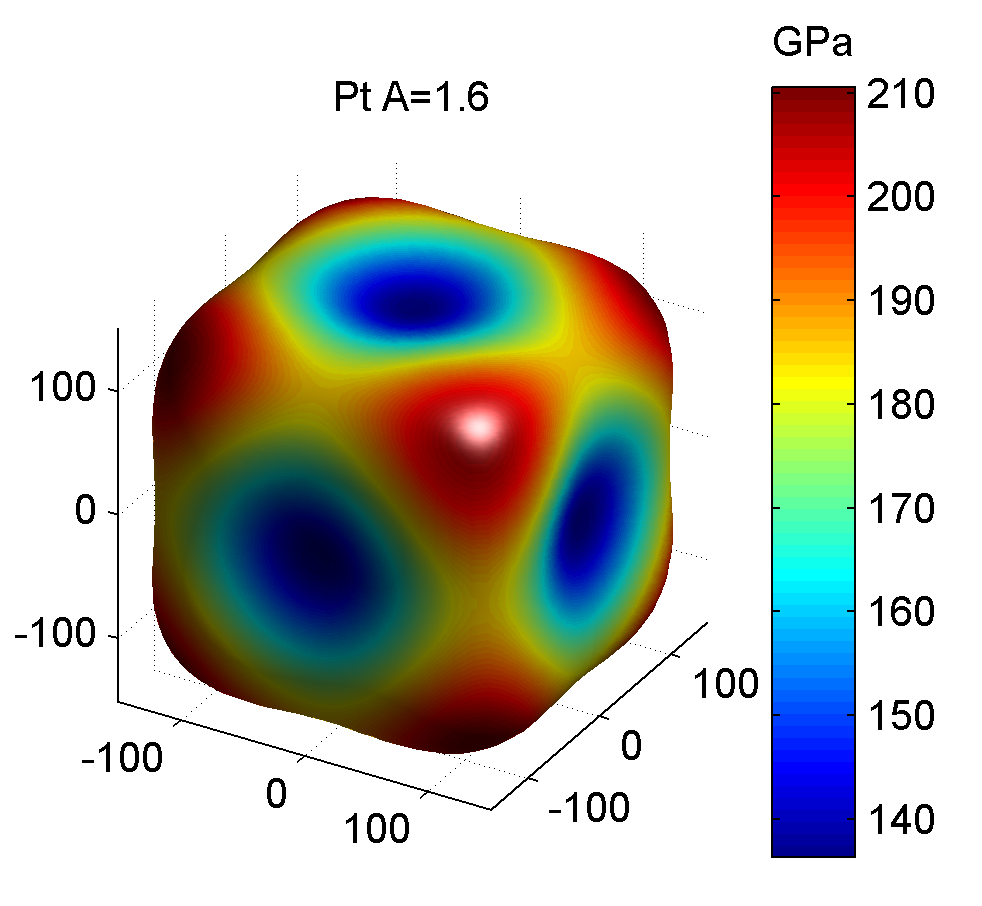
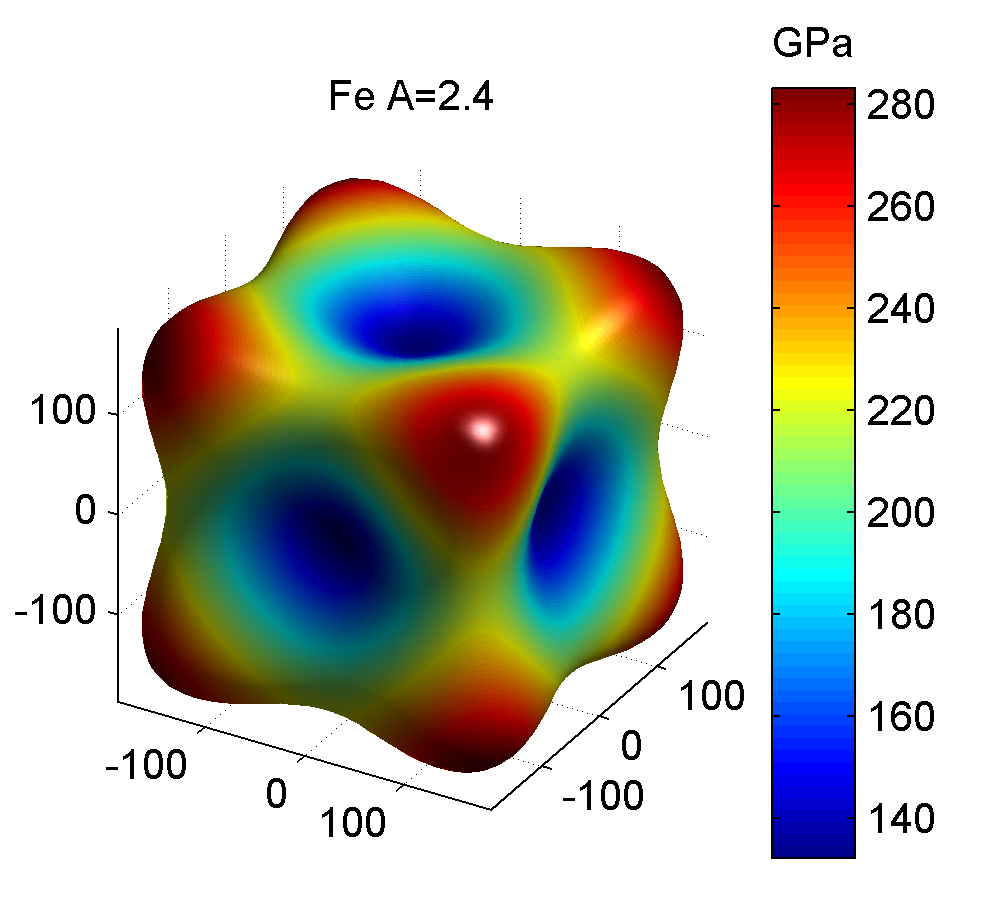
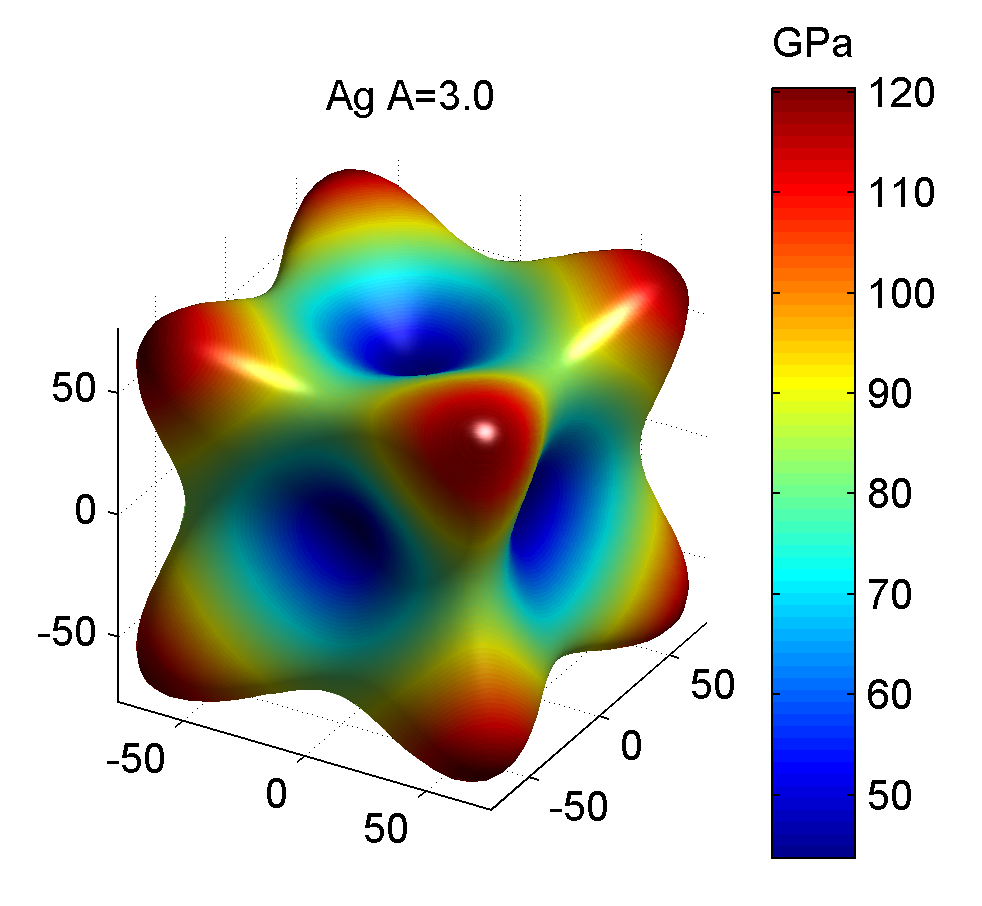
参考资料
- T. C. T. Ting; On Anisotropic Elastic Materials for which Young’s Modulus E(n) is Independent of n or the Shear Modulus G(n,m) is Independent of n and m; J Elasticity 81(3):271-292, 2006; 10.1007/s10659-005-9016-2
- Kevin M. Knowles, Philip R. Howie; The Directional Dependence of Elastic Stiffness and Compliance Shear Coefficients and Shear Moduli in Cubic Materials; J Elast 120(1):87-108, 2014; 10.1007/s10659-014-9506-1
- Matlab绘图高级部分
- 科学计算可视化: 三维流场绘图
- Applied Mechanics of Solids: Constitutive Models Relations between Stress and Strain
- 球坐标
评论
- 2016-09-30 12:50:05
Yabei版主,想问一下matlab程序里面第一句function aniso, 这个部分代码是啥? -
2016-09-30 13:20:09
Jerkwin定义一个函数, 以方便在命令行中调用. - 2017-03-28 23:34:19
kuner楼主,您好,请问有其它的四方体系的代码吗,谢谢 -
2017-03-30 23:49:40
Jerkwin代码可以用于任何晶系, 只要给出相应的C就可以了. - 2017-04-13 22:26:27
kuner好的,谢谢,已经学习并测试,与例子一致。感谢。另外,对于不同晶面上(比如在XY.YZ、XZ)的投影图,能否指点一下代码,捣鼓了好久,没有成功,谢谢了。 -
2017-04-14 08:28:23
Jerkwin% 作模量的某一切面图 那句就是做切面的, 你取消注释测试下就明白了 - 2017-04-13 22:30:27
kuner对于Tetragonal system中的E的表达式,有一项与文献(1985书)不同,是否是笔误? - 2017-04-14 08:21:01
Jerkwin二者是一致的, 你有疑问的那项书中写为 L3^2 (1-L3^2) = L3^2 (L1^2+L2^2), 因为L1, L2和L3三者组成单位向量, 其模L^2 = L1^2+L2^2+L3^3 = 1. -
2017-04-16 18:33:49
kuner谢谢,是的,我后来也搞明白了,感谢 - 2017-04-13 23:05:53
kuner“”matlab默认的渲染颜色取决于Z轴大小, 这不符合我们的要求, 因为我们需要用颜色表示E的大小, 这样图形更直观.”,这话什么意思,如何用颜色表示E的大小呢?谢谢 - 2017-04-14 08:25:25
Jerkwin颜色映射图, 首先要确定根据什么数值来决定颜色, matlab默认根据曲面的z坐标来确定颜色, 所以如果你画出来就是从下到上均匀过渡的颜色, 而我们需要的不是这种, 我们要让matlab根据每点E的大小来确定颜色, 这样颜色标尺表示的才是E的大小. -
2017-04-16 18:33:20
kuner是的。我测试了一下,可以得到您微博中的各个单质金属的三维图,颜色差不多,标尺大小、颜色也类似,也就是说图中的颜色已经表示了E或G的大小了,是这意思吧?谢谢 - 2017-04-18 23:42:35
kuner请问楼主,我还是不能画出二维投影图的边线图,我看好多文献都是画出来了的,就是那个类似于园或椭圆的那个东西,园边线内无任何图色的 -
2017-04-21 04:34:08
Jerkwin修订了代码, 其中有说明, 去掉注释就能得到你需要的图. - 2017-04-18 12:37:20
Lily楼主您好,如果不是立方晶系,是四方、六方或者正交晶系,需要修改E公式吗?我测试的正交晶系和六方晶系,修改E公式后和别人的图不一样,把E公式注释掉后也不对 - 2017-04-18 21:16:43
Jerkwin不需要修改, 默认的公式适用于任何晶系. 如果你确定自己操作无误, 请给出具体的数值和对照图. - 2017-04-19 10:13:09
Lily正交晶系:C11=115.9 ;C12=35.3; C13=46.8;C22=174.1;C23=38.7;C33=153.1;C44=50.9;C55=70.2;C66=26.6 不知道怎么传图,我把参考图放在链接里了,麻烦了http://pan.baidu.com/s/1eS5RPfG -
2017-04-21 04:33:16
Jerkwin我修订了代码, 默认就使用你说的数值, 请测试对比. -
2017-04-21 22:06:29
Lily进行了测试,四方、六方和正交都没问题,非常感谢! - 2017-04-22 13:44:06
Lily另外关于楼下kuner提到的二维投影图的边线图的问题,我按照您说的操作之后得到的是中间有颜色和网格线的图,是否可以只得到轮廓图呢?类似于链接中的图http://pan.baidu.com/s/1o8TspMM - 2017-04-24 11:02:28
Jerkwin注释掉新添加的投影代码, 再照我的说明做
