2014-07-17 15:10:54
Schrödinger方程
\[[-\frac{\hbar^2}{2\mu}{\nabla^{2}}+V(r)]\Psi (r,\theta ,\varphi )=E\Psi (r,\theta ,\varphi )\]其中
\[{\nabla^{2}}=\frac{1}{r^{2}}[\frac{\partial }{\partial r}({r^{2}}\frac{\partial }{\partial r})+\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }(\sin \theta \frac{\partial }{\partial \theta })+\frac{1}{\sin {\theta^{2}}}\frac{\partial }{\partial {\phi^{2}}}]\equiv \frac{1}{r^{2}}({\nabla_{r}}^{2}+{\nabla_{\theta \phi}^{2}})\] \[{\nabla^{2}}\Psi (r,\theta ,\varphi )=-\frac{2\mu (E-V)}{\hbar^{2}}\Psi (r,\theta ,\varphi )\] \[\frac{1}{r^{2}}({\nabla_{r}}^{2}+{\nabla_{\theta \phi }}^{2})\Psi (r,\theta ,\varphi )=-\frac{2\mu (E-V)}{\hbar^{2}}\Psi (r,\theta ,\varphi )\] \[({\nabla_{r}}^{2}+{\nabla_{\theta \phi }}^{2})\Psi (r,\theta ,\varphi )=-\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}\Psi (r,\theta ,\varphi )\]分离变量, 设 $\Psi (r,\theta ,\varphi )=R(r)Y(\theta ,\varphi )$
\[[{\nabla_{r}}^{2}+{\nabla_{\theta \phi }}^{2}]R(r)Y(\theta ,\phi )=-\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}R(r)Y(\theta ,\phi )\] \[Y(\theta ,\phi ){\nabla_{r}}^{2}R(r)+R(r){\nabla_{\theta \phi }}^{2}Y(\theta ,\phi )=-\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}R(r)Y(\theta ,\phi )\]两边同除 $\Psi (r,\theta ,\varphi )=R(r)Y(\theta ,\phi )$
\[\frac{1}{R(r)}{\nabla_{r}}^{2}R(r)+\frac{1}{Y(\theta ,\phi )}{\nabla_{\theta \phi }}^{2}Y(\theta ,\phi )=-\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}\]令 \(\frac{1}{R(r)}{\nabla_{r}}^{2}R(r)+\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}=-\frac{1}{Y(\theta ,\phi )}{\nabla_{\theta \phi }}^{2}Y(\theta ,\phi )=\lambda\)
有角度部分方程 ${\nabla_{\theta \phi }}^{2}Y(\theta ,\phi )+\lambda Y(\theta ,\phi )=0$
其解为球谐函数 $Y(\theta ,\phi )={Y_{lm}}(\theta ,\phi ), \lambda =l(l+1), l=0,1,2,3……$
径向部分方程 $\frac{1}{R(r)}{\nabla_{r}}^{2}R(r)+\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}=\lambda$
${\nabla_{r}}^{2}R(r)+[\frac{2\mu (E-V){r^{2}}}{\hbar^{2}}-\lambda ]R(r)=0$
$\frac{1}{r^{2}}{\nabla_{r}}^{2}R(r)+[-\frac{\lambda }{r^{2}}+\frac{2\mu (E-V)}{\hbar^{2}}]R(r)=0$
$\frac{1}{r^{2}}\frac{d}{dr}[{r^{2}}\frac{dR(r)}{dr}]+[-\frac{\lambda }{r^{2}}+\frac{2\mu (E-V)}{\hbar^{2}}]R(r)=0$
令 $R(r)=\frac{u(r)}{r}$, $\frac{dR(r)}{dr}=\frac{r\frac{du(r)}{dr}}{r^{2}}=\frac{r{u}’-u}{r^{2}}$
$\frac{d}{dr}[{r^{2}}\frac{dR(r)}{dr}]=\frac{d}{dr}(r{u}’-u)=r{u}’’+{u}’-{u}’=r{u}’’$
$\frac{1}{r^{2}}\frac{d}{dr}[{r^{2}}\frac{dR(r)}{dr}]=\frac{1}{r^{2}}r{u}’’=\frac{1}{r}{u}’’$
$\frac{1}{r}{u}’’+[-\frac{\lambda }{r^{2}}+\frac{2\mu (E-V)}{\hbar^{2}}]\frac{u(r)}{r}=0$
${u}’’+[-\frac{\lambda }{r^{2}}+\frac{2\mu (E-V)}{\hbar^{2}}]u(r)=0$
库仑势 \(V(r)=-\frac{Z{e^{2}}}{4\pi {\varepsilon_{0}}r}\), 更一般设 \(V(r)=-\frac{\kappa Z{e^{2}}}{4\pi {\varepsilon_{0}}r}\)
${u}’’+[\frac{2\mu (E-V)}{\hbar^{2}}-\frac{l(l+1)}{r^{2}}]u=0$
${u}’’+[\frac{2\mu }{\hbar^{2}}E+\frac{2\mu }{\hbar^{2}}\frac{\kappa Z{e^{2}}}{4\pi {\varepsilon_{\circ }}r}-\frac{l(l+1)}{r^{2}}]u=0$
只考虑束缚解, $E<0$, 令 $-{\beta^{2}}=\frac{2\mu E}{\hbar^{2}}$, $\alpha =\frac{2\mu \kappa Z{e^{2}}}{4\pi {\varepsilon_{0}}{\hbar^{2}}}$
得 ${u}’’+[-{\beta^{2}}+\frac{\alpha }{r}-\frac{l(l+1)}{r^{2}}]u=0$
先考虑其渐近解, 当 $r\to \infty$ 时, ${u}’’-{\beta^{2}}u=0$, 得 $u={c_{1}}{e^{-\beta r}}(\,{e^{\beta r}})$
当 $r\to 0$ 时, 设 $r\sim {r^{s}}$, 有
$s(s-1){r^{s-2}}+(-{\beta^{2}}{r^{s}}+\alpha {r^{s-1}}-\lambda {r^{s-1}})=0$
除以 ${r^{s-2}}$
$s(s-1)-\frac{\beta^{2}{r^{s}}}{r^{s-2}}+\alpha r-\lambda =s(s-1)-{\beta^{2}}{r^{2}}+\alpha r-\lambda =0$
$s(s-1)-\lambda =0$
$s(s-1)-l(l+1)=0$ 得 $s=l+1(s=-l)$
设方程解为 \(u(r)={r^{l+1}}{e^{-\beta r}}f(r)\)
\[{u}''={r^{l-1}}{e^{-\beta r}}\left\{ {r^{2}}{f}''(r)+2r(l+1-\beta r){f}'(r)+[{\beta^{2}}{r^{2}}+(l+1)(l-2\beta r)]f(r) \right\}\] \[\begin{align} [-{\beta^{2}}+\frac{\alpha }{r}-\frac{l(l+1)}{r^{2}}]u &= [-{\beta^{2}}+\frac{\alpha }{r}-\frac{l(l+1)}{r^{2}}]{r^{l+1}}{e^{-\beta r}}f(r) \\ &= [-{\beta^{2}}{r^{2}}+\alpha r-l(l+1)]{r^{l-1}}{e^{-\beta r}}f(r) \end{align}\] \[{u}''+[-{\beta^{2}}+\frac{\alpha }{r}-\frac{l(l+1)}{r^{2}}]u \\ ={r^{l-1}}{e^{-\beta r}} \\ \left\{ {r^{2}}{f}''(r)+2r(l+1-\beta r){f}'(r) +[{\beta^{2}}{r^{2}}+(l+1)(l-2\beta r)-{\beta^{2}}{r^{2}}+\alpha r-l(l+1)]f(r) \right\} \\ =0\] \[{r^{2}}{f}''(r)+2r(l+1-\beta r){f}'(r)+r[\alpha -2\beta (l+1)]f(r)=0\] \[r{f}''(r)+2(l+1-\beta r){f}'(r)+[\alpha -2\beta (l+1)]f(r)=0\]令 \(\rho =2\beta r, {f}'(r)=2\beta {f}'(\rho )\), \({f}''(r)=4{\beta^{2}}{f}''(\rho )\)
$4{\beta^{2}}r{f}’’(\rho )+4\beta (l+1-\beta r){f}’(\rho )+[\alpha -2\beta (l+1)]f(\rho )=0$
$2\beta \rho {f}’’(\rho )+4\beta (l+1-\beta r){f}’(\rho )+[\alpha -2\beta (l+1)]f(\rho )=0$
$\rho {f}’’(\rho )+[2(l+1)-\rho ]{f}’(\rho )-[(l+1)-\frac{\alpha }{2\beta }]f(\rho )=0$
合流超几何方程 $x{y}’’+(c-x){y}’-ay=0$
其解为合流超几何函数 \(F(a,c,x)=\sum\limits_{k=0}^{\infty } \frac{(a)_{k}} {(c)_{k}} \frac{x^{k}}{k!}\ \{_{(c)_{k}=c(c+1)...(c+k-1)}^{(a)_{k}=a(a+1)...(a+k-1)}\)
对比可知 $c=2(l+1)$, $a=l+1-\frac{\alpha }{2\beta }$
故 $f(\rho )=F(l+1-\frac{\alpha }{2\beta },2(l+1),\rho )$
从而 $R(r)=\frac{u(r)}{r}=\frac{r^{l+1}{e^{-\beta r}}}{r}f(\rho )={r^{l}}{e^{-\beta r}}F(l+1-\frac{\alpha }{2\beta },2(l+1),2\beta r)$
已知当 $x\to \infty$ 时, $F(a,c,x)\sim {e^{x}}$, 故 $\underset{r\to \infty }{\mathop{\lim }}\,R(r)=\underset{r\to \infty }{\mathop{\lim }}\,{r^{l}}{e^{-\beta r}}{e^{2\beta r}}=\underset{r\to \infty }{\mathop{\lim }}\,{r^{l}}{e^{\beta r}}\to \infty$
为保证波函数有限性必须将F截断为多项式, 只须
\[l+1-\frac{\alpha }{2\beta }=-{n_{r}},\ {n_{r}}\ge 0,\,\ F(l+1-\frac{\alpha }{2\beta },2(l+1),2\beta r){n_{r}}\]定义 $\frac{\alpha }{2\beta }=l+1+{n_{r}}\equiv n$ 为主量子数
\[n=\frac{\alpha }{2\beta }=\frac{2\mu \kappa Z{e^{2}}}{4\pi {\varepsilon_{0}}{\hbar^{2}}}\frac{1}{2\sqrt{\frac{-2\mu E}{\hbar^{2}}}}=\frac{\mu \kappa Z{e^{2}}}{4\pi {\varepsilon_{0}}\hbar \sqrt{-2\mu E}}\]从而能级为 $E_n=-\frac{1}{2}\frac{\mu {\kappa^{2}}{Z^{2}}{e^{4}}} { (4\pi \varepsilon_0)^{2} {\hbar^{2}} {n^2} }$
另, 也利用下面变换也可以化简方程, 但仍然无法直接求解, 只是形式显得简单一些
\[-\frac{1}{\rho^{2}}\frac{d}{d\rho }\left( {\rho^{2}}\frac{dR}{d\rho } \right)+\left[ \frac{l(l+1)}{\rho^{2}}+V(\rho ) \right]R(\rho )=ER(\rho ) \\x=\ln \rho ,\ y=\sqrt{\rho }R \\ {y}''=\gamma y={e^{2x}}(V-E)+{(l+\frac{1}{2})}^{2}\]径向部分解Laguerre函数
一般, 数学上定义广义Laguerre函数
\[L_{n}^{\alpha }(x)=\frac{e^{x} {x}^{-\alpha }}{n!} \frac{d^{n}}{d{x^{n}}}({e^{-x}}{x^{n+\alpha }})=\sum\limits_{i=0}^{n}{(-1)}^{i}\left( \begin{matrix} n+\alpha \\ n-i \\ \end{matrix} \right)\frac{x^{i}}{i!}=\sum\limits_{i=0}^{n}{(-1)^{i}}\frac{(n+\alpha )!}{(n-i)!(\alpha +i)!}\frac{x^{i}}{i!}\]满足如下微分方程
$x{y}’’+(\alpha +1-x){y}’+ny=0$
并有正交性
\[\int_{0}^{+\infty } {x}^{\alpha } {e^{-x}}L_{m}^{\alpha }(x)L_{n}^{\alpha }(x)dx=\frac{\Gamma (n+\alpha +1)}{n!}{\delta_{mn}}=\frac{(n+\alpha )!}{n!} {\delta_{mn}}\] \[\int_{0}^{+\infty } {x}^{\alpha +1} {e^{-x}} {\left[ L_{n}^{\alpha }(x) \right]}^{2}dx=\frac{(n+\alpha )!}{n!}(2n+\alpha +1)\]类氢波函数
$R(r)=\frac{u(r)}{r}=\frac{1}{r}{r^{l+1}}{e^{-\beta r}}f(r)={r^{l}}{e^{-\beta r}}f(r)$
\[\alpha =\frac{2Z}{a_{0}},{\beta^{2}}=-\frac{2\mu E}{\hbar^{2}},{a_{0}}=\frac{4\pi {\varepsilon_{0}}{\hbar^{2}}}{\mu {e^{2}}}\] \[r{f}''(r)+2(l+1-\beta r){f}'(r)+[\alpha -2\beta (l+1)]f(r)=0\]令 $\rho=2\beta r=\frac{2Z}{na_0}r, r=\frac{\rho}{2\beta}$, $\frac{\alpha}{2\beta}=n,2\beta=\frac{\alpha}{n}=\frac{2Z}{na_0},\beta=\frac{Z}{na_0}$
\[\begin{align} & \ \rho {f}''(\rho )+[2(l+1)-\rho )]{f}'(\rho )+[\frac{\alpha }{2\beta }-(l+1)]f(\rho )=0 \\ & \rho {f}''(\rho )+[2l+1+1-\rho )]{f}'(\rho )+[\frac{\alpha }{2\beta }-l-1]f(\rho )=0 \\ \end{align}\]$\rho {f}’’(\rho )+[2l+1+1-\rho )]{f}’(\rho )+[n-l-1]f(\rho )=0$
对比 $x{y}’’+(A+1-x){y}’+Ny=0$, 知 $A=2l+1,N=n-l-1$, 故
\[f(\rho )=L_{N}^{A}(\rho )=L_{n-l-1}^{2l+1}(\rho )\] \[R(r)={r^{l}}{e^{-\beta r}}f(\rho )={r^{l}}{e^{-\beta r}}L_{n-l-1}^{2l+1}(\rho )={\left( \frac{\rho }{2\beta } \right)}^{l} {e^{-\rho /2}}L_{n-l-1}^{2l+1}(\rho )=R(\rho )\]归一化要求
\[\begin{align} & \frac{1}{c^{2}}=\int_{0}^{+\infty }{r^{2}}{R^{2}}(r)dr=\int_{0}^{+\infty } {\left( \frac{\rho }{2\beta } \right)}^{2} {R^{2}}(\rho )\frac{d\rho }{2\beta } \\ & { (2\beta)^3 \over c^{2}}=\int_{0}^{+\infty} \rho^{2} {R^{2}}(\rho )d\rho =\int_{0}^{+\infty } \rho^{2} {(\frac{\rho }{2\beta })}^{2l} {e^{-\rho }} {\left[ L_{n-l-1}^{2l+1}(\rho ) \right]}^{2} d\rho \\ & { (2\beta)^{3+2l} \over c^{2}} =\int_{0}^{+\infty }{\rho^{2l+1+1}}{e^{-\rho }} {\left[ L_{n-l-1}^{2l+1}(\rho ) \right]}^{2}d\rho \end{align}\]对比 \(\int_{0}^{+\infty } {x}^{A+1} {e^{-x}} {\left[ L_{N}^{A}(x) \right]}^{2}dx=\frac{(N+A)!}{N!}(2N+A+1)\)
\[{ (2\beta)^{3+2l} \over c^2}=\int_{0}^{+\infty } {\rho^{2l+1+1}}{e^{-\rho }} {\left[ L_{n-l-1}^{2l+1}(\rho ) \right]}^{2} d\rho =\frac{(n+l)!}{\left( n-l-1 \right)!}2n\] \[{c^{2}}=\frac{\left( n-l-1 \right)!}{2n(n+l)!} {(2\beta )}^{3+2l}\]故
\[\begin{align} & R(r)=\sqrt{ \frac{\left( n-l-1 \right)!} {2n(n+l)!} {(2\beta )}^{3} } {(2\beta )}^{l} {r^{l}}{e^{-\beta r}}L_{n-l-1}^{2l+1}(2\beta r) \\ & =\sqrt{ \frac{\left( n-l-1 \right)!}{2n(n+l)!} {(\frac{2Z}{n{a_{0}}})}^{3} } {(\frac{2Z}{n{a_{0}}}r)}^{l} {e^{-\frac{Z}{n{a_{0}}}r}}L_{n-l-1}^{2l+1}(\frac{2Z}{n{a_{0}}}r) \end{align}\] \[R(\rho )=\sqrt{ \frac{\left( n-l-1 \right)!} {2n(n+l)!} {(\frac{2Z}{n{a_{0}}})}^{3} }{\rho }^{l} {e^{-\rho /2}}L_{n-l-1}^{2l+1}(\rho )\]以波尔 $a_0$ 作单位时
\[R(r^*)=\sqrt{ \frac{\left( n-l-1 \right)!} {2n(n+l)!} {(\frac{2Z}{n{a_{0}}})}^{3} } {(\frac{2Z}{n}r^*)}^{l} {e^{-\frac{Z}{n}r*}}L_{n-l-1}^{2l+1}(\frac{2Z}{n}r^*)\]EigenMath中可用如下脚本计算此函数
# Language: bash
n=1
l=0
sqrt( (n-l-1)!*(2*Za/n)^3/(2*n*(n+l)!) ) * rho^l * exp(-rho/2) * laguerre(rho,n-l-1,2*l+1)
径向函数部分可对照徐光宪和黎乐民所著的《量子化学基本原理和从头计算法》
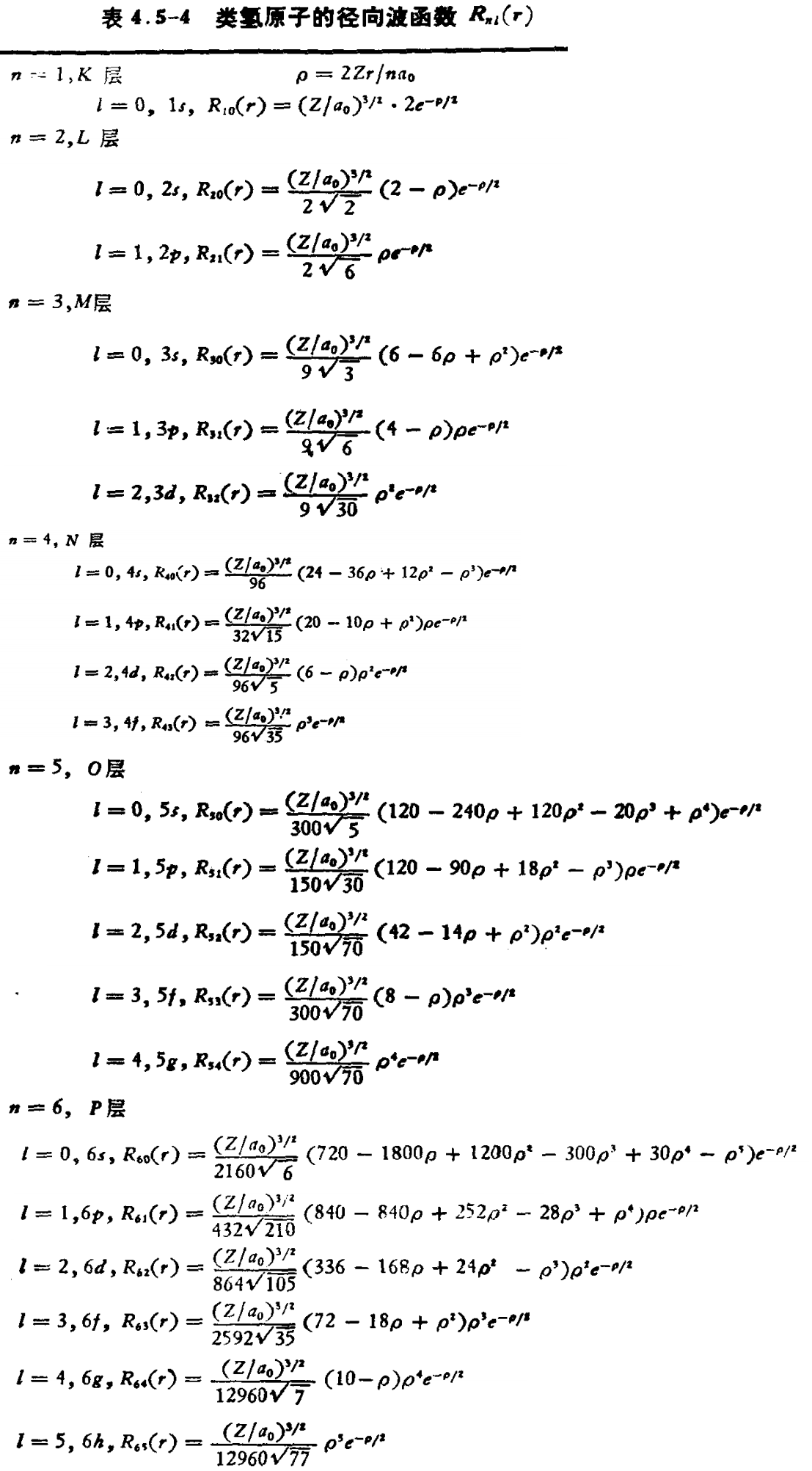
注意
-
有些化学书上所用Laguerre函数定义与数学上定义有区别, 因此所给出的公式不同, 但约化后两者一致.
-
化学中常用的 \(L_{n+l}^{2l+1}\) 实际相应于数学上的 \(n!L_{n-l-1}^{2l+1}\)
