哲●科●文Jerkwin 类别 标签 链接 关于 订阅

Martini实例教程：脂质

类别: 科   标签: gmx martini   阅读次数:   版权: (CC) BY-NC-SA ✕

脂质双分子层

Martini粗粒化模型一开始就是为脂质开发的[1, 2]. Martini方法的主要思想是, 根据简单的分子构建模块构建可扩展的粗粒化模型, 使用少量的参数和标准的相互作用势达到实用性与可移植性的最大化. Martini大致把全原子(重原子)按照4:1的比例转化为粗粒化珠子, 在2.0版本[2]中, 定义了18种珠子类型来表征其化学特性. 粗粒化珠子具有固定的大小, 相互之间通过相互作用映射进行作用, 映射具有10种不同的作用强度. 由于Martini的模块化, 人们对大量不同的脂质类型进行了参数化, 例如可以参看Martini脂质拓扑.

这些教程假定读者对Linux操作系统和GROMACS分子动力学的程序包有基本的了解. 这里有一份很好的Gromacs教程<md.chem.rug.nl/~mdcourse/>.

本教程的目的是建立磷脂双分子层的Martini粗粒化模型, 并研究其性质. 首先, 我们将尝试自发组装形成DSPC双分子层并查看表征磷脂层的各种不同的性质, 比如每个脂分子的面积, 双分子层的厚度, 序参量和扩散. 然后, 我们将改变脂质头基和尾端的特性, 并了解它们如何影响上述性质. 最后, 我们会继续前进, 建立更复杂的多组分双分子层.

下载本教程所需要的文件: bilayer_tutorial.zip. 解压lipid-tutorial.tar.gz文件(会得到名称为bilayer-tutorial的目录).

双层膜的自组装

我们将由模拟盒子中随机分布的脂质分子和水开始, 得到自组装的二硬脂酰-磷脂酰胆碱双分子层(DSPC). 进入spontaneous-assembly子目录. 首先, 根据单个DSPC分子的构型, 构建128个DSPC分子随机分布的构型:

genbox -ci dspc_single.gro -nmol 128 -box 7.5 7.5 7.5 -try 500 -o 128_noW.gro

接着对体系进行能量最小化…

grompp -f minimization.mdp -c 128_noW.gro -p dspc.top -maxwarn 10 -o dspc-min-init.tpr

mdrun -deffnm dspc-min-init -v -c 128_minimised.gro

…每个脂质分子添加6个粗粒度水分子(共24个全原子水)…

genbox -cp 128_minimised.gro -cs water.gro -o waterbox.gro -maxsol 768 -vdwd 0.21

-vdwd的值(默认范德华半径)必须从其默认原子长度(0.105 nm)增加到可以反应Martini粗粒化珠子大小的值.

…然后再次进行能量最小化(保证dspc.top里面的水珠子与增加到体系里面的相匹配):

grompp -f minimization.mdp -c waterbox.gro -p dspc.top -maxwarn 10 -o dspc-min-solvent.tpr

mdrun -deffnm dspc-min-solvent -v -c minimised.gro

现在, 你可以准备进行自组装的分子动力学模拟了, 大约运行25 ns就够了.

grompp -f martini_md.mdp -c minimised.gro -p dspc.top -maxwarn 10 -o dspc-md.tpr

mdrun -deffnm dspc-md -v

在单个CPU上完成上面的模拟大约需要45 min, 但mdrun默认会使用机器上所有可用的CPU. 你可以使用mdrun -nt选项来调整使用的并行线程数. 在最终模拟完成之前, 你可以随时检查模拟进程, 查看是否已经形成了双分子层. 最简单的方法是使用GROMACS自带的可视化软件:

ngmx -f dspc-md.xtc -s dspc-md.tpr

或者使用VMD. 开始和最后的结构应该与图1类似. 同时, 仔细查看Martini的参数文件, 特别是相互作用和珠子类型. PC与PE的头基, 饱和与不饱和的尾端之间有那些区别?

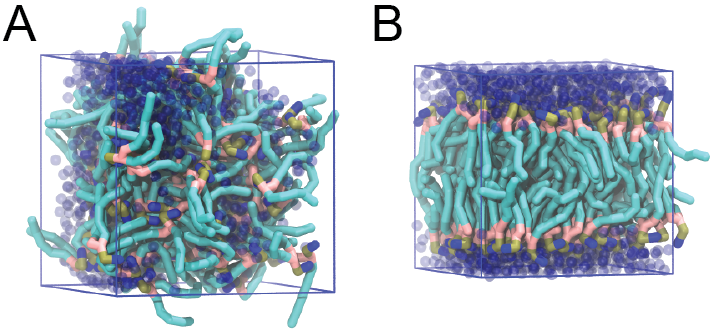
图1 DSPC双分子层的形成. A) 随机分布于水分子中的64个DSPC脂质分子. B) 30 ns模拟后, DSPC脂质分子已经聚合在一起形成了双分子层.

检查一下你是否得到了双分子层. 如果是, 检查一下所形成的膜是否垂直于Z轴(也就是膜处于XY平面内). 如果不垂直于Z轴, 可以对体系进行相应的旋转(使用editconf命令). 如果根本没有形成双分子层, 那就从已经形成双分子层的dspc_bilayer.gro开始继续. 在表面张力为0(使用半各向同性压力耦合), 温度为341 K的条件下开始另一个15 ns的模拟. 这个温度高于实验中DSPC的凝胶-液晶转变温度. 你可以在GROMACS手册中找到如何改变压强耦合与温度的说明: <manual.gromacs.org/current/online.html>. 同样的, 你可能不想一直等着这个模拟过程结束再查看最终结果. 在这种情况下, 你可以跳过此步, 使用spontaneous-assembly/allfiles/子目录中的轨迹继续下面的步骤.

双层膜的分析

对上面的模拟, 我们可以计算以下性质:

通常来说, 进行分析时, 你可能要舍弃模拟的前几ns, 将其作为平衡所需要的时间.

每个脂质分子的面积

为计算每个脂质分子的(投影)面积, 你可以简单地使用模拟盒子的面积(Box-X和Box-Y的乘积, 通过g_energy得到)除以体系中脂质分子数目的一半. (注意到这个方法并不严密, 因为在自组装形成的双层膜中, 每个单层所含的脂分子数目可能会有一些不对称性, 即对于两个单分子层来说, 每个脂质分子的面积是不同的. 然而, 作为粗略的近似, 我们可以忽略这些).

膜的厚度

可以使用g_density得到膜的厚度. 在使用g_density命令时, 可以通过提供合适的索引文件(利用make_index创建; 例如, 输入a P*, 可以获得磷酸盐珠子的索引)计算脂质分子中不同官能团的密度(比如, 磷酸盐和氨盐基的头基珠子, 尾端的碳珠子等). 根据密度分布曲线中头基峰之间的距离可以计算出膜的厚度.

与实验相比的更适合的做法是计算电子密度分布. g_density工具也提供了这一选项. 不过, 你需要提供一个数据文件, 其中包含每个珠子含有的电子数(-ei electrons.dat选项). GROMACS手册中介绍了该文件的格式.

将你得到的结果与小角中子散射实验得到的结果做对比[3]:

侧向扩散

在计算侧向扩散系数之前, 消除模拟过程中之, 珠子在盒子边界上的跳跃(trjconv -pbc nojump命令). 然后使用g_mad计算侧向扩散系数. 注意要移除整体的质心运动(-rmcomm【注】), 并只对均方位移曲线的线性区域进行线性拟合(使用g_msd的-beginfit和-endfit选项). 使用-lateral z选项, 得到侧向扩散系数.

为比较Martini模拟得到的扩散系数与实验测量值, 必须使用大约为4的转换系数, 以考虑粗粒化对自由能形貌进行平滑而导致的扩散加快(注意, 对不同的分子, 这个转换系数可能有显著区别).

【注】在GROMACS版本3中, 此选项不能用. 使用trjconv -center可解决这个问题.

序参量

现在我们要计算二阶序参量, 其定义为:

$P_2 = {1 \over 2} (3 <\cos^2 \q> -1)$

其中 $\q$ 为键与双分子层法向之间的夹角. $P_2=1$ 意味着键完全沿双分子层法向排列, $P_2=-0.5$ 表示反向排列, $P_2=0$ 表示无规则取向, 随机排列.

一个计算这些序参量的脚本可以在这里下载(scripts/目录下有另一个版本). 复制.xtc与.tpr文件到分析的子目录下(脚本默认它们的名字分别为traj.xtc和topol.tpr. 你可能要使用spontaneous-assembly/allfiles/目录下15 ns模拟的结果). 脚本do-order-multi.py会计算 $P_2$. 当运行时, 它需要一些参数. 例如, 命令:

./do-order-multi.py traj.xtc 0 15000 20 0 0 1 64 DSPC

会从轨迹文件traj.xtc中读取0-15 ns的构型进行计算. 模拟中含有64个DSPC脂质分子, 输出为相对于z轴的 $P_2$, 取等间距的轨迹构型, 每20帧平均一次.

其他分析

不同的科学问题需要不同的分析方法, 没有一种工具可以包含所有的分析方法. GROMACS软件包中有各种分析工具可用, 具体请参见GROMACS手册: <manual.gromacs.org/current/online.html>. 因此, 大部分模拟研究组都发展了一系列自己的脚本和程序, 它们大部分都可以免费获得, 比如形态图像分析和3D压力场工具可以在这里下载. 除此之外, 还有很多程序包可用来进行分析和发展你自己的工具, 比如python的MDAnalysis包https://pypi.python.org/pypi/MDAnalysis/.

改变脂质分子类型

脂质分子可以认为是模块化分子. 在这部分, 我们利用Martini模型研究脂质分子尾端以及头基的改变对双层膜性质的影响. 我们会 i) 在脂质分子尾端引入双键 ii) 将脂质分子的头基从磷脂酰胆碱(PC)更改为磷脂酰乙醇胺(PE).

不饱和尾端

为在尾端引入双键, 我们使用DOPC替代DSPC(根据Martini拓扑文件martini_v2.0_lipids.itp比较两种脂质分子的差别). 在.top与.mdp文件中将DSPC替换为DOPC, 然后grompp会帮你完成剩下的工作(你可以忽略grompp的警告atom name does not match)

改变头基

再次从DSPC模拟的最终构型开始, 将头基由PC改为PE. 对这两个新系统, 进行15 ns的MD模拟并比较三种双分子层(DSPC, DOPC, DSPE)以上性质(每个脂质分子的面积, 膜的厚度, 键的 $P_2$ 序参量, 脂质侧向扩散系数)的不同. 你观察到的变化与预期相符吗? 为什么? 讨论一下.

复合膜

当构建更大, 更复杂的双层膜时, 使用一个接近平衡的膜而不是让膜进行自组装, 会更加方便, 也是必要的. 这可以通过连接(比如使用editconf), 或者改变之前形成的膜, 或者使用成膜程序比如insane.py来完成, insane.py可以在scripts/目录下找到, 或从这里下载. INSANE(INSert membrANE)是一个粗粒化建模工具, 它通过将脂质分子分布在格点上来构建膜. 膜的结构源于简单的模板定义, 可以添加到程序中, 或者利用在命令行中指定的头基, 连接部分和脂质尾端进行组合. 这个程序使用两个格点, 分别用于双分子层的内侧和外侧, 然后将指定相对数量的脂质分子随机放在格点上. 这样就可以构建包含指定脂质成分的不对称的膜. 这个程序也可以添加溶剂和离子, 利用相似的格点方法将它们分布到3D的格点上. 关于INSANE功能的更多信息可以通过运行insane.py -h查看.

在complex-bilayers/目录下, 我们将使用insane.py构建完全水合, 由DPPC:DUPC:CHOL按照4:3:3的比例组成, 处于生理离子浓度下的膜. 这与Risselada和Marrink[4]用于展示阀形成时所用的膜类似. 开始运行INSANE:

./insane.py -l DPPC:4 -l DUPC:3 -l CHOL:3 -salt 0.15 -x 15 -y 10 -z 9 -d 0 -pbc cubic -sol W -o dppc-dupc-chol-insane.gro

这将为体系生成一个初始构型dppc-dupc-chol-insane.gro(图2A), 并提供.top文件的初始信息. 下一步, 修改.top文件使其包含正确的Martini拓扑. 然后, 对构型进行能量最小化并运行一个短时间(10 ns)的平衡模拟, 方法类似之前脂质分子自组装的模拟类似. 注意, 因为这次模拟包含了很多组分, 你必须(利用make_ndx)创建一个索引文件, 并将所有脂质分子, 所有溶剂分子分别放在不同的组中以对应.mdp文件中指定的组. 因为所有的脂质分子和溶剂都置于格点上(图2A), 所以即使能量最小化之后, 它们仍然可能处于能量不利的状态. 由于体系中的相互作用力很大, 所以在使用Martini脂质时间步长(30-40 fs)进行成品模拟之前, 使用小的时间步长(1-10 fs)进行平衡模拟很有必要. 由insane.py给出的初始格点顺序会在几ns的时间内得到松弛(图2B), 我们建议先使用Berendsen压力耦合算法进行5-30 ns的模拟以弛豫膜的面积, 然后使用Parrinello-Rahman压力耦合方法进行成品模拟. 这个复合膜在295 K会发生相分离, 但需要几微妙的时间(图2C).

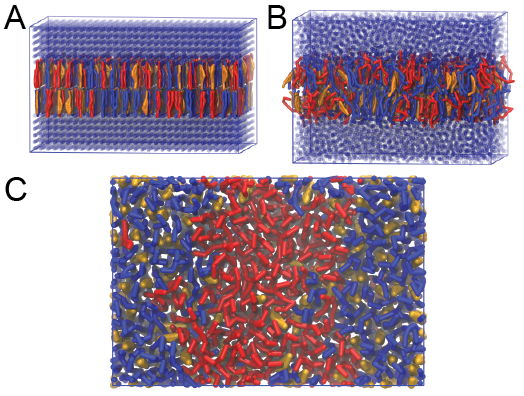
图2 DPPC-DUPC-CHOL双层膜的形成. A) 使用insane.py构建DPPC-DUPC-CHOL比例为4:3:3的膜. B) 经过20 ns的模拟之后, 格点结构消失, 膜的面积达到平衡. C) 295 K时, 复合膜相分离成为Ld和Lo, 这个相变过程需要几微秒, 图中显示了在6微秒之后的俯视图. 图中DPPC用红色, DUPC用蓝色, 胆固醇用红色来表示.

进阶: 无溶剂Martini和囊泡

在本教程中, 我们将要学习由于分层和Lo和Ld相的形成而导致的脂质囊泡变形. 为研究这种由大量粒子组成的体系, 最近发展了一种特定的力场: Dry Martini. 这个由Martini衍生出的力场, 正如其名字暗示的一样, 不需要任何水溶剂并且允许模拟更大的体系.

这种力场需要 使用非常特定的参数进行成品模拟, 所有解释都可以这个压缩包中找到.

  1. 利用martini_vesicle_builder.py脚本构建囊泡. 下面的命令会创建一个由DPPC, DUPC(DLiPC)和胆固醇分子随机分布形成的直径为25 nm的囊泡.

    python martini_vesicle_builder.py 12.5 DPPC:DUPC,60:40 43 1> system.gro 2> system.top

  2. 对体系进行能量最小化.
  3. 平衡体系. 在这种情况下, 需要平衡很长时间: 囊泡是以单纯平坦的膜的性质(厚度和每个脂质分子面积)为基础得到的, 由于囊泡双层的弯曲这些性质发生剧烈变化. 膜上会形成孔洞, 但它们会很快消失并且有助于囊泡的平衡(翻转).
  4. 成品模拟至少需要10 ns. 检查体系几何形状的变化: 分层是如何影响囊泡球形的? 图3给出了一个例子.

更新

我们建议你采用CHARMM-GUI来构建囊泡. 根据这里的教程学习如何使用CHARMM-GUI, 平衡好你的囊泡后继续按照上面的教程进行即可.

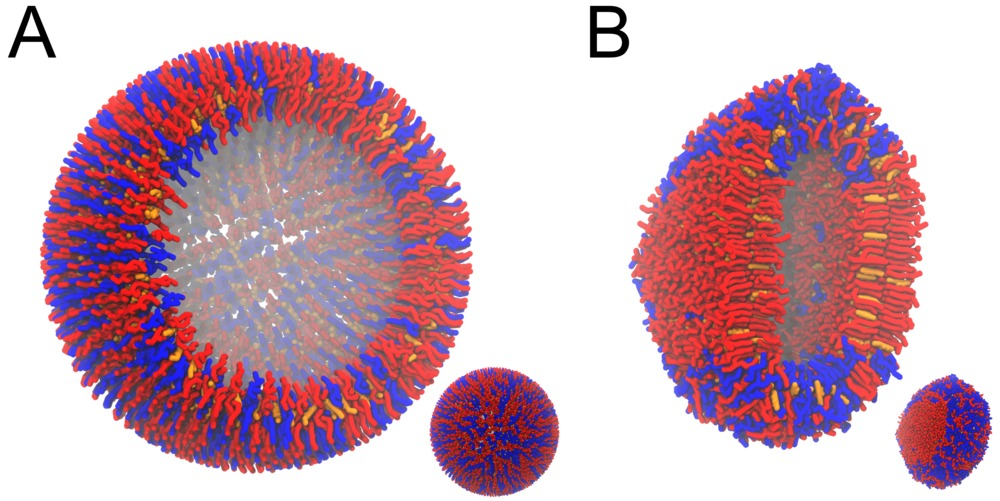
图3 DPPC-DUPC-CHOL组成的囊泡, 球形到圆环形的改变过程. A) 初始体系, B) 20 ns模拟之后的构型, 注意到囊泡平的一侧表示了Lo相(DPPC/CHOL). 插图表示整个系统, 大图表示切面图.

进阶: 改变脂质参数

警告: 这部分内容是好几年以前的了, 并且最近没有测试过. 此外, 这部分使用的细粒度-粗粒度(FG-CG)转换工具, 会在后面的Martini教程中给出. 如果你不熟悉这个工具, 可能要跳过这部分.

在这部分, 我们会试着改进diC18:2-PC分子的Martini参数, 它是一个有着两个不饱和尾端的PC脂质分子. 我们会优化Martini参数使得脂质分子尾端的二面角和键角分布与100 ns全原子模拟(全原子数据在fg.xtc中)的结果尽可能一致. 这部分所需要的文件在refin/目录中.

这个任务可以分为五步:

  1. 根据之前定义的映射规则【注】, 将全原子构型(FG)转换为相对应粗粒化构型.
  2. 计算键角和二面角分布. 这些将作为之后的参考(“黄金标准”).
  3. 对体系进行粗粒化的模拟.
  4. 计算键角和二面角分布, 并且与第二步的参考值作对比.
  5. 改变粗粒化参数, 重复3、4步直至得到满意的结果.

【注】映射规则已经定义好了, 具体查看dupc_fg.itp中的mapping部分.

要进行从FG到CG的转换, 我们可以使用g_fg2cg程序, 它是GROMACS修改版本的一部分, 你需要自己安装(参考逆转换教程)

source /GMX/安装路径/bin/GMXRC

setenv GMXLIB /GMX/安装路径/share/top

首先, 将FG转换为CG:

g_fg2cg -pfg fg.top -pcg cg.top -c fg.gro -n 1 -o cg.gro

g_fg2cg -pfg fg.top -pcg cg.top -c fg.xtc -n 1 -o fg2cg.xtc

然后, 创建一个脂质尾端的索引文件, 为计算键角和二面角分布作准备:

make_ndx -f cg.gro -o angle.ndx
aGL1 | aC1A | aD2A
aC1A | aD2A | aD3A
aD2A | aD3A | aC4A
aC1A | aD2A | aD3A | aC4A
q

现在利用g_angle计算分布:

g_angle -f fg2cg.xtc -type angle -n angle.ndx -od fg2cg ang{1,2,3}.xvg

g_angle -f fg2cg.xtc -type dihedral -n angle.ndx -od fg2cg dih1.xvg

这些就是我们想要利用CG模型得到的角度分布的目标值. 作为初始值, 我们使用在duoc_cg.itp中已经定义好的Martini参数, 即所有角度都是180°. 进行一个短时间的粗粒化模拟(从cg_mdstart.gro开始, 只需要在cg.top中添加水分子). (不要忘了source GROMACS的正常版本!) 你需要创建一个合适的.mdp文件. 注意到FG轨迹是在300 K温度下得到的. 将键角和二面角分布与g_fg2cg参考值对比之后, 改变dupc_cg.itp中的角度参数并重复上面的步骤.

本教程所用的工具和脚本

参考文献

1. Marrink, S. J., De Vries, A. H., and Mark, A. E. (2004) Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B 108, 750-760.

2. Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., and De Vries, A. H. (2007) The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 111, 7812-7824.

3. Balgavy, P., Dubnicková, M., Kucerka, N., Kiselev, M. A., Yaradaikin, S. P., and Uhrikova, D. (2001) Bilayer thickness and lipid interface area in unilamellar extruded 1,2-diacylphosphatidylcholine liposomes: a small-angle neutron scattering study. Biochim. Biophys. Acta 1512, 40-52.

4. Risselada, H. J., and Marrink, S. J. (2008) The molecular face of lipid rafts in model membranes. Proc. Natl. Acad. Sci. U.S.A. 105, 17367-17372.

◆本文地址: , 转载请注明◆
◆评论问题: https://jerkwin.herokuapp.com/category/3/博客, 欢迎留言◆
前一篇:　远程服务器映射软件ExpanDrive中文版
后一篇:　单位换算器
访问人次(2015年7月 9日起): | 最后更新: 2024-04-16 06:38:20 UTC | 版权所有 © 2008 - 2024 Jerkwin 个