- 2019-02-08 17:35:38
以前的时候讲过如何使用gnuplot拟合颜色映射解析表达式, 在拟合时使用了分段三次函数. 如果要处理的拟合数据不多, 分段的范围可以手动指定, 虽然显得很笨拙. 如果要拟合大量的数据, 那就需要自动处理, 手动指定拟合范围就不实际了. 最近需要拟合很多的数据, 就重新思考了一下这个问题, 完成了拟合需要的gnuplot脚本.
问题
给出一系列n个数据点, (x_i, y_i), i=1..n, 求y在整个x范围内的分段解析表达式.
解析表达式可以自定义, 一般可以使用多项式.
要求自动确定分段节点. 节点的选择标准是所得解析表达式在两个相邻节点间的平均误差不超过指定值.
得到的解析表达式可用于不方便使用查表或内插的情况. 如果给定的解析表达式是三次函数, 得到的节点可作为三次样条的节点.
算法
读入数据(x_i, y_i), i=1..n, 将x_1作为第一个节点, x_n作为第二个节点, 拟合, 计算平均拟合误差.
如果平均拟合误差大于指定值, 说明选区的范围过大, 需要减小范围. 因此将x_n的前一个点x_n-1作为新的节点, 重新拟合, 计算平均拟合误差.
重复上面的步骤, 直至所得平均拟合误差满足要求, 得到两个节点x_1, x_k.
将x_k作为新的第一个节点, 重复以上步骤, 直至所有x值都处理完毕.
之所以选择从使用x值反向递减的拟合策略, 而不使用x值正向递增的拟合粗略, 是为了得到的节点范围尽量大, 这样所得的分段函数使用更方便. 但这种策略的一个缺点在于无法准确地找到那些明显的不连续点.
代码
使用gnuplot自带的非线性拟合功能即可完成. 但鉴于这个过程中需要多次拟合循环, 而且要记录每次循环得到的节点, 所以需要使用数组功能. 只有gnuplot 5.2以上的版本才支持数组, 所以下面的代码不适用于低版本的gnuplot. 当然, 如果你非要将它用于低版本的gnuplot, 那你肯定能想到办法.
| cmfit.gpl | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 | # 载入数据集
load 'C:\Users\Jicun\Dropbox\!Script\gpl_cm.dat'
# 定义用到的拟合函数, 绘图函数
f(x)=a0+a1*x+a2*x**2+a3*x**3
F(x, beg, end, a0, a1, a2, a3)= beg<=x ? (x<end?a0+a1*x+a2*x**2+a3*x**3:1/0) : 1/0
set fit quiet # 屏幕不输出拟合过程
Nord=3 # 拟合阶数, 取决于所用拟合函数
maxSTD=1E-3 # 最大平均拟合偏差
col=2 # 要拟合的数据列
#cm='rainbow' # 使用的数据集
#cm='darkrainbow'
#cm='cetr2'
cm='viridis';
#cm='bgy'
#cm='parula'
#cm='avocado'
#cm='moreland';
#cm='thermometer'
#cm='redbluetones'
#cm='tmap'
#cm='ltmap'
#cm='cividis';
data = '$' . cm
# 不同数据集使用的数据点数, 间距可能不同
if(cm eq 'parula' \
|| cm eq 'viridis' \
|| cm eq 'moreland') { N=1024; dt=1./(N-1); dx=1.; nev=30 }
if(cm eq 'cividis' \
|| cm eq 'cetr2' \
|| cm eq 'rainbow' \
|| cm eq 'darkrainbow' \
|| cm eq 'avocado' \
|| cm eq 'bgy' \
|| cm eq 'thermometer' \
|| cm eq 'redbluetones' \
|| cm eq 'tmap' \
|| cm eq 'ltmap') { N=256; dt=1./(N-1); dx=dt; nev=10 }
# 以下为所得拟合结果
set tit cm
set xl"x"
set yl "RGB"
#plot [] [0:1] $rainbow \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.062745, 0.471375, -2.554017, -0.603914, 7.812982), \
F(x, 0.062745, 0.152941, 0.292460, 1.809704, -31.728520, 117.994977), \
F(x, 0.152941, 0.615686, 0.321657, -1.002195, 3.507752, -1.465506), \
F(x, 0.615686, 0.807843, 1.060710, -5.522637, 12.504767, -7.328945), \
F(x, 0.807843, 0.933333, 0.431446, -0.873251, 4.037986, -2.774247), \
F(x, 0.933333, 1.000000, 5.221261, -12.772499, 12.792531, -4.383959), \
F(x, 0.000000, 0.062745, 0.108729, 0.152568, -0.600651, 7.770915), \
F(x, 0.062745, 0.176471, 0.019507, 1.603318, -1.113349, 12.925571), \
F(x, 0.176471, 0.364706, -0.087439, 2.477820, 0.408927, -4.700034), \
F(x, 0.364706, 0.705882, 0.144965, 1.791961, -0.862001, -0.770124), \
F(x, 0.705882, 0.784314, 16.562714, -66.930100, 95.145955, -45.549403), \
F(x, 0.784314, 0.878431, -44.677970, 163.297275, -194.114854, 75.927463), \
F(x, 0.878431, 1.000000, 2.436863, -1.845566, -0.624881, 0.164628), \
F(x, 0.000000, 0.105882, 0.526474, 2.243463, 0.792247, -31.571500), \
F(x, 0.105882, 0.184314, 0.026914, 13.337161, -80.796176, 171.577097), \
F(x, 0.184314, 0.254902, 0.913699, -1.400599, 7.239935, -13.759153), \
F(x, 0.254902, 0.556863, 0.442544, 4.247120, -14.052824, 11.110080), \
F(x, 0.556863, 0.952941, 2.960527, -9.677238, 11.755653, -4.927506), \
F(x, 0.952941, 1.000000, 0.585773, -0.453645, 0.000000, -0.000000); exit
#plot [] [0:1] $darkrainbow \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.309804, 0.236537, 0.246053, -1.136582, 3.202751), \
F(x, 0.309804, 0.407843, -1.510327, 13.561592, -35.298055, 33.624234), \
F(x, 0.407843, 0.603922, -0.599178, 2.859926, -0.741459, -0.178725), \
F(x, 0.603922, 0.701961, 3.197059, -12.278383, 20.066775, -10.373348), \
F(x, 0.701961, 0.901961, 0.468624, 2.127260, -2.783342, 0.824166), \
F(x, 0.901961, 1.000000, 0.729870, 0.000000, -0.000000, 0.000000), \
F(x, 0.000000, 0.109804, 0.339471, 0.168823, -3.598735, 26.873972), \
F(x, 0.109804, 0.309804, 0.218689, 1.512175, -3.197075, 3.440555), \
F(x, 0.309804, 0.458824, -0.261191, 5.401505, -14.030694, 14.113778), \
F(x, 0.458824, 0.603922, -1.534715, 10.091878, -15.985773, 9.257180), \
F(x, 0.603922, 0.701961, 4.759391, -17.980549, 27.364646, -14.145868), \
F(x, 0.701961, 0.815686, 18.275342, -66.730000, 86.570221, -38.633344), \
F(x, 0.815686, 0.901961, -19.096521, 74.250435, -90.514567, 35.431661), \
F(x, 0.901961, 1.000000, 0.239399, 0.000000, -0.000000, 0.000000), \
F(x, 0.000000, 0.101961, 0.575370, -0.214218, 1.381410, -10.814899), \
F(x, 0.101961, 0.239216, 0.620844, 0.637717, -16.547215, 37.635934), \
F(x, 0.239216, 0.329412, -1.404892, 21.875973, -87.291389, 110.089969), \
F(x, 0.329412, 0.443137, -1.127449, 12.499131, -36.589253, 34.785129), \
F(x, 0.443137, 0.717647, 0.971421, -4.438096, 8.640928, -5.173692), \
F(x, 0.717647, 0.847059, 12.089098, -46.895840, 62.535294, -27.917903), \
F(x, 0.847059, 0.929412, -64.437519, 225.686918, -261.540385, 100.686232), \
F(x, 0.929412, 1.000000, 0.230961, 0.000000, -0.000000, 0.000000); exit
#plot [] [0:1] $cetr2 \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.137255, -0.000316, 0.038887, -0.883031, 5.101004), \
F(x, 0.137255, 0.203922, -4.023305, 61.355168, -303.724536, 513.861584), \
F(x, 0.203922, 0.305882, -1.622921, 20.396258, -74.241922, 90.162344), \
F(x, 0.305882, 0.396078, 8.471779, -73.154898, 211.089180, -195.491355), \
F(x, 0.396078, 0.623529, -0.543610, 2.677936, -0.137169, -0.445552), \
F(x, 0.623529, 0.749020, -15.225713, 68.550324, -96.645216, 45.458704), \
F(x, 0.749020, 1.000000, 2.274626, -4.643168, 5.626198, -2.267654), \
F(x, 0.000000, 0.207843, 0.204965, 2.709276, -7.313826, 9.194078), \
F(x, 0.207843, 0.396078, 0.376606, 0.109729, 4.680670, -7.355355), \
F(x, 0.396078, 0.619608, 0.865401, -1.956191, 5.447395, -3.937938), \
F(x, 0.619608, 0.760784, -8.802577, 42.865907, -62.175709, 29.088263), \
F(x, 0.760784, 0.992157, 7.266933, -22.020637, 25.525012, -10.575381), \
F(x, 0.992157, 1.000000, -17.632920, 38.955075, -21.133125, 0.000000), \
F(x, 0.000000, 0.203922, 0.963162, -2.861736, 0.251083, 4.557713), \
F(x, 0.203922, 0.313725, 0.656233, 0.043612, -5.790983, 0.106573), \
F(x, 0.313725, 0.400000, 17.430800, -140.294221, 376.158694, -334.690862), \
F(x, 0.400000, 0.631373, 0.328764, -2.247241, 5.614561, -3.859553), \
F(x, 0.631373, 0.968627, -0.646066, 4.007488, -5.858817, 2.485090), \
F(x, 0.968627, 1.000000, -0.000000, 0.000000, -0.000000, 0.000000); exit
plot [] [0:1] $viridis \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.455523, 0.282113, 0.585552, -3.199668, 3.273305), \
F(x, 0.455523, 0.700880, -2.797136, 18.565436, -37.531934, 24.521874), \
F(x, 0.700880, 1.000000, 4.563142, -18.410284, 23.559766, -8.759172), \
F(x, 0.000000, 0.074291, -0.000438, -0.351490, 48.354922, -360.945985), \
F(x, 0.074291, 0.702835, -0.014997, 1.564580, -1.154700, 0.700928), \
F(x, 0.702835, 1.000000, -0.960756, 4.427797, -3.482215, 0.926468), \
F(x, 0.000000, 0.476051, 0.327782, 1.734561, -4.300750, 3.500006), \
F(x, 0.476051, 0.932551, 0.218208, 1.243982, -0.736753, -0.849211), \
F(x, 0.932551, 1.000000, 348.076269, -1047.336499, 1048.282355, -348.910600); exit
#plot [] [0:1] $parula \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.115347, 0.209319, 0.021835, 8.049552, -184.003036), \
F(x, 0.115347, 0.184751, 2.374031, -44.761896, 276.704512, -556.160051), \
F(x, 0.184751, 0.317693, -0.399346, 3.459321, -4.534020, -6.611694), \
F(x, 0.317693, 0.447703, -2.173981, 20.360889, -61.942289, 62.029278), \
F(x, 0.447703, 0.675464, 4.243855, -25.971352, 50.451225, -29.381695), \
F(x, 0.675464, 0.840665, 1.758620, -8.829890, 15.820527, -7.604765), \
F(x, 0.840665, 1.000000, -47.324025, 160.987718, -178.222332, 65.537864), \
F(x, 0.000000, 0.122190, 0.166515, 1.467473, -0.294203, 23.661735), \
F(x, 0.122190, 0.328446, 0.142739, 2.829204, -8.770193, 13.750274), \
F(x, 0.328446, 0.695015, 0.308801, 0.881104, 0.574870, -1.368778), \
F(x, 0.695015, 0.842620, -14.989531, 63.658741, -85.592272, 38.217482), \
F(x, 0.842620, 1.000000, -14.773917, 50.485538, -55.874747, 21.147001), \
F(x, 0.000000, 0.109482, 0.530296, 2.857383, 6.806557, -41.144233), \
F(x, 0.109482, 0.232649, 0.465835, 7.313556, -40.797955, 70.197547), \
F(x, 0.232649, 0.384164, 1.953887, -11.423272, 39.003550, -44.999622), \
F(x, 0.384164, 0.675464, -0.247051, 7.832808, -17.887612, 11.458347), \
F(x, 0.675464, 0.862170, 9.308603, -35.135626, 47.027607, -21.482656), \
F(x, 0.862170, 1.000000, 14.096229, -43.850498, 47.004022, -17.195887); exit
#plot [] [0:1] $bgy \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.250980, 0.121646, -0.172462, -1.127437, 5.431302), \
F(x, 0.250980, 0.392157, -0.131357, 2.516024, -9.597266, 12.395703), \
F(x, 0.392157, 0.556863, -1.492039, 10.422082, -22.967599, 17.609067), \
F(x, 0.556863, 0.713725, -5.895145, 28.778858, -46.038523, 25.322913), \
F(x, 0.713725, 0.847059, -8.586891, 32.582707, -40.596624, 17.627591), \
F(x, 0.847059, 1.000000, -1.142666, 2.057658, -0.000297, 0.000113), \
F(x, 0.000000, 0.250980, 0.009478, 1.567212, 1.134523, -5.465413), \
F(x, 0.250980, 0.392157, 0.263542, -1.131873, 9.632994, -12.442064), \
F(x, 0.392157, 0.592157, 0.200958, 0.462406, 1.933537, -2.125990), \
F(x, 0.592157, 1.000000, -0.091472, 2.264930, -1.894472, 0.618395), \
F(x, 0.000000, 0.188235, 0.399324, 0.574092, 1.663684, -7.302784), \
F(x, 0.188235, 0.407843, 0.584562, -1.180634, 5.786781, -7.789910), \
F(x, 0.407843, 1.000000, 0.380303, 1.004679, -1.825543, 0.793271); exit
#plot [] [0:1] $avocado \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.254902, -0.000315, 0.019821, -0.238792, 0.738267), \
F(x, 0.254902, 0.521569, -0.384667, 1.975454, -2.290351, 2.092677), \
F(x, 0.521569, 0.784314, 0.251672, -2.065961, 5.852542, -3.112441), \
F(x, 0.784314, 1.000000, -0.264265, 1.264787, -0.000831, 0.000310), \
F(x, 0.000000, 0.258824, 0.000502, 1.740189, 0.372609, -1.140405), \
F(x, 0.258824, 0.521569, 0.294585, 0.168953, 2.224051, -2.019746), \
F(x, 0.521569, 1.000000, 0.427054, 0.465070, 0.118419, -0.025793), \
F(x, 0.000000, 0.407843, -0.000319, 0.297254, 0.186624, -0.857099), \
F(x, 0.407843, 0.886275, -0.121618, 1.027933, -1.611968, 0.962846), \
F(x, 0.886275, 1.000000, -0.107974, 0.338385, 0.000000, -0.000000); exit
#plot [:1] [0:1] $moreland \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.616813, 0.337271, 0.983489, 0.747265, -1.195076), \
F(x, 0.616813, 1.000000, -0.632934, 5.066503, -4.609700, 0.870305), \
F(x, 0.000000, 0.522972, 0.283621, 1.787108, -0.273675, -1.969690), \
F(x, 0.522972, 0.953079, 0.509720, 2.032810, -2.808791, 0.356746), \
F(x, 0.953079, 1.000000, 1127.813666, -3504.201247, 3632.816785, -1256.425801), \
F(x, 0.000000, 0.577713, 0.753360, 1.710547, -2.941316, -0.067188), \
F(x, 0.577713, 1.000000, 1.240366, 0.386625, -3.038613, 1.566723); exit
#plot [] [0:1] $thermometer \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.125490, 0.162174, 1.201690, -6.399066, 51.243518), \
F(x, 0.125490, 0.431373, 0.148005, 0.893940, 4.075881, -6.121149), \
F(x, 0.431373, 0.549020, -4.033245, 27.676482, -53.245771, 34.957323), \
F(x, 0.549020, 0.682353, 6.764309, -30.526849, 52.649881, -30.087859), \
F(x, 0.682353, 0.823529, -9.803570, 42.258774, -54.801709, 23.209690), \
F(x, 0.823529, 0.964706, 11.780482, -36.707047, 42.042428, -16.601556), \
F(x, 0.964706, 1.000000, 2.266182, -1.864046, 0.199584, -0.067639), \
F(x, 0.000000, 0.149020, 0.120337, 2.121807, -1.069806, 14.995654), \
F(x, 0.149020, 0.274510, -0.223638, 7.153696, -21.865513, 31.179040), \
F(x, 0.274510, 0.372549, 1.546500, -9.998720, 36.221021, -38.417792), \
F(x, 0.372549, 0.466667, 4.898614, -30.601930, 76.109977, -61.896098), \
F(x, 0.466667, 0.576471, 10.130934, -54.795573, 108.692312, -72.115484), \
F(x, 0.576471, 0.670588, 15.937621, -74.007429, 122.359430, -68.317410), \
F(x, 0.670588, 0.776471, 4.301756, -14.376467, 21.324263, -11.667634), \
F(x, 0.776471, 0.960784, -11.106730, 45.205518, -56.022964, 22.036255), \
F(x, 0.960784, 1.000000, 1.807516, -1.709471, -0.019174, 0.006442), \
F(x, 0.000000, 0.133333, 0.794128, 0.966570, 4.388059, -37.453981), \
F(x, 0.133333, 0.286275, 0.720815, 2.417972, -8.750889, 10.817765), \
F(x, 0.286275, 0.419608, 1.358732, -3.883291, 12.716874, -14.600037), \
F(x, 0.419608, 1.000000, 0.636442, 2.380296, -5.193566, 2.345535); exit
#plot [] [0:1] $redbluetones \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.274510, 0.449268, 1.574639, -0.822878, -1.491296), \
F(x, 0.274510, 0.403922, -0.288228, 8.474660, -22.200837, 20.561929), \
F(x, 0.403922, 0.509804, 3.707488, -19.016191, 42.456321, -31.670207), \
F(x, 0.509804, 0.635294, 9.680930, -46.704589, 83.339750, -50.422752), \
F(x, 0.635294, 0.878431, -2.137951, 13.824286, -20.185904, 8.656232), \
F(x, 0.878431, 1.000000, 34.681746, -106.281568, 110.295455, -38.557173), \
F(x, 0.000000, 0.113725, 0.156994, 1.203165, -4.497128, 33.013271), \
F(x, 0.113725, 0.321569, 0.143463, 0.889417, 4.005165, -5.745487), \
F(x, 0.321569, 0.435294, 2.876165, -21.447213, 64.655291, -60.582508), \
F(x, 0.435294, 0.529412, 10.474115, -64.301217, 140.750865, -101.324183), \
F(x, 0.529412, 0.635294, 11.899055, -59.479146, 106.631277, -63.671925), \
F(x, 0.635294, 0.752941, 3.869591, -13.953571, 22.184265, -12.226311), \
F(x, 0.752941, 0.905882, -7.963197, 32.488971, -39.126611, 15.003588), \
F(x, 0.905882, 1.000000, 2.422365, -2.104851, -0.009003, 0.003156), \
F(x, 0.000000, 0.184314, 0.219042, 0.690306, 0.608545, 2.946494), \
F(x, 0.184314, 0.529412, 0.260646, 0.314043, 2.383175, -2.250743), \
F(x, 0.529412, 0.639216, 8.263630, -42.062465, 77.213158, -46.359035), \
F(x, 0.639216, 0.741176, 11.232975, -48.568134, 75.137634, -38.554181), \
F(x, 0.741176, 0.850980, 4.206315, -14.675529, 21.410637, -10.502424), \
F(x, 0.850980, 0.929412, 72.226097, -246.169093, 283.448543, -109.133180), \
F(x, 0.929412, 1.000000, 2.153883, -1.589228, -0.021327, 0.007324); exit
#plot [] [0:1] $tmap \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.184314, 0.178983, 1.552415, -0.207975, 5.223602), \
F(x, 0.184314, 0.341176, 0.066012, 2.264477, 0.673474, -2.095856), \
F(x, 0.341176, 0.447059, 4.749953, -33.884109, 94.216232, -83.714029), \
F(x, 0.447059, 0.670588, -0.868992, 8.918165, -14.178095, 7.483969), \
F(x, 0.670588, 1.000000, -0.109994, 4.838318, -6.513456, 2.604411), \
F(x, 0.000000, 0.184314, 0.303925, 1.772992, -2.122434, 6.139617), \
F(x, 0.184314, 0.349020, 0.277610, 1.481387, 2.270264, -4.510611), \
F(x, 0.349020, 0.450980, 4.078043, -27.598191, 76.434953, -67.732938), \
F(x, 0.450980, 0.666667, -0.655808, 8.086928, -13.137827, 7.055502), \
F(x, 0.666667, 0.756863, 17.528872, -67.906478, 94.487329, -44.770083), \
F(x, 0.756863, 0.921569, 4.773772, -10.130974, 9.493433, -3.915789), \
F(x, 0.921569, 1.000000, 3.920833, -3.780528, -0.009403, 0.003226), \
F(x, 0.000000, 0.419608, 0.935393, 0.005125, 0.678124, -0.845400), \
F(x, 0.419608, 0.505882, 6.416300, -34.137703, 72.988688, -53.484807), \
F(x, 0.505882, 0.588235, 11.099459, -52.804586, 93.846613, -57.963352), \
F(x, 0.588235, 0.666667, 2.844359, -3.625769, -0.006251, 0.003290), \
F(x, 0.666667, 0.752941, -6.371378, 32.213485, -48.309479, 22.921856), \
F(x, 0.752941, 1.000000, 1.358718, -2.895860, 2.697215, -0.996030); exit
#plot [] [0:1] $ltmap \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.533333, 0.163818, 1.791632, -0.273066, -0.474513), \
F(x, 0.533333, 0.568627, 132.161025, -731.752508, 1358.253910, -838.937696), \
F(x, 0.568627, 1.000000, 0.374538, 2.632874, -3.441293, 1.279874), \
F(x, 0.000000, 0.121569, 0.283064, 2.509624, 3.097213, -20.814460), \
F(x, 0.121569, 0.262745, 0.526602, -1.130885, 18.376538, -36.628242), \
F(x, 0.262745, 0.368627, 1.975347, -13.981096, 52.456257, -59.971000), \
F(x, 0.368627, 0.482353, 4.081605, -24.751935, 63.659714, -53.109146), \
F(x, 0.482353, 0.607843, 3.013910, -12.490787, 25.671804, -17.528325), \
F(x, 0.607843, 0.698039, 22.796447, -103.139979, 163.020009, -86.219083), \
F(x, 0.698039, 0.815686, 21.113658, -80.795116, 108.914800, -49.613536), \
F(x, 0.815686, 0.933333, 21.071994, -69.419374, 80.770813, -32.128173), \
F(x, 0.933333, 1.000000, 2.643322, -2.266569, -0.011028, 0.003803), \
F(x, 0.000000, 0.450980, 0.936797, 0.075986, 0.411047, -0.704823), \
F(x, 0.450980, 0.909804, 1.411502, -0.307129, -1.841263, 0.895902), \
F(x, 0.909804, 1.000000, 1.269224, -1.085101, 0.010742, -0.003716); exit
#plot [0.:] [0.:1.1] $cividis \
u ($1*dx):2 ev nev w p pt 7 ps 2 lc 'red' , \
'' u ($1*dx):3 ev nev w p pt 7 ps 2 lc 'green', \
'' u ($1*dx):4 ev nev w p pt 7 ps 2 lc 'blue' , \
F(x, 0.000000, 0.121569, -0.000426, 0.060312, -1.553906, 10.160156), \
F(x, 0.121569, 0.196078, -1.982815, 32.605251, -172.417296, 319.227164), \
F(x, 0.196078, 0.666667, -0.133935, 2.107203, -2.734498, 2.026416), \
F(x, 0.666667, 0.988235, 0.321580, -0.218041, 1.387263, -0.470313), \
F(x, 0.988235, 1.000000, 1.000001, -0.000002, 0.000002, -0.000001), \
F(x, 0.000000, 1.000000, 0.125938, 0.709731, -0.053306, 0.135030), \
F(x, 0.000000, 0.078431, 0.302000, 1.452622, 8.254845, -63.440633), \
F(x, 0.078431, 0.509804, 0.463205, -0.353857, 0.722687, 0.040738), \
F(x, 0.509804, 0.976471, 0.546672, -0.581206, 1.466601, -1.184898), \
F(x, 0.976471, 0.992157,-6481.511854,19864.890017,-20291.986582, 6908.908418), \
F(x, 0.992157, 1.000000, 15.165100, -31.148250, 16.256250, 0.000000); exit
# 拟合代码
array Beg[N]; array End[N];
array A0[N]; array A1[N]; array A2[N]; array A3[N];
n=1; idx=1
while(n<N) {
beg=(n-1)*dt
i=N; FIT_STDFIT=1E99
if(N-n<Nord) {
a0=1; a1=0; a2=0; a3=0;
if(N-n==0){ fit [beg:1] f(x) data u ($1*dx):col via a0 }
if(N-n==1){ a1=1; fit [beg:1] f(x) data u ($1*dx):col via a0,a1 }
if(N-n==2){ a1=1; a2=1; fit [beg:1] f(x) data u ($1*dx):col via a0,a1,a2 }
Beg[idx]=beg; End[idx]=1; FIT_STDFIT=0
A0[idx]=a0; A1[idx]=a1; A2[idx]=a2; A3[idx]=a3
}
while(i>n && FIT_STDFIT>maxSTD) {
end=(i-1)*dt
a0=1; a1=1; a2=1; a3=1;
fit [beg:end] f(x) data u ($1*dx):col via a0,a1,a2,a3
print ">>>> ", n, i, i-n, beg, end, FIT_STDFIT
if(FIT_STDFIT<maxSTD || i-n==Nord) {
FIT_STDFIT=0
Beg[idx]=beg; End[idx]=end
A0[idx]=a0; A1[idx]=a1; A2[idx]=a2; A3[idx]=a3
} else {
i=i-1
}
}
n=i
idx=idx+1
}
# 输出拟合结果
do for [i=1:idx] {
print sprintf("F(x, %13.6f,%13.6f,%13.6f,%13.6f,%13.6f,%13.6f)", \
Beg[i], End[i], A0[i], A1[i], A2[i], A3[i])
} |
示例
python常用的viridis颜色映射来说吧, 原始数据和拟合结果对比如下
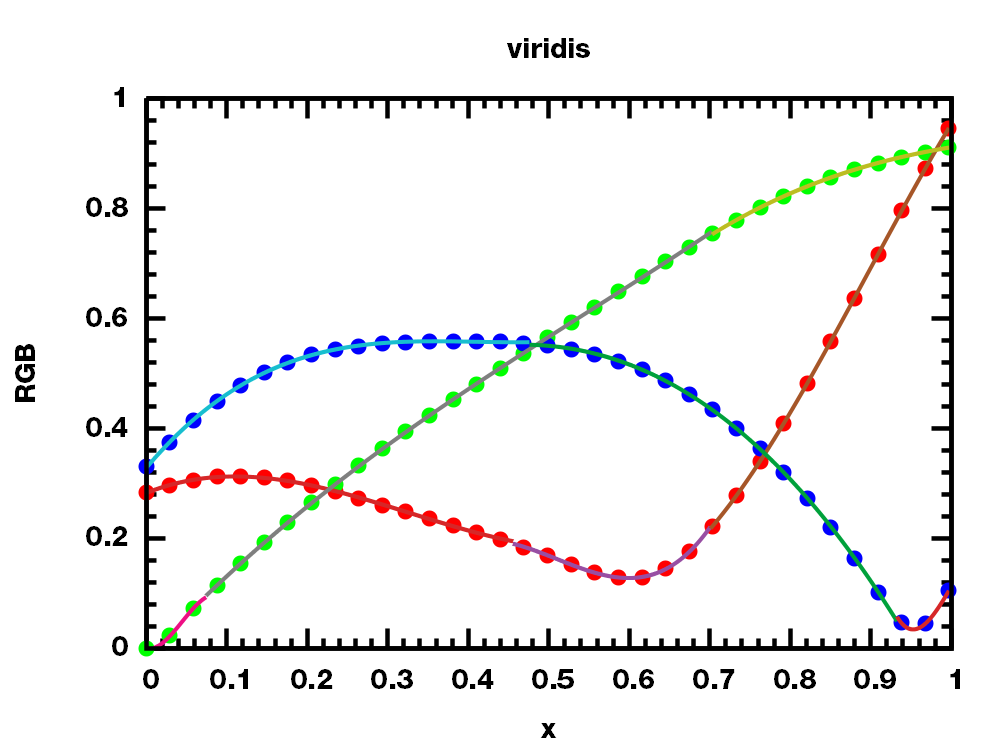
常见映射方案的颜色标尺如下
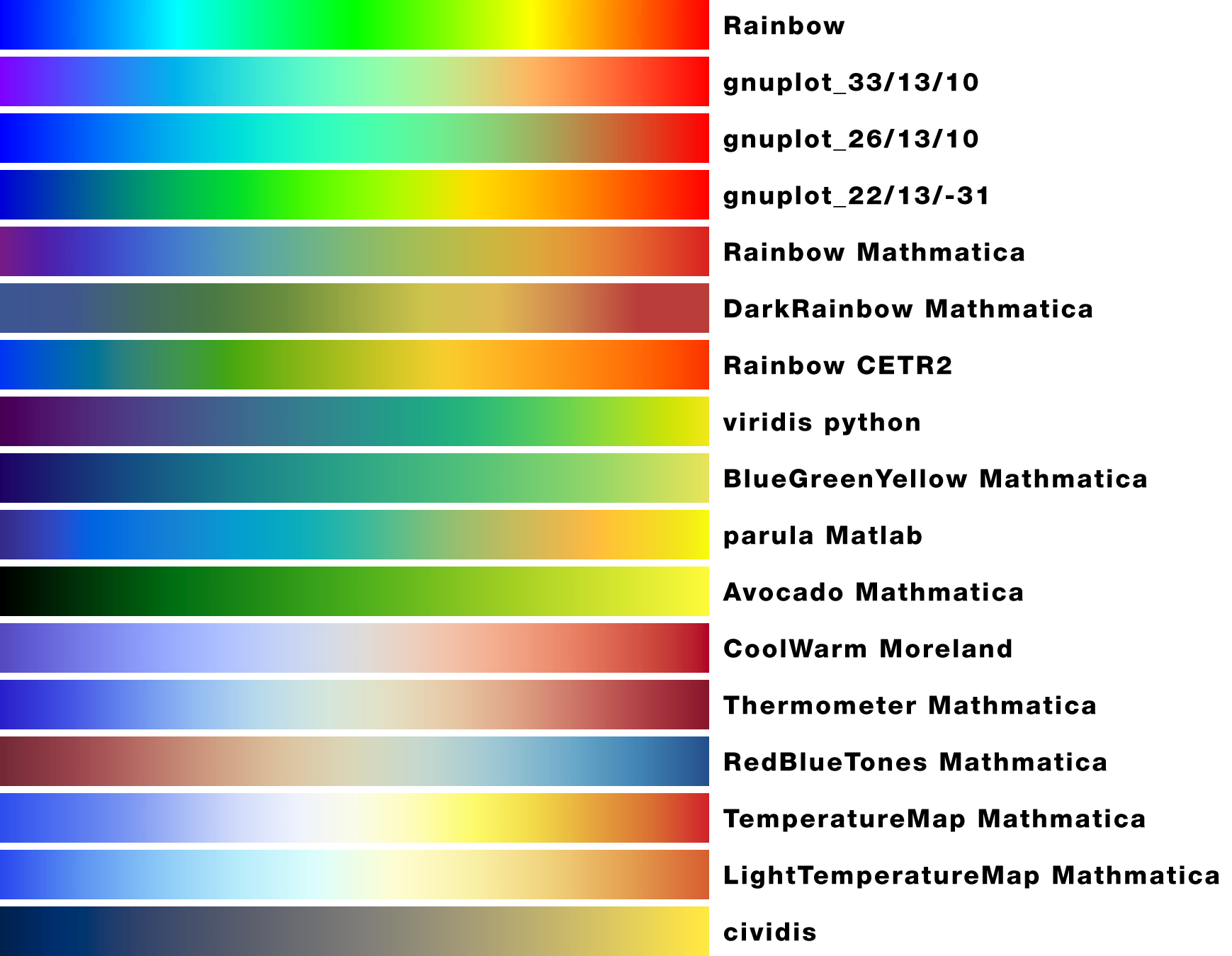
解析表达式的单函数形式
如果所用的编程语言支持 ?: 三元条件运算, 可以将得到的拟合结果写成单个函数的形式, 例如viridis对应的函数三个函数如下:
r= x<=0.455523 ? cubic(x, 0.282113, 0.585552, -3.199668, 3.273305) : \
x<=0.700880 ? cubic(x, -2.797136, 18.565436, -37.531934, 24.521874) : \
x<=1.000000 ? cubic(x, 4.563142, -18.410284, 23.559766, -8.759172) : 0
g= x<=0.074291 ? cubic(x, -0.000438, -0.351490, 48.354922, -360.945985) : \
x<=0.702835 ? cubic(x, -0.014997, 1.564580, -1.154700, 0.700928) : \
x<=1.000000 ? cubic(x, -0.960756, 4.427797, -3.482215, 0.926468) : 0
b= x<=0.476051 ? cubic(x, 0.327782, 1.734561, -4.300750, 3.500006) : \
x<=0.932551 ? cubic(x, 0.218208, 1.243982, -0.736753, -0.849211) : \
x<=1.000000 ? cubic(x, 348.076269, -1047.336499, 1048.282355, -348.910600) : 0python不支持 ?: 运算符, 或者老老实实地if elif, 或者使用一些奇技淫巧.
