- 2019-09-06 19:55:15 整理: 吴伟; 修订: 李继存
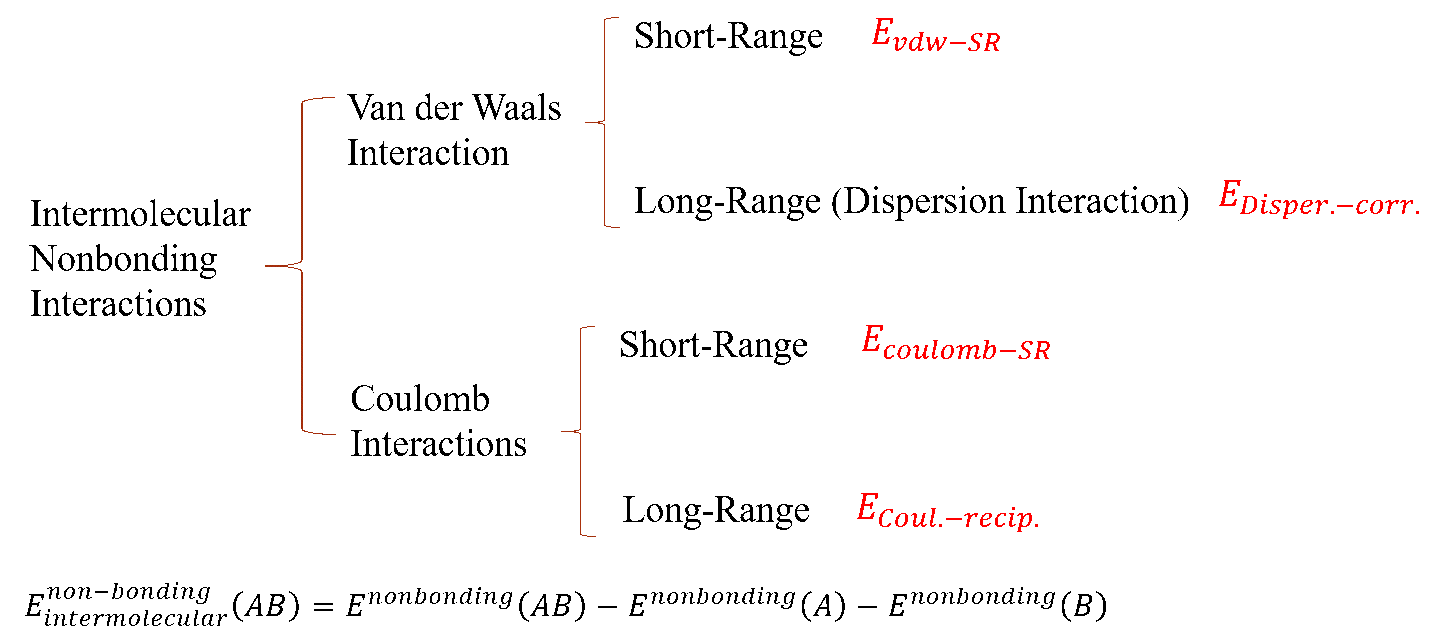
GMX将分子间相互作用分为范德华相互作用和库伦相互作用. 范德华相互作用是短程相互作用, 所以大部分能量都以 EVdw-SR 体现, 而长程部分以色散校正的形式体现, 即 EDisper.-corr.. 库伦相互作用即静电相互作用, 是长程相互作用. GMX处理静电时可以采用两种不同的方式, 截断和PME. 前者用于孤立的团簇体系, 后者用于周期性体系. 如果使用截断方式, 库伦相互作用就是简单的对势加和, 分解也很简单. 如果采用PME方式, 截断距离内的短程库伦 ECoulomb-SR 和倒易空间中的长程库伦 ECoul.-recip. 加起来才是整个体系的库伦相互作用. 这种方法也是能够写成对势累加形式的, 但过于麻烦, 所以一般程序不会支持, 因此也就导致没法直接将整个库伦作用分解到分子之间的贡献. 所以, 使用GMX计算两种或者两种以上分子的分子间相互作用时, 利用能量组功能, 可以直接得到分子间的范德华相互作用, 但对于分子间的库伦作用, 如果你使用了PME的话, 就只能通过相互作用的定义进行计算.
理论是这样, 但实际大多数时候, 我们需要计算的, 或者说我们感兴趣的都是一些孤立分子之间的库伦相互作用, 而不是这些分子处于周期性盒子中, 具有一定浓度情况下的库伦相互作用. 所以你在要进行PME的库伦相互作用能分解之前, 先想一想, 这是不是你需要的. 如果不是, 那你使用简单截断方法, 将截断值设为无穷大, 就可以得到结果了.
如果你铁了心要进行PME库伦相互作用的分解, 那就继续向下看.
方法
体系中有A, B两种分子, 离子和水, 要计算A, B两种分子之间的相互作用
1. 使用 gmx trjconv将A, B的轨迹提取出来
gmx trjconv -f md.xtc -s md.tpr -n -o AB.xtc2. 使用GMX的 rerun 方法, 重跑一遍轨迹, 计算AB体系中的相互作用.
首先需要AB体系的 AB.tpr文件, 所以先抽取一帧只含AB分子的构型
gmx trjconv -f md.gro -s md.tpr -n -o AB.gro编辑拓扑文件, 只留下A和B, 保存为 AB.top, 然后生成tpr文件, 并重跑
gmx grompp -f md.mdp -c AB.gro -p AB.top -o AB.tpr
gmx mdrun -s AB.tpr -rerun AB.xtc -e AB.edr此外, 要获得只含A和B的tpr文件, 使用gmx convert-tpr -n可能更方便.
3. 将轨迹中A组分和B组分的轨迹分别提取出来, 分别用上述方法重跑一遍轨迹, 分别得到A体系和B体系的能量
4. 使用 gmx energy 分析计算相互作用的能量
具体计算方法如下表所示:
| 能量项 | AB | A | B | A-B |
|---|---|---|---|---|
| EVdw-SR | V1 | V2 | V3 | V1-V2-V3 |
| EDisper.-corr. | D1 | D2 | D3 | D1-D2-D3 |
| ECoulomb-SR | C1 | C2 | C3 | C1-C2-C3 |
| ECoul.-recip. | R1 | R2 | R3 | R1-R2-R3 |
| Etotal | V1+D1+C1+R1 | V2+D2+C2+R2 | V3+D3+C3+R3 | (V1+D1+C1+R1)-(V2+D2+C2+R2)-(V3+D3+C3+R3) |
|
注:AB为A和B整个体系的相互作用;A-B为A和B之间的相互作用. | ||||
示例
下面是计算的两种染料分子(各27个)之间的相互作用, 在水溶液中, 染料分子均呈阴离子形式存在(每个染料分子均带两个负电荷).
| 分子间能量项(kJ/mol) | E(AB) | E(A) | E(B) | 分子间相互作用能ΔE(A-B) | ||
|---|---|---|---|---|---|---|
| vdw | LJ(SR) | -2362.31 | -1044.44 | -647.835 | -670.035 | -672.487 |
| Disper.-corr. | -4.28051 | -1.02088 | -0.80754 | -2.452 | ||
| coulomb | Coulomb(SR) | 51184 | 28962.4 | 22365 | -143.4 | 2743 |
| Coul.-recip. | 27988.2 | 12809.1 | 12292.7 | 2886.4 | ||
由于计算的染料是都是阴离子, 相互之间形成聚集体, 虽然短程静电相互作用为负值, 但长程静电相互作用为正值, 总的静电相互作用能为正值, 并且总相互作用能也为正值.
