本手册已过时, 不再更新. 如果需要最新手册, 请加入下方QQ群.
- 4.1 非键相互作用
- 4.2 键合相互作用
- 4.3 限制
- 4.4 极化
- 4.5 自由能相互作用
- 4.6 方法
- 4.7 虚拟相互作用位点
- 4.8 长程静电作用
- 4.9 长程范德华相互作用
- 4.10 力场
为了能够使用一些流行力场中采用的势能函数(见4.10节), GROMACS提供了一些势能函数, 包括非键相互作用以及二面角的相互作用. 我们将在适当的小节中对它们予以讨论.
势能函数可以被划分成三个部分:
非键项: Lennard-Jones或Buckingham, 以及库仑或修正的库仑. 非键相互作用的计算基于已移除了排除项的邻区列表(一定半径内非键原子的列表).
键合项: 共价键伸缩, 键角弯曲, 反常二面角, 和正常二面角. 这些项的计算是基于固定的列表.
约束项: 位置约束, 角度约束, 距离约束, 方向约束和二面角约束, 均基于固定的列表进行计算.
4.1 非键相互作用
GROMACS的非键相互作用是对势累加的(pair-additive), 并满足中心对称:
\[V(\bi r_1, \cdots \bi r_N) = \sum_{i< j} V_{ij}(\bi r_{ij}) \tag{4.1}\]
\[\bi F_i = - \sum_j {dV_{ij}(r_{ij}) \over dr_{ij}} {\bi r_{ij} \over r_{ij}} = - \bi F_j \tag{4.2}\]
非键相互作用包含排斥项, 色散项和库仑项. 组合起来的排斥项和色散项可以取Lennard-Jones(或6–12相互作用)或Buckingham(或exp–6势)形式. 此外, (部分)带电的原子之间的非键相互作用通过库仑项表达.
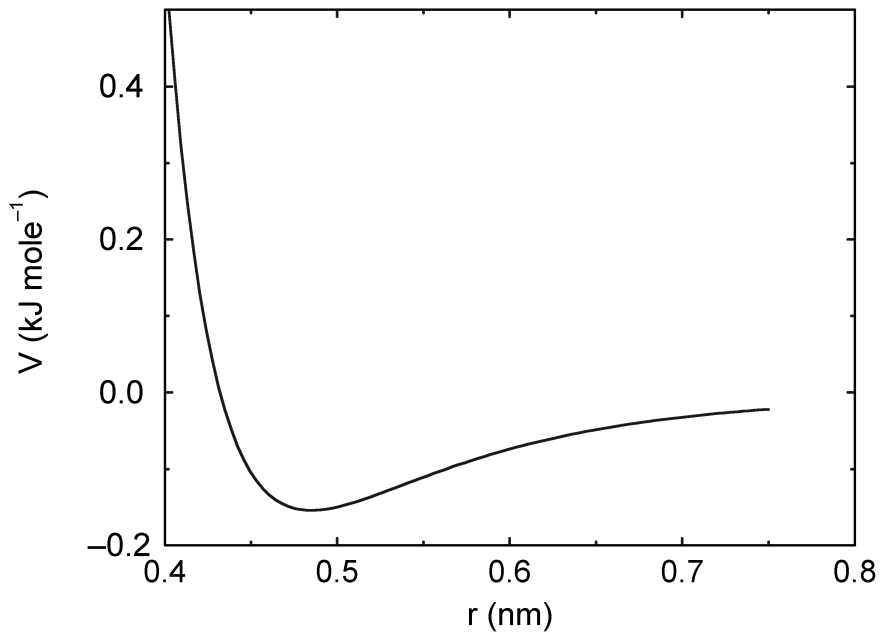
4.1.1 Lennard-Jones相互作用
两个原子之间Lennard-Jones势 \(V_{LJ}(r_{ij})\) 等于:
\[V_{LJ}(r_{ij}) = {C_{ij}^{(12)} \over r_{ij}^{12} } - {C_{ij}^{(6)} \over r_{ij}^6} \tag{4.3}\]
其函数曲线如图4.1所示. 参数 \(C_{ij}^{(12)}\) 和 \(C_{ij}^{(6)}\) 取决于配对的 原子类型; 因此来源于LJ-参数矩阵. 在Verlet截断方案中, 通过将势能移动一个恒量, 可使其在截断距离处为零.
此势能函数的力是:
\[\bi F_i(\bi r_{ij}) = \left(12{C_{ij}^{(12)} \over r_{ij}^{13}} - 6{C_{ij}^{(6)} \over r_{ij}^7}\right){\bi r_{ij} \over r_{ij}} \tag{4.4}\]
LJ势也可以写成以下形式:
\[V_{LJ}(r_{ij}) = 4 \varepsilon_{ij} \left( \left({\sigma_{ij} \over r_{ij}} \right)^{12} - \left({\sigma_{ij} \over r_{ij}}\right)^6 \right) \tag{4.5}\]
在构造非键LJ-参数的参数矩阵时, GROMACS可使用两种不同的组合规则, 只采用几何平均值(力场文件输入部分的类型1):
\[\begin{split} C_{ij}^{(6)} &= \left( C_{ii}^{(6)} C_{jj}^{(6)} \right)^{1/2} \\ C_{ij}^{(12)} &= \left(C_{ii}^{(12)} C_{jj}^{(12)} \right)^{1/2} \end{split} \tag{4.6}\]
或采用Lorentz-Berthelot规则. 此规则利用算术平均计算 \(\s_{ij}\), 利用几何平均计算 \(\ve_{ij}\) (类型2):
\[\begin{split} \sigma_{ij} &= {1 \over 2}(\sigma_{ii} + \sigma_{jj}) \\ \varepsilon_{ij} &= (\varepsilon_{ii} \varepsilon_{jj})^{1/2} \end{split} \tag{4.7}\]
最后, 可以对两个参数都采用几何平均值(类型3):
\[\begin{split} \sigma_{ij} = (\sigma_{ii} \sigma_{jj})^{1/2} \\ \varepsilon_{ij} = (\varepsilon_{ii} \varepsilon_{jj})^{1/2} \end{split} \tag{4.8}\]
OPLS力场就采用这个规则.
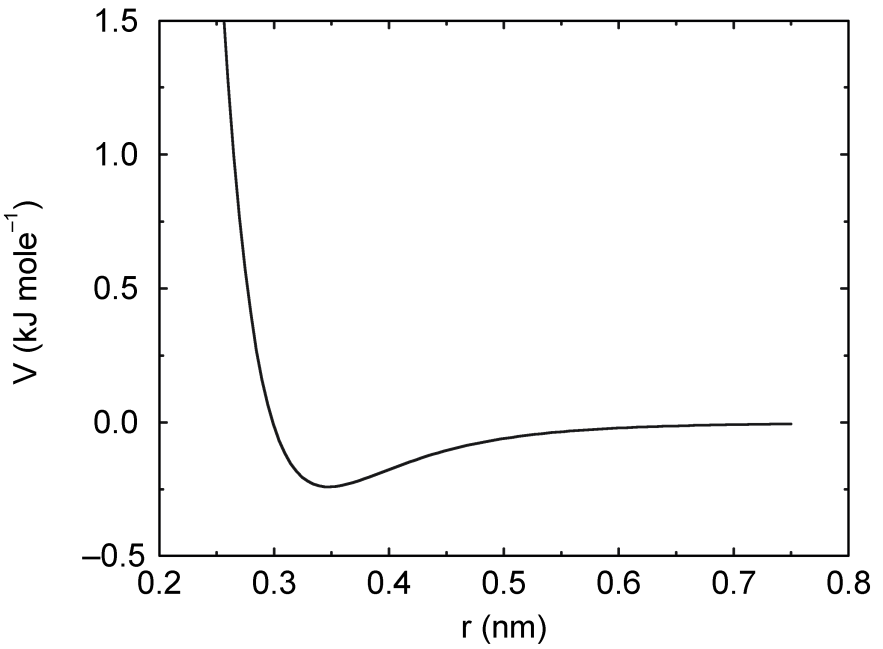
4.1.2 Buckingham势
与Lennard-Jones势相比, Buckingham势的排斥项更加灵活, 贴近实际, 但其计算也更昂贵. Buckingham势的形式是:
\[V_{bh}(r_{ij}) = A_{ij} \exp(-B_{ij} r_{ij}) - {C_{ij} \over r_{ij}^6} \tag{4.9}\]
请参见图4.2. 此势能函数的力为:
\[\bi F_i(r_{ij}) = \left[ A_{ij} B_{ij} \exp(-B_{ij} r_{ij}) - 6{C_{ij} \over r_{ij}^7} \right] {\bi r_{ij} \over r_{ij}} \tag{4.10}\]
4.1.3 库仑相互作用
两个带电粒子之间的库仑相互作用由下式给出:
\[V_c(r_{ij}) = f{q_i q_j \over \varepsilon_r r_{ij}} \tag{4.11}\]
参见图4.3, 其中 \(f={1 \over 4\p\ve_0}=138.935 485\) (见第2章)
此势对应的力为:
\[\bi F_i(r_{ij}) = f{q_i q_j \over \varepsilon_r r_{ij}^2} {\bi r_{ij} \over r_{ij}} \tag{4.12}\]
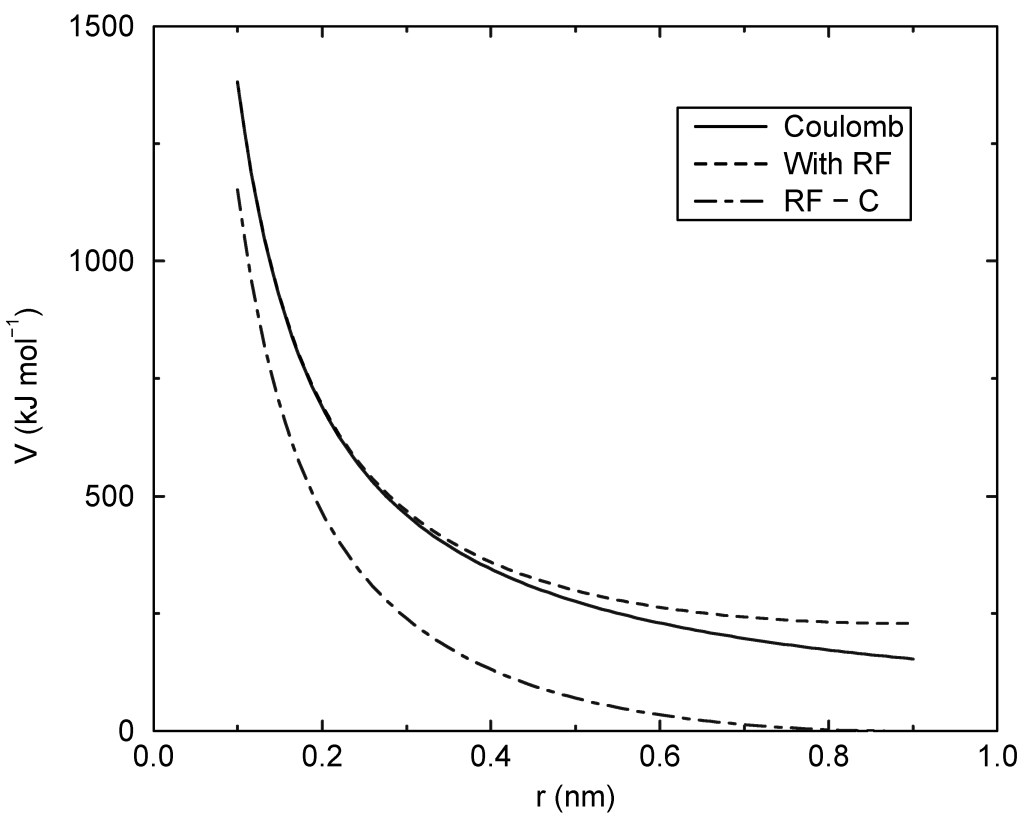
使用普通的库仑相互作用时要么不能截断, 要么所有粒子对都处于截断半径范围内, 因为力在截断处存在跃变, 而且变化很大. 如果你确实需要使用截断, 可以将势能进行移动以使势能等于力的积分. 在基于组的截断方案中, 这种移动只适用于非排除对. 在Verlet截断方案中, 移动也适用于排除对和自相互作用, 这使得势能等同于 \(\ve_{rf}=1\) 的反应场(见下文).
GROMACS中相对介电常数 \(\ve_r\) 可在grompp的输入中设置.
4.1.4 反应场库仑作用
对均相体系, 可通过假定截断半径 \(r_c\) 以外的粒子周围是介电常数为 \(\ve_{rf}\) 的恒定介电环境, 对库仑相互作用进行校正. 此时, 库仑相互作用可写为:
\[V_{crf} = f{q_i q_j \over \varepsilon_r r_{ij}} \left[ 1 + {\varepsilon_{rf} - \varepsilon_r \over 2 \varepsilon_{rf} + \varepsilon_r } {r_{ij}^3 \over r_c^3} \right] - f {q_i q_j \over \varepsilon_r r_c} {3 \varepsilon_{rf} \over 2 \varepsilon_{rf} + \varepsilon_r} \tag{4.13}\]
上式右边的常量表达式使得在截断处势能为零. 对带电的截断球体, 上式对应于均匀背景电荷的中性化. 我们可以将方程4.13简写为
\[V_{crf} = f{q_i q_j \over \varepsilon_r} \left[ {1 \over r_{ij}} + k_{rf} r_{ij}^2 - c_{rf}\right] \tag{4.14}\]
其中,
\[\alg k_{rf} &= {1 \over r_c^3} {\varepsilon_{rf} - \varepsilon_r \over (2 \varepsilon_{rf} + \varepsilon_r)} \tag{4.15} \\ c_{rf} &= {1 \over r_c} + k_{rf} r_c^2 = {1 \over r_c} {3\varepsilon_{rf} \over (2 \varepsilon_{rf} + \varepsilon_r)} \tag{4.16} \ealg\]
对大的 \(\ve_{rf}\), \(k_{rf}\) 趋近 \(r_c^{-3}/2\), 而当 \(\ve_{rf}=\ve_r\) 时校正消失. 图4.3中画出了校正的相互作用, 很显然, 对 \(r_{ij}\) 的导数(即负的力)在截断距离处为零. 这种势函数对应的力为:
\[\bi F_i(\bi r_{ij}) = f{q_i q_j \over \varepsilon_r} \left[ {1 \over r_{ij}^2} - 2 k_{rf} r_{ij} \right]{\bi r_{ij} \over r_{ij}} \tag{4.17}\]
反应场校正也可以用于所有的排除原子对, 包括自身对, 在这种情况下, 方程4.13和4.17中不出现正常的库仑项.
Tironi等引入了更一般的反应场理论, 其截断半径 \(r_c\) 以外的电介质也具有离子强度 \(I\)[75]. 这种情况下, 我们可以利用逆Debye屏蔽长度 \(\kappa\), 将常数 \(k_{rf}\) 和 \(c_{rf}\) 重写为
\[\alg \kappa^2 &= {2IF^2 \over \varepsilon_0 \varepsilon_{rf}RT} = {F^2 \over \varepsilon_0 \varepsilon_{rf}RT} \sum_{i=1}^K c_i z_i^2 \tag{4.18} \\ k_{rf} &= {1 \over r_c^3} { (\varepsilon_{rf}-\varepsilon_r)(1+\kappa r_c) + {1 \over 2}\varepsilon_{rf}(\kappa r_c)^2 \over (2\varepsilon_{rf}+\varepsilon_r)(1+\kappa r_c) + \varepsilon_{rf}(\kappa r_c)^2} \tag{4.19} \\ c_{rf} &= {1 \over r_c} {3 \varepsilon_{rf} (1+\kappa r_c + {1\over2}(\kappa r_c)^2) \over (2 \varepsilon_{rf} + \varepsilon_r)(1+\kappa r_c) + \varepsilon_{rf}(\kappa r_c)^2} \tag{4.20} \ealg\]
其中, \(F\) 是法拉第常数, \(R\) 是理想气体常数, \(T\) 是绝对温度, \(c_i\) 是物种 \(i\) 的摩尔浓度, \(z_i\) 是物种 \(i\) 的电荷数, 共有 \(K\) 种不同的物种. 在离子强度为零的极限情况下, 方程4.19和4.20分别退化为简单形式的方程4.15和4.16.
4.1.5 修正的非键相互作用
在GROMACS中, 可以利用移位函数对非键势能函数进行修改, 其目的在于用连续的力取代截断的力, 且使其在截断半径处具有连续的导数. 使用这种力时, 每步积分引入的误差更小, 且避免了一些复杂情况, 比如在截断过程中由偶极产生的电荷. 实际上, 使用移位力时, 不需要对电荷组创建邻近列表. 然而, 移位函数使库仑势产生了一个相当大的变形. 除非对“丢失”的远程势进行了正确的计算以及加和(通过使用PPPM, Ewald或PME), 否则必须仔细评估这些修改的效果. 对Lennard-Jones色散项和排斥项的修改较小, 但它确实消除了截断效应引起的噪声.
切换函数(将势能乘上一个函数)和移位函数(将势能或力加上一个函数)之间 没有 本质区别[76]. 切换函数是移位函数的一种特殊情况. 将切换函数应用于与粒子 \(j\) 作用在粒子 \(i\) 上的静电力或范德华力有关的 力函数 \(F(r)\):
\[\bi F_i = cF(r_{ij}){\bi r_{ij} \over r_{ij}} \tag{4.21}\]
对于纯的库仑或Lennard-Jones相互作用, \(F(r)= F_\a(r)= r^{-\a+1}\). 移位力 \(F_s(r)\) 一般可写为:
\(\alg F_s(r) &= F_\a (r) & &r < r_1 \\ F_s(r) &= F_\a (r) + S(r) & &r_1 \le r \le r_c \tag{4.22} \\ F_s(r) &= 0 & &r_c \le r \ealg\)
当 \(r_1\) =0 时, 这是一个通常的移动函数, 否则它就是一个切换函数. 相应的移位库仑势为:
\[V_s(r_{ij}) = f \F_s(r_{ij}) q_i q_j \tag{4.23}\]
其中, \(\F(r)\) 是势函数
\[\F_s(r) = \int_r^\infty F_s(x)dx \tag{4.24}\]
GROMACS的移位函数在边界处应该是平滑的, 因此移位函数应当满足以下边界条件:
\(\alg \begin{split} S(r_1) &= 0 \\ S'(r_1) &= 0 \\ S(r_c) &= - F_\a (r_c) \\ S'(r_c) &= - F_\a'(r_c) \end{split} \tag{4.25} \ealg\)
三阶多项式形式
\[S(r) = A(r - r_1)^2 + B(r - r_1)^3 \tag{4.26}\]
即满足这些要求. 常数 \(A\) 和 \(B\) 可利用 \(r_c\) 处的边界条件求出
\[\alg \begin{split} A &= - {(\a + 4)r_c - (\a + 1)r_1 \over r_c^{\a+2}(r_c - r_1)^2} \\ B &= {(\a+3)r_c - (\a+1)r_1 \over r_c^{\a+2} (r_c-r_1)^3} \end{split}\tag{4.27} \ealg\]
因此, 整个力函数为:
\[F_s(r) = {\a \over r^{\a+1}} + A(r-r_1)^2 + B(r-r_1)^3 \tag{4.28}\]
相应的势函数为:
\[\F(r) = {1 \over r^\a} - {A \over 3}(r - r_1)^3 - {B \over 4}(r - r_1)^4 - C \tag{4.29}\]
其中
\[C = {1 \over r_c^\a } - {A \over 3}(r_c - r_1)^3 - {B \over 4}(r_c - r_1)^4 \tag{4.30}\]
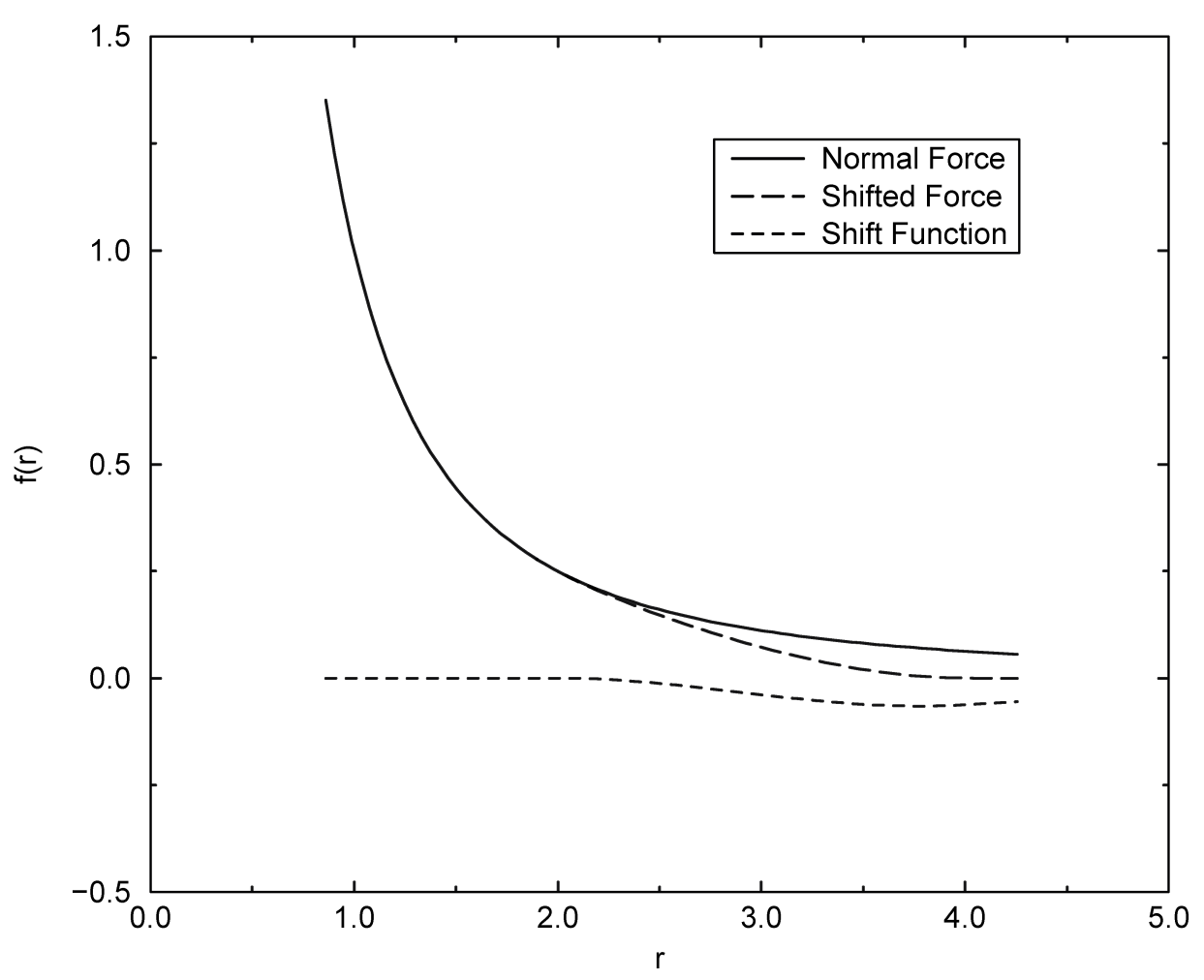
当 \(r_1\) =0 时, 修正的库仑力函数
\[F_s(r) = {1 \over r^2} - {5 r^2 \over r_c^4} + {4 r^3 \over r_c^5} \tag{4.31}\]
与推荐使用的短程函数加上长程部分的泊松解是相同的[77]. 修正的库仑势函数为:
\[\F(r) = {1 \over r} - {5 \over 3r_c} + {5r^3 \over 3r_c^4} - {r^4 \over r_c^5} \tag{4.32}\]
参见图 4.4.
4.1.6 修改的Ewald求和短程相互作用
当利用Ewald求和方法或粒子网格Ewald方法计算长程相互作用时, 短程库仑势必须进行修改, 这与上面切换函数的情形类似. 在这种情况下, 短程势能由下式给出:
\[V(r) = f{\text{erfc}(\beta r_{ij}) \over r_{ij}} q_i q_j \tag{4.33}\]
其中, \(\b\) 参数用于决定直接空间和与倒易空间和之间的相对比重, \(\text{erfc}(x)\) 是余误差函数. 关于长程静电相互作用的详细讨论见4.8节.
4.2 键合相互作用
键合相互作用基于固定的原子列表. 它们不仅包括对相互作用(pair interactions), 也包括三体和四体相互作用. 键合相互作用包括 键伸缩(双体), 键角(三体)和 二面角(四体)相互作用. 一种特殊类型的二面角相互作用(称为 异常二面角)可用于将原子保持在同一平面上, 或是避免将分子转变为相反手性(镜像)的结构.
4.2.1 键伸缩
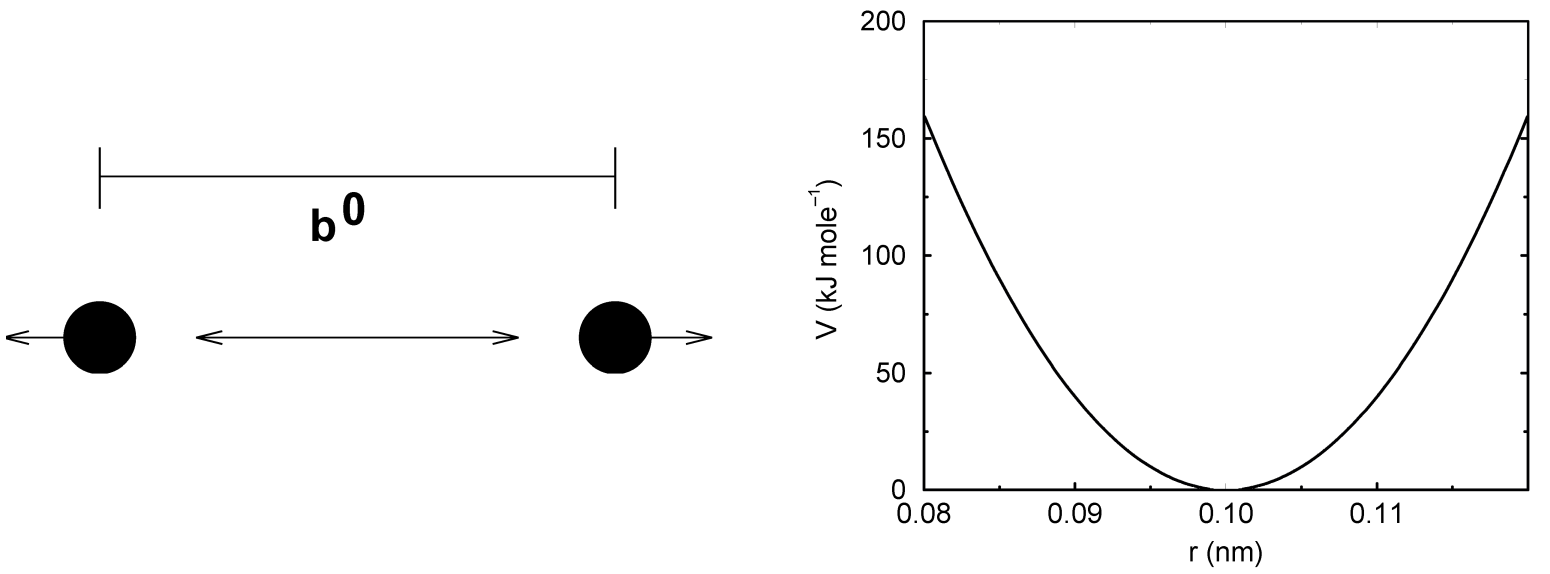
简谐势
两个共价键合原子 \(i\) 和 \(j\) 之间的键伸缩可利用简谐势进行描述
\[V_b(r_{ij}) = {1 \over 2}k_{ij}^b (r_{ij} - b_{ij})^2 \tag{4.34}\]
参见图4.5, 相应的力如下:
\[\bi F_i(\bi r_{ij}) = k_{ij}^b(r_{ij} - b_{ij}) {\bi r_{ij} \over r_{ij}} \tag{4.35}\]
四次幂势
在GROMOS–96力场[78]中, 为提高计算效率, 共价键势记为以下形式:
\[V_b(r_{ij}) = {1 \over 4}k_{ij}^b \left( r_{ij}^2 - b_{ij}^2 \right)^2 \tag{4.36}\]
相应的力为:
\[\bi F_i(\bi r_{ij}) = k_{ij}^b(r_{ij}^2 - b_{ij}^2) \bi r_{ij} \tag{4.37}\]
对这种形式的势函数, 其力常数与通常的简谐力常数 \(k^{b,\text{harm}}\) (4.2.1节) 存在如下关系
\[2k^b b_{ij}^2 = k^{b,\text{harm}} \tag{4.38}\]
力常数大多是由GROMOS–87使用的简谐力常数导出[79]. 尽管计算时这种形式效率更高(因为不需要计算平方根), 但它在概念上比较复杂. 它还存在一个特别的缺点, 由于不是简谐势形式, 单个键的平均能量不等于 \({1\over2}kT\), 而在正常的简谐势情况下是 \({1\over2}kT\).
4.2.2 Morse势键伸缩
对需要非简谐键伸缩势的一些体系, GROMACS提供了两个原子 \(i\) 和 \(j\) 之间的Morse势[80]. 这个势能函数与简谐势的不同在于, 它具有一个不对称的势阱, 且无限远处的力为零. 函数形式是:
\[V_{morse}(r_{ij}) = D_{ij} [1 - \exp(-\beta_{ij} (r_{ij}-b_{ij}))]^2 \tag{4.39}\]
参见图4.6, 相应的力是:
\[\bi F_{morse}(\bi r_{ij}) = 2 D_{ij} \beta_{ij} r_{ij} \exp(-\beta_{ij}(r_{ij}-b_{ij}))* \\ [1 - \exp(-\beta_{ij} (r_{ij}-b_{ij}))] {\bi r_{ij} \over r_{ij}} \tag{4.40}\]
其中 \(D_{ij}\) 是势阱深度, 以 \(\text{kJ/mol}\) 为单位, \(\beta_{ij}\) 定义了势阱的陡度(以 \(\text{nm^{-1}}\) 为单位), \(b_{ij}\) 为平衡距离(以 \(\text{nm}\) 为单位). 陡度参数 \(\beta_{ij}\) 可用原子 \(i\) 和 \(j\) 的约化质量、基本振动频率 \(\mu_{ij}\) 和势阱深度 \(D_{ij}\) 表示:
\[\beta_{ij} = \omega_{ij} \sqrt{\mu_{ij} \over 2 D_{ij} } \tag{4.41}\]
且因为 \(\omega = \sqrt{k \over \mu}\), 可将 \(\beta_{ij}\) 改用简谐力常数 \(k_{ij}\) 表示:
\[\beta_{ij} = \sqrt{k_{ij} \over 2 D_{ij}} \tag{4.42}\]
对于小的偏差 \((r_{ij} - b_{ij})\), 可利用泰勒展开, 取指数项的一阶近似:
\[\exp(-x) \approx 1 - x \tag{4.43}\]
将方程 4.42和4.43代入到函数中:
\[\alg V_{morse}(r_{ij}) &= D_{ij} [1 - \exp(-\beta_{ij} (r_{ij}-b_{ij}))]^2 \\ & = D_{ij} [1 - (1 - \sqrt{k_{ij} \over 2 D_{ij}} (r_{ij}-b_{ij}))]^2 \\ & = {1 \over 2} k_{ij} (r_{ij} - b_{ij})^2 \tag{4.44} \ealg\]
就得到了简谐键伸缩势.
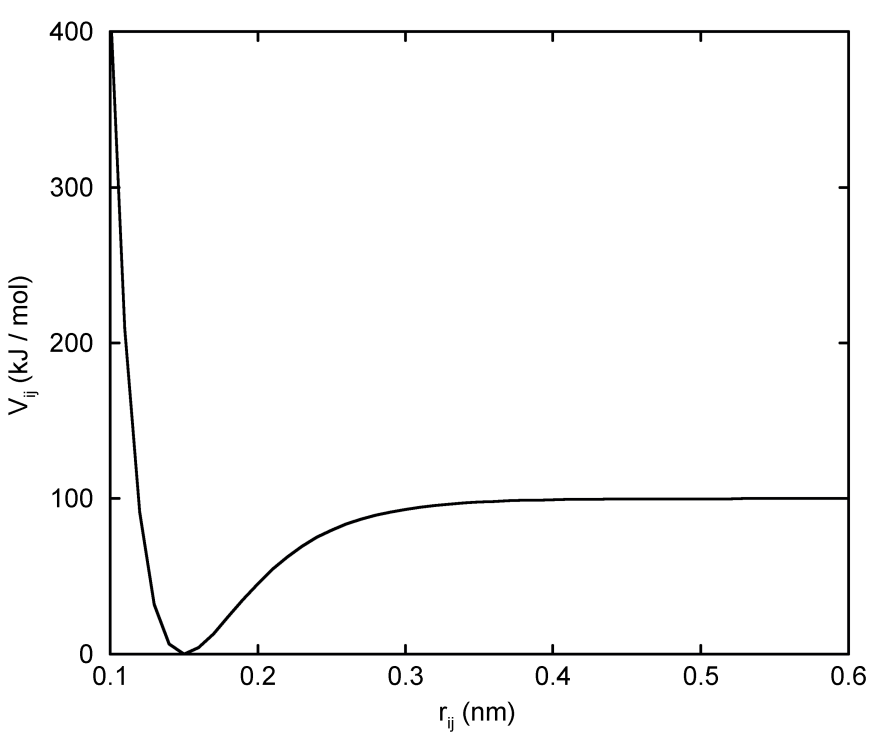
4.2.3 立方键伸缩势
另一种比Morse势稍简单的非简谐键伸缩势是在简单的简谐形式上增加了距离的一个立方项:
\[V_b(r_{ij}) = k_{ij}^b (r_{ij}-b_{ij})^2 + k_{ij}^b k_{ij}^{cub} (r_{ij}-b_{ij})^3 \tag{4.45}\]
在Ferguson[82]发展的一个柔性水模型(基于SPC水模型[81])中, OH键使用了立方键伸缩势. 该模型给出了合理的红外光谱. GROMACS库中提供了Ferguson水模型(flexwat-ferguson.itp). 应当指出, 这种势函数是不对称的: 过分拉伸导致能量无限降低. 因此积分的时间步长被限制为1 fs.
该势对应的力为:
\[\bi F_i(r_{ij}) = 2k_{ij}^b (r_{ij}-b_{ij}) {\bi r_{ij} \over r_{ij}} + 3k_{ij}^b k_{ij}^{cub} (r_{ij}-b_{ij})^2 {\bi r_{ij} \over r_{ij}} \tag{4.46}\]
4.2.4 FENE键伸缩势
在聚合物的粗粒化模拟中, 珠子之间通常由FENE(finitely extensible nonlinear elastic, 有限扩展非线弹性)势[83]连接:
\[V_{\text{FENE}}(r_{ij}) = - {1 \over 2} k_{ij}^b b_{ij}^2 \log\left( 1 - {r_{ij}^2 \over b_{ij}^2} \right) \tag{4.47}\]
这种势能函数看起来很复杂, 但力的表达式更简单:
\[\bi F_{\text{FENE}}(r_{ij}) = - k_{ij}^b \left( 1 - {r_{ij}^2 \over b_{ij}^2} \right)^{-1} \bi r_{ij} \tag{4.48}\]
在短距离处此势不对称地接近力常数为 \(k^b\) 的简谐势, 而在距离为 \(b\) 时发散.
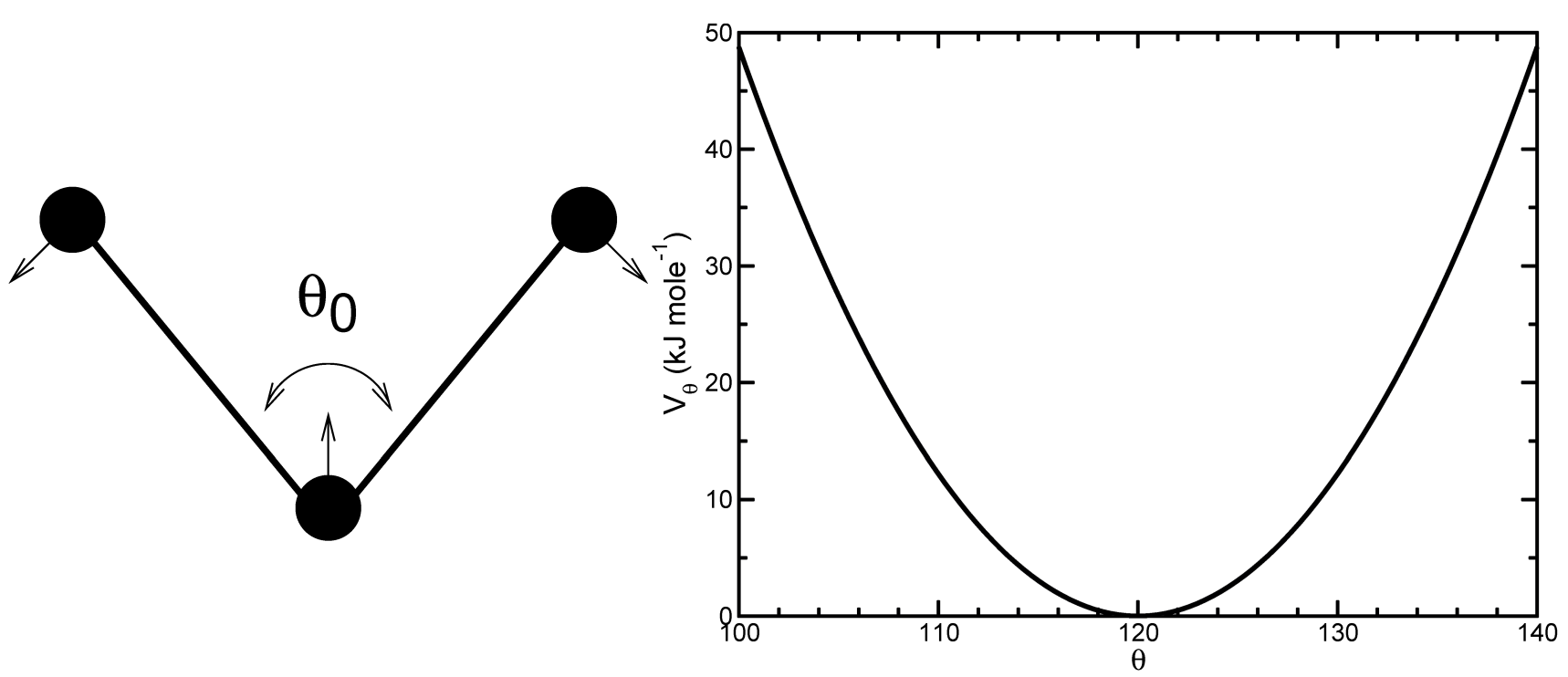
4.2.5 简谐角势
三个原子 \(i-j-k\) 之间的键角振动也可以用键角 \(\theta_{ijk}\) 的简谐势描述
\[V_a (\theta_{ijk}) = {1 \over 2} k_{ijk}^\theta (\theta_{ijk} - \theta_{ijk}^0)^2 \tag{4.49}\]
由于键角的振动由简谐势描述, 其形式与键伸缩是一样的(图4.5).
利用链式规则, 可得到力的方程:
\[\alg \bi F_i &= - {d V_a(\theta_{ijk}) \over d \bi r_i} \\ \bi F_k &= - {d V_a(\theta_{ijk}) \over d \bi r_k} \quad 其中 \theta_{ijk} = \arccos{ (\bi r_{ij} \cdot \bi r_{kj}) \over r_{ij} r_{kj} } \tag{4.50} \\ \bi F_j &= - \bi F_i - \bi F_k \ealg\]
编号 \(i, j, k\) 是共价键原子的序列. 原子 \(j\) 处于中间;原子 \(i\) 和 \(k\) 处于顶端(见图4.7). 注意, 在拓扑文件的输入中, 键角以度为单位, 力常数以 \(\text{kJ/mol/{rad}^2}\) 为单位.
4.2.6 余弦键角势
GROMOS–96力场利用一个简化的函数表示角振动:
\[V_a(\theta_{ijk}) = {1 \over 2} k_{ijk}^\theta \left( \cos(\theta_{ijk}) - \cos(\theta_{ijk}^0) \right)^2 \tag{4.51}\]
其中
\[\cos(\theta_{ijk}) = {\bi r_{ij} \cdot \bi r_{kj} \over r_{ij} r_{kj} } \tag{4.52}\]
相应的力可通过对原子位置的偏微分推导出来. 这个函数中的力常数与简谐势的力常数 \(k^{\theta,\text{harm}}\) (4.2.5) 存在如下关系
\[k^\theta \sin^2(\theta_{ijk}^0) = k^{\theta,\text{harm}} \tag{4.53}\]
在GROMOS–96手册中有一个更加复杂的, 与温度相关的转换公式. 这些公式在0 K时是等效的, 300 K时的差异大约为0.1%到0.2%. 注意 在拓扑文件的输入中, 角度的单位为度, 力常数的单位为kJ/mol.
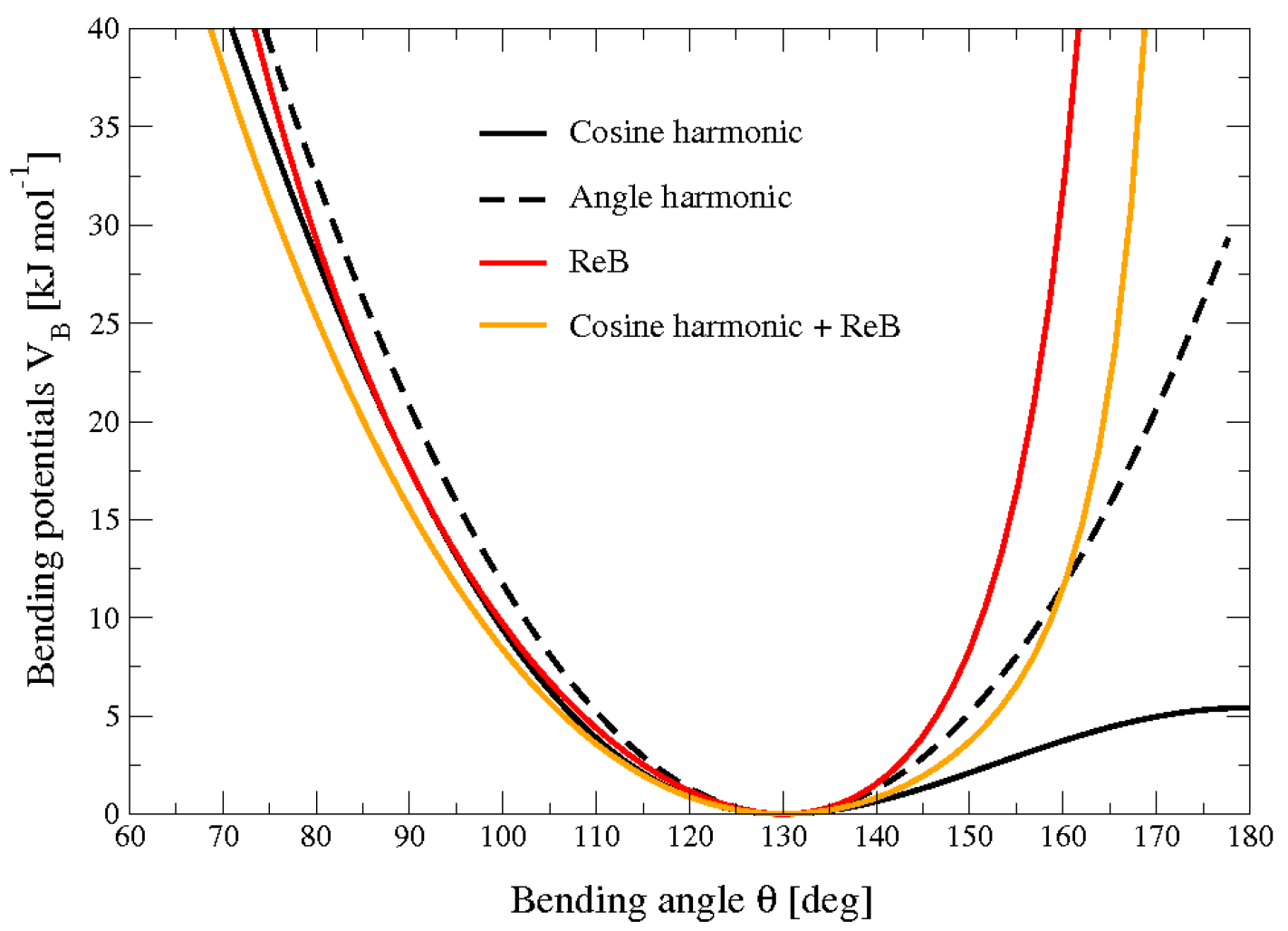
4.2.7 受限弯曲势
受限弯曲(ReB)势[84]可防止弯曲角度 \(\theta\) 达到 \(180^{\circ}\). 这样, 在进行粗粒分子动力学模拟时, 避免了计算扭转角和势能带来的数值不稳定性.
为了系统地防止弯曲角度达到 \(180^{\circ}\), 在弯曲势4.51的分母项中引入了 \(\sin^2\theta\) 因子
\[V_{\text{ReB}}(\theta_i)={1 \over 2} k_\theta {(\cos\theta_i-\cos\theta_0)^2 \over \sin^2\theta_i} \tag{4.54}\]
图4.8显示了ReB势4.54和标准势4.51之间的比较. ReB势的壁垒在靠近 \(180^{\circ}\) 的区域非常排斥, 因此, 弯曲角能够保持在一定的安全区间内, 远离不稳定性. 之所以在分母中使用 \(\sin\theta\) 的二次方项是为了保证这种行为, 并且能给出优雅的微分表达式:
\[F_{\text{ReB}}(\theta_i) = {2 k_\theta \over \sin^4\theta_i}(\cos\theta_i-\cos\theta_0)(1-\cos\theta_i \cos\theta_0){\partial \cos\theta_i \over \partial \vec r_k} \tag{4.55}\]
因其构造, 限制弯曲势不能用于平衡的 \(\theta_0\) 值太接近 \(0^{\circ}\) 或 \(180^{\circ}\) 的情形(根据经验, 推荐至少有 \(10^{\circ}\) 的差异). 重要的是, 在初始构型中, 所有的弯曲角度都必须处在安全的区间内, 以避免初始的不稳定性. 这种弯曲势可以与任何形式的扭转势联合使用. 使用它将总是能够避免三个连续的粒子变成共线结构, 因此, 任何扭转势都不会出现奇点. 也可以将它加入到标准的弯曲势中, 以处理约 \(180^{\circ}\) 的角, 但在极小点附近保持它的原始形式(参见图4.8中的橙色曲线).
4.2.8 Urey-Bradley势
三个原子 \(i - j - k\) 之间的Urey-Bradley键角振动用角 \(\theta_{ijk}\) 的简谐势和原子 \(i\) 和 \(k\) 之间的距离的简谐校正项来描述. 尽管可以很容易地将它写成两项的简单加和, 但方便的做法是把它作为拓扑文件中的单独一项, 并在在输出文件中作为单独的能量项. 这种势能主要用在CHARMM力场[85]中. 其能量由下式给出:
\[V_a(\theta_{ijk})={1\over2}k_{ijk}^\theta(\theta_{ijk}-\theta_{ijk}^0)^2 + {1\over2}k_{ijk}^{UB}(r_{ik}-r_{ik}^0)^2 \tag{4.56}\]
力的方程可从4.2.1和4.2.5节推导出来.
4.2.9 键键交叉项
形成键 \(i - j\) 和 \(k - j\) 的三个粒子 \(i,j,k\) 之间的键键交叉项由下式给出[86]:
\[V_{rr'}=k_{rr'}(\abs{\bi r_i-\bi r_j}-r_{1e})(\abs{\bi r_k-\bi r_j}-r_{2e}) \tag{4.57}\]
其中 \(k_{rr'}\) 是力常数, \(r_{1e}\) 和 \(r_{2e}\) 分别是键 \(i - j\) 和 \(j - k\) 的平衡键长. 此势对应的粒子 \(i\) 受到的力是:
\[\bi F_i=-k_{rr'}(\abs{\bi r_k-\bi r_j}-r_{2e}){\bi r_i-\bi r_j \over \abs{\bi r_i-\bi r_j}} \tag{4.58}\]
原子 \(k\) 受到的力可以通过交换上述方程中 \(i\) 和 \(k\) 得到. 最后, 原子 \(j\) 受到的力遵循内力之和应该为零的事实: \(\bi F_j = - \bi F_i - \bi F_k\).
4.2.10 键-角交叉项
为形成键 \(i - j\) 和 \(k - j\) 的三个粒子 \(i,j,k\) 之间的键-角交叉项由下式给出[86]:
\[V_{k\theta}=k_{r\theta}(\abs{\bi r_i-\bi r_k}-r_{3e})(\abs{\bi r_i-\bi r_j}-r_{1e}+\abs{\bi r_k-\bi r_j}-r_{2e}) \tag{4.59}\]
其中 \(k_{r\theta}\) 为力常数, \(r_{3e}\) 为 \(i - k\) 之间的距离, 其他常数的含义与方程4.57中相同. 原子 \(i\) 受到的力为:
\[\bi F_i = -k_{r\theta}\left[ (\abs{\bi r_i-\bi r_k}-r_{3e}){\bi r_i-\bi r_j \over \abs{\bi r_i-\bi r_j}}+(\abs{\bi r_i-\bi r_j}-r_{1e}+\abs{\bi r_k-\bi r_j}-r_{2e}) {\bi r_i-\bi r_k \over \abs{\bi r_i-\bi r_k}} \right] \tag{4.60}\]
4.2.11 四次键角势
键角势可以使用四阶多项式以满足特殊目的
\[V_q(\theta_{ijk})=\sum_{n=0}^5 C_n(\theta_{ijk}-\theta_{ijk}^0)^n \tag{4.61}\]
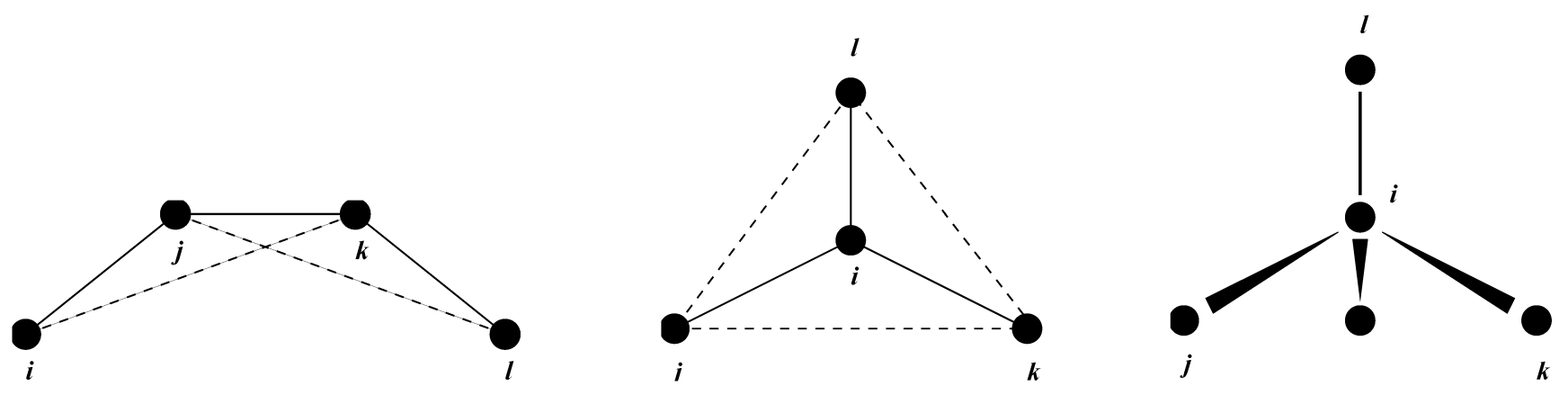
4.2.12 异常二面角
异常二面角是为了保持平面基团(例如芳环)处于平面内, 或者为了防止分子翻转成其镜像分子, 见图4.9.
异常二面角: 简谐型
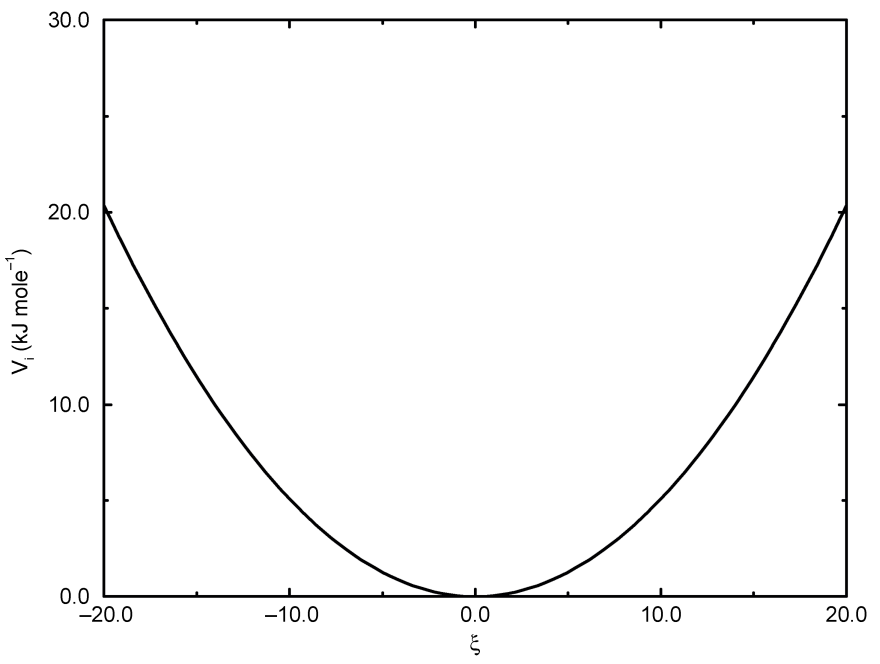
最简单的异常二面角势是简谐势, 曲线如图4.10.
\[V_{id}(\x_{ijkl}) = {1\over2}k_\x(\x_{ijkl}-\x_0)^2 \tag{4.62}\]
简谐势函数不连续, 但由于不连续点选择在距离 \(\x_0\) 为 \(180^{\circ}\) 的位置, 这种不连续性永远不会引出麻烦. 注意, 在拓扑输入文件中, 角度的单位为度, 而力常数的单位为 \(\text{kJ/mol/rad}^2\).
异常二面角: 周期型
这种势函数等同于周期性的正常二面角(见下文). 将此种二面角类型(类型4)单独分类只是为了在参数部分和输出中将异常二面角和正常二面角区分开来.
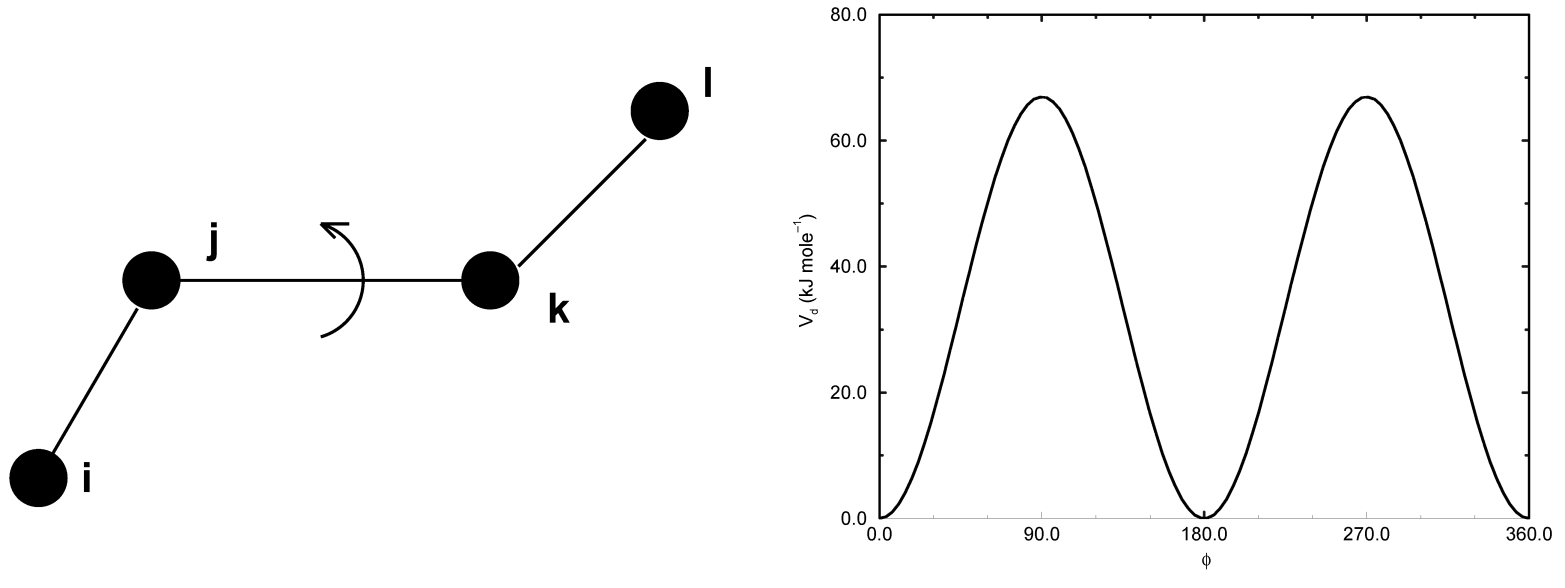
4.2.13 正常二面角
对于正常的二面角相互作用, 可以选择GROMOS的周期性函数或基于 \(\cos\phi\) 的幂的多项式展开函数(被称为Ryckaert-Bellemans势). 这种选择使得二面角四个原子中的第一和第四个原子之间的特殊相互作用也被包含在内.
对周期性的GROMOS势, 必须包含特殊的1–4 LJ-相互作用;对 烷烃 的Ryckaert-Bellemans势, 1–4相互作用必须从非键列表中排除. 注意: Ryckaert-Bellemans势也可在OPLS等力场中与1–4相互作用联合使用. 因此, 在这种情况下你不应该修改pdb2gmx生成的拓扑文件.
正常二面角: 周期型
正常二面角的定义遵从IUPAC/IUB约定, 其中, \(\f\) 是面 \(ijk\) 和面 \(jkl\) 之间的夹角, 零 相应于 顺式(cis) 构型(\(i\) 和 \(l\) 处于面的同一侧). GROMACS拓扑文件中有两类二面角函数类型. 标准类型1的行为和其他的键相互作用类似. 对某些力场, 类型9很有用. 当在[dihedraltypes]部分对同一原子类型定义了多个参数时, 类型9可使多个势能函数自动用于在[dihedral]部分的一个单一的二面角上.
这种类型的势函数为
\[V_d(\phi_{ijkl})=k_\phi(1+\cos(n\phi-\phi_s)) \tag{4.63}\]
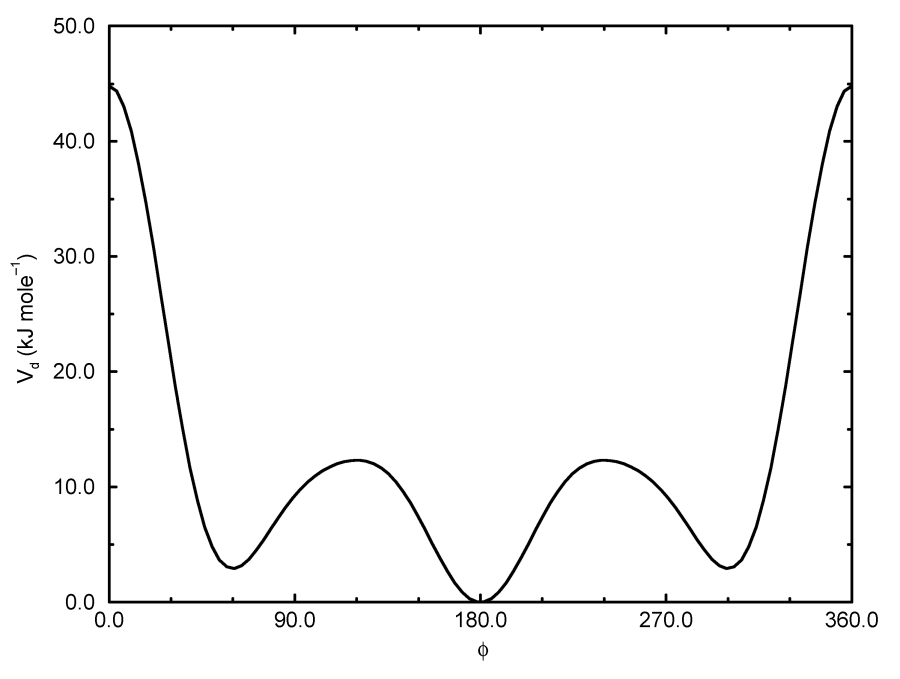
正常二面角: Ryckaert-Bellemans势函数
对烷烃, 经常使用以下的正常二面角势(见图4.12):
\[V_{rb}(\phi_{ijkl})=\sum_{n=0}^5 C_n(\cos(\psi))^n \tag{4.64}\]
其中, \(\psi = \phi - 180^{\circ}\).
注意: 从一个约定到另一个约定的转换可以通过将每个系数 \(C_n\) 乘上 \({-1}^n\).
常数C的一个示例在表4.1中给出.
| C0 9.28 | C2 -13.12 | C4 26.24 |
| C1 12.16 | C3 -3.06 | C5 -31.5 |
(注意: 使用这种势函数意味着排除了组成二面角的第一个和最后一个原子之间的LJ相互作用, 并且 \(\psi\) 的定义遵从“聚合物约定”(\(\psi_{trans} = 0\)).
RB二面角函数也可用于包含傅立叶二面角(见下文):
\[V_{rb}(\phi_{ijkl})={1\over2}[F_1(1+\cos(\phi))+F_2(1-\cos(2\phi))+F_3(1+\cos(3\phi))+F_4(1-\cos(4\phi)) ] \tag{4.65}\]
由于存在等式 \(\cos(2\phi)=2\cos^2(\phi)-1, \cos(3\phi)=4\cos^3(\phi)-3\cos(\phi)\) 和 \(\cos(4\phi)=8\cos^4(\phi)-8\cos^2(\phi)+1\), 可以利用下面的方程将OPLS参数变换为Ryckaert-Bellemans参数
\[\begin{split} C_0 &= F_2 +{1\over2}(F_1+F_3) \\ C_1 &= {1\over2}(-F_1+3F_3) \\ C_2 &= -F_2+4F_4 \\ C_3 &= -2F_3 \\ C_4 &= -4F_4 \\ C_5 &= 0 \end{split} \tag{4.66}\]
OPLS参数遵从蛋白质约定, 而RB参数遵从聚合物约定(这导致 \(\cos(\phi)\) 奇数次项前面的负号).
注意: 记得将文献中OPLS和RB参数的单位 \(\text{kcal mol}^{-1}\) 转化为GROMACS中的单位 \(\text{kcal mol}^{-1}\).
正常二面角: 傅立叶函数
OPLS势能函数为傅立叶级数的前三或四次余弦项[87]. GROMACS中, 四项函数为:
\[V_F(\phi_{ijkl})={1\over2}[C_1(1+\cos(\phi)) + C_2(1-\cos(2\phi)) + C_3(1+\cos(3\phi)) + C_4(1+\cos(4\phi))] \tag{4.67}\]
GROMACS在内部使用Ryckaert-Bellemans代码来计算傅立叶二面角(见上文), 因为计算效率更高.
注意: 记得将文献中OPLS参数的单位 \(\text{kcal mol}^{-1}\) 转化为GROMACS中的单位 \(\text{kcal mol}^{-1}\).
正常二面角: 限制扭转势
非常类似于限制弯曲势(见4.2.7), 限制扭转/二面角势的函数为:
\[V_{\text{ReT}}(\phi_i)={1\over2}k_\phi {(\cos\phi_i-\cos\phi_0)^2 \over \sin^2\phi_i} \tag{4.68}\]
这类函数具有 \(\cos\phi\) 函数的优点(对 \(\sin\phi\) 求导时不存在问题), 并且能保持扭转角处于仅有的一个最小值. 在这种情况下, 因子 \(\sin^2\phi\) 不会让二面角从[ \(-180^{\circ}:0\) ]区间移到[ \(0:180^{\circ}\) ]区间内, 即, 函数不能同时在 \(-\phi_0\) 和 \(+\phi_0\) 处取极大值, 而只能在其中之一取极大值. 由于这个原因, 初始构型中所有的二面角的角度值都必须处于所需的角度区间内, 并且平衡的 \(\phi_0\) 值不应太靠近区间的端点(与4.2.7中所讲的限制弯曲势类似, 推荐至少 \(10^{\circ}\) 的差异).
正常二面角: 组合弯曲-扭转势
当形成二面角的四个粒子共线时(这种情况永远不会发生在原子尺度的模拟中, 但可能出现在粗粒模拟中), 扭转角及其势函数的计算会引起数值不稳定性. 避免这一问题的一种方法是使用限制弯曲势(见4.2.7), 以防止二面角达到 \(180^{\circ}\).
另一种方式是忽略二面角不合理定义时的任何效应, 通过将扭转势(余弦形式)与相邻弯曲角的弯曲势耦合为一个特殊形式, 保持二面角的力和势函数的计算在整个角度范围内连续:
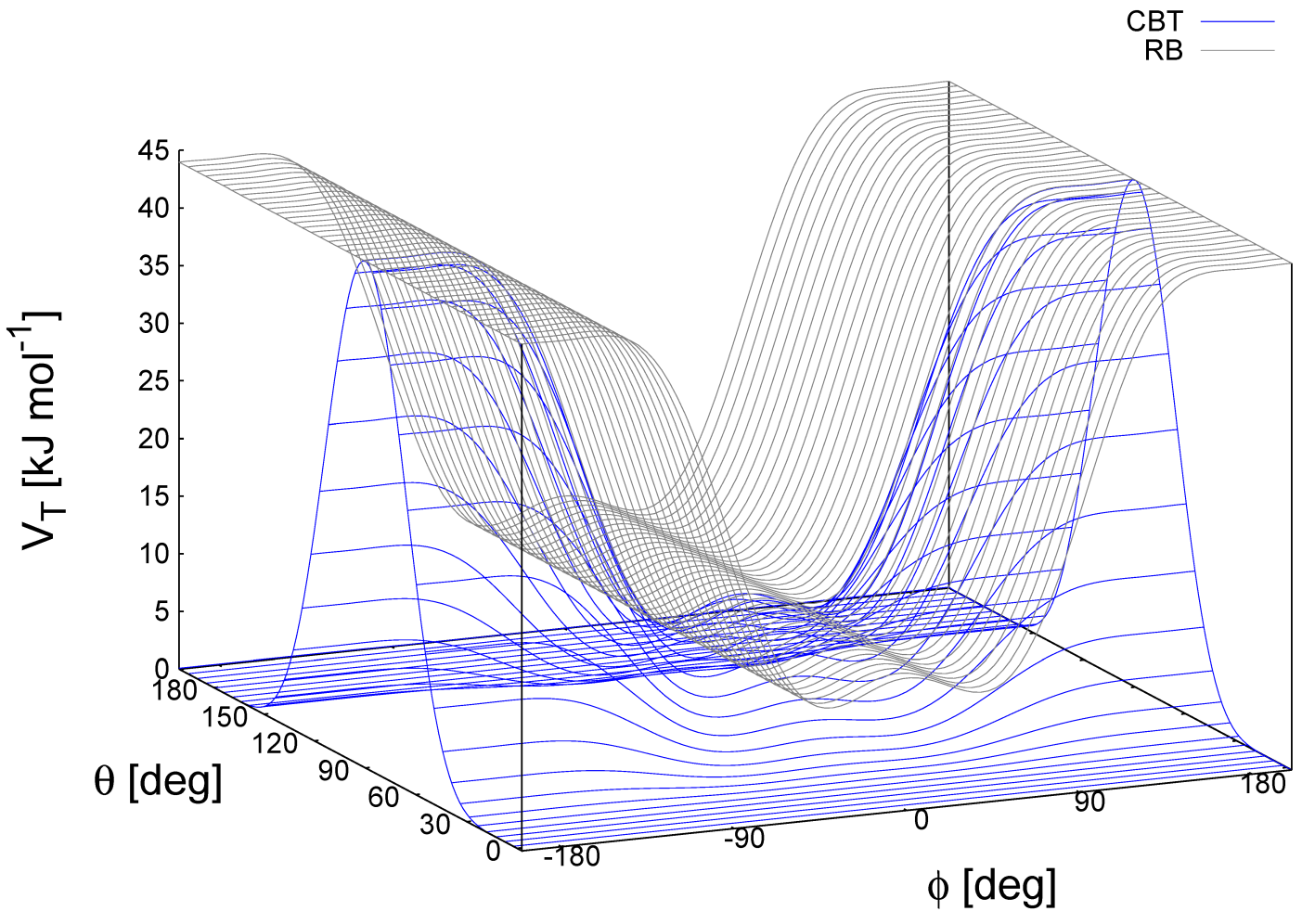
\[V_{\text{CBT}}(\theta_{i-1},\theta_i,\phi_i)=k_\phi \sin^3\theta_{i-1} \sin^3\theta_i \sum_{n=0}^4 a_n \cos^n \phi_i \tag{4.69}\]
这种组合的弯曲扭转(combined bending-torsion, CBT)势函数由文献[88]提出, 用于聚合物熔融的模拟. 文献[84]对此有详细的描述.
这种势函数有两个主要的优点:
它不仅取决于(第 \(i-2, i-1, i\) 和 \(i+1\) 号珠子之间的)二面角 \(\phi_i\), 而且也取决于由三个相邻的珠子(分别是 \(i-2, i-1, i\) 和 \(i-1, i, i+1\))形成的弯曲角 \(\theta_{i-1}\) 和 \(\theta_i\). 当两个弯曲角中的任意一个接近 \(180^{\circ}\) 时, 由文献[89]尝试性地提出, 并由文献[90]从理论上进行了讨论的两个 \(\sin^3\theta\) 前因子抵消了扭转势和力.
通过表达为 \(\cos\phi_i\) 的多项式形式, 它也取决于 \(\phi_i\), 这避免了 \(\phi = 0^{\circ}\) 或 \(\phi = 180^{\circ}\) 时计算扭转力的奇异性.
这两种特性使得CBT势用于弯曲角存在弱约束的MD模拟时表现良好, 甚至对于弯曲角和扭转角变化剧烈的拉伸/非平衡MD模拟也是如此. 当使用CBT势时, 相邻的 \(\theta_{i-1}\) 和 \(\theta_i\) 的弯曲势可以取任意形式, 也可完全省略这两个角弯曲项(\(\theta_{i-1}\) 和 \(\theta_i\)). 图4.13显示了包含和不含 \(\sin^3\theta\) 因子(分别为蓝色和灰色的曲线)的扭转势之间的区别. 此外, \(V_{\text{CBT}}\) 对笛卡尔变量的导数直接易懂:
\[\opar{V_{\text{CBT}}(\theta_{i-1},\theta_i\phi_i)}{\vec r_l} = \opar{V_{\text{CBT}}}{\theta_{i-1}}\opar{\theta_{i-1}}{\vec r_l} + \opar{V_{\text{CBT}}}{\theta_i}\opar{\theta_i}{\vec r_l} + \opar{V_{\text{CBT}}}{\phi_i}\opar{\phi_i}{\vec r_l} \tag{4.70}\]
CBT基于无多重性的余弦形式, 因此它只在 \(0^{\circ}\) 左右对称. 为获得一个不对称的二面角分布(如在[\(-180^{\circ}:180^{\circ}\)]区间内只有一个最大值), 应该使用标准的扭转势, 如简谐角势或周期性的余弦势来代替CBT势. 然而, 这两种形式对于力的微分( \(1/\sin\phi\) )和珠子的直线排列( \(\theta_i\) 或 \(\theta_{i-1} = 0^{\circ}, 180^{\circ}\) )都不方便. 非 \(\cos\phi\) 势与 \(\sin^3\theta\) 因子的耦合并不能提高模拟的稳定性, 因为在某些情况下 \(\theta\) 和 \(\phi\) 同时为 \(180^{\circ}\). 在此步的积分是可能的(由于扭转势的抵消), 但下一步积分将是病态的( \(\theta\) 不是 \(180^{\circ}\) 而 \(\phi\) 非常接近 \(180^{\circ}\) ).
4.2.14 表格式键合相互作用
为了有充分的灵活性, 可通过用户提供的表格函数形式, 对键, 键角和二面角使用任何函数. 它们包括:
\[\alg V_b(r_{ij}) & =kf_n^b(r_{ij}) \tag{4.71} \\ V_a(\theta_{ijk}) &= k f_n^a(\theta_{ijk}) \tag{4.72} \\ V_d(\phi_{ijkl}) &= k f_n^d(\phi_{ijkl}) \tag{4.73} \ealg\]
其中, \(k\) 是以能量为单位的力常数, \(f\) 是三次样条函数;详细信息见6.10.1. 对每种相互作用, 在拓扑信息中指定力常数 \(k\) 和表格编号 \(n\). 有两种不同类型的键, 一种产生排除(类型8), 一种不产生排除(类型9). 详情见表5.5. 表格文件会被提供给mdrun程序. 表格文件名和下划线后, 加入字母“b”表示键, “a”表示角或“d”表示二面角和表格编号. 例如, 对一个 \(n = 0\) 的键(并使用默认的表格文件名), 将从文件table_b0.xvg中读取表格. 如拓扑信息(表5.5)中具体介绍的那样, 可简单地通过使用不同的 \(n\) 值提供多个表格, 并应用到恰当的键. 表格文件的格式是分别为 \(x, f(x), -f'(x)\) 的三列, 其中 \(x\) 必须是等间隔的. 拓扑信息的输入要求列于表5.5. 这些表格的设置如下:
键: \(x\) 是以纳米(nm)为单位的距离. 若模拟时距离超出表格长度, mdrun将显示错误消息并退出.
角度: \(x\) 是以度为单位的角度. 表格应从0开始直到并包括180度;导数以度为单位.
二面角: \(x\) 是以度为单位的二面角. 表格应从–180直到并包括180度, 使用IUPAC/IUB约定, 即零为顺式, 导数以度为单位.
4.3 限制
可以使用一些特殊的势能函数对体系的运动施加限制, 这样可以避免模拟中出现灾难性的偏差, 或是可以包含来自实验数据的知识. 无论哪种情况, 限制都不是力场的一部分, 并且所用参数的合理性也不重要. 提到GROMACS中实现的势能形式只是为了保持完整性. 在GROMACS中限制和约束所用的算法差异很大.
4.3.1 位置限制
位置限制用于将粒子限制在固定的参考位置 \(\bi R_i\). 在平衡过程中可利用它们来避免体系关键部分的位置产生剧烈的变化(例如, 当溶剂还未达到平衡时, 蛋白质会受到来自溶剂分子的很大的力, 这时就可以限制蛋白质中的一些运行). 位置限制的另一个应用是将粒子限制在围绕某个区域的壳层中, 以便对此区域进行细致的模拟. 壳层只是近似的, 因为它们缺少由壳层外面缺失粒子引起的适当的相互作用. 位置限制只是为了维持体系内部的完整性. 对球形壳层, 更好的做法是让力常数随半径变化, 由内部边界从零开始增加, 一直达到外部边界上的很大值. 但这一功能尚未在GROMACS中实现.
位置限制使用下面的势能形式
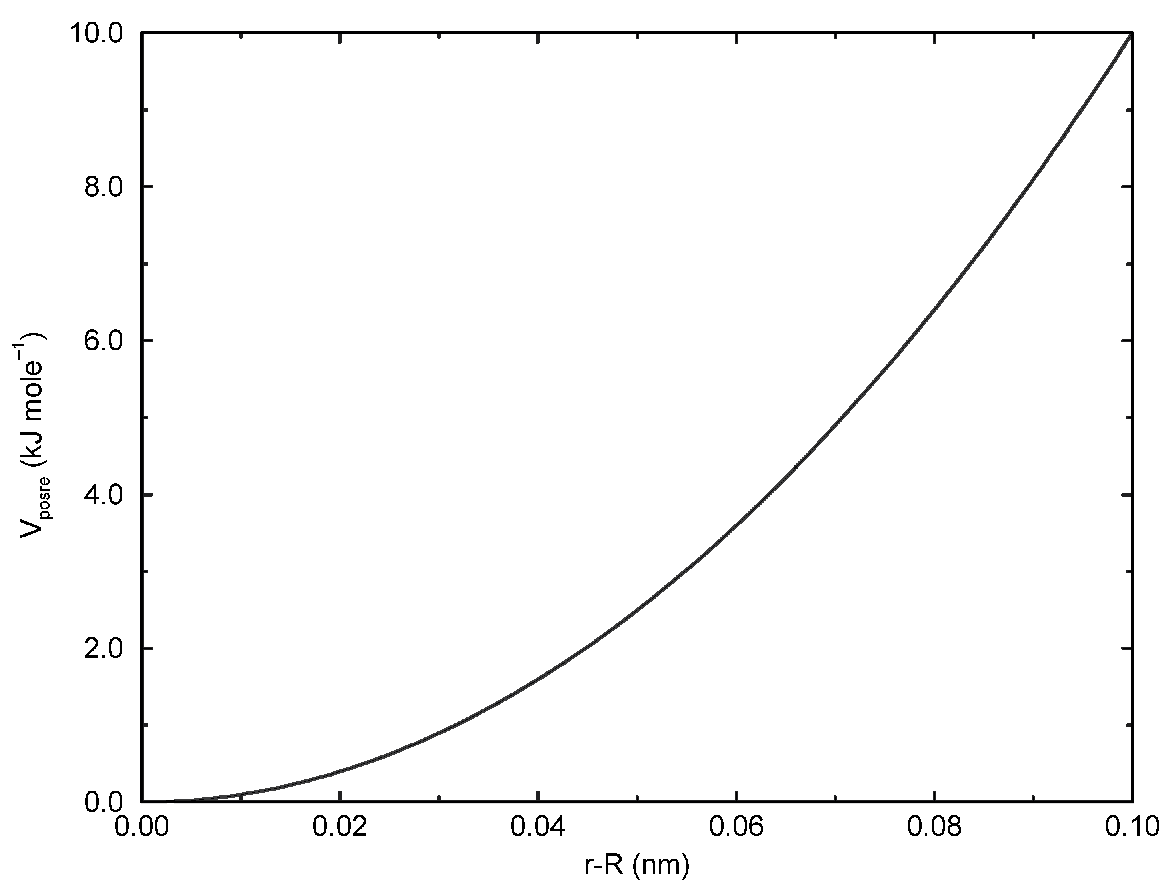
\[V_{pr}(\bi r_i)={1\over2} k_{pr} \left| \bi r_i-\bi R_i \right|^2 \tag{4.74}\]
此势能的图形见图4.14.
不失一般性, 可将势能改写为:
\[V_{pr}(\bi r_i)={1\over2}\left[ k_{pr}^x(x_i-X_i)^2 \hat x + k_{pr}^y (y_i-Y_i)^2 \hat y +k_{pr}^z (z_i-Z_i)^2 \hat z \right] \tag{4.75}\]
相应的力为
\[\alg F_i^x &=-k_{pr}^x (x_i-X_i) \\ F_i^y &=-k_{pr}^y (y_i-Y_i) \\ F_i^z &=-k_{pr}^z (z_i-Z_i) \\ \ealg\tag{4.76}\]
使用三个不同的力常数就可以在每个空间方向上打开或关闭位置限制, 这意味着原子可以简谐地限制于平面或直线上. 位置限制施加于指定的固定原子列表上, 这一列表通常使用pdb2gmx程序产生.
4.3.2 平底位置限制势
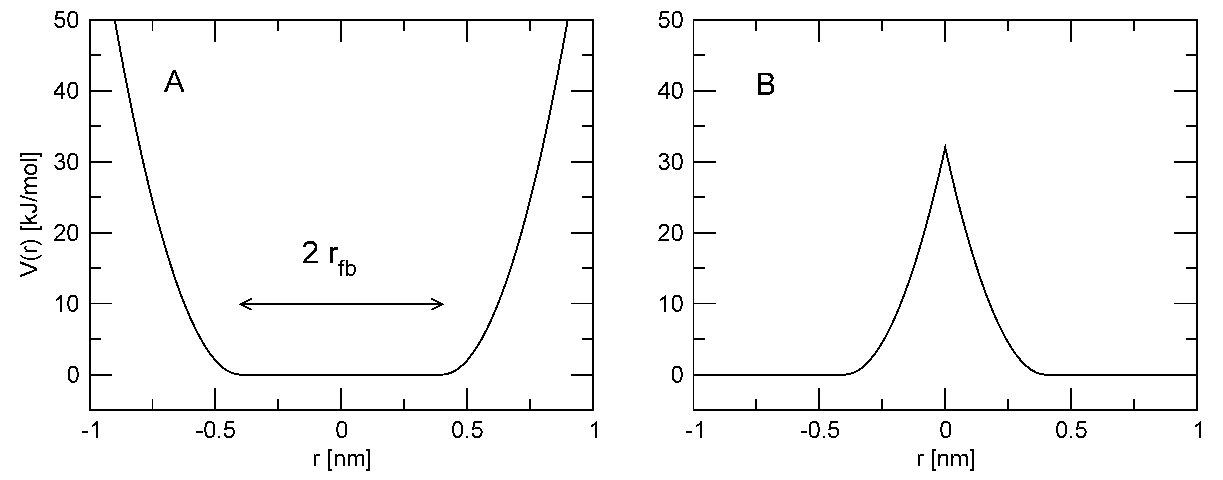
平底位置限制可用于将粒子限制在模拟体积的某一部分中. 在势能的平底区域中限制粒子不受力的作用, 但当粒子处于平底区域之外时会受到一个简谐力, 这个力会驱使粒子向平底区域运动. 对同一粒子可以同时施加常规的位置限制和平底的位置限制(但只用于相同的参考位置 \(\bi R_i\)). 平底位置限制使用下面的通用势能函数(图4.15 A):
\[V_\text{fb}(\bi r_i)={1\over2}k_\text{fb}[ d_g(\bi r_i; \bi R_i)-r_\text{fb}]^2 H[d_g(\bi r_i; \bi R_i)-r_\text{fb}] \tag{4.77}\]
其中 \(\bi R_i\) 为参考位置, \(r_\text{fb}\) 为平势离中心的距离, \(k_\text{fb}\) 为力常数, \(H\) 为Heaviside阶梯函数. 到参考位置的距离 \(d_g(\bi r_i; \bi R_i)\) 取决于平底势的几何构造 \(g\).
对平底势, GROMACS支持下面几种几何构造:
球 (\(g=1\)): 粒子被限制于给定半径的球中. 所受平底势的力指向球的中心, 距离的计算方法如下:
\[d_g(\bi r_i; \bi R_i)=\left| \bi r_i- \bi R_i \right| \tag{4.78}\]
圆柱 (\(g=2\)): 粒子被限制于给定半径的圆柱中. 圆柱的轴平行于 \(z\) 轴, 所受平底势的力指向圆柱的轴, 力的 \(z\) 分量为零. 距离的计算方法如下:
\[d_g(\bi r_i; \bi R_i)=\sqrt{(x_i-X_i)^2+(y_i-Y_i)^2} \tag{4.79}\]
层 (\(g=3, 4,5\)): 粒子限制于层中. 层由其厚度与法线定义, 法线可平行于 \(x\), \(y\) 或 \(z\) 轴, 作用力平行于层的法线. 距离的计算方法如下:
$$ d_g(\bi r_i; \bi R_i)=\left| x_i-X_i \right| \;\; 或 d_g(\bi r_i; \bi R_i)=\left| y_i-Y_i \right| \;\; d_g(\bi r_i; \bi R_i)=\left| z_i-Z_i \right| \tag{4.80}$$
对同一粒子可施加多个独立的, 具有不同几何构造的平底位置限制. 例如, 沿 \(z\) 方向同时施加圆柱和层限制可使粒子限制于一个圆盘中; 在 \(x\), \(y\), \(z\) 方向施加三个层限制可使粒子限制于立方体中.
此外, 可以反转限制区域和未限制区域, 这样得到的势能会使粒子处于 \(\bi R_i\), \(g\) 和 \(r_\text{fb}\) 定义的体积之 外. 在拓扑中定义负值的 \(r_\text{fb}\) 可启用此功能, 使用下面的势能:
\[V_\text{fb}^\text{inv}={1\over2}k_\text{fb}[ d_g(\bi r_i; \bi R_i)-\left|r_\text{fb}\right|]^2 H[-(d_g(\bi r_i; \bi R_i)-\left|r_\text{fb} \right|)] \tag{4.81}\]
4.3.3 角限制
角限制用于限制两对粒子间或一对粒子与 \(z\) 轴之间的角度. 所用的函数形式类似于恰当二面角, 对两对原子之间的角:
\[V_{ar}(\bi r_i, \bi r_j, \bi r_k, \bi r_l)=k_{ar}(1-\cos(n(\q-\q_0))), \;\; \q=\arccos\left( {\bi r_j-\bi r_i \over \| \bi r_j-\bi r_i \|} \cdot {\bi r_l-\bi r_k \over \|\bi r_l-\bi r_k \|} \right) \tag{4.82}\]
对一对原子与 \(z\) 轴之间的角:
\[V_{ar}(\bi r_i, \bi r_j)=k_{ar}(1-\cos(n(\q-\q_0))), \;\; \q =\arccos\left( {\bi r_j-\bi r_i \over \| \bi r_j-\bi r_i \|} \cdot \pmat 0 \\ 0 \\ 1 \epmat \right) \tag{4.83}\]
当不需要区分平行与反平行向量时, 多重性 \(n\) 可设为2. 当多重性为1时, 平衡角度 \(\q\) 应处于0度和180度之间; 当多重性为2时, \(\q\) 应处于0度和90度之间.
4.3.4 二面角限制
二面角限制用于限制由四个粒子定义的二面角, 如不当二面角(4.2.12节), 但使用了稍加修改的势能:
\[\phi'=(\phi-\phi_0)\; \text{MOD} \; 2\pi \tag{4.84}\]
其中 \(\f_0\) 为参考角度, 势能的定义为:
\[V_{dihr}(\f')=\begin{cases} {1\over2} k_{dihr}(\f'-\f_0-\D \f)^2 &\qquad 当\; \f' > \D \f \\ 0 &\qquad 当\; \f' \le \D \f \end{cases} \tag{4.85}\]
其中 \(\D \f\) 为用户定义的角度, \(k_{dihr}\) 为力常数. 注意, 在拓扑文件的输入中, 角度的单位为度, 力常数的单位为kJ/mol/rad2.
4.3.5 距离限制
当指定的一对原子之间的距离超过一个阈值时, 距离限制会给势能增加一个惩罚项. 它们通常用于施加来自实验的限制, 例如核磁共振(NMR, nuclear magnetic resonance)实验中对体系运动的限制. 因此, MD可用于NMR数据的结构精修. 在GROAMCS中, 有三种方式对原子对施加距离限制:
- 简单的简谐限制: 使用
[ bonds ]类型6. (见5.4节) - 分段线性/简谐限制:
[ bonds ]类型10. - 复杂的NMR距离限制, 可选的原子对, 时间和/或系综平均
下面将叙述后面两个选项.
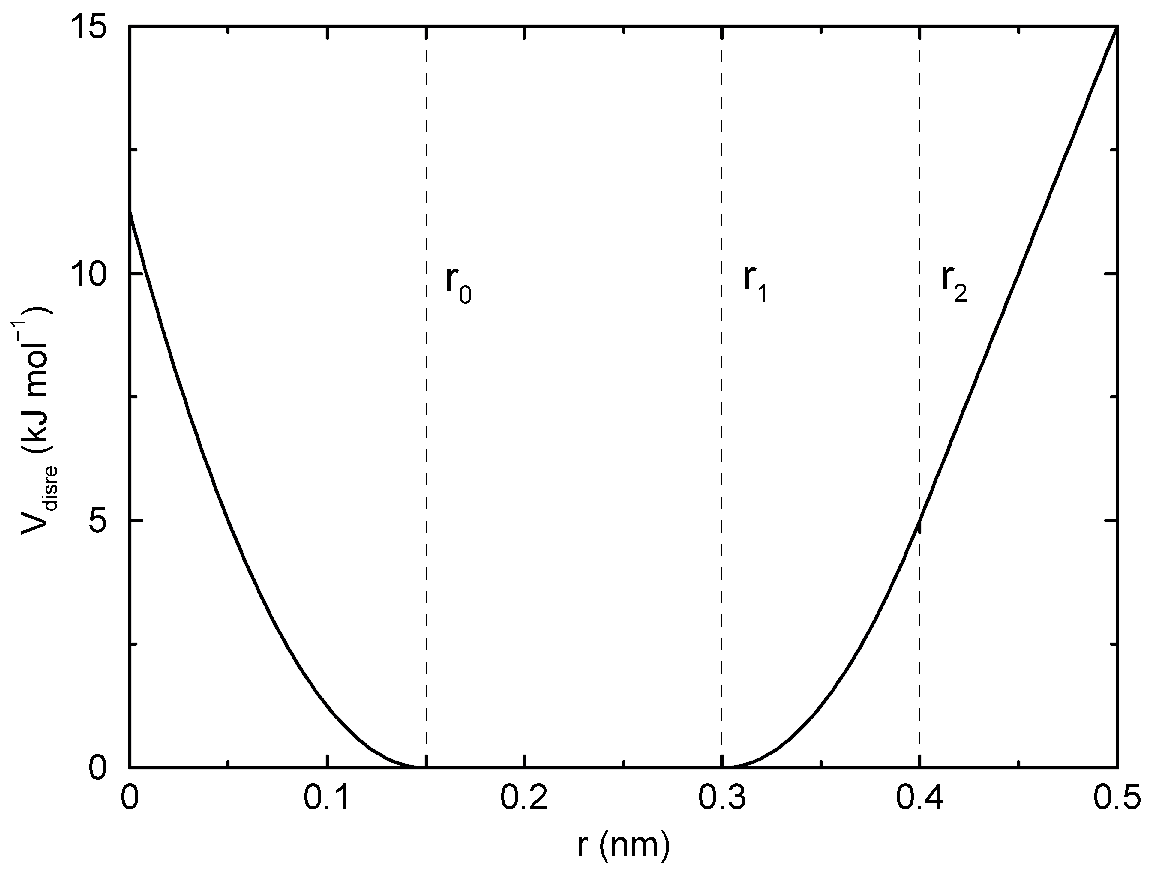
当低于指定的下界或处于指定的两个上界之间时, 距离限制的势能形式为二次; 当超过最大边界时, 势能为线性(见图4.16).
\[V_{dr}(r_{ij})= \begin{cases} {1\over2} k_{dr}(r_{ij}-r_0)^2 &\qquad 当\; & \phantom{r_0 \le{} } r_{ij} < r_0 \\ 0 &\qquad 当\; & r_0 \le r_{ij} < r_1 \\ {1\over2} k_{dr}(r_{ij}-r_1)^2 &\qquad 当\; & r_1 \le r_{ij} < r_0 \\ {1\over2} k_{dr}(r_2-r_1)(2r_{ij}-r_2-r_1) &\qquad 当\; & r_2 \le r_{ij} \end{cases} \tag{4.86}\]
相应的力为
\[F_i = \begin{cases} -k_{dr}(r_{ij}-r_0){\bi r_{ij} \over r_{ij} } &\qquad 当\; & \phantom{r_0 \le{} } r_{ij} < r_0 \\ 0 &\qquad 当\; & r_0 \le r_{ij} < r_1 \\ -k_{dr}(r_{ij}-r_1){\bi r_{ij} \over r_{ij} } &\qquad 当\; & r_1 \le r_{ij} < r_0 \\ -k_{dr}(r_2-r_1){\bi r_{ij} \over r_{ij} } &\qquad 当\; & r_2 \le r_{ij} \end{cases} \tag{4.87}\]
对不是由NMR数据导出的限制, 这个函数通常足够了, [ bonds ]类型10的段可用于在原子对之间施加独立的限制, 见5.7.1节. 对由NMR测量导出的限制, 可能需要更复杂的函数, 这可通过[ distance_restraints ]段提供, 具体将在下面论述.
时间平均
基于瞬时距离的距离限制可能会显著地减弱分子内的涨落. 采用 时间平均 的限制距离可以解决这个问题[91]. 时间平均的力为
\[F_i = \begin{cases} -k_{dr}^a (\bar r_{ij}-r_0){\bi r_{ij} \over r_{ij} } &\qquad 当\; & \phantom{r_0 \le{} } \bar r_{ij} < r_0 \\ 0 &\qquad 当\; & r_0 \le \bar r_{ij} < r_1 \\ -k_{dr}^a (\bar r_{ij}-r_1){\bi r_{ij} \over r_{ij} } &\qquad 当\; & r_1 \le \bar r_{ij} < r_0 \\ -k_{dr}^a (r_2-r_1){\bi r_{ij} \over r_{ij} } &\qquad 当\; & r_2 \le \bar r_{ij} \end{cases} \tag{4.88}\]
其中 \(\bar r_{ij}\) 由衰减时间为 \(\t\) 的指数运行平均给出:
\[\bar r_{ij}=\lt r_{ij}^{-3} \gt^{-1/3} \tag{4.89}\]
缓慢打开力常数 \(k_{dr}^a\), 以弥补模拟开始时缺少历史数据的问题:
\[k_{dr}^a=k_{dr} \left( 1-\exp\left(-{t\over\t}\right)\right) \tag{4.90}\]
由于时间平均, 我们无法再定义距离限制势了.
采用这种方式, 一个原子可以通过在两个位置之间移动 平均地 满足两个不兼容的距离限制. 例如围绕 \(\c\) 二面角旋转的氨基酸支链会因此接近其他各种基团. 这样的活动支链可导致多个NOE, 不能由单一结构满足.
mdrun程序计算时间平均距离的方法如下:
\[\begin{align} \overline{r^{-3} }_{ij}(0) &= r_{ij}(0)^{-3} \\ \overline{r^{-3} }_{ij}(t) &=\overline{r^{-3} }_{ij}(t-\D t) \exp\left(-{\D t \over \t}\right)+r_{ij}(t)^{-3}\left[1-\exp\left(-{\D t \over \t}\right)\right] \end{align} \tag{4.91}\]
当原子对处于边界之内时可能仍会受到力的作用, 因为时间平均的距离可能仍然超过了边界. 为防止质子彼此靠得太近, 可以使用一种混合的方法. 在这种方法中, 当瞬时距离处于边界之内时, 惩罚项为零, 在其他情况下惩罚项为瞬时偏离与时间平均偏离乘积的平方根:
\[\bi F_i=\begin{cases} k_{dr}^a \sqrt{(r_{ij}-r_0) (\bar r_{ij}-r_0)} {\bi r_{ij} \over r_{ij} } & 当\;\; r_{ij} < r_0 \;且\; \bar r_{ij} < r_0 \\ -k_{dr}^a \min\left(\sqrt{(r_{ij}-r_1)(\bar r_{ij}-r_1)}, r_2-r_1 \right) {\bi r_{ij} \over r_{ij} } & 当\;\; r_{ij}>r_1 \;且\; \bar r_{ij}>r_1 \\ 0 & 其他情况 \end{cases} \tag{4.92}\]
多对平均
根据实验数据, 有时不清楚是哪些原子对导致了单个NOE, 在其他一些情况下, 由于体系的对称性, 很显然地有多余一对的原子有贡献, 例如含有三个质子的甲基. 对这样一个基团, 不可能区分不同的质子, 因此当计算此甲基与其他质子(或一组质子)之间的距离时, 所有三个质子都要考虑. 由于磁共振的物理本性, NOE信号的强度与原子间距离的6次方成反比, 因此, 当联合原子对时, \(N\) 个限制的固定列表要放在一起, 表现出的“距离”为:
\[r_N(t)=\left[ \Sum_{n=1}^N \bar r_n(t)^{-6} \right]^{-1/6} \tag{4.93}\]
其中对 \(\bar r_n\) 我们可以使用 \(r_{ij}\) 或方程4.89. 瞬时距离和时间平均的距离 \(r_N\) 可以联合起来施加混合约束, 如上所述. 由于更多的质子对对相同的NOE信号有贡献, 其强度会增大, 由于是倒数加和, 累加的“距离”会小于距离的任何一个分量.
将力分布到原子对上时, 有两个选项. 对第一个守恒选项, 力定义为限制势对坐标的导数, 当不使用时间平均时, 得到的势能是守恒的. 分布到原子对上的力与 \(r^{-6}\) 成正比, 这意味着互相靠近的原子对比互相远离的原子对受到更大的力, 这可能导致分子“过于刚性”. 另一个选项是等力分配. 这种情况下, 每对原子受到的力为限制势对 \(r_N\) 导数的 \(1/N\). 这种方法的优势在于可以对更多的构型进行抽样, 但不守恒的力可能导致对质子的局部加热.
也可以使用多个(蛋白质)分子的 系综平均. 在这种情况下, 界限应当降低:
\[\begin{align} r_1 &= r_1*M^{-1/6} \\ r_2 &= r_2*M^{-1/6} \\ \end{align} \tag{4.94}\]
其中 \(M\) 为分子数. 当给出适当的选项时, GROMACS预处理器grompp可自动进行这些处理. 得到的“距离”用于计算标量力:
\[\bi F_i=\begin{cases} \begin{array}{cl} 0 & r_N < r_1 \\ k_{dr}(r_N-r_1) {r_{ij} \over r_{ij} } & r_1 \le r_N < r_2 \\ k_{dr}(r_2-r_1) {r_{ij} \over r_{ij} } & r_N \ge r_2 \end{array} \end{cases}\tag{4.95}\]
其中 \(i\), \(j\) 代表所有对NOE信号有贡献的原子对.
使用距离限制
在拓扑文件中可以将基于NOE数据的距离限制添加到分子定义中, 如下面的示例:
[ distance_restraints ]
; ai aj type index type' low up1 up2 fac
10 16 1 0 1 0.0 0.3 0.4 1.0
10 28 1 1 1 0.0 0.3 0.4 1.0
10 46 1 1 1 0.0 0.3 0.4 1.0
16 22 1 2 1 0.0 0.3 0.4 2.5
16 34 1 3 1 0.0 0.5 0.6 1.0
在这个例子中, 可以发现很多特性. ai列与aj列为限制粒子的原子编号. type列总是为1. 如在4.3.5节解释的那样, 多个距离可以对单个NOE信号有贡献. 在拓扑中, 这可使用index列指定. 在我们的例子中, 限制10–28和10–64的索引都是1, 因此它们会被同时处理. 一起处理的一个额外要求是几个限制必须位于连续的行中, 中间不能有其他限制. type'列通常为1, 但也可设为2, 以便不对距离限制进行时间平均与系综平均, 这适用于限制氢键. 列low, up1和up2分别为方程4.86中的 \(r_0\), \(r_1\) 和 \(r_2\) 值. 在一些情况下, 对一些限制使用不同的力常数可能有用, 这可通过fac列进行控制. 对每个限制, 参数文件中的力常数会乘上fac列中的值.
4.3.6 取向限制
本节论述在MD模拟中如何计算和限制向量间的取向, 如一些NMR实验中测量的. 这里论述的精修方法, 以及使用与不使用时间和系综平均对结果的影响已经发表[92].
理论
在NMR实验中, 当一个分子在溶剂中的翻滚并非完全各向同性时可测量矢量间的取向. 这种取向测量的两个例子是残基偶极耦合(两个原子核之间)或化学位移各向异性. 向量 \(\bi r\) 的可观测量可写为:
\[\d_i = {2\over3}\text{tr}(\mathbf{SD}_i) \tag{4.96}\]
其中 \(\mathbf S\) 为无量纲的分子序张量, 张量 \(\mathbf D_i\) 为
\[\mathbf D_i = {c_i \over \|\bi r_i\|^\alpha} \pmat 3xx-1 & 3xy & 3xz \\ 3xy & 3yy-1 & 3yz \\ 3xz & 3yz & 3zz-1 \\ \epmat \tag{4.97}\]
其中
\[x={r_{i,x} \over \|\bi r_i \|}, y={r_{i,y} \over \|\bi r_i \|}, z={r_{i,z} \over \|\bi r_i\|} \tag{4.98}\]
对一个偶极耦合 \(\bi r_i\) 为连接两个原子核间的向量, \(\a=3\), 常数 \(c_i\) 为:
\[c_i={\m_0 \over 4\p} \g_1^i \g_2^i {\hbar \over 4\p} \tag{4.99}\]
其中为 \(\g_1^i\) 和 \(\g_2^i\) 为两个核的旋磁比.
序张量是对称的, 迹为零. 使用旋转矩阵 \(\mathbf T\) 可将其变换为下面的形式:
\[\mathbf T^T \mathbf{ST}=s \pmat -{1\over2}(1-\h) & 0 & 0 \\ 0 & -{1\over2}(1+\h) & 0 \\ 0 & 0 & 1 \epmat \tag{4.100}\]
其中 \(-1 \le s \le 1\), \(0 \le \h \le 1\). \(s\) 称为序参数, \(\h\) 称为序张量 \(\mathbf S\) 的非对称性. 当分子在溶剂中的翻滚各向同性时, \(s\) 为零, 无法观测到取向效应, 因为所有的 \(\d_i\) 都是零.
模拟中取向的计算
由于下面将要解释的原因, \(\mathbf D\) 矩阵是相对于分子的参考取向计算的. 取向由旋转矩阵 \(\mathbf R\) 定义, 计算它时需要使用最小二乘方法将选定的一组原子的当前坐标拟合到参考构型, 参考构型为模拟的初始构型. 对后面将要处理的系综平均, 参考结构来自第一个子体系. \(\mathbf D_i^c\) 矩阵的计算方法为:
\[\mathbf D_i^c(t)= \mathbf R(t) \mathbf D_i(t) \mathbf R^T(t) \tag{4.101}\]
向量 \(i\) 的取向为:
\[\d_i^c(t)={2\over 3} \text{tr}( \mathbf S(t) \mathbf D_i^c(t)) \tag{4.102}\]
序张量 \(\mathbf S(t)\) 通常是未知的, 对它的一个合理选择是能够使计算与观测到的取向的(加权)平均方差最小的张量:
\[MSD(t)=\left( \Sum_{i=1}^N w_i\right)^{-1} \Sum_{i=1}^N w_i(\d_i^c(t)-\d_i^{exp})^2 \tag{4.103}\]
为正确地联合不同类型的测量, \(w_i\) 的单位应使得所有项都是无量纲的. 这意味着 \(w_i\) 单位的次数为 \(\d_i\) 单位的次数–2. 注意 使用常数因子缩放所有 \(w_i\) 并不影响序张量.
时间平均
由于张量 \(\mathbf D\) 随时间迅速涨落, 比能在实验中观测到的快得多, 在模拟中它们应当对时间进行平均. 然而, 在模拟中时间与分子数都是有限的, 通常不能得到对分子所有取向收敛的 \(\mathbf D_i\) 张量的平均值. 如果假定分子内 \(\bi r_i\) 向量平均取向的收敛比分子的翻滚时间快得多, 这一张量可以在随分子旋转的坐标系中进行平均, 如方程4.101所示. 时间平均的张量使用指数衰减记忆函数进行计算:
\[\mathbf D_i^a(t) = {\int_{u=t_0}^t \mathbf D_i^c(u)\exp\left(-{t-u \over \t}\right) \rmd u \over \int_{u=t_0}^t \exp\left(-{t-u \over \t}\right) \rmd u } \tag{4.104}\]
假定序张量 \(\mathbf S\) 的涨落慢于 \(\mathbf D_i\), 时间平均的取向为:
\[\d_i^a(t)={2\over3} \text{tr}(\mathbf S(t) \mathbf D_i^a(t)) \tag{4.105}\]
其中序张量 \(\mathbf S\) 使用表达式4.103进行计算, 但将其中的 \(\d_i^c(t)\) 替换为 \(\d_i^a(t)\).
限制
可以对模拟结构施加力进行限制, 施加的力正比于计算与实验取向之间差异. 无时间平均时, 恰当的势能可定义为:
\[V={1\over2} k\Sum_{i=1}^N w_i(\d_i^c(t)-\d_i^{exp})^2 \tag{4.106}\]
其中 \(k\) 的单位为能量单位, 这样限制 \(i\) 的有效力常数为 \(kw_i\). 力是势能 \(V\) 的梯度的负值. 作用于向量 \(\bi r_i\) 上的力 \(\bi F_i\) 为:
\[\alg \bi F_i(t) &= -{\rmd V \over \rmd {\bi r_i} } \\ &= -k w_i(\d_i^c(t)-\d_i^{exp}) {\rmd {\d_i(t)} \over \rmd {\bi r_i} } \\ &= -k w_i(\d_i^c(t)-\d_i^{exp}) {2 c_i \over \|\bi r\|^{2+\a} } \left(2\mathbf R^T \mathbf S \mathbf R \bi r_i - {2 +\a \over \|\bi r\|^2} \text{tr}(R^T \mathbf S \mathbf R \bi r_i \bi r_i^T) \bi r_i \right) \ealg\]
系综平均
系综平均可通过模拟一个具有 \(M\) 个子体系的体系来实现, 其中每个子体系包含了完全相同的取向限制. 体系只通过取向限制势进行相互作用:
\[V=M{1\over2} k \Sum_{i=1}^N w_i < \d_i^c(t)-\d_i^{exp}>^2 \tag{4.107}\]
子体系 \(m\) 中向量 \(\bi r_{i,m}\) 上的力为:
\[\bi F_{i,m}(t)=-{\rmd V \over \rmd {\bi r_{i,m} } }=-k w_i < \d_i^c(t)-\d_i^{exp} > {\rmd {\d_{i,m}^c(t)} \over \rmd {\bi r_{i,m} } } \tag{4.108}\]
时间平均
当使用时间平均时, 无法定义势能. 但我们仍可以定义一个量, 它粗略地表示了限制的能量:
\[V=M{1\over2} k^a \Sum_{i=1}^N w_i < \d_i^a(t)-\d_i^{exp}>^2 \tag{4.109}\]
缓慢打开力常数 \(k^a\), 以弥补时间接近 \(t_0\) 时缺少历史数据的问题. 它精确地正比于已积累的平均量:
\[k^a =k {1\over \t} \int_{u=t_0}^t \exp\left(-{t-u \over \t}\right) \rmd u \tag{4.110}\]
真正关键的是力的定义, 它正比于时间平均与瞬时偏差乘积的平方根. 只使用时间平均的偏差会导致大的振荡. 力的计算方式如下:
\[\bi F_{i,m}(t)= \begin{cases} 0 &当\; ab \le 0 \\ k^a w_i {a \over |a|} \sqrt{ab} {\rmd {\d_{i,m}^c(t)} \over \rmd {\bi r_{i,m} } } &当\; ab > 0 \\ \end{cases} \tag{4.111} \\ a =< \d_i^a(t)-\d_i^{exp} >\\ b =< \d_i^c(t)-\d_i^{exp} >\]
使用取向限制
在拓扑文件的[ orientation_restraints ]段中可以将取向限制添加到分子的定义中. 这里我们给出一个示例段, 包含了五个N-H残基的偶极耦合限制:
[ orientation_restraints ]
; ai aj type exp. label alpha const. obs. weight
; Hz nm^3 Hz Hz^-2
31 32 1 1 3 3 6.083 -6.73 1.0
43 44 1 1 4 3 6.083 -7.87 1.0
55 56 1 1 5 3 6.083 -7.13 1.0
65 66 1 1 6 3 6.083 -2.57 1.0
73 74 1 1 7 3 6.083 -2.10 1.0
观测量的单位为Hz, 但也可以选择任何其他单位. ai列与aj列为限制粒子的原子编号. type列总是为1. exp.列代表实验编号, 从1开始. 对每次实验, 会优化单独的序张量 \(\mathbf S\). 对每个限制, 其标签应为大于零的唯一数字. alpha列包含了方程4.97中用于计算取向的次数 \(\a\). const.列包含相同方程中使用的常数 \(c_i\). 这些常数的单位应为观测量乘上 \(\text{nm}^\a\). obs.列包含了观测量, 单位任意. 最后一列包含权重 \(w_i\), 其单位为观测量单位平方的倒数.
取向限制的一些参数可在grompp.mdp文件中设定. 不同力常数, 平均时间和系综平均对结果的影响, 请参考论文[92].
4.4 极化
GROMACS可处理极化, 采用的方法是将壳层(Drude)粒子附着到原子和/或虚拟位点上. 然后在每个时间步对壳层粒子的能量进行最小化, 以维持体系处于Born-Oppenheimer势能面上.
4.4.1 简单极化
只是平衡距离为零的简谐势.
4.4.2 水极化
用于水的特殊势能, 允许单个壳层粒子的各向异性极化[43].
4.4.3 Thole极化
基于Thole的早期工作[93], Roux及其合作者实现了对乙醇这样分子的势能[94, 95, 96]. 在这些分子中, 壳层粒子之间存在分子内的相互作用, 然而, 必须对这些相互作用进行屏蔽, 因为完全的库仑作用太强了. 两个壳层粒子 \(i\) 和 \(j\) 之间的势能为:
\[V_{thole}={q_i q_j \over r_{ij} } \left[ 1-\left(1+{\bar r_{ij}\over 2}\right) \exp(-\bar r_{ij}) \right] \tag{4.112}\]
注意, 在Noskov等人的文章中[96], 方程1有一个符号错误:
\[\bar r_{ij}=a {r_{ij} \over (\a_i \a_j)^{1/6} } \tag{4.113}\]
其中 \(a\) 为一个魔术常数(无量纲), 通常取2.6[96]; \(\a_i\) 和 \(\a_j\) 分别为壳层粒子的极化率.
4.5 自由能相互作用
本节叙述自由能计算中, 势能对 \(\l\) 的依赖关系(见3.12节). 所有常见的势能类型与约束类型都可以在状态A(\(\l=0\))和状态B(\(\l=1\))之间光滑地进行插值, 反之亦然. 所有键合相互作用都利用对相互作用参数的线性插值进行插值, 非键相互作用可以使用线性插值或软核相互作用.
从GROMACS4.6开始, \(\l\) 是一个向量, 允许自由能转变的不同分量以不同速率进行. 库仑, Lennard-Jones, 键合和限制项都可以使用.mdp文件中的选项独立地进行控制.
简谐势
这里给出的例子针对键势能, 在GROMACS中使用的是简谐势. 然而, 这些方程也同样适用于键角势与不当二面角势.
\(\alg V_b &= {1\over 2} \left[ (1-\l) k_b^A+\l k_b^B \right] \left[b-(1-\l)b_0^A-\l b_0^B \right]^2 \tag{4.114} \\ \opar{V_B}{\l} &= {1\over 2} (k_b^B-k_b^A)\left[ b-(1-\l)b_0^A+\l b_0^B \right]^2 + \\ & \qquad (b_0^A-b_0^B) \left[ b-(1-\l)b_0^A-\l b_0^B \right] \left[ (1-\l) k_b^A+\l k_b^B \right] \tag{4.115} \ealg\)
GROMOS–96键和键角
对四次键伸缩势与基于余弦的键角势, 通过对力常数与平衡位置的线性插值进行插值, 这里就不给出相应的公式了.
恰当二面角
对恰当二面角, 这些方程更复杂一些:
\(\alg V_d &= \left[ (1-\l) k_d^A+\l k_d^B \right] \left(1+\cos\left[n_\f \f -(1-\l)\f_s^A-\l \f_s^B \right] \right) \tag{4.116} \\ \opar{V_d}{\l} &= (k_d^B-k_d^A) \left(1+\cos\left[n_\f \f-(1-\l)b_s^A-\l \f_s^B \right] \right) + \\ & \quad (\f_s^B-\f_s^A) \left[ (1-\l)k_d^A-\l k_d^B \right] \sin\left[n_\f \f-(1-\l) \f_s^A-\l \f_s^B \right] \tag{4.117} \ealg\)
注意, 多重性 \(n_\f\) 不能参数化, 因为函数在 \([0,2\p]\) 区间内应当保持周期性.
表格键相互作用
对表格键合相互作用, 只对力常数进行插值:
\(\alg V &= \left( (1-\l)k^A+\l k^B \right)f \tag{4.118} \\ \opar V \l &= (k^B-k^A)f \tag{4.119} \ealg\)
库仑相互作用
对两个粒子之间的库仑相互作用, 粒子电荷随 \(\l\) 的变化关系如下:
\(\alg V_c &= {f \over \ve_{rf} r_{ij} } \left[ (1-\l) q_i^A q_j^A +\l q_i^B q_j^B \right] \tag{4.120} \\ \opar {V_c} \l &= {f \over \ve_{rf} r_{ij} } \left[-q_i^A q_j^A +\l q_i^B q_j^B \right] \tag{4.121} \ealg\)
其中 \(f={1\over 4\p\ve_0}= 138.935\ 485\)(见第二章).
反应场库仑相互作用
对两个粒子间包含反应场的库仑相互作用, 粒子电荷随 \(\l\) 的变化关系如下:
\(\alg V_c &= f\left[{1\over r_{ij} }+k_{rf} r_{ij}^2-c_{rf} \right] \left[(1-\l) q_i^A q_j^A +\l q_i^B q_j^B \right] \tag{4.122} \\ \opar {V_c} \l &= f\left[ {1\over r_{ij} } +k_{rf}r_{ij}^2 -c_{rf} \right] \left[-q_i^A q_j^A + q_i^B q_j^B \right] \tag{4.123} \ealg\)
注意, 常数 \(k_{rf}\) 和 \(c_{rf}\) 是利用介质的介电常数 \(\ve_{rf}\) 进行定义的(参看4.1.4节).
Lennard-Jones相互作用
对两个粒子间的Lennard-Jones相互作用, 原子类型 随 \(\l\) 的变化关系可写为:
\(\alg V_{LJ} &= {(1-\l) C_{12}^A + \l C_{12}^B \over r_{ij}^{12} } - {(1-\l)C_6^A+\l C_6^B \over r_{ij}^6} \tag{1.124} \\ \opar{V_{LJ} } \l &= {C_{12}^B - C_{12}^A \over r_{ij}^{12} } - {C_6^B-C_6^A \over r_{ij}^6} \tag{1.125} \ealg\)
应当指出, 从状态A到状态B的途径也可以利用 \(\s\) 和 \(\e\) 进行表达(见方程4.5). 看起来改变力场参数 \(\s\) 和 \(\e\) 而不是导出参数 \(C_{12}\), \(C_6\) 物理上可能更合理, 但在参数空间中这两种途径之间的差别并不大, 而且自由能自身与途径无关, 因此我们使用了上面的简单公式.
动能
当粒子的质量改变时, 动能对自由能也有贡献(注意, 我们不能将动量 \(\bi p\) 写为 \(m \bi v\), 因为那样会导致 \(\opar {E_k} \l\) 的符号错误[97]):
\(\alg E_k &= {1\over2} {\bi p^2 \over (1-\l)m^A+\l m^B } \tag{4.126} \\ \opar{E_k} \l &= -{1\over 2} {\bi p^2(m^B-m^A) \over((1-\l)m^A+\l m^B)^2 } \tag{4.127} \ealg\)
求导后, 可以 代入 \(\bi p=m \bi v\), 得到
\[\opar {E_k} \l = -{1\over2} \bi v^2 (m^B-m^A) \tag{4.128}\]
约束
约束是哈密顿量正式的一部分, 因此对自由能也有贡献. 在GROMACS中这可以使用LINCS或SHAKE算法进行计算. 如果我们有一些约束方程 \(g_k\):
\[g_k=\bi r_k-d_k \tag{4.129}\]
其中 \(\bi r_k\) 为两粒子间的距离向量, \(d_k\) 为两粒子间的约束距离. 利用距离与 \(\l\) 的关系, 我们可将方程改写为
\[g_k=\bi r_k-\left((1-\l)d_k^A+\l d_k^B \right) \tag{4.130}\]
使用Lagrange乘子, \(C_\l\) 对哈密顿量的贡献
\(\alg C_\l &= \Sum_k \l_k g_k \tag{4.131} \\ \opar {C_\l} \l &= \Sum_k \l_k \left(d_k^B-d_k^A \right) \tag{4.132} \ealg\)
4.5.1 软核相互作用
在自由能计算中, 当有粒子出现或消失时, 对Lennard-Jones势和库仑势使用方程4.125和4.123中的简单线性插值, 可能收敛很差. 当粒子几乎消失或接近消失时(\(\l\) 接近0或1), 相互作用能会变得足够弱, 粒子彼此可能非常接近, 致使得到的 \(\partial V/\partial \l\) 值的涨落非常大(因为简单线性插值同时取决于 \(\l\) 两端点的值).
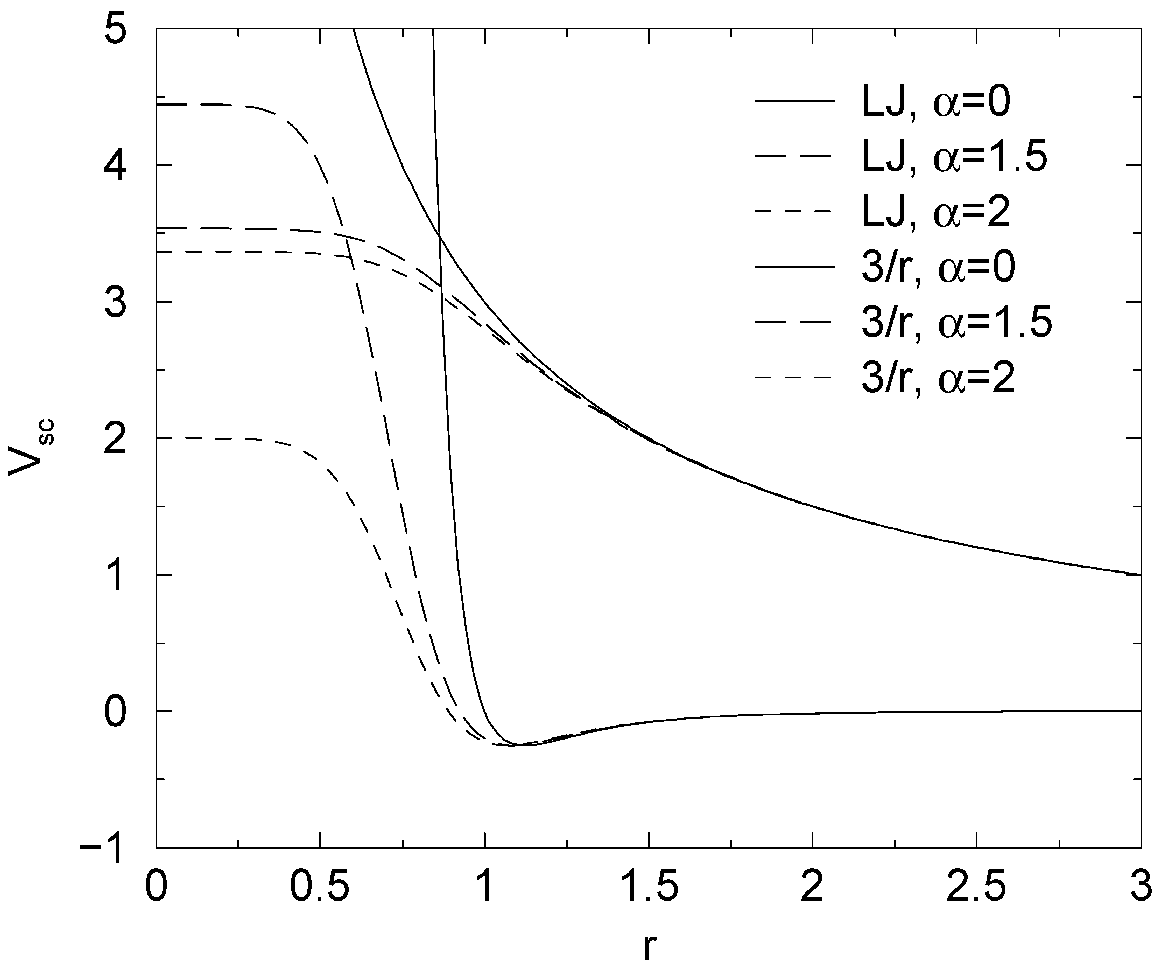
为避免这些问题, 需要去除势能的奇异性. 这可以通过利用“软核”势修改常规的Lennard-Jones势和库仑势来实现, 软核势限制了 \(\l\) 值处于0和1之间的能量和力, 但不改变 \(\l=0\) 或1时的势能和力.
在GROMACS中, 软核势是常规势能的偏移, 因此势能及其导数的奇点完全不可能出现在 \(r=0\) 处:
\(\alg V_{sc} &= (1-\l)V^A(r_A) + \l V^B(r_B) \tag{4.133} \\ r_A &= \left(\a \s_A^6 \l^p+r^6 \right)^{1\over6} \tag{4.134} \\ r_B &= \left(\a \s_B^6(1-\l)^p+r^6 \right)^{1\over6} \tag{4.135} \\ \ealg\)
其中 \(V^A\) 和 \(V^B\) 分别为状态A(\(\l=0\))和状态B(\(\l=1\))中正常的“硬核”Van der Waals势或静电势, \(\a\) 为软核参数(在.mdp文件中利用sc_alpha进行设置), \(p\) 为软核 \(\l\) 的次数(使用sc_power进行设置), \(\s\) 为相互作用半径, 其值为 \((C_{12}/C_6)^{1/6}\), 当 \(C_6\) 或 \(C_{12}\) 为零时, \(\s\) 是一个输入参数(由sc_sigma设置).
对中等大小的 \(\l\), \(r_A\) 和 \(r_B\) 对 \(r>\a^{1/6}\s\) 范围的势能改变很小, 对更小的 \(r\) 它们可使软核相互作用快速地变为一个常数(图4.17). 相应的力为:
\[F_{sc}(r) = -\opar { V_{sc}(r)} r =(1-\l)F^A(r_A)\left({r\over r_A}\right)^5 +\l F^B(r_B) \left({r\over r_B}\right)^5 \tag{4.136}\]
其中 \(F^A\) 和 \(F^B\) 为“硬核”力. 对自由能导数的贡献为:
\[\alg \opar{V_{sc}(r)} \l &= V^B(r_B)-V^A(r_A)+(1-\l) \opar{V^A(r_A)} {r_A} \opar{r_A} \l + \l \opar{V^B(r_B)}{r_B} \opar {r_B} \l \\ &= V^B(r_B)-V^A(r_A) + \\ &\quad {p\a \over 6} \left[ \l F^B(r_B) r_B^{-5} \s_B^6(1-\l)^{p-1}-(1-\l)F^A(r_A) r_A^{-5} \s_A^6 \l^{p-1} \right] \tag{4.137} \ealg\]
GROMACS原始的Lennard-Jones软核函数使用的 \(p=2\), 但 \(p=1\) 给出的 \(\partial H/\partial \l\) 曲线更光滑.
另一个应当考虑的事情是, 软核对那些无Lennard-Jones相互作用的氢原子的影响. 它们的软核参数 \(\s\) 使用.mdp文件中的sc-sigma选项设置. 对 \(p=1\), 当 \(\l=0\) 和/或1时, 或对 \(p=2\), 当 \(\l\) 接近0或1时, 这些氢原子会使 \(\partial H/\partial \l\) 曲线产生峰值. 降低sc-sigma的值可减小这种效应, 但相对于软核状态中其他的相互作用, 这种做法会增加与氢原子的相互作用.
当选择软核势时(设置sc-alpha>0), 依次打开和关闭库仑和Lennard-Jones, 然后线性地关闭库仑相互作用, 而不使用软核相互作用, 在大多数情况下, 这种做法的统计噪声会更小. 可将mdp选项sc-coul设为yes来取消这种行为. 此外, 软核相互作用只用于当A或B状态具有零相互作用的情况. 若A和B状态都具有非零的相互作用势, 会使用上文所说的线性缩放方法. 当同时关闭库仑和Lennard-Jones相互作用时, 会使用软核势, 并引入或删除一个氢原子, 将sigma参数设置为sc-sigma-min, 其自身默认值为sc-sigma-default.
最近, 有人推导了软核方法一个新公式, 与上面所述的标准软核途径相比, 在大多数情况下, 它给出的统计方差更低[99, 100].
\(\alg V_{sc}(r) &= (1-\l) v^A(r_A)+\l V^B(r_B) \tag{4.138} \\ r_A &= \left( \a \s_A^{48} \l^p + r^{48} \right)^{1\over 48} \tag{4.139} \\ r_B &= \left( \a \s_B^{48}(1-\l)^p + r^{48} \right)^{1\over 48} \tag{4.140} \ealg\)
GROMACS也实现了这种“1–1–48”途径. 注意对这种途径, 软核参数应满足 \(0.001 \lt \a \lt 0.003\), 而不是 \(\a \approx 0.5\).
4.6 方法
4.6.1 排除和1–4相互作用
一个分子链中互相邻近的原子, 即那些以共价键结合, 或者通过一个或两个原子相连的原子分别被称为 第一相邻原子, 第二相邻原子 和 第三相邻原子(见图4.18). 由于原子 i 与原子 i+1 和 i+2 之间的相互作用主要是量子力学的, 因此不能用Lennard-Jones势进行描述. 作为替代, 我们假定这些相互作用可以利用简谐键项或约束(i, i+1)和简谐键角项(i, i+2)进行充分的描述. 因此, 将第一和第二相邻原子(原子 i+1, i+2) 从原子 i 的Lennard-Jones相互作用列表中 排除. 原子 i+1, i+2 被称为原子 i 的排除原子.
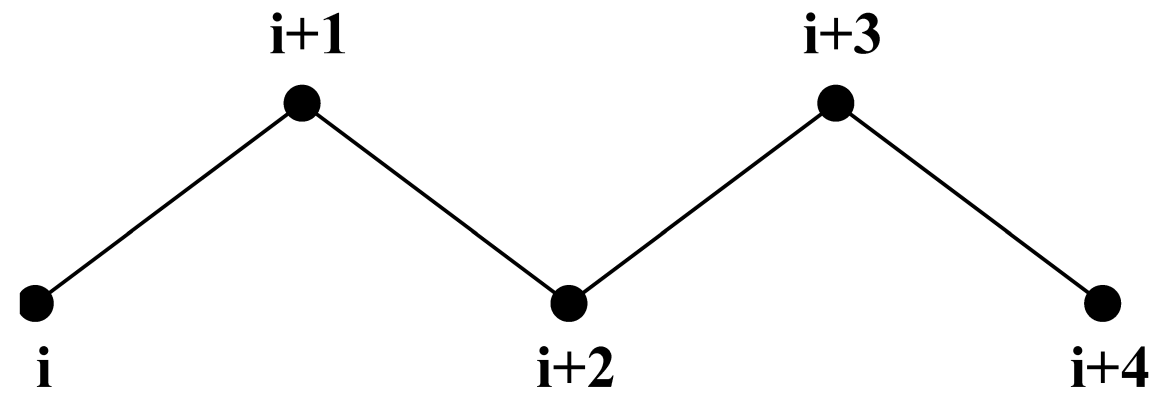
对第三个相邻原子, 正常的Lennard-Jones排斥作用有时仍然过强, 这意味着当将其应用于分子时, 分子会因内部张力发生变形或者破碎, 对顺式构象的碳-碳相互作用情况尤其如此(如顺丁烷). 因此, 对一些这样的相互作用, , 其Lennard-Jones排斥在GROMACS力场中被减弱了, 这是通过维持一个单独的1–4作用列表和正常的Lennard-Jones参数列表实现的. 在其他力场中, 如OPLS[101], 标准的Lennard-Jones参数减少为原来的1/2, 但在这种情况下, 也会对色散(r-6)和库伦相互作用进行相应的缩放. GROMACS可以使用这些方法中的任何一种.
4.6.2 电荷组
原则上, MD中力的计算复杂度是 \(O(N^2)\). 因此, 对非键力(NBF, non-bonded force)的计算我们使用了截断: 只有彼此间的距离在一定范围内的粒子才会相互作用. 这将NBF计算的复杂度减少为 \(O(N)\)(典型的是 \(100N\) 到 \(200N\)), 但同时也引入了误差. 在大多数情况下, 误差是可以接受的, 除了使用截断会导致电荷产生时. 在这种情况下, 应该考虑使用GROMACS提供的格点加和方法.
让我们考虑水分子与另一个原子的相互作用. 如果在原子-原子的基础上使用普通的截断, 我们可能包括了原子和氧之间的相互作用(电荷为–0.82), 而没有包括质子的平衡电荷, 结果将导致体系中出现了一个很大的偶极矩. 因此, 我们必须保证原子组的总电荷为0. 这些组被称为 电荷组. 注意, 如果对长程静电相互作用使用了好的处理方法(如粒子网格Ewald方法, 见4.8.2节), 就不需要将电荷组维持在一起.
4.6.3 组方案中截断的处理
GROMACS在处理截断时相当灵活, 这意味有大量的参数可供设置. 这些参数在grommp的输入文件中设置. 影响到截断相互作用的参数有两类: 你可以选择在每种情况下使用哪种相互作用, 在邻区搜索中使用哪种截断.
对于库伦和范德华相互作用有相应的相互作用类型选择词(vdwtype和coulombtype项)和两个参数, 一共六个非键相互作用参数. 参见7.3节对这些参数的完整描述.
邻区搜索(NS, neighbor searching)可使用单程或双程方法进行. 由于前者只是后者的特例, 我们将只讨论更一般的双程方法. 在这种情况下, NS会使用两个半径: rlist和max(rcoulomb,rvdw). 通常每10个时间步或每20 fs(参数nstlist)重新构建一次邻区列表. 在邻区列表中, 会存储所有落在rlist范围内的相互作用对. 此外, 对于没有落在rlist范围内但落在max(rcoulomb,rvdw)范围内的粒子对, 它们之间的相互作用在邻区搜索过程中也会被计算. 力和能量会分开存储, 在连续的NS之间, 在每个积分步会将它们添加到短程力中. 如果rlist = max(rcoulomb,rvdw), 生成邻区列表时不会计算力. 根据短程力与长程力的总和来计算维里, 这意味着在非NS步中维里可能有稍微的不对称. 当使用混合精度的mdrun时, 维里几乎总是不对称的, 因为非对角元素与加和中的每个元素相差不大. 在大多数情况下, 这些都不是真正的问题, 因为维里的涨落可以比平均值大两个数量级.
除了普通截断, 由于需要使用电荷组, 表4.2中所有的相互作用函数都要求使用比为其形式指定的 \(r_c\) 更大的半径进行邻区搜索. 额外半径的典型值是0.25 nm(粗略地等于电荷组中两原子之间的最大距离加上电荷组在邻区列表更新中可扩散的距离).
| 类型 | 参数 | ||
|---|---|---|---|
| 库仑 | 普通截断 | \(r_c, \ve_r\) | |
| 反应场 | \(r_c, \ve_{rf}\) | ||
| 移位函数 | \(r_1, r_c, \ve_r\) | ||
| 切换函数 | \(r_1, r_c, \ve_r\) | ||
| VdW | 普通截断 | \(r_c\) | |
| 移位函数 | \(r_1, r_c\) | ||
| 切换函数 | \(r_1, r_c\) | ||
4.7 虚拟相互作用位点
在GROMACS中可以各种方式使用虚拟相互作用位点(在GROMACS 3.3以前的版本中被称为哑原子). 我们将虚拟位点的位置 \(\bi r_s\) 写为其他粒子位置 \(\bi r_i\) 的函数: \(\bi r_s = f(\bi r_1..\bi r_n)\), 这样就可以在力的计算中使用虚拟位点了, 它可能带有电荷或者涉及其他相互作用. 作用于虚拟位点上的力必须以一种自洽的方式被重新分配到有质量的粒子上. 在参考文献[102]中可以找到一个较好的方. 我们可以将势能写为:
\[V = V (\bi r_s, \bi r_1,...,\bi r_n) = V^*(\bi r_1,...,\bi r_n) \tag{4.141}\]
作用于粒子 \(i\) 上的力为:
\[\bi F_i = - \opar{V^*}{\bi r_i} = -\opar{V}{\bi r_i}-\opar{V}{\bi r_s} \opar{\bi r_s}{\bi r_i} = \bi F_i^{direct} + \bi F_i' \tag{4.142}\]
第一项是正常的力, 第二项是因虚拟位点引起的作用于粒子 \(i\) 上的力, 可以将它写为张量形式:
\[\bi F_i'=\bmat \opar{x_s}{x_i} & \opar{y_s}{x_i} & \opar{z_s}{x_i} \\ \opar{x_s}{y_i} & \opar{y_s}{y_i} & \opar{z_s}{y_i} \\ \opar{x_s}{z_i} & \opar{y_s}{z_i} & \opar{z_s}{z_i} \\ \ebmat \bi F_s \tag{4.143}\]
其中 \(\bi F_s\) 为虚拟位点上的力, \(x_s\), \(y_s\) 和 \(z_s\) 为虚拟位点的坐标. 这样, 合力和总的力矩都是守恒的.

当使用虚拟位点时, 维里的计算(方程3.24)并不简单. 由于维里涉及到所有原子的加和(而不仅虚拟位点), 在计算维里 之前, 虚拟位点上的力必须被重新分配到原子上(使用方程4.143). 在一些特殊的情况下, 原子上的力可以写为虚拟位点上的力的线性组合(下面的类型2和类型3), 计算维里时是否重新分配力没有区别. 然而, 一般情况下, 应该首先进行力的重新分配.
在GROMACS中, 从周围原子构建虚拟位点的方法共有六种, 我们按构建原子的数目对其进行分类. 注意, 所有提到的位点类型都可以利用类型3fd(归一化的, 平面内)和3out(为归一化, 平面外)进行构造. 然而, 涉及到的计算量按列表顺序迅速增大, 因此我们强烈推荐使用第一个适合的虚拟位点类型, 只要它能满足一定的目的. 图4.19给出了6种可用的虚拟位点构建方式. 概念上最简单的构建类型是线性组合:
\[\bi r_s = \Sum_{i=1}^N \w_i \bi r_i \tag{4.144}\]
使用相同的权重分重新分配力:
\[\bi F_i'=\w_i \bi F_s \tag{4.145}\]
GROMACS支持的虚拟位点类型将在下面列出. 虚拟位点中的构建原子也可以是虚拟位点自身, 但仅当它们处于列表中的较高位置时, 即虚拟位点可以利用比虚拟位点简单的“粒子”进行构建.
2. 两个原子的线性组合(图4.19 2):
\[\w_i = 1 - a, \w_j = a \tag{4.146}\]
这种情况下虚拟位点位于通过原子 \(i\) 和 \(j\) 的线上.
3. 三个原子的线性组合(图4.19 3):
\[\w_i = 1 - a - b, \w_j = a, \w_k = b \tag{4.147}\]
这种情况下虚拟位点位于另外三个原子构成的平面上.
3fd. 在三个原子构成的平面中, 具有固定的距离(图4.19 3fd):
\[\bi r_s=\bi r_i+b {\bi r_{ij}+a \bi r_{jk} \over \abs{\bi r_{ij}+a\bi r_{jk}} } \tag{4.148}\]
这种情况下虚拟位点位于其他三个粒子所构成的平面中, 与原子 \(i\) 的距离为 \(|b|\). 由虚拟位点上的力引起的粒子 \(i\), \(j\) 和 \(k\) 上的力为:
\(\alg \bi F_i' &= \bi F_s - \g(\bi F_s-\bi p)& \\ \bi F_j' &= (1-a) \g(\bi F_s-\bi p)& \\ \bi F_k' &= a\g(\bi F_s-\bi p)& \\ \g & = {b \over |\bi r_{ij}+a\bi r_{jk} |} \\ \bi p &= {\bi r_{is} \cdot \bi F_s \over \bi r_{is} \cdot \bi r_{is} } \bi r_{is} \ealg \tag{4.149}\)
3fad. 在三个原子所构成的平面中, 具有固定的角度和距离(图 4.19 3fad):
\(\alg \bi r_s &=\bi r_i+d\cos\q{\bi r_{ij} \over |\bi r_{ij}|} +d\cos\q{\bi r_\bot \over |\bi r_\bot|} \\ \bi r_\bot &= \bi r_{jk}-{\bi r_{ij} \cdot \bi r_{jk} \over \bi r_{ij} \cdot \bi r_{ij} } \bi r_{ij} \ealg \tag{4.150}\)
这种情况下虚拟位点位于其他三个粒子所构成的平面中, 与原子 \(i\) 的距离为 \(|d|\), 与 \(\bi r_{ij}\) 所成的角度为 \(\a\). 原子 \(k\) 定义了平面以及角度的方向. 注意, 在这种情况下必须明确指定 \(b\) 和 \(\a\) 的, 以代替 \(a\) 和 \(b\)(也可参见5.2.2节). 由虚拟位点上的力引起的粒子 \(i\), \(j\) 和 \(k\) 上的力为(\(\bi r_\bot\) 的定义如方程4.150):
\(\alg \bi F_i' &= \bi F_s - &{d\cos\q \over |\bi r_{ij}|} \bi F_1 + &{d \sin\q \over |\bi r_\bot|}\left({\bi r_{ij} \cdot \bi r_{jk} \over \bi r_{ij} \cdot \bi r_{ij}} \bi F_2 + \bi F_3\right) \\ \bi F_j' &= &{d\cos\q \over |\bi r_{ij}|} \bi F_1 - &{d \sin\q \over |\bi r_\bot|}\left(\bi F_2+{\bi r_{ij} \cdot \bi r_{jk} \over \bi r_{ij} \cdot \bi r_{ij}} \bi F_2 + \bi F_3\right) \\ \bi F_k' &= &{ } &{d \sin\q \over |\bi r_\bot|}\bi F_2 \\ \bi F_1 &= \bi F_s-{\bi r_{ij} \cdot \bi F_s \over \bi r_{ij} \cdot \bi r_{ij} } \bi r_{ij} \\ \bi F_2 &= \bi F_1-{\bi r_\bot \cdot \bi F_s \over \bi r_\bot \cdot \bi r_\bot } \bi r_\bot \\ \bi F_3 &= \bi {\bi r_{ij} \cdot \bi F_s \over \bi r_{ij} \cdot \bi r_{ij} } \bi r_\bot \tag{4.151} \ealg\)
3out. 三个原子的非线性组合, 平面外(图4.19 3out):
\[\bi r_s = \bi r_i+a\bi r_{ij}+b\bi r_{ik}+c(\bi r_{ij} \times \bi r_{ik}) \tag{4.152}\]
构建的虚拟位点位于其他原子构成的平面外. 由虚拟位点上的力引起的粒子 \(i\), \(j\) 和 \(k\) 上的力为:
\[\alg \bi F_j' &= \bmat a & -cz_{ik} & cy_{ik} \\ cz_{ik} & a & -cx_{ik} \\ -cy_{ik} & cx_{ik} & a \ebmat \bi F_s \\ \bi F_k' &= \bmat b & cz_{ij} & -cy_{ij} \\ -cz_{ij} & b & cx_{ij} \\ cy_{ij} & -cx_{ij} & b \ebmat \bi F_s \\ \bi F_i' &= \bi F_s - \bi F_j' -\bi F_k' \ealg \tag{4.153}\]
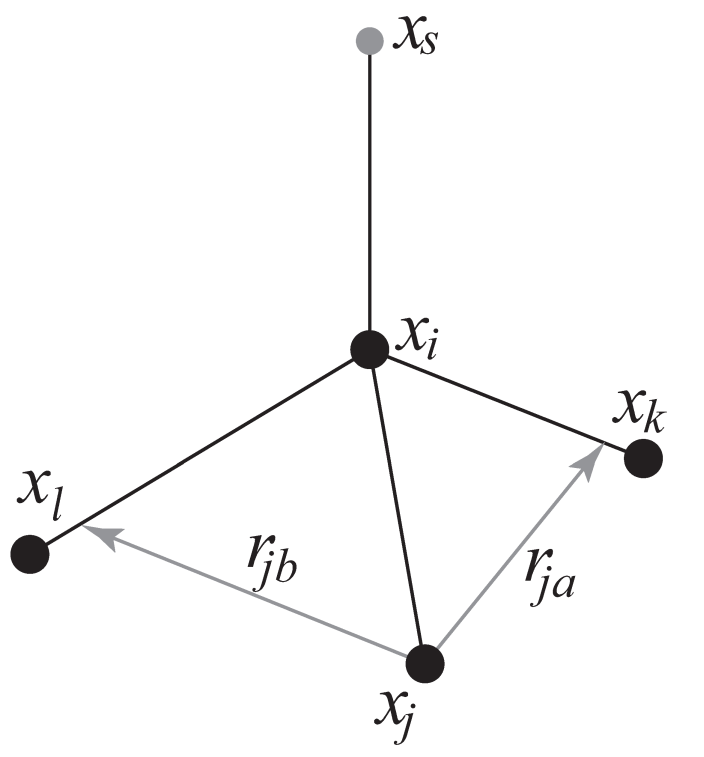
4fdn. 由四个原子构建, 具有固定的距离, 见图4.20. 这种构建有点复杂. 由于之前的构建类型(4fd)不稳定, 这迫使我们引入了这种更加复杂的构建:
\(\alg \bi r_{ja} &= a \bi r_{ik}-\bi r_{ij} = a(\bi x_k-\bi x_i)-(\bi x_j-\bi x_i) \\ \bi r_{jb} &= b \bi r_{il}-\bi r_{ij} = b(\bi x_l-\bi x_i)-(\bi x_j-\bi x_i) \\ \bi r_m &= \bi r_{ja} \times \bi r_{jb} \\ \bi x_s &= \bi x_i+c{\bi r_m \over |\bi r_m|} \tag{4.154} \ealg\)
这种情况下虚拟位点与原子 \(i\) 的距离为 \(|c|\), \(a\) 和 \(b\) 是参数. 注意, 为节省浮点运算的时间, 没有对矢量 \(\bi r_{ik}\) 和 \(\bi r_{ij}\) 进行归一化. 由虚拟位点上的力引起的粒子 \(i\), \(j\) 和 \(k\) 上的力可通过对构造表达式使用链式规则求导计算. 这种构建精确并保持能量守恒, 但确实导致了相对冗长的表达式, 在这里我们没有给出所有表达式(超过200次浮点运算). 感兴趣的读者可以阅读vsite.c中的代码. 幸运的是, 这种虚拟位点类型通常只用于手性中心, 例如蛋白质中的 \(C_\a\) 原子.
新的4fdn构造在拓扑中的’type’识别值为2. GROMACS内部依然支持以前的4fd类型(’type’值为1), 但不应将其用于新的模拟. 所有目前的GROMACS程序都会自动创建4fdn类型作为替代.
N. \(N\) 个原子的线性组合, 相对权重为 \(a_i\). 原子 \(i\) 的权重为:
\[\w_i=a_i\left(\Sum_{j=1}^N a_j \right)^{-1}\tag{4.155}\]
设置权重时有三个选项:
- COG 几何中心: 等权重
- COM 质量中心: \(a_i\) 为原子 \(i\) 的质量. 在自由能模拟中, 原子的质量会改变, 只有A状态的质量会用于权重
- COW 权重中心: \(a_i\) 由用户定义
4.8 长程静电作用
4.8.1 Ewald 加和
\(N\) 个粒子及其周期映象的总静电能由下式给出:
\[V={f \over2}\Sum_{n_x}\Sum_{n_y}\Sum_{n_{z^*} } \Sum_i^N \Sum_j^N {q_i q_j \over \bi r_{ij,\bi n} } \tag{4.156}\]
\((n_x,n_y,nz)=\bi n\) 为盒子的索引矢量, 星号表示当 \((n_x,n_y,nz)=(0,0,0)\) 时, 应忽略 \(i=j\) 项. 距离 \(\bi r_{ij}\) 为电荷之间的真实距离, 而不是最小映象之间的距离. 此加和条件收敛, 但收敛非常缓慢.
首次引入时, Ewald加和被用于计算晶体中周期映象的长程相互作用[103]. 采取的方法是将方程4.156中收敛缓慢的单个加和转换为两个快速收敛的项与一个常数项:
\(\alg V &= V_{\text{dir} }+ V_{\text{rec} }+V_0 \tag{4.157} \\ V_{\text{dir} } &= {f \over2}\Sum_{i,j}^N \Sum_{n_x}\Sum_{n_y}\Sum_{n_{z^*} }q_i q_j {\text{erfc}(\b r_{ij,\bi n}) \over r_{ij,\bi n} } \tag{4.158} \\ V_{\text{rec} } &= {f \over2\p V} \Sum_{i,j}^N q_i q_j \Sum_{m_x}\Sum_{m_y}\Sum_{m_{z^*} } {\exp(-(\p \bi m/\b)^2+2\p i \bi m \cdot (\bi r_i-\bi r_j)) \over \bi m^2 } \tag{4.159} \\ V_0 &= -{f \b \over \sqrt \p} \Sum_i^N q_i^2 \tag{4.160} \ealg\)
其中 \(\b\) 参数用于决定直接空间加和与倒易空间加和之间的相对权重, \(\bi m=(m_x,m_y,m_z)\). 这样, 我们可以对直接空间加和使用较短的截断(数量级为1 nm), 对倒易空间加和也可以使用较短的截断(例如每个方向10个波矢). 不幸的是, 倒易空间加和的计算量以 \(N_2\) 增加(或 \(N^{3/2}\), 如果使用更好一点的算法), 因此用于大的体系是不现实的.
使用Ewald方法
不要使用Emald方法, 除非你绝对确定你需要使用. 几乎对所有的情况, 下面的PME方法表现都更好. 如果你依然坚持使用精度的Ewald加和方法, 在你的.mdp文件中输入以下内容, 如果盒子的边长3 nm左右:
coulombtype = Ewald
rvdw = 0.9
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.6
ewald-rtol = 1e-5
盒子尺寸的比例和fourierspacing参数决定了每个方向使用的波矢 \(m_x,m_y,m_z\) 的最大振幅. 例子中对3 nm的立方盒子每个方向将使用11个波矢(从–5到5). ewald-rtol参数为在截断处静电相互作用的相对强度. 减少此值可以得到更加精确的直接空间加和, 但倒易空间加和的精度会略微降低.
4.8.2 PME
Tom Darden提出的粒子网格Ewald方法[12]可提高倒易空间加和的计算速度. 这种方法不直接对波矢进行加和, 而是使用内插方法将电荷分配到网格上. GROMACS实现的PME方法使用了基数B样条插值[13], 通常被称为平滑PME(SPME). 先使用3D FFT算法对格点进行傅里叶变换, 在k空间中利用对格点的单个加和就可以得到倒易空间的能量项.
格点上的势能可利用逆变换进行计算, 通过使用内插因子就可以得到每个原子上的力.
PME算法的复杂度为 \(N\log(N)\), 对中等或大的体系计算速度远远高于普通的Ewald加和方法. 对非常小的体系, 使用Ewald方法可能更好, 因为可以避免建立格点和进行变换的过程. PME的并行化可参见MPMD PME部分(3.17.5).
使用Verlet截断方案时, PME直接空间的势能被移动了一个常数, 使得在截断处的势能为零. 这种移动很小, 由于体系的电荷接近于零, 总的移动非常小, 这与Lennard-Jones势能的情况不同, 那种情况下所有的移动都会被累加起来. 我们使用了移动, 这样力是势能的精确积分.
使用PME
作为在GROMACS中使用PME加和方法的例子, 在你的.mdp文件中指定如下几行:
coulombtype = PME
rvdw = 0.9
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.12
pme-order = 4
ewald-rtol = 1e-5
在这个例子中, fourierspacing参数决定了FFT格点的最大间距(即, 格点数的最小值), pme-order控制插值的阶数. 使用四阶(立方)内插与指定的间距, 静电能应该能精确到 \(5 \cdot 10^-3\). 由于Lennard-Jones能量的精确度更低一些, 还可以轻微地增加间距.
PME可用于压力缩放, 但当心, 在一些体系中各项异性缩放可能会导致虚假的有序结构.
4.8.3 P3M-AD
在GROMACS中, 也可使用Hockney和Eastwood发展的粒子-粒子粒子-网格方法来处理长程静电相互作用[104]. 动力学计算中, 尽管P3M方法是第一个用于分子模拟的高效长程静电方法, 但在原子模拟中, P3M方法很大程度上已经被平滑PME方法(SPME)所取代. 原始P3M方法计算时有一个缺点: 它需要3次3D-FFT后变换来获得粒子上的力. 但P3M并不需要这样, 可以通过对势能进行数值微分得到所需的力, 像在PME中一样. 这样的方法被称为P3M-AD. P3M-AD和PME唯一的不同在于: PME对晶格Green影响函数进行了优化以尽量减小误差. 然而, 在2012年有研究表明, 可以修改SPME影响函数得到P3M[105]. 这意味着P3M-AD误差最小化的优点在PME中可以同样的计算代价和同样的代码获得, 只需增加几行代码修改影响函数. 然而, 对最佳参数设置, P3M-AD误差最小化的效果小于10%. 对于隔行(也称为交错)的格点, P3M-AD确实展现了很大的精度提升, 但GROMACS(目前)并不支持这种处理.
在GROMACS中使用P3M时, 所用的选项与PME完全相同, 只需要选择不同的静电类型即可.
coulombtype = P3M-AD
4.8.4 优化傅里叶变换和PME计算
建议对计算静电相互作用的参数进行优化, 如PME格点尺寸和截断半径. 在运行长的模拟之前, 这尤其重要.
GROMACS中有一个特殊的工具, g_tune_pme, 可用于自动选择格点的最佳大小和PME节点的数目.
4.9 长程范德华相互作用
4.9.1 色散校正
在这一节中, 我们将推导长程校正, 这是由于对Lennard-Jones或Buckingham相互作用使用截断而引起的. 我们假定截断足够大以至于可以安全地忽略斥力项, 因此只须考虑色散项的校正. 由于色散相互作用的本质(我们截断了一个正比于 -r-6的势能), 能量和压力的校正都是负的. 尽管能量的校正通常很小, 对自由能计算却可能很重要, 因计算时需要考虑两种不同哈密顿量之间的差异. 与此相反, 压力的校正很大, 当需要正确的压力时, 在任何情况下都不能忽略, 尤其是对于NPT模拟. 虽然原则上在力场参数化时可以不经校正就使得压力接近期望的实验值, 但这种方法使得参数依赖于截断, 因此不够理想.
能量
如果我们假定超出截断距离 \(r_c\) 后体系变为均相, 色散相互作用对维里的长程贡献就能够解析得到. 两个粒子之间的色散能可写为
\[V_(r_{ij})= -C_6 r_{ij}^{-6} \tag{4.161}\]
相应的力为:
\[\bi F_{ij} = -6 C_6 r_{ij}^{-8} \bi r_{ij} \tag{4.162}\]
在周期性体系中计算全部的势能并不容易, 所以通常会使用间断的或光滑的截断. 记截断处的势能和力分别为 \(V_c\) 和 \(\bi F_c\), 对含有 \(N\) 个粒子, 粒子密度 \(\r=N/V\) 的体系, 色散能的长程贡献为:
\[V_{lr}={1\over2}N\r \int_0^\infty 4\p r^2 g(r)(V(r)-V_c(r)) \rmd r \tag{4.163}\]
我们将使用移位函数对上式进行积分, 它是GROMACS中VdW相互作用的最一般形式. 从0至 \(r_1\), 移位函数具有恒定的差值 \(S\), 超过截断距离 \(r_c\) 后, 移位函数为零. 积分方程4.163, 并假定在半径为 \(r_1\) 的球体内, 粒子密度等于整体密度, 径向分布函数 \(g(r)\) 在 \(r\) 超过 \(r_1\) 后为1:
\(\alg V_{lr} &= {1\over2} N \left(\r \int_0^{r_1} 4\p r^2 g(r) C_6 S \rmd r +\r \int_{r_1}^{r_c} 4 \p r^2(V(r)-V_c(r))\rmd r + \r \int_{r_c}^\infty 4\p r^2V(r) \rmd r \right) \\ &={1\over2} N\left(\left({4\over3}\p \r r_1^3-1\right)C_6 S +\r \int_{r_1}^{r_c}4 \p r^2(V(r)-V_c(r))\rmd r -{4\over3}\p N\r C_6 r_c^{-3} \right)\tag{4.164} \ealg\)
其中, –1项为自相互作用的校正, 对普通截断, 我们只需要假定超过 \(r_c\) 后 \(g(r)\) 等于1, 这样校正可化简为[106]:
\[V_{lr}=-{2\over3}\p N \r C_6 r_c^{-3} \tag{4.165}\]
举例来说, 如果我们考虑一个只含水分子的模拟盒子, 截断半径为0.9 nm, 密度为1 g cm-3, 上面的校正对每个水分子大约是–0.75 kJ mol-1.
对均相的混合物, 我们需要定义一个 平均色散常数
\[\left < C_6\right >={2\over N(N-1)} \Sum_i^N \Sum_{j \gt i}^N C_6(i,j) \tag{4.166}\]
在GROMACS中, 计算此平均值时不考虑被排除的原子对.
对非均相模拟体系, 如脂质界面系统, 若两部分的 \(\left< C_6\right >\) 比较接近, 能量校正也可以适用
维里和压力
体系的标量维里可通过两粒子 \(i\) 和 \(j\) 之间的色散相互作用计算:
\[\X={1\over2} \bi r_{ij} \cdot \bi F_{ij} = 3 C_6 r_{ij}^{-6} \tag{4.167}\]
相应的压力由下式给出:
\[P={2\over3V}(E_{kin}-\X) \tag{4.168}\]
对维里的长程校正为:
\[\X_{lr}={1\over2}N\r \int_0^\infty 4\p r^2 g(r)(\X-\X_c) \rmd r \tag{4.169}\]
假定超过 \(r_1\) 后 \(g(r)\) 为1, 积分得到维里的长程校正:
\(\alg \X_{lr} &={1\over2}N\r\left(\int_{r_1}^{r_c} 4\p r^2(\X-\X_c) \rmd r + \int_{r_c}^\infty 4\p r^2 3 C_6 r_{ij}^{-6} \rmd r \right) \\ &={1\over2}N\r\left(\int_{r_1}^{r_c} 4\p r^2(\X-\X_c) \rmd r + 4\p C_6 r_c^{-3} \right) \tag{4.170} \ealg\)
对普通截断, 压力的校正值为:
\[P_{lr}=-{4\over3}\p C_6 \r^2r_c^{-3} \tag{4.171}\]
对前面水盒子的例子, 每个分子的维里校正是0.75 kJ mol-1, 对SPC水模型相应的压力校正大约是–280 bar.
对于均相混合物, 我们同样可以使用平均色散常数 \(\left< C6\right >\) (方程4.166):
\[P_{lr}=-{4\over3}\p \left< C_6\right > \r^2 r_c^{-3} \tag{4.172}\]
对于非均相体系, 使用方程4.172时的限制与在能量的情况下相同(参见4.9.1节).
4.9.2 Lennard-Jones PME
为了利用Lennard-Jones势能处理截断以外非均相的体系, 我们可以使用粒子网格Ewald方法, 像上面对静电的讨论一样. 在这种情况下修改的Ewald方程变为:
\(\alg V &= V_{\text{dir} }+ V_{\text{rec} }+V_0 \tag{4.173} \\ V_{\text{dir} } &= {1\over2}\Sum_{i,j}^N \Sum_{n_x}\Sum_{n_y}\Sum_{n_{z^*} } {C_6^{ij} g(\b r_{ij,\bi n}) \over r_{ij,\bi n}^6 } \tag{4.174} \\ V_{\text{rec} } &= {\p^{3\over2} \b^3 \over 2V} \Sum_{m_x}\Sum_{m_y}\Sum_{m_{z^*} } f(\p |\bi m|/\b) \times \Sum_{i,j}^N C_6^{ij} \exp[-2\p i \bi m \cdot (\bi r_i-\bi r_j)] \tag{4.175} \\ V_0 &= -{\b^6 \over 12} \Sum_i^N C_6^{ij} \tag{4.176} \ealg\)
\[\tag{4.1}\]
其中 \(\bi m=(m_x,m_y,m_z)\), 参数 \(\b\) 决定了直接空间和倒易空间的权重, \(C^{ij}_6\) 为粒子 \(i\) 和 \(j\) 的组合色散参数. 星号表示当 \((n_x,n_y,n_z)=(0,0,0)\) 时, 应忽略 \(i=j\) 的项. \(\bi r_{ij,\bi n}\) 为粒子之间的真实距离. 根据Essmann的推导[13], 上面引入的函数 \(f\) 和 \(g\) 的定义为:
\(\alg f(x) &=1/3\left[(1-2x^2) \exp(-x^2) + 2x^3 \sqrt \p \text{erfc}(x) \right] \tag{4.177} \\ g(x) &= \exp(-x^2)(1+x^2+{x^4 \over 2}) \tag{4.178} \ealg\)
只要色散参数可以像静电电荷一样按几何规则进行组合(方程4.6), 上面的方法就适用
\[C_{6,\text{geom} }^{ij} \left(C_6^{ii}C_6^{jj} \right) \tag{4.179}\]
对Lorentz-Berthelot组合规则(方程4.7), 倒易部分的加和必须计算七次, 因为色散参数的拆分如下:
\[C_{6,\text{L-B} }^{ij}=(\s_i+\s_j)^6=\Sum_{n=0}^6 P_n\s_i^n \s_j^{(6-n)} \tag{4.180}\]
\(P_n\) 为Pascal三角系数. 对倒易部分, 这导致了不可忽略计算代价, 需要七个独立的FFT, 因此这成为了以前实现LJ-PME的限制因素. 解决这个问题的一个方法是, 使用几何组合规则计算势能倒易部分的近似的相互作用参数, 得到总的相互作用:
\(\alg V(r < r_c) &= \underbrace{C_6^{\text{dir} } g(\b r)r^{-6} }_{\text{直接空间} } + \underbrace{C_{6,\text{geom} }^{\text{recip} }[1-g(\b r)] r^{-6} }_{倒易空间} \\ &= C_{6,\text{geom} }^{\text{recip} } r^{-6} + \left(C_6^{\text{dir} }-C_{6,\text{geom} }^{\text{recip} } \right) g(\b r) r^{-6} \tag{4.181} \\ V(r > r_c) &= \underbrace{C_{6,\text{geom} }^{\text{recip} }[1-g(\b r)] r^{-6} }_{倒易空间} \tag{4.182} \ealg\)
这样可以很好的定义哈密顿量, 且可以显著提高模拟速度. 这个近似确实引入了一些误差, 但由于差异在于倒易空间中计算的相互作用, 与总的相互作用能相比, 影响非常小. 在双脂层模拟中, 使用1.0 nm的截断, 总色散能的相对误差小于0.5%. 更完整的的讨论可参看[107].
在GROMACS中, 我们现在已经能够正确地计算这项相互作用, 方法是从直接空间相互作用中减去倒易空间中使用的近似势能的贡献:
\[V_{\text{dir} }=C_6^{\text{dir} } r^{-6}-C_6^{\text{recip} }[1-g(\b r)] r^{-6} \tag{4.183}\]
当 \(C_6^{\text{dir} }=C_6^{\text{recip} }\) 时, 这项势能将简化为方程4.174中的表达式, 总的相互作用为:
\(\alg V(r < r_c) &= \underbrace{C_6^{\text{dir} } r^{-6} -C_6^{\text{recip} }[1-g(\b r)] r^{-6} }_{\text{直接空间} } + \underbrace{C_6^{\text{recip} }[1-g(\b r)] r^{-6} }_{倒易空间} \\ &= C_6^{\text{dir} } r^{-6} \tag{4.184} \\ V(r > r_c) &= C_6^{\text{recip} }[1-g(\b r)] r^{-6} \tag{4.185} \ealg\)
当 \(C_6^{\text{dir} } \ne C_6^{\text{recip} }\) 时, 直到截断处都会存在未经修改的LJ力, 误差比模拟时直接空间相互作用未考虑倒易空间中使用的近似而导致的误差小一个数量级. 当采用移位的范德华相互作用时, 常数
\[\left(-C_6^{\text{dir} }+C_6^{\text{recip} }[1-g(\b r_c)] \right)r_c^{-6} \tag{4.1}\]
会加到方程4.184中以确保势能在截断处连续. 注意, 当 \(C_6^{\text{dir} }=C_6^{\text{recip} }\) 时上式退化为预期的 \(-C_6 g(\b r_c)r_c^{-6}\), 如方程4.183类似. 除此之外, 可以利用长程色散校正来校正在倒易空间中使用组合规则导致的近似. 这种校正假定, 对截断LJ势能, 粒子分布是均匀的. 但由于组合规则近似导致的误差非常小, 在大多数情况下, 没有必要进行长程校正. 同样注意, 这样的均相校正并不能校正表面张力, 它是非均相性质.
使用LJ-PME
作为在GROMACS中使用使用粒子网格Ewald加和方法计算Lennard-Jones相互作用的例子, 在你的.mdp文件中指定如下几行:
vdwtype = PME
rvdw = 0.9
vdw-modifier = Potential-Shift
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.12
pme-order = 4
ewald-rtol-lj = 0.001
lj-pme-comb-rule = geometric
如果同时启用LJ-PME和静电PME, 应使用同样的傅里叶格点和插值阶数, 因此fourierspacing和pme-order的设置对二者相同. ewald-rtol-lj控制直接空间和倒易空间之间的划分, 方式与ewald-rtol相同. 除此之外, 倒易空间使用的组合规则由lj-pme-comb-rule决定. 如果当前的力场使用Lorentz-Berthelot组合规则, 设置lj-pme-comb-rule = geometric可获得显著的性能提升, 同时精度会略微降低. 有关此方法的细节可在前面的章节中找到.
注意, 使用完全的长程色散校正意味着, 当与库伦PME联用时, rvdw是一个自由参数, 而不必受限于力场的参数化方案. 这样, 为了提高精度和计算速度, 可以对截断, 间距, 阶数和容差项进行优化.
自然, 使用LJ-PME而不是LJ截断会增加倒易空间部分的计算和通信. 因此, 为了使用单纯PME队列并行模拟的最佳负载均衡, 应该使用更多的队列. 这可能改进mdrun使用的自动负载均衡.
4.10 力场
一个力场由两个明显不同的两部分组成:
- 用于产生势能及其导数, 也即力的方程组(称为s). 这些在前边的章节已有详细的论述.
- 用于方程组的参数. 本手册未给出这些参数, 但可以在GROMACS程序的相关数据文件中找到.
在一组方程之内, 可使用各种不同的参数集. 必须当心, 方程与参数的组合应自洽. 一般来说, 后验地改变一些参数是很危险的, 因为对总力的各种贡献是相互关联的. 这意味着原则上在使用之前, 应该记录每一项改动, 通过与实验数据比较进行验证, 发表在预审的杂志上.
GROMACS 5.0.2包括了一些力场, 网上还有额外的一些力场可供使用. 如果你不清楚应该选择哪个力场, 我们推荐GROMOS–96用于联合原子设置, OPLS-AA/L用于全原子参数. 我们将对可用的选项进行详细描述.
全氢力场
基于GROMOS–87的全氢力场几乎等同于正常的GROMOS–87力场, 因为额外的氢原子没有Lennard-Jones相互作用并且电荷为零. 唯一的区别在于键角项和异常二面角项. 此力场仅仅适用于需要精确的氢原子位置的情况, 例如来自NMR测量的距离限制. 当要使用此力场时, 请阅读前面的段落.
4.10.1 GROMOS–96
GROMACS支持GROMOS–96力场[78], 并包含了43A1, 43A2(发展, 改进了烷烃二面角), 45A3, 53A5和53A6参数集中的所有参数. 此外还包括了所有的标准构建单元, 并可以利用pdb2gmx程序自动创建拓扑.
GROMOS–96力场是GROMOS–87力场的进一步发展, 对GROMOS–87力场的蛋白质和小分子进行了改进. 注意, 53A6中的糖类参数确实对应于2004年发表的参数[108], 与45A4中的不同, GROMACS此次为包含这些参数. 45A4参数集对应于这些参数的后一个版本. 然而, 我们不推荐将GROMOS–96力场用于长的烷烃与脂类分子. GROMOS–96力场与GROMOS–87力场的不同之处在于:
- 力场参数
- 键合相互作用参数并未与原子类型相关联
- 四次键伸缩势(4.2.1)
- 基于键角余弦的键角势(4.2.6)
GROMACS和GROMOS–96的实现有两个不同, 当使用两个程序来模拟同样的体系时, 这可能导致结果有少许的不同:
- GROMOS–96中对溶剂的邻区搜索根据溶剂分子的第一个原子进行. GROMACS没有使用这种方法, 但使用电荷组中心进行搜索产生的差别很小
- GROMOS–96中的维里是基于分子的. GROMACS没有使用这种方法, 而是使用了原子的维里
GROMOS–96力场参数化时对Lennard-Jones使用的截断值为1.4 nm, 因此请确保使用的Lennard-Jones截断(rvdw)至少为1.4. 也可以使用更大的截断, 因为超多1.4 nm后Lennard-Jones势能和力几乎为零.
GROMOS–96文件
GROMACS可以读写GROMOS–96的坐标文件和轨迹文件. 这些文件的扩展名应为.g96, 文件可以是GROMOS–96的初始/最终构型文件, 坐标轨迹文件或二者的结合. 文件是固定格式的, 所有浮点数的输出格式为15.9, 因而文件可能会变得非常大. 按给定的顺序, GROMACS支持以下的数据块:
Header block 文件头数据块:
TITLE (mandatory)标题(必需)Frame blocks 帧数据块:
TIMESTEP (optional)时间步(可选)
POSITION/POSITIONRED (mandatory)位置(必需)
VELOCITY/VELOCITYRED (optional)速度(可选)
BOX (optional)盒子(可选)
参看GROMOS–96手册中对数据块的详细描述[78]. 注意 所有GROMACS程序都可以读取压缩(.Z)或gzip压缩(.gz)的文件.
4.10.2 OPLS/AA
4.10.3 AMBER
GROMACS原生支持以下AMBER力场:
- AMBER94 [109]
- AMBER96 [110]
- AMBER99 [111]
- AMBER99SB [112]
- AMBER99SB-ILDN [113]
- AMBER03 [114]
- AMBERGS [115]
4.10.4 CHARMM
GROMACS支持CHARMM力场, 这些力场可用于蛋白质[116, 117], 脂类[118]和核酸[119, 120]. 其中的蛋白质参数(一定程度上的脂类和核酸参数)进行过彻底的验证, 验证时, 会计算势能并将其与利用CHARMM分子模拟包中的标准参数集计算的势能进行比较, 也会考察蛋白质力场在GROMACS特定技术中的表现, 如虚拟位点(支持较大的时间步长)和最近实现的快速隐式溶剂[73]. 验证的细节及其结果可参看Bjelkmar等人的论文[121]. 核酸及HEME相关参数的转换和测试由Michel Cuendet完成.
当在pdb2gmx中选择CHARMM力场时, 默认的选项是使用CMAP(用于扭转校正映射). 若想排除CMAP, 请使用-nocmap选项. GROMACS中实现的CMAP项的基本形式为骨架扭转角 \(\f\) 和 \(\y\) 的函数. CMAP项在.rtp文件中定义, 对每个支持CMAP的残基, 在结尾处使用[ cmap ]语句定义CMAP. 接着的五个原子名称定义了两个扭转角. 原子1–4定义 \(\f\), 原子2–5定义 \(\y\). 相应的原子类型会被匹配到cmap.itp文件中正确的CMAP类型, 它们包含了校正映射.
GROMACS中使用的CHARMM36力场可在http://mackerell.umaryland.edu/charmm_ff.shtml#gromacs找到.
4.10.5 粗粒化力场
粗粒化是减少体系自由度数的一种系统方法. 为此, 典型的做法是以单个珠子代表整个原子组, 粗粒化的力场用于描述珠子之间的有效相互作用. 根据参数化方法的选择, 这些相互作用的函数形式可以很复杂, 且通常使用表格势能.
粗粒模型被设计用于重现参考体系的某些性质, 可以是全原子模型的性质甚至是实验数据. 依据重现的性质, 可使用不同的方法来得到这样的力场. 以下是各种方法的一个不完全列表:
- 守恒自由能
- 单纯形方法
- MARTINI力场(参看下一节)
- 守恒分布(如径向分布函数), 所谓的基于结构的粗粒化
- (迭代)Boltzmann逆
- 逆Monte Carlo
- 守恒力
- 力匹配
注意, 粗粒势能依赖于状态(例如温度, 密度等), 应该根据体系的特点和模拟条件进行重新参数化. 你可以利用, 例如Versatile Object-oriented Toolkit for Coarse-Graining Applications(VOTCA)[122], 来进行重新参数化. 这个软件包被设计用于协助进行系统的粗粒化, 实现了上面提到的大多数算法, 并且具有经过充分测试的GROMACS界面. 它是开源软件, 更多信息请浏览www.votca.org.
4.10.6 MARTINI
MARTINI力场是一组粗粒化参数, 可用于构建许多体系, 包括蛋白质和膜.
4.10.7 PLUM
PLUM力场[123]无溶剂蛋白-膜模型的一个例子, 其中的膜由基于结构的粗粒化导出[124]. 可以在code.google.com/p/plumx找到GROMACS的实现.
