本手册已过时, 不再更新. 如果需要最新手册, 请加入下方QQ群.
- 6.1 自由能计算的实现
- 6.2 平均力势
- 6.3 非均衡牵引
- 6.4 牵引代码
- 6.5 强制旋转
- 6.6 计算电生理学
- 6.7 使用自由能代码计算PMF
- 6.8 移除最快的自由度
- 6.9 粘度计算
- 6.10 表格相互作用函数
- 6.11 混合量子经典模拟技术
- 6.12 自适应分辨率方案
- 6.13 VMD插件用于轨迹文件输入/输出
- 6.14 交互式分子动力学
6.1 自由能计算的实现
计算自由能时, 必须指定两个条件: 结束状态以及连接结束状态的途径. 指定结束状态的方式有两种, 最直接的方法是在拓扑中指定结束状态. 大多数势能函数形式既支持A状态也支持B状态. 每当指定两种状态时, A状态对应于初始自由能态, 而B状态对应于最终的状态.
在一些情况下, 也可以仅仅通过.mdp文件来定义结束状态, 而无须改变拓扑, 这可以通过使用couple-moltype, couple-lambda0, couple-lambda1, couple-intramol等mdp关键词完成. couple-moltype所选定的任何分子类型会自动获得一个B状态(与一个重新定义的A状态), B状态是根据couple-lambda关键词隐式地构建的, couple-lambda0和couple-lambda1定义了出现于A状态(couple-lambda0)和B状态(couple-lambda1)中的非键参数, 可用选项有’q’, ‘vdw’和’vdw-q’, 它们分别代表了库仑, van der Waals或二者的参数, 这些参数在各自的状态中可以被关闭.
一旦定义了结束状态, 就必须定义结束状态之间的途径, 途径只需要在.mdp文件中定义. 从4.6版本开始, \(\l\) 是一个向量, 它的库仑, van der Waals, 键合, 约束, 质量分量都可以独立地进行调整. 这样我们在同一模拟中就可以线性地关闭库仑项, 然后是使用软核势的van der Waals项. 对于副本交换或扩展系综模拟, 这尤其有用. 因为对这两种模拟, 为改进采样, 在同一模拟中对相互作用从有到无的所有途径进行采样非常重要.
fep-lambdas是 \(\l\) 的默认数组, 其值的范围从0到1. 如果没有指定, 其他所有 \(\l\) 数组都会使用此数组中的值. 以前使用单个 \(\l\) 变量控制途径的做法, 可以通过仅使用fep-lambdas定义途径的方法.
例如, 如果你想首先改变库仑项, 然后是van der Waals项, 同时以与van der Waals项同样的速率改变键合项, 并在整个模拟的前三分之二改变约束项, 那么你可以使用下面的 \(\l\) 向量:
coul-lambdas = 0.0 0.2 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0
vdw-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
bonded-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
restraint-lambdas = 0.0 0.0 0.1 0.2 0.3 0.5 0.7 1.0 1.0 1.0
这等价于下面的设置:
fep-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
coul-lambdas = 0.0 0.2 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0
restraint-lambdas = 0.0 0.0 0.1 0.2 0.3 0.5 0.7 1.0 1.0 1.0
在这种情况下, fep-lambda数组作为默认值被填充到键合与van der Waals相互作用的 \(\l\) 数组中. 通常, 最好时明确列出所有的数组, 以确保进行了正确的赋值.
如果你只想打开从A到B的约束, 那么可以使用下面的设置:
restraint-lambdas = 0.0 0.1 0.2 0.4 0.6 1.0
这样, \(\l\) 向量的其他所有分量都将保持A状态的值.
使用热力学积分计算与向量 \(\l\) 对应的自由能时, TI方程变为矢量方程:
\[\D F=\int \left< \nabla H \right> \centerdot \rmd{\vec \l} \tag{6.1}\]
或对有限差分有:
\[\D F \approx \int \sum \left< \nabla H \right> \centerdot \rmd{\l} \tag{6.2}\]
从https://SimTK.org/home/pymbar下载的外部脚本pymbar可以计算根据GROMACS的dhdl.xvg输出自动计算此积分.
6.2 平均力势
平均力势(PMF, potential of mean force)是对构型系综的平均力进行积分得到的势能. 在GROMACS中, 有几种不同的方法可用于计算平均力. 每一种方法都有其局限性, 如下所述.
- 牵引代码: 用于分子或分子组质心之间.
- 使用简谐键或约束的自由能代码: 单个原子之间.
- 位置约束的自由能代码: 改变相对不动原子组的构型.
- 有限情况的牵引代码: 原子组之间, 它们是较大分子的一部分, 其中的键使用了SHAKE或LINCS约束. 如果牵引组较大, 会使用牵引代码.
下面两节中更详细地讨论牵引和自由能代码.
熵效应
当两个原子或两个组的质心之间的距离被约束或束缚时, 由于两个组的旋转, PMF会含有单纯由熵引起贡献[131]. 对于有两个非相互作用质量的体系, 平均力势为:
\[V_{pmf}(r)=-(n_c-1)k_B T \log(r) \tag{6.3}\]
其中 \(n_c\) 为约束的维数(例如: 对正常的约束 \(n_c=3\), 仅在 \(z\) 方向存在约束时, \(n_c=1\)). 是否需要校正这一贡献取决于你需要的PMF. 当你想要将底物牵引到蛋白质中时, 这个熵对应的项确实对要做的功有贡献. 但当计算溶剂中两个溶质之间的PMF以便用于无溶剂的模拟时, 应该移除熵的贡献. 注意, 此项可能显著; 300 K时, 若距离减半, 贡献为3.5 kJ mol-1.
6.3 非均衡牵引
当连续改变两个组之间的距离时, 会对体系做功, 这意味着体系不再处于平衡状态. 尽管在缓慢牵引的极限情况下, 体系会处于平衡状态, 但对于许多体系, 这种极限情况在可行的计算时间内部无法达到. 然而, 使用Jarzynski关系[132], 从两个距离之间的许多非平衡模拟, 可以得到平衡的自由能变化 \(\D G\)
\[\D G_{AB}=-k_B T\log \left< e^{-\b W_{AB}} \right>_A \tag{6.4}\]
其中 \(W_{AB}\) 为强制体系从状态A沿某路径到达状态B所需的功, 尖括号表示对初始状态A的正则系综进行平均, \(\b=1/k_BT\).
6.4 牵引代码
牵引代码会在一对或多对原子组的质量的中心之间施加力或约束. 每个牵引的反应坐标被称为“坐标”, 它作用于两个牵引组. 一个牵引组可以是一个或多个牵引坐标的一部分. 此外, 坐标还可以作用于单个组或空间中的绝对参考位置. 两个组之间的距离可根据1, 2或3个维度来计算, 或者沿着用户定义的向量进行计算. 参考距离可以是恒定的, 或者可以随时间线性变化. 正常情况下, 所有的原子都根据质量进行加权, 但也可以使用额外的加权因子.
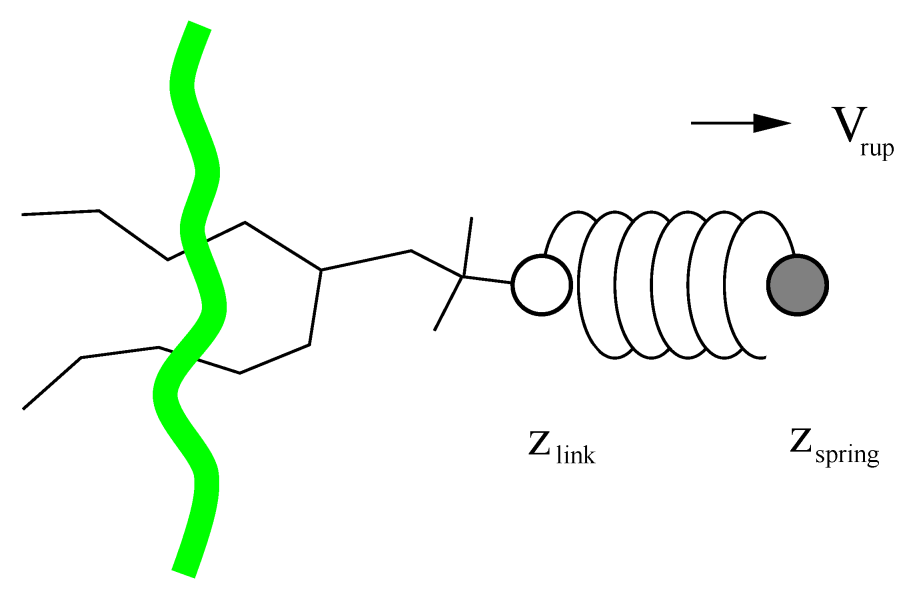
GMX支持三种不同类型的牵引计算, 对所有类型的牵引, 参考距离可以是恒定, 或是随时间线性变化.
- 伞形牵引 在两个组的质心之间施加简谐势. 因此, 力正比于位移.
- 约束牵引 约束两组质心之间的距离. 约束力可以写入到文件中. 此方法使用SHAKE算法, 但当仅约束两个组时, 为精确只需要1次迭代.
- 恒力牵引 在两个质心之间施加恒定的力. 因此, 势能是线性的. 在这种情况下, 牵引速度没有参考距离.
质量中心的定义
在GROMACS中, 有三种方法来定义的一组原子的质量中心. 标准方式是使用“普通”质心, 可能带有附加的权重因子. 使用周期性边界条件时, 就无法再唯一地定义一组原子的质量中心. 因此, 会使用一个参考原子. 为确定质量中心, 对于组中其他所有的原子, 会使用到参考原子最近的周期影象. 这样唯一地定义了质量中心. 默认情况下, 会使用中间的原子(根据拓扑中的顺序)作为参考原子, 但用户也可以选择使用任何其原子, 如果它更接近于组的中心.
对于多层系统, 例如双脂层, 可能需要计算脂分子的PMF, 它是脂分子到整个双层的距离的函数. 在这种情况下, 整个双层可作为参考组, 但也可以为PMF定义更局部的反应坐标. .mdp选项pull_geometry = cylinder并不使用参考组中的所有原子, 而是动态地仅仅使用那些位于圆柱内的原子. 圆柱的半径为r_1, 围绕着通过牵引组的牵引向量. 这仅适用于一维定义的距离, 并且圆柱的长轴沿着定义距离的方向. 也可以使用r_0定义第二个圆柱, 并且使用一个线性切换函数对距离位于r_0和r_1之间的原子进行加权. 这可以平滑原子进出圆柱的的影响(导致牵引力出现跃变).
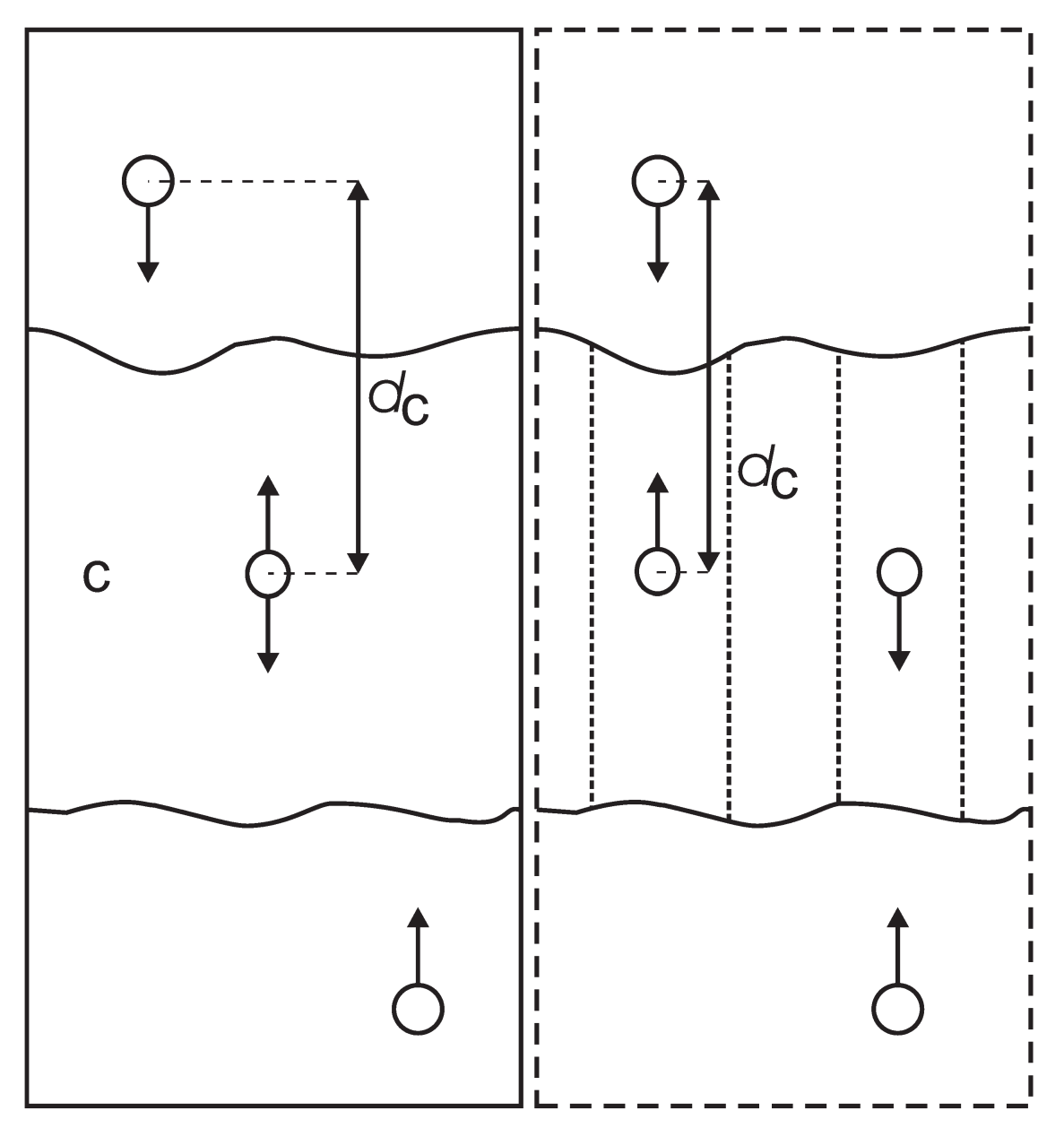
对周期性的体系中的一组分子, 可能无法明确地定义一个普通的参考组. 例如在 \(x\) 和 \(y\) 方向周期性相连, 但在 \(z\) 方向具有两个液-气界面的水板坯. 在这样的设置中, 水分子可以从液体中蒸发, 并穿过蒸汽, 通过周期性边界, 到达另一个界面. 这种体系固有的周期性使得我们无法合适地定义一个沿着 \(z\) 方向的“普通”质心. 一个合适的解决方法对参考组中的所有原子使用一个余弦形的加权剖面. 此剖面单元格胞中的单周期余弦, 并对其相位进行了优化, 使得能够给出权重的最大加和, 包括质量权重. 当所有原子都位于单元格胞长度一半的范围内时, 这种方法提供了唯一和连续的参考位置, 几乎等同于普通的质心位置. 请参看文献[133]了解详细信息.
当在计算过程中使用相对权重 \(\w_i\) 时, 无论是输入中提供的权重, 还是因圆柱几何或余弦加权引入的权重, 都需要对权重进行缩放, 以保证动量守恒:
\[\w_i'= \left. \w_i \Sum_{j=1}^N \w_j m_j \middle/ \Sum_{j=1}^N \w_j^2 m_j \right. \tag{6.5}\]
其中 \(m_i\) 为组中原子 \(j\) 的质量. 计算约束力时所需要的组的质量为:
\[M=\sum_{i=1}^N \w_i' m_i \tag{6.6}\]
加权的质量中心的定义为:
\[\bi r_{com}=\left. \sum_{i=1}^N \w_i' m_i \bi r_i \middle/ M \right. \tag{6.7}\]
根据质心, 可计算作用在每组上的AFM, 约束或伞形力 \(\bi F_{com}\). 作用于组质心上的力会按下式重新分配到原子上:
\[\bi F_i = {\w_i' m_i \over M} \bi F_{com} \tag{6.8}\]
局限性
有一个理论局限性: 严格的来说, 只能计算某些组之间的约束力, 这些组没有通过约束连接到体系的其余部分. 如果一个组包含的一部分分子的键长被约束, 应该同时迭代牵引约束和LINCS或SHAKE的键约束算法. GROMACS还无发做到这点. 这意味着, 若模拟时在.mdp文件中使用了constraints = all-bonds选项, 严格地说, 牵引仅限于整个分子或分子组. 在一些情况下, 通过使用自由能代码可以避免此限制,参加6.7节. 在实践中, 当牵引组包含大量原子和/或牵引力很小时, 因不对两种约束算法同时进行迭代导致的误差可忽略不计. 在这些情况下, 相比于键长, 牵引组的约束校正唯一很小.
6.5 强制旋转
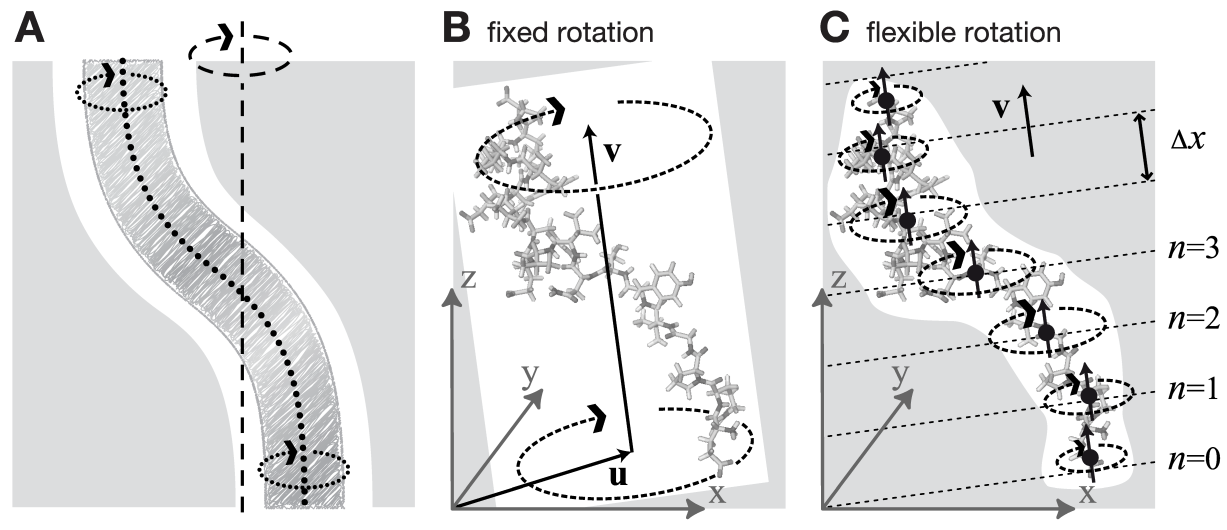
这个模块可用于强制一组原子进行旋转, 例如一个蛋白质亚基的旋转. 有多种旋转势能, 其中复杂的类型, 在模拟过程中允许灵活地适应旋转亚基以及局部旋转轴. 一个示例应用可以在文献[134]中找到.
6.5.1 固定轴旋转
具有各向同性势的固定轴
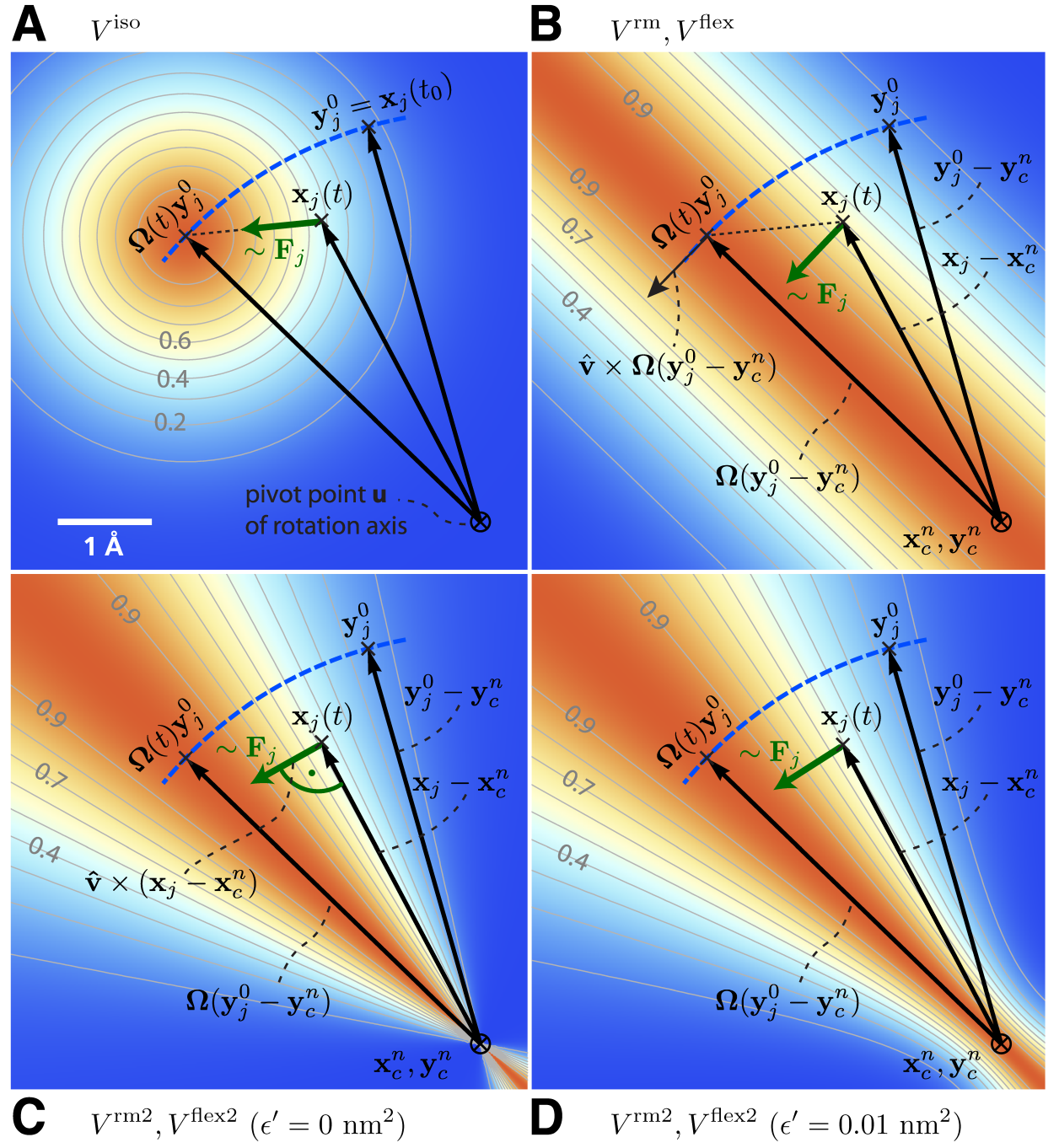
在固定轴方法中(参见图6.3 B), 对一组 \(N\) 个, 位置为 \(\bi x_i\) 的原子(记为“旋转组”), 作用于其上的力矩是通过旋转一组参考原子位置-通常是他们的初始位置 \(\bi y_i^0\)-施加的, 旋转以恒定角速度 \(\w\) 绕着由方向向量 \(\hat{\bi v}\) 和支点 \(\bi u\) 定义的轴线进行. 为此, 每个位置为 \(\bi x_i\) 的原子利用“虚拟”弹簧势能附着到它移动的参考位置 \(\bi y_i=\bi \W(t)(\bi y^0_i- \bi u)\), 其中 \(\bi \W(t)\) 是一个矩阵, 描述了绕轴的旋转. 对最简单的情况, “弹簧”是利用简谐势描述的,
\[V^{\text{iso} }= {k\over2} \Sum_{i=1}^N \w_i \left[ \bi \W(t)(\bi y_i^0-\bi u)-(\bi x_i-\bi u) \right]^2 \tag{6.9}\]
并具有可选的质量加权前因子 \(\w_i = N m_i/M\), 总质量 \(M=\S_{i=1}^N m_i\). 旋转矩阵 \(\bi \W(t)\) 为
\[\bi \W(t)=\pmat \cos \w t + v_x^2\x & v_x v_y\x - v_z \sin \w t & v_x v_z\x + v_y \sin \w t \\ v_x v_y\x + v_z \sin \w t & \cos \w t + v_y^2\x & v_y v_z\x - v_x \sin \w t \\ v_x v_z\x - v_y \sin \w t & v_y v_z\x + v_x \sin \w t & \cos \w t+v_z^2\x \\ \epmat\]
其中 \(v_x, v_y, v_z\) 为归一化的旋转向量 \(\hat v\) 的分量, \(\x:= 1-\cos(\w t)\). 如图6.4A所示, 对单个原子 \(j\), 旋转矩阵 \(\bi \W(t)\) 作用于 \(t=t_0\) 时刻原子 \(j\) 的初始参考位置 \(\bi y_j^0=\bi x_j(t_0)\). 在其后的时刻 \(t\), 参考位置已旋转远离其初始位置(沿蓝色虚线), 从而产生力
\[\bi F_j^{\text{iso}}=-\nabla_j V^{\text{iso}}=k \w_j \left[\bi \W(t) (\bi y_j^0- \bi u)-(\bi x_j-\bi u)\right] \tag{6.10}\]
此力指向参考位置.
无支点各向同性势
不使用固定的支点矢量 \(\bi u\), 该势能使用旋转组的质量中心 \(\bi x_c\) 作为旋转轴的支点,
\[\bi x_c={1 \over M}\sum_{i=1}^N m_i \bi x_i, \;\; \bi y_c^0={1 \over M}\sum_{i=1}^N m_i \bi y_i^0 \tag{6.11}\]
这就得到了了“无支点”的各向同性势
\[V^{\text{iso-pf}}={k\over2} \Sum_{i=1}^N \w_i \left[\bi \W(t)(\bi y_i^0-\bi y_c^0)-(\bi x_i-\bi x_c)\right]^2 \tag{6.12}\]
相应的力为
\[F^{\text{iso-pf}}= k\w_j \left[\bi \W(t)(\bi y_j^0-\bi y_c^0)-(\bi x_j-\bi x_c)\right] \tag{6.13}\]
如果不使用质量加权, 支点 \(\bi x_c\) 为组的几何中心.
平行运动势的变体
由各向同性势产生的力(方程6.9和6.12)还含有平行于旋转轴的成分, 从而限制了沿整个旋转组(对 \(V^{\text{iso} }\))轴线或旋转组内(对 \(V^{\text{iso-pf} }\))轴线的运动. 如果倾向于不限制沿轴线的运动, 我们已经通过消除势能所有平行于旋转轴的分量实现了“平行运动”的一种变体. 通过投影参考和实际位置之间的距离向量
\[\bi r_i=\bi \W(t)(\bi y_i^0-\bi u)-(\bi x_i-\bi u) \tag{6.14}\]
到垂直于旋转矢量的平面上,
\[\bi r_i^{\bot} := \bi r_i-(\bi r_i \cdot \hat{\bi v}) \hat{\bi v} \tag{6.15}\]
得到
\(\alg V^{\text{pm} } &= {k \over 2} \Sum_{i=1}^N \w_i(\bi r_i^\bot)^2 \\ &= {k\over2}\Sum_{i=1}^N \w_i \{ \bi \W(t)(\bi y_i^0-\bi u)-(\bi x_i-\bi u) \\ &-\left\{\left[\bi \W(t)(\bi y_i^0-\bi u)-(\bi x_i-\bi u)\right] \cdot \hat{\bi v} \right\} \hat{\bi v} \}^2 \tag{6.16} \ealg\)
同样的
\[\bi F_j^{\text{pm}}=k\w_j \bi r_j^{\bot} \tag{6.17}\]
无支点的平行运动势
将方程6.16中的固定支点 \(\bi u\) 替换为质量中心 \(\bi x_c\) 就得到了平行运动势无支点的变体形式. 对
\[\bi s_i=\bi \W(t)(\bi y_i^0-\bi y_c^0)-(\bi x_i-\bi x_c) \tag{6.18}\]
各自的势能和力为
\(\alg V^{\text{pm-pf}} &={k\over2}\sum_{i=1}^N \w_i(\bi s_i^{\bot})^2 \tag{6.19} \\ \bi F_j^{\text{pm-pf}} &=k\w_j \bi s_j^{\bot} \tag{6.20} \ealg\)
径向运动势
在上述变体中, 转动势能的最小点位于参考位置 \(\bi y_i\) 上的一个点(对各向同性势), 或者是通过 \(\bi y_i\) 平行于旋转轴的一条线(对平行运动势). 结果, 径向力限制了原子的径向运动. 接下来的两类旋转势, \(V^{\text{rm} }\) 和 \(V^{\text{rm2} }\), 大大减少甚至消除了这种效应. 第一类变体势, \(V^{\text{rm} }\)(图6.4B), 消除了所有平行于连接参考原子和旋转轴向量的力的分量,
\[V^{\text{rm}}={k\over2}\sum_{i=1}^N \w_i[ \bi p_i \cdot (\bi x_i-\bi u)]^2 \tag{6.21}\]
其中
\[\bi p_i:={ \hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi u) \over \| \hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi u) \|} \tag{6.22}\]
该变体只取决于原子 \(i\) 到由 \(\hat{\bi v}\) 和 \(\bi \W(t)(\bi y_i^0-\bi u)\) 张成的平面的距离 \(\bi p_i \cdot(\bi x_i - \bi u)\). 相应的力为
\[\bi F_j^{\text{rm}}=-k\w_j \left[ \bi p_j \cdot (\bi x_j-\bi u)\right] \bi p_j \tag{6.23}\]
无支点的径向运动势
类似于无支点的各向同性势, 我们可以得到上面势能无支点的形式. 对
\[\bi q_i:={ \hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi u) \over \| \hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi u) \|} \tag{6.24}\]
对这种径向运动势无支点的变体形式, 势能和力分别为
\(\alg V^{\text{rm-pf}} &={k\over2}\sum_{i=1}^N \w_i [\bi q_i \cdot (\bi x_i-\bi x_c)]^2 \tag{6.25} \\ \bi F_j^{\text{rm-pf}} &= -k \w_j \left[ \bi q_j \cdot (\bi x_j-\bi x_c)\right] \bi q_j +k{m_j\over M}\Sum_{i=1}^N \w_i[\bi q_i \cdot (\bi x_i -\bi x_c)] \bi q_i \tag{6.26} \ealg\)
二型径向运动势
如图6.4B, 由 \(V^{\text{rm} }\) 产生的力仍包含小的二阶径向分量. 大多数情况下, 这种扰动可以容忍; 如果不能容忍, 可以使用备选的势能函数 \(V^{\text{rm2} }\), 它完全消除了力径向部分的贡献, 如图6.4C所示,
\[V^{\text{rm2}} ={k\over2} \Sum_{i=1}^N \w_i { [ (\hat{\bi v} \times (\bi x_i-\bi u) \cdot \bi \W(t)(\bi y_i^0-\bi u)]^2 \over \| \hat{\bi v} \times (\bi x_i-\bi u) \|^2 +\e'} \tag{6.27}\]
其中, 引入了小参数 \(\e'\) 以避免奇异性. 对 \(\e'=0\) nm2, 等势能平面由 \(\bi x_i-\bi u\) 和 \(\hat{\bi v}\) 张成, 得到的力垂直于 \(\bi x_i-\bi u\), 因此不会再压缩会扩展远离或朝向旋转轴的结构部分.
在方程6.27的分母中使用一个小的正值的 \(e'\)(例如, \(\e'= 0.01\) nm2, 图6.4D)会得到一个定义良好的势能函数, 并且连续的力也靠近旋转轴, 但 \(\e'=0\) nm2时(图6.4C)不是这样. 对
\(\alg \bi r_i &:=\bi \W(t)(\bi y_i^0-\bi u) \tag{6.28} \\ \bi s_i &:={\hat{\bi v} \times (\bi x_i-\bi u) \over \|\hat{\bi v} \times (\bi x_i-\bi u)\|} \equiv \Y_i \hat{\bi v} \times (\bi x_i-\bi u) \tag{6.29} \\ \Y_i^* &:= {1 \over \|\hat{\bi v} \times (\bi x_i-\bi u)\|^2+\e'} \tag{6.30} \ealg\)
作用在原子 \(j\) 上的力为
\[\bi F_j^{\text{rm2} }=-k \left\{ \w_j(\bi s_j \cdot \bi r_j) \left[ {\Y_j^* \over \Y_j} \bi r_j-{\Y_j^{*2} \over \Y_j^3} (\bi s_j \cdot \bi r_j) \bi s_j \right] \right\} \times \hat{\bi v} \tag{6.31}\]
二型无支点径向运动势
上面势能的无支点变体形式为
\[V^{\text{rm2-pf} }={k \over 2} \Sum_{i=1}^N \w_i { [(\hat{\bi v} \times (\bi x_i-\bi x_c)) \cdot \bi \W(t)(\bi y_i^0-\bi y_c)]^2 \over \|\hat{\bi v} \times (\bi x_i-\bi x_c) \|^2+ \e'} \tag{6.32}\]
其中
\(\alg \bi r_i &:= \W(t)(\bi y_i^0-\bi y_c) \tag{6.33} \\ \bi s_i &:= {\hat{\bi v} \times (\bi x_i-\bi x_c) \over \|\hat{\bi v} \times (\bi x_i-\bi x_c)\|} \equiv \Y_i \hat{\bi v} \times (\bi x_i-\bi x_c) \tag{6.34} \\ \Y_i^* &:={1\over \|\hat{\bi v} \times (\bi x_i-\bi x_c) \|^2+\e'} \tag{6.35} \ealg\)
作用于原子 \(j\) 上的力为
\(\alg \bi F_j^{\text{rm2-pf} } = &-k\left\{ \w_j (\bi s_j \cdot \bi r_j) \left[ {\Y_j^* \over \Y_j} \bi r_j-{\Y_j^{*2} \over \Y_j^3} (\bi s_j \cdot \bi r_j) \bi s_j\right]\right\} \times \hat{\bi v} \\ &+k{m_j \over M} \left\{ \Sum_{i=1}^N \w_i (\bi s_i \cdot \bi r_i) \left[ {\Y_i^* \over \Y_i} \bi r_i-{\Y_i^{*2} \over \Y_i^3} (\bi s_i \cdot \bi r_i) \bi s_i\right]\right\} \times \hat{\bi v} \tag{6.36} \ealg\)
6.5.2 柔性轴旋转
如图6.3A-B所示, 固定轴旋转方案的刚体行为对于许多应用而言是一个缺点. 特别是, 当平衡的原子位置直接依赖于参考位置时, 旋转组的变形会被抑制. 为避免这种限制, 现在将方程6.26和6.32推广到图6.3C示意的“柔性轴”. 具体做法是将旋转组划分为一些列等间距的板坯, 每个板坯垂直于旋转向量, 并对每个板坯施加独立的旋转势. 图6.3C中点线表示板坯的中间平面, 大的黑点表示板坯的中心.
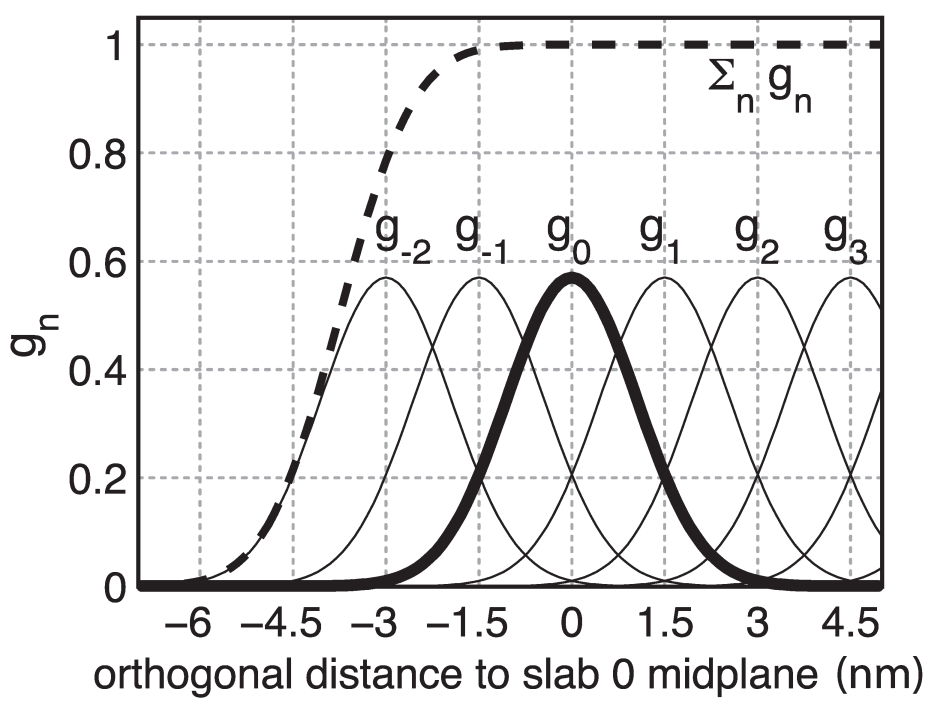
为避免势能与力的不连续性, 我们定义了“软板坯”, 根据每个板坯 \(n\) 对总势能函数 \(V^{\text{flex} }\) 的贡献进行加权, 加权时使用高斯函数
\[g_n(\bi x_i)=\G \exp\left(-{\b_n^2(\bi x_i) \over 2\s^2}\right) \tag{6.37}\]
其中心位于第 \(n\) 个板坯中间的平面上. 这里的 \(\s\) 为高斯函数的宽度, \(\D x\) 为相邻板坯间的距离,
\[\b_n(\bi x_i) := \bi x_i \cdot \hat{\bi v} - n \D x \tag{6.38}\]
最方便的一个选择是 \(\s=0.7 \D x\), 并且
\[1/\G=\Sum_{n \in Z} \exp \left(-{(n-{1\over4})^2 \over 2 \cdot 0.7^2} \right) \approx 1.75464\]
这样得到的总和几乎是恒定的, 基本上与 \(\bi x_i\) 无关(图6.5中虚线所示), 即
\[\Sum_{n\in Z} g_n(\bi x_i)=1+\e(\bi x_i) \tag{6.39}\]
其中 \(\abs{\e(\bi x_i)} <1.3 \cdot 10^{-4}\). 这一选择也意味着板坯对力的各自贡献加起来等于1, 这样就不再需要进一步的归一化了.
对每个板坯中心 \(\bi x_c\), 所有原子的贡献来源于其高斯加权的(也可选择使用质量加权)位置向量 \(g_n(\bi x_i) \bi x_i\). 瞬时板坯中心 \(\bi x_c^n\) 根据当前位置 \(\bi x_i\) 进行计算
\[\bi x_c^n={\S_{i=1}^N g_n(\bi x_i) m_i \bi x_i \over \S_{i=1}^N g_n(\bi x_i) m_i} \tag{6.40}\]
而参考中心 \(\bi y_c^n\) 根据参考位置 \(\bi y_i^0\) 进行计算
\[\bi y_c^n ={\S_{i=1}^N g_n(\bi y_i^0) m_i \bi y_i^0 \over \S_{i=1}^N g_n(\bi y_i^0) m_i} \tag{6.41}\]
由于 \(g_n\) 衰减很快, 每个板坯将主要涉及距板坯中心 \(\approx 3\D x\) 内的原子的贡献.
柔性轴势
我们考虑两种柔性轴的变体. 在第一种变体中, 将高斯加权的板坯划分过程应用到径向运动势中(方程6.26/图6.4B)中, 就得到了板坯 \(n\) 的贡献
\[V^n={k\over2} \Sum_{i=1}^N \w_i g_n(\bi x_i)[ \bi q_i^n \cdot (\bi x_i-\bi x_c^n)]^2\]
总的势能函数
\[V^{\text{flex} }=\Sum_n V^n \tag{6.42}\]
注意, 方程6.26中使用的全局质心 \(\bi x_c\) 现在被 \(\bi x_c^n\) 代替, 它是板坯的质心. 对
\(\alg \bi q_i^n &:={\hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi y_c^n) \over \| \hat{\bi v} \times \bi \W(t)(\bi y_i^0-\bi y_c^n)\|} \tag{6.43} \\ b_i^n &:= \bi q_i^n \cdot (\bi x_i-\bi x_c^n) \tag{6.44} \ealg\)
作用在原子 \(j\) 上的力为
\(\alg \bi F_j^{\text{flex} }= &-k \w_j \Sum_n g_n(\bi x_j) b_j^n \left\{\bi q_j^n-b_j^n {\b_n(\bi x_j) \over 2\s^2} \hat{\bi v} \right\} \\ &+k m_j \Sum_n {g_n(\bi x_j) \over \S_h g_n(\bi x_h)} \Sum_{i=1}^N \w_i g_n(\bi x_i) b_i^n \left\{ \bi q_i^n- {\b_n(\bi x_j) \over \s^2} [\bi q_i^n \cdot (\bi x_j-\bi x_c^n)] \hat{\bi v} \right\} \tag{6.45} \ealg\)
注意, 对定义的 \(V^{\text{flex} }\), 板坯在空间中是固定的, 参考中心 \(\bi y_c^n\) 也一样. 如果在模拟中, 旋转组沿 \(\bi v\) 方向移动得太远, 它可能会进入一个没有定义参考板坯中心的区域-由于缺少附近的参考位置-这样就不可能对势能进行计算. 因此, 对这个势能, 我们给出了一个略加修改的版本, 它能够避免前面所说的问题, 具体做法是将板坯 \(n=0\) 的中间平面附着到旋转组的中心, 这样得到的板坯会与旋转组一起移动. 通过从位置中减去组的质心 \(\bi x_c\),
\[\tilde{\bi x}_i=\bi x_i-\bi x_c, \tilde{\bi y}_i^0=\bi y_i^0-\bi y_c^0 \tag{6.46}\]
这样
\[V^{\text{flex2} }={k\over2} \Sum_n \Sum_{i=1}^N \w_i g_n(\tilde{\bi x_i}) \left[ { (\hat{\bi v} \times \bi \W(t)(\tilde{\bi y}_i^0-\tilde{\bi y}_c^n) \over \|\hat{\bi v} \times \bi \W(t)(\tilde{\bi y}_i^0-\tilde{\bi y}_c^n)\|} \cdot (\tilde{\bi x}_i-\tilde{\bi x}_c^n) \right]^2 \tag{6.47}\]
为了简化力的导数, 以及出于效率的考虑, 我们在这里假定 \(\bi x_c\) 是恒定的, 因此 \(\partial \bi x_c/\partial x = \partial \bi x_c/\partial y=\partial \bi x_c/\partial z=0\), 这种得到的力误差很小(数量级为 \(O(1/N)\) 或 \(O(m_j/M)\), 如果使用质量加权的话), 因此可以容忍. 利用这一假定, 力 \(\bi F^{\text{flex-t} }\) 与方程6.45具有相同的形式.
二型柔性轴势
第二种变体是将势 \(V^{\text{rm2} }\)(方程6.32)用于划分的板坯, 得到了无径向力贡献的柔性轴(图6.4C)
\[V^{\text{flex2} }={k\over2} \Sum_{i=1}^N \Sum_n \w_i g_n(\bi x_i) { [(\hat{\bi v} \times (\bi x_i-\bi x_c^n)) \cdot \bi \W(t) (\bi y_i^0-\bi y_c^n)]^2 \over \| \hat{\bi v} \times (\bi x_i-\bi x_c^n) \|^2+\e'} \tag{6.48}\]
其中
\(\alg \bi r_i^n &:= \bi \W(t)(\bi y_i^0-\bi y_c^n) \tag{6.49} \\ \bi s_i^n &:= {\hat{\bi v} \times (\bi x_i-\bi x_c^n) \over \| \hat{\bi v} \times (\bi x_i-\bi x_c^n) \|} \equiv \y_i \hat{\bi v} \times (\bi x_i-\bi x_c^n) \tag{6.50} \\ \y_i^* &:={1 \over \| \hat{\bi v} \times (\bi x_i-\bi x_c^n)\|^2+\e'} \tag{6.51} \\ W_j^n &:= {g_n(\bi x_j) m_j \over \s_h g_n(\bi x_h) m_h } \tag{6.52} \\ \bi S^n &:= \Sum_{i=1}^N \w_i g_n(\bi x_i)(\bi s_i^n \cdot \bi r_j^n) \left[ {\y_i^* \over \y_i} \bi r_i^n-{\y_i^{*2} \over \y_i^3}(\bi s_i^n \cdot \bi r_i^n) \bi s_i^n \right] \tag{6.53} \ealg\)
作用于原子 \(j\) 上的力为
\(\alg \bi F_j^{\text{flex2} } = & -k\left\{ \Sum_n \w_j g_n(\bi x_j) (\bi s_j^n \cdot \bi r_j^n) \left[ {\y_j^* \over \y_j} \bi r_j^n-{\y_j^{*2} \over \y_j^3} (\bi s_j^n \cdot \bi r_j^n) \bi s_j^n\right] \right\} \times \hat{\bi v} \\ & +k\left\{ \Sum_n W_j^n \bi S^n \right\} \times \hat{\bi v} -k \left\{ \Sum_n W_j^n {\b_n(\bi x_j) \over \s^2} {1\over \y_j} \bi s_j^n \cdot \bi S^n \right\} \hat{\bi v} \\ & +{k \over 2}\left\{ \Sum_n \w_j g_n(\bi x_j) {\b_n(\bi x_j) \over \s^2} {\y_j^* \over \y_j^2} (\bi s_j^n \cdot \bi r_j^n)^2 \right\} \hat{\bi v} \tag{6.54} \ealg\)
应用变换(6.46)可得到二型柔性势“耐平动”的形式, \(V^{\text{flex2-t} }\). 再次, 假定 \(\partial \bi x_c/\partial x\), \(\partial \bi x_c/\partial y\), \(\partial \bi x_c/\partial z\) 很小, 得到的方程 \(V^{\text{flex2-t} }\) 和 \(\bi F^{\text{flex2-t} }\) 分别类似于 \(V^{\text{flex2} }\) 和 \(\bi F^{\text{flex2} }\).
6.5.3 用法
为使用应用强制旋转, 可通过.mdp输入文件中的rot_group0, rot_group1等索引组定义受到旋转势能作用的粒子 \(i\). 参考位置 \(\bi y_i^0\) 由提供给grompp的特殊.trr文件中读取. 如果发现发现这样的文件, 会使用 \(\bi x_i(t=0)\) 作为参考位置, 并写入.trr, 这样它们就可以用于随后的设置. 势能的所有参数, 如 \(k\), \(\e'\) 等(表 6.1 ). 由.mdp参数提供; rot_type选择势能的类型. 选项rot_massw选择是否使用质量加权平均. 对柔性势能, 截断值 \(g_n^{\text{min} }\)(典型值为0.001), 可确保只计算对 \(V\) 和 \(F\) 有显著贡献的部分, 即那些 \(g_n(\bi x) < g_n^{\text{min} }\) 的项被省略. 表6.2总结了写入到附加输出文件的一些量, 将在下面讨论它们.
| 参数 | \(k\) | \(\hat{\bi v}\) | \(\bi u\) | \(\w\) | \(\e'\) | \(\D x\) | \(g_n^{\text{min}}\) | ||
.mdp输入变量名 |
k | vec | pivot | rate | eps | slab_dist | min_gauss | ||
| 单位 | kJ mol nm-2 | - | nm | o/ps | nm2 | nm | - | ||
| 固定轴势能: | 方程 | ||||||||
| 各向同性 \(V^{\text{iso} }\) | (6.9) | X | X | X | X | - | - | - | |
| -无支点 \(V^{\text{iso-pf} }\) | (6.12) | X | X | - | X | - | - | - | |
| 平行运动 \(V^{\text{pm} }\) | (6.16) | X | X | X | X | - | - | - | |
| -无支点 \(V^{\text{pm-pf} }\) | (6.20) | X | X | - | X | - | - | - | |
| 径向运动 \(V^{\text{rm} }\) | (6.21) | X | X | X | X | - | - | - | |
| -无支点 \(V^{\text{rm-pf} }\) | (6.26) | X | X | - | X | - | - | - | |
| 二型径向 \(V^{\text{rm2} }\) | (6.27) | X | X | X | X | X | - | - | |
| -无支点 \(V^{\text{rm2-pf} }\) | (6.32) | X | X | - | X | X | - | - | |
| 柔性轴势能: | 方程 | ||||||||
| 柔性 \(V^{\text{flex} }\) | (6.42) | X | X | - | X | - | X | X | |
| -耐平动 \(V^{\text{flex-t} }\) | (6.47) | X | X | - | X | - | X | X | |
| 二型柔性势 \(V^{\text{flex2} }\) | (6.48) | X | X | - | X | X | X | X | |
| -耐平动 \(V^{\text{flex2-t} }\) | - | X | X | - | X | X | X | X | |
| 物理量 | 单位 | 方程 | 输出文件 | 固定 | 可变 | |
|---|---|---|---|---|---|---|
| \(V(t)\) | kJ/mol | 参见6.1 | rotation |
X | X | |
| \(\q_{\text{ref} }(t)\) | 度 | \(\q_{\text{ref} }(t)=\w t\) | rotation |
X | X | |
| \(\q_{\text{av} }(t)\) | 度 | (6.55) | rotation |
X | - | |
| \(\q_{\text{fit} }(t),\q_{\text{fit} }(t,n)\) | 度 | (6.57) | rotangles |
- | X | |
| \(\bi y_0(n),\bi x_0(t,n)\) | nm | (6.40, 6.41) | rotslabs |
- | X | |
| \(\t(t)\) | kJ/mol | (6.58) | rotation |
X | - | |
| \(\t(t, n)\) | kJ/mol | (6.58) | rottorque |
- | X | |
旋转组的角度: 固定轴
对固定轴旋转, 组相对于参考组的平均角度 \(\q_{\text{av} }(t)\), 是通过所有旋转组原子到其参考位置的距离加权的角度偏差来确定的,
\[\q_{\text{av} }=\Sum_{i=1}^N r_i \q_i/\Sum_{i=1}^N r_i \tag{6.55}\]
这里 \(r_i\) 为参考位置到旋转轴的距离, 偏差角 \(\q_i\) 由原子位置决定, 投射到垂直于旋转轴并通过支点 \(\bi u\) 的平面(参考方程6.15中 \(\bot\) 的定义),
\[\cos\q_i={ (\bi y_i-\bi u)^\bot \cdot (\bi x_i-\bi u)^\bot \over \|(\bi y_i-\bi u)^\bot \cdot (\bi x_i-\bi u)^\bot \|} \tag{6.56}\]
如果实际结构的旋转在参考前, \(\q_{\text{av} }\) 的符号选择使得 \(\q_{\text{av} } >0\).
旋转组角度: 柔性轴
对于柔性轴旋转, 会提供两个输出, 整个旋转组的角度和板坯中片段的分开角度. 确定整个旋转组的角度时, 会使用RMSD匹配将 \(\bi x_i\) 匹配到 \(t=0\) 时刻的参考位置 \(\bi y_i^0\), 得到的 \(\q_{\text{fit} }\) 是参考为达到最佳匹配必须绕 \(\hat v\) 旋转的角度,
\[\text{RMSD}(\bi x_i, \bi \W(\q_{\text{fit} }) \bi y_i^0)\overset{!}{=} \text{min} \tag{6.57}\]
为了确定每个板坯 \(n\) 的局部角度, 会使用板坯 \(n\) 的高斯函数对参考和实际位置进行加权, 方程6.57计算的 \(\q_{\text{fit} }(t,n)\) 来自于高斯加权的位置.
对于所有的角度, .mdp输入选项rot_fit_method控制是进行正常的RMSD匹配, 还是在匹配时将每个位置 \(\bi x_i\) 置于距旋转轴相同的距离作为其参考对应 \(\bi y^0_i\). 对后一种情况, RMSD只测量了角度差异, 不包含径向部分.
通过搜索最小能量确定角度
作为替代方法, 对rot_fit_method = potential, 旋转组的角度取为旋转势能最小时对应的角度. 因此, 需要对围绕当前参考角度的一系列角度计算其对应的旋转势能. 在这种情况下, rotangles.log输出文件包含了所选角度对应的旋转势能值, rotation.xvg列出了最小势能对应的角度.
力矩
对固定轴转动, 旋转势对应的力矩 \(\bi \t(t)\) 如下
\[\bi \t(t)=\Sum_{i=1}^{N} \bi r_i(t) \times \bi f_i^\bot(t) \tag{6.58}\]
其中 \(\bi r_i(t)\) 为旋转轴到 \(\bi x_i(t)\) 的距离向量, \(\bi f_i^\bot(t)\) 为垂直于 \(\bi r_i(t)\) 和 \(\hat{\bi v}\) 的力分量. 对柔性轴旋转, 会使用板坯的局部旋转轴和高斯加权的位置计算每个板坯的 \(\bi \t_n\).
6.6 计算电生理学
计算电生理学方法(CompEL, Computational Electrophysiology)[135]可用于模拟穿过膜通道的离子流, 这些离子流是由跨膜电位或离子浓度梯度驱动的. 就像在真正细胞中那样, CompEL中的跨膜电位是通过对穿过膜的电荷维持一个小的不平衡 \(\D q\) 实现的. \(\D q\) 和膜电容给出了电位差:
$$ \Delta U=\Delta q/C_{membrane} \tag{6.59}$$
跨膜电场与浓度梯度由.mdp选项控制, 允许用户设置膜每侧的参考离子数. 如果离子的实际数目与参考数目不同, 并且这种情况持续的时间超过了用户指定的时间, 程序会交换两侧的一些离子对或水对, 直至离子数目恢复到参考数目.
通过计算通道电导性与离子选择性, CompEL模拟也可用于确定通道的逆电位, 它是电生理实验中获得的重要表征参数.
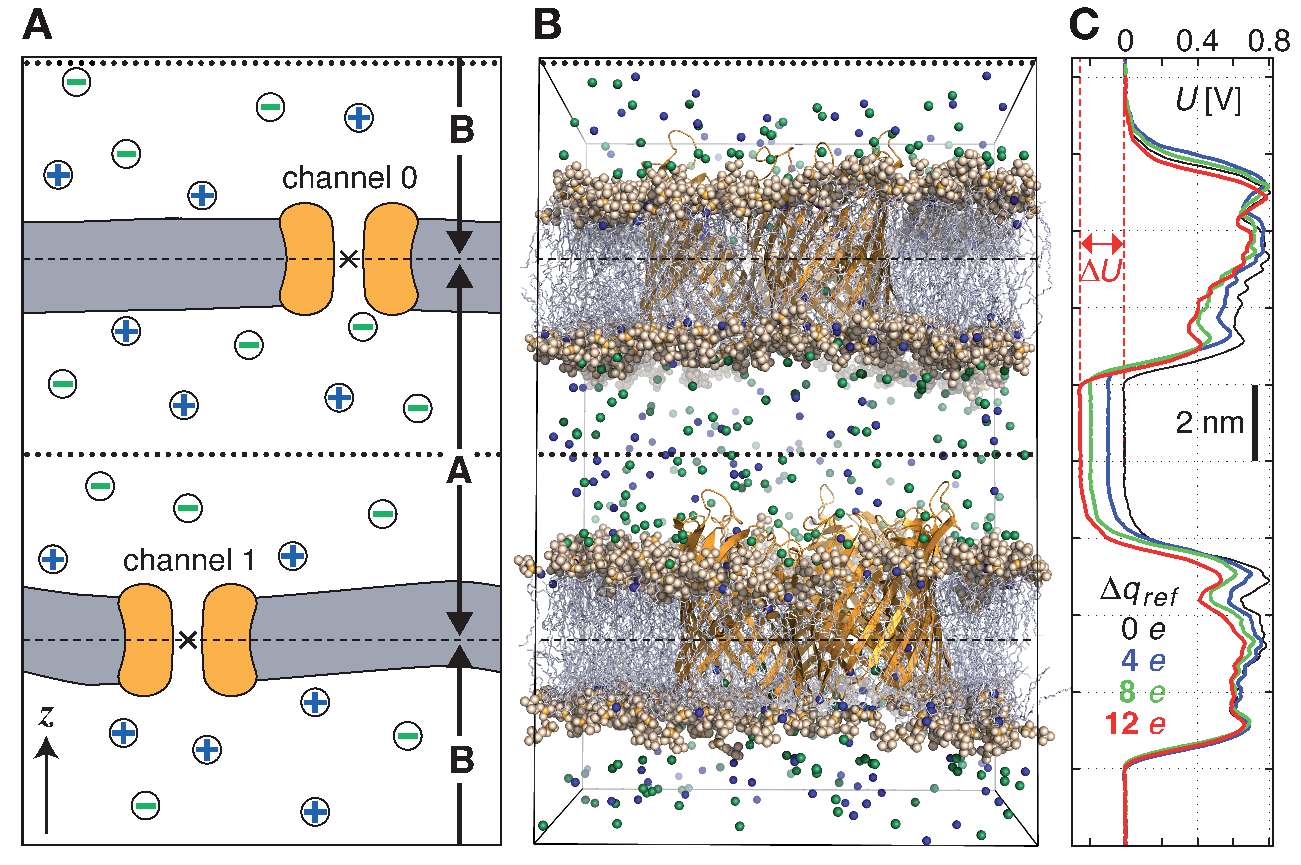
设置CompEL时, 模拟体系被划分为两个部分, A和B, 它们的离子浓度是独立的, 互不相关. 构建体系的最好方法是利用两个双层体系, 每个都包含感兴趣的通道/孔(图6.6 A, B). 若它们通道的轴方向相同, 这样就可以在正电位和负电位情况下同时观察到通道中的离子流, 这对一些研究, 如通道整流非常重要.
使用gmx potential工具可以很容易地计算跨膜电位差 \(\D u\). 这样在模拟的每个时间段都可以精确地得到沿 \(z\) 轴或孔轴的电势降低(图6.6 C). 在模拟中, 穿过通道的电荷为 \(q_i\) 的离子 \(i\) 的类型与数目都会写入swapions.xvg输出文件中. 利用此输出文件, 可确定在每个时间段 \(\D t\) 内的平均通道电导值 \(G\)
\[G={\S_i n_i q_i \over \Delta t \Delta U} \tag{6.60}\]
离子选择性可通过不同种类离子数流量的比值来计算. 要想得到最好的结果, 需要对许多重合时间段内的值进行平均.
逆电位的计算最好是利用一系列小的模拟, 每个模拟中使用较小但强度变化的离子不平衡来产生给定的跨膜浓度梯度. 例如, 若一侧含有1 M浓度的盐, 另一侧的浓度为0.1 M, 其余部分保持电荷中性, 可使用 \(\D q=0 e\), \(\D q=2 e\), \(\D q=4e\) 的一系列模拟. 对获得的零电流附近的所有 \(I-U\) 对, 利用电流电压关系进行线性拟合就可以得到 \(U_{rev}\).
6.6.1 使用
可利用如下的.mdp选项控制CompEL计算:
swapcoords = Z ; 交换位置 Swap positions: no, X, Y, Z
swap_frequency = 100 ; 尝试交换的频率 Swap attempt frequency
若你的膜位于 \(xy\) 平面内, 请选择Z(图6.6 A, B). 这样两侧之间的离子交换只依赖于 \(z\) 的位置. swap_frequency决定尝试交换的频繁程度, 进行交换时需要在并行队列之间通讯离子, 溶剂和交换组位置的信息, 若交换频率过高, 会降低运算速度.
split_group0 = channel0 ; 定义一侧边界 Defines compartment boundary
split_group1 = channel1 ; 定义另一侧边界 Defines other compartment boundary
massw_split0 = no ; 使用质量权重中心 use mass-weighted center?
massw_split1 = no
split_group0和split_group1为两个索引组, 用于定义两侧之间的边界, 通常是通道的中心. 若massw_split0或massw_split1设置为yes, 会使用每个索引组的质心作为边界, 在这里是 \(z\) 方向的质心. 否则将使用几何中心(图6.6中A中的×). 如果像这里一样, 一个膜通道被选作划分组, 其中心将定义两侧之间的分隔平面(图中的虚横线). 所有索引组都必须在索引文件中进行定义.
swap_group = NA+_CL- ; 交换离子 Ions to be included in exchange
solvent_group = SOL ; 溶剂分子的组名称 Group name of solvent molecules
cyl0_r = 5.0 ; 划分组孔半径 Split cylinder 0: pore radius (nm)
cyl0_up = 0.75 ; 上面延伸 Split cylinder 0 upper extension (nm)
cyl0_down = 0.75 ; 下面延伸 Split cylinder 0 lower extension (nm)
cyl1_r = 5.0 ; 其他通道设置 same for other channel
cyl1_up = 0.75
cyl1_down = 0.75
coupl_steps = 10 ; 两次平均之间的交换次数 Average over these many swap steps
threshold = 1 ; 若小于此值不进行交换 Do not swap if < threshold
swap_group设置了流和交换循环中所涉及离子的索引组, solvent_group定义了与离子互换的溶剂组. 圆柱选项只影响离子的计数, 即, 穿过通道0或1的离子会被计数, 计数时依据(通道)圆柱相对于各个划分组位置的半径的定义, 上下扩展. 这并不影响实际的流和交换, 却能提供离子穿过每个通道的次数. 注意, 只有当一个离子在互换步骤中 处于 定义的划分圆柱范围内时, 才能认为离子通过了某个特定的通道, 若swap_frequency太高, 特定的离子可能在一个互换步骤中处于A侧, 在下一步骤中却处于B侧, 因此就无法清楚地确定离子到底是穿过了哪个通道.
coupl_steps设置了尝试互换的步骤数, 也就是每侧中实际离子数与参考离子数之间的差距, 在实际交换发生以前必须尝试的次数. 若coupl_steps设置为1, 那么离子交换与否由瞬时离子分布决定, 而coupl_steps > 1时则由尝试步骤过程中时间平均的离子分布决定. 这适用于一些情况, 例如, 当离子扩散至两侧的边界时, 会导致大量无效的离子交换, threshold为1意味着进行交换时一侧的平均离子数与设定值至少相差1. 更高的阈值将导致更大容许差距. 离子将交换直至达到设定的数目 \(\pm\) 阈值.
anionsA = -1 ; A侧离子的参考数目 Reference count of anions in A
cationsA = -1 ; ... of cations in A
anionsB = -1 ; ... of anions in B
cationsB = -1 ; ... of cations in B
这些选项设定两侧需要的阴离子数与阳离子数. -1意味着它们的数目由0时间步的值决定, 并保持不变, 注意, 这些数目应加到互换组的总离子数中.
注意, CompEL模拟的双层体系, 可以很容易地使用下列方法创建. 利用gmx editconf -translate 0 0 <l_z>命令沿膜的法线方法(通常为 \(z\))重复已有的膜/通道MD体系, 其中l_z为重复方向的盒子长度. 如果你已经定义了单层体系通道的索引组, 使用gmx make_ndx -n index.ndx -twin可得到双层体系的索引组.
为抑制膜沿互换方向的大的涨落, 采用伞形牵引(参见6.4节)在两个通道和/或双层中心之间施加简谐势(仅作用于交换方向), 可能会有帮助.
多通道
如果划分组包含的分子数大于1, 必须正确地选择所有分子相对于彼此的PBC映象, 这样才能正确地确定通道中心. GROMACS假定.tpr文件中初始结构的PBC表示是正确的. 设定下面的环境变量可检查是否正确
GMX_COMPELDUMP: 分子完整后后将它的初始结构输出到.pdb文件.
6.7 使用自由能代码计算PMF
自由能耦合参数方法(参见3.12节)提供了几种计算平均力势的方式. 通过使用简谐势或约束连接两个原子, 可计算它们之间的平均力势. 为达到这个目的, 一些特殊的势能函数可避免产生额外的排除, 参见5.4节. 当状态B中的最小或约束长度比状态A中的大1 nm时, 限制力或约束力为 \(\partial H/\partial \l\). 通过设置.mdp文件中的delta-lambda可改变原子间的距离, 它是 \(\l\) 和时间的函数. 所得到的结果应当与使用伞形抽样或约束抽样得到的结果完全相同(尽管由于实现方法不同数值上不可能完全相同). 与牵引代码不同, 自由能代码也可用于处理约束连接的原子.
也可利用位置限制来计算平均力势. 采用位置限制时, 原子连接到空间中的某一位置, 二者之间具有简谐势(参见4.3.1节). 这些位置可以是耦合参数 \(\l\) 的函数. 可利用grompp的-r和-rb选项分别设置A状态和B状态的位置. 可以利用这种方法进行靶向MD. 注意, 我们并不鼓励对蛋白质使用靶向MD. 将这些构象作为状态A和B的位置限制坐标, 就可以强制蛋白质从一个构型转换到另一个. 你可以在0和1之间缓慢地改变 \(\l\) 的值. 这种方法的主要缺点在于, 蛋白质的构型自由度受到位置限制的严重制约, 而与从状态A到B的变化无关. 此外, 蛋白质由状态A到B的强制转变几乎处于一条直线上, 而实际的路径可能大为不同. 更适合这种方法的体系是固体体系或限制于边界或墙之间的液体. 你可以用这种方法来测量改变与边界或墙之间的距离时所需要的力. 因为边界(或墙)必须要固定. 位置限制并不会限制体系的抽样.
6.8 移除最快的自由度
MD模拟的最大时间步长由模拟体系中的最小振动周期决定. 键伸缩振动处于量子力学基态, 因此利用约束进行描述比简谐势更好.
对其余的自由度, 最短振动周期(模拟所得)是13 fs, 涉及氢原子键角的振动. 作为一项准则, 使用Verlet(蛙跳式)积分方案时, 对一个简谐振子, 每个周期内至少需要执行5次数值积分步才能达到合理的精度, 相应的最大时间步长约为3 fs. 忽略这些非常快的周期为13 fs的振动, 下一个最短的周期约为20 fs, 相应的最大时间步长约为4 fs.
从氢原子中移除键角自由度的最好方法是将它们定义为虚拟作用位点而不是常规原子. 常规原子通过键, 键角, 二面角连接到分子, 而虚拟位点的位置则根据已定义好的方式, 由三个邻近重原子的位置计算得到(参看4.7节). 对水, 羟基, 巯基或氨基中的氢原子, 不能移除其自由度, 因为需要保留旋转自由度. 除此之外, 唯一可降低这些快速运动的方法是增加氢原子的质量, 但同时也需要增加与氢原子相连的重原子的质量. 这会增大水分子, 羟基, 巯基或氨基的转动惯量, 但不会影响体系的平衡性质, 对体系动力学性质的影响也不会太大. 这些方法将在6.8.1节进行简短的讨论, 以前的论文中有详细的讨论[136].
使用虚拟位点并同时修改质量, 下一瓶颈可能是由不当二面角(用于维持分子基团的平面性或手性)和肽的二面角引起. 不可能更改肽的二面角而不影响蛋白质的物理行为. 维持平面性的不当二面角主要用于处理芳香残基, 这些残基中的键, 键角, 二面角也可以替换为稍复杂点的虚拟位点.
本节所讨论的所有修改都可以使用GROMACS的拓扑创建工具pdb2gmx来完成, 其中有单独的选项用于增加氢原子的质量, 虚拟化所有氢原子或虚拟化所有芳香残基. 注意, 当全部氢原子都被虚拟化后, 那些处于芳香残基内部的氢原子也将被虚拟化, 即, 对芳香残基中氢原子的处理各不相同, 而是取决于对芳香残基的处理.
当处理拓扑文件时, grompp会直接从力场参数(键长和键角)中获取氢原子虚拟位点的构建参数. 对芳香残基, 这些构建方法基于力场中结构的键长, 键角, 但这些参数是直接写入pdb2gmx源代码中的, 因为对整个芳香基团的构建非常复杂.
6.8.1 氢原子的键-键角振动
构建虚拟位点
将氢原子定义为虚拟位点的目的在于去除所有的高频自由度. 在一些情况下, 不应该去除所有的氢原子自由度, 例如对羟基或氨基应当保留氢原子的旋转自由度. 必须注意构建虚拟位点时不能引入不需要的相关, 例如构建原子间的键-键角振动可能会转变为氢原子的键振动. 另外, 由于虚拟位点没有质量, 根据定义, 为了维持体系的总质量守恒, 被视为虚拟位点的氢原子的质量应当加到与其相连接的重原子上.
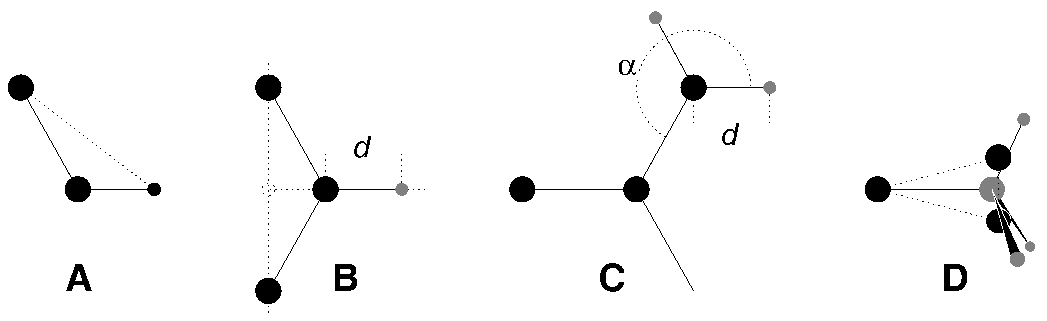
考虑到这些, 蛋白质中的氢原子可以自然地分为几类, 每一类需要不同的构建方法(参见图6.7).
羟基(-OH)或巯基(-SH)氢原子: 羟基中唯一可约束的内部自由度为C-O-H键角. 通过定义一个额外的具有适当长度的键可对此键角进行固定, 见图6.7 A. 这样可以去除键角弯曲的高频振动, 同时保留了二面角的旋转自由度. 对巯基情况相同. 注意, 在这种情况下氢原子并不被视为虚拟位点.
单个氨基或酰胺(-NH-)和芳香氢原子(-CH-): 不能利用键矢量的线性组合来构建这些氢原子的位置, 因为重原子之间具有柔性的键角. 作为替代, 可将氢原子置于与重原子距离固定的位置, 位于通过成键重原子与两个第二键合原子连线上一点的直线上, 见图6.7 B.
平面氨基(-NH2)氢原子: 用于单个酰胺氢原子的方法用于平面氨基时效果不好, 因为找不到两个合适的重原子来定义氢原子的方向. 作为替代, 氢原子被置于距N原子一定距离的位置, 与C原子所成的键角固定, 处于其他重原子定义的平面上, 键图6.7 C.
氨基(伞形 -NH2或-NH3+)氢原子: 不能由与其相连的重原子来构建具有旋转自由度的氨基氢原子的虚拟位点, 因为这样做会失去氨基的旋转自由度. 为保留旋转自由度同时去除氢原子的键-键角自由度, 可构建两个“哑质点”, 它们具有与氨基相同的总质量, 转动惯量(绕C-N键转动)和质心. 这些哑质点原子与任何其他原子都不存在相互作用, 它们会彼此相连, 且与碳原子相连, 形成刚性三角形. 由这三个粒子, 可根据两个碳原子的矢量及其外积的线性组合来构建N和氢原子的位置, 这样得到的氨基具有旋转自由度, 但不含其他内部自由度, 见图6.7 D.
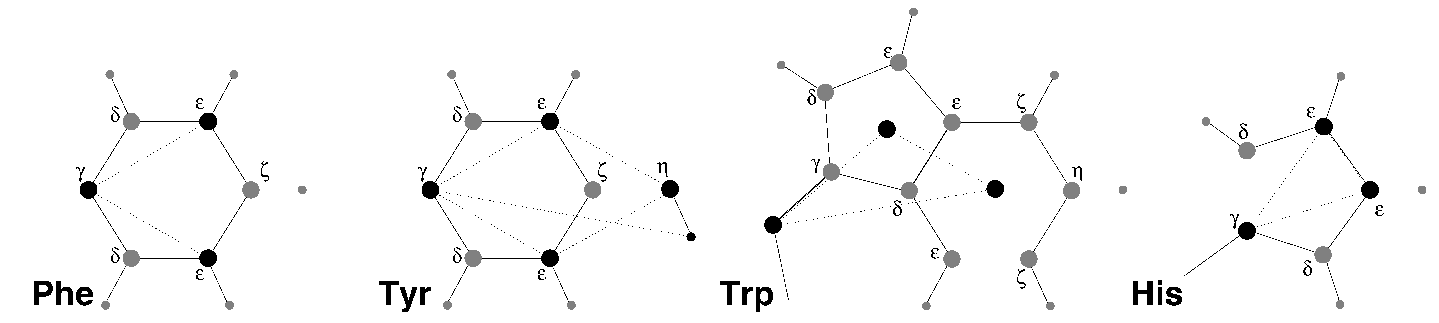
6.8.2 芳香基团的面外振动
芳香残基支链中的平面结构致使它自身就是一个完美的虚拟位点的构建方式, 具有完美的平面基团, 没有本质上不稳定的, 用于维持正常原子处于平面内所需要的约束. 构建的基本方法是定义三个原子或哑质点, 利用三者相互之间的约束来固定几何结构, 并将其余原子作为简单的虚拟位点类型(参见4.7节). 不同的芳香残基需要不同的方法:
- 苯丙氨酸: \(\text{C}_\g\), \(\text{C}_{\e1}\), \(\text{C}_{\e2}\) 作为正常原子, 但每个的质量为苯基的1/3, 见图6.8 A.
- 络氨酸: 对苯环的处理与苯丙氨酸相同. 另外, 在 \(\text{C}_{\e1}\), \(\text{C}_{\e2}\) 和 \(\text{C}_\h\) 之间定义约束. 原始的不当二面角可将两个三角形(一个为苯环的, 一个与 \(\text{C}_\h\) 有关)维持在平面内, 但由于转动惯量更大, 约束更稳定. 羟基中的键-键角使用 \(\text{C}_\g\) 和 \(\text{C}_\h\) 之间的约束进行约束. 注意, 氢原子并不视为虚拟位点进行处理, 见图6.8 B.
- 色氨酸: 将 \(\text{C}_\b\) 视为常规原子, 在每个环的质心创建两个哑质点, 每个的质量等于相应环的总质量(\(\text{C}_{\d2}\) 和 \(\text{C}_{\e2}\) 对每个环的贡献为1/2). 这样做可以保持总质量和转动惯量几乎等于原本的值, 见图6.8 C.
- 组氨酸: 将 \(\text{C}_\g\), \(\text{C}_{\e1}\), \(\text{N}_{\e2}\) 视为正常原子, 但其质量会重新分配, 这样环的质心保持不变, 见图6.8 D.
6.9 粘度计算
剪切粘度是液体的一种性质, 实验上很容易测量. 它可用于力场的参数化, 因为它是一个动力学性质, 而用于力场参数化的大多数其他性质都是热力学性质. 粘度也是一种重要的性质, 因为它会影响液体中溶剂化分子的构象变化的速率.
利用爱因斯坦关系式可以从平衡模拟计算粘度:
\[\h ={1\over2} {V \over k_BT} \lim_{x\to \infty} {\rmd{} \over \rmd t} \left\langle \left( \int_{t_0}^{t_0+t} P_{xz}(t') \rmd t' \right)^2 \right\rangle_{t_0} \tag{6.61}\]
这可以利用g_energy进行计算. 这种方法收敛十分缓慢[137], 用于确定粘度的精确值时, 即便是纳秒尺度的模拟也可能不够长. 此外, 计算结果非常依赖于对静电的处理. 使用(短的)截断会导致压力的非对角元素出现很大噪声, 可能使计算的粘度值增大一个数量级.
GROMACS也提供了计算粘度的非平衡方法[137]. 其原理基于以下事实, 通过外力输入体系的能量会通过粘性摩擦而耗散, 产生的热会通过耦合的热浴移除. 对牛顿流体, 施加一个小的力会导致速度梯度, 其方程如下:
$$ a_x(z)+{\h \over \r} \oppar{v_x(z)} z=0 \tag{6.62}$$
这里我们在 \(x\) 方向施加了加速度 \(a_x(z)\), 它是坐标 \(z\) 的函数. 在GROMACS中加速的的剖面为:
\[a_x(z)=A\cos \left( {2\p z \over l_z}\right) \tag{6.63}\]
其中为 \(l_z\) 为盒子的高度. 产生的速度剖面为:
\[v_x(z)=V\cos \left({2\p z \over l_z} \right) \tag{6.64}\]
\[V=A {\r \over \h} \left( {l_z \over 2\p} \right)^2 \tag{6.65}\]
可利用 \(A\) 和 \(V\) 来计算粘度:
\[\h ={A \over V}\r \left( {l_z \over 2\p} \right)^2 \tag{6.66}\]
模拟中 \(V\) 的定义为
\[V={\Sum_{i=1}^N m_i v_{i,x}^2\cos \left({2\p z \over l_z} \right) \over \Sum_{i=1}^N m_i } \tag{6.67}\]
产生的速度剖面并不耦合到热浴. 此外计算体系动能时会排除速度剖面. 你可能希望使用尽可能大的 \(V\) 以得到好的统计, 但剪切速率不能太高, 以免使体系过远地远离平衡态. 当余弦为零时, 剪切速率最大,
\[\text{sh}_{\max} =\underset{z}{\max} \left| \opar{v_x(z)} z \right|=A {\r \over \h} {l_z \over 2\p} \tag{6.68}\]
对 \(\h = 10^{-3}\) [kg m-1 s-1], \(\r=10^3\) [kg m^–3], \(l_z = 2\p\) [nm]的模拟, \(\text{sh}_\max=1\) [ps nm-1] \(A\). 这个剪切速率应小于体系中最长相关时间的倒数. 对大多数液体, 转动的相关时间最长, 大约为10 ps. 对上面的情况, \(A\) 应小于0.1 [nm ps-2]. 若剪切速率过高, 观察到的粘度会过低. 由于 \(V\) 正比于盒子高度的平方, 盒子最好沿 \(z\) 轴方向延伸. 一般而言, 要得到粘度的精确值, 100 ps的模拟长度足够了.
由粘性摩擦产生的热会被耦合热浴移除. 由于这种耦合并不是瞬时的, 液体的真正温度会稍稍低于观察到的温度. Berendsen推导了这种温度偏移[30], 它与剪切速率的关系为:
\[T_s={\h \t \over 2 \r C_v} \text{sh}_\max^2 \tag{6.69}\]
其中 \(\t\) 为Berendsen控温器的耦合时间, \(C_v\) 为热容. 使用上面例子中的值, \(\t=10^{-13}\) [s], \(C_v=2 \cdot 10^3\) [J kg-1K-1], 可得到 \(T_s=25\) [K ps-2] \(\text{sh}_\max^2\), 如果需要的剪切速率小于 \(1/10\) [ps-1], \(T_s\) 小于0.25 [K], 可忽略不计.
注意, 当从平衡态开始时, 体系必须要构建速度剖面, 构造所需时间的数量级与液体的相关时间一致.
根据方程6.66得到的 \(V\) 和 \(1/\h\) 这两个量及其平均值与涨落会写入到能量文件.
6.10 表格相互作用函数
6.10.1 势能三次样条插值
在GROMACS的一些内部循环中, 计算势能与力时会使用查表的方法, 并利用三次样条算法对这些表格进行插值. 对静电, 色散, 排斥相互作用会使用独立的表格, 但为了提高缓存性能, 这些项被合并到一个单一的数组中. 对 \(x_i \le x \lt x_{i+1}\) 的三次样条插值为:
\[V_s(x)=A_0+A_1 \e +A_2 \e^2+A_3 \e^3 \tag{6.70}\]
其中表格间距 \(h\) 与分数 \(\e\) 为:
\[\alg h &=x_{i+1}-x_i \tag{6.71} \\ \e &= (x-x_i)/h \tag{6.72} \ealg\]
因此 \(0 \le \e \lt 1\). 由此, 我们可以计算导数得到力:
\[-V_s'(x)=- {\rmd {V_s(x)} \over \rmd \e} {\rmd \e \over \rmd x}=-(A_1+2A_2 \e+3 A_3\e^2)/h \tag{6.73}\]
四个系数可以从四个条件得到: \(V_s\) 和 \(-V_s'\) 在每个区间的两端应精确地等于势能 \(V\) 与力 \(-V'\) 的值. 这样得到了每个区间上的误差
\[\alg |V_s-V|_\max &=V'''' {h^4 \over 384}+O(h^5) \tag{6.74} \\ |V_s'-V'|_\max &=V'''' {h^3 \over 72 \sqrt 3} +O(h^4) \tag{6.75} \\ |V_s''-V''|_\max &=V'''' {h^2 \over 12}+O(h^3) \tag{6.76} \ealg\]
\(V\) 和 \(V'\) 连续, 但 \(V''\) 一阶不连续. 对混合精度与双精度的GROMACS, 每纳米的点数分别为500和2000. 这意味着势能与力的误差通常小于混合精度的精确度.
GROMACS会存储 \(A_0\), \(A1\), \(A_2\) 和 \(A_3\). 计算力的子程序会获得一个具有这些参数与缩放因子 \(s\) 2的表格, \(s\) 等于每nm的点数(注意 \(h\) 的单位为 \(s^{-1}\)). 算法的过程大致如下:
- 计算距离向量(\(\bi r_{ij}\))与距离 \(r_{ij}\)
- 将 \(r_{ij}\) 乘上 \(s\), 截断到整数值 \(n_0\) 以获得表格中的索引号
- 计算分数部分(\(\e=s r_{ij}-n_0\))与 \(\e^2\)
- 利用插值计算势能 \(V\) 与标量力 \(f\)
- 将 \(f\) 乘上 \(\bi r_{ij}\), 得到矢量力 \(\bi F\)
注意 查表明显 慢于 大部分Lennard-Jones与库仑相互作用的计算. 然而, 它比PPPM方法中使用的移位库仑函数要快很多. 最后, 修改一个势能的表格(得到它的图形表示)要比修改MD程序中的内部循环简单得多.
6.10.2 用户自定义势能函数
你也可以使用自己的势能函数而无需编辑GROMACS的源代码. 势能函数应符合下面的方程
\[V(r_{ij})={q_i q_j \over 4\p \e_0} f(r_{ij})+C_6 g(r_{ij})+C_{12} h(r_{ij}) \tag{6.77}\]
其中 \(f\), \(g\), \(h\) 为用户自定义的函数. 注意 若 \(g\) 代表正常的色散相互作用, \(g(r)\) 应 <0. \(C_6\), \(C_{12}\) 和电荷由拓扑读入. 也要注意组合规则只支持Lennard-Jones与Buckingham势能函数, 你的表格应匹配二进制拓扑中的参数.
当在你的.mdp文件中添加下面的行时,
rlist = 1.0
coulombtype = User
rcoulomb = 1.0
vdwtype = User
rvdw = 1.0
mdrun将将读入一个非键相互作用表格文件, 若设置了energygrp-table则将读入多个非键相互作用文件(参见下面的说明). 文件的名称可使用mdrun的选项-table设置. 表格文件应包含7列用于查询的数据, 依次为: \(x\), \(f(x)\), \(-f'(x)\), \(g(x)\), \(-g'(x)\), \(h(x)\), \(-f'(x)\). \(x\) 的范围从0到 \(r_c+1\)(table_extension的值可在.mdp文件中更改). 可以选择你喜欢的间距. 对标准表格, GROMACS对混合精度与双精度分别使用了0.002与0.0005 nm. 在这里, \(r_c\) 表示两个截断rvdw和rcoulomb的最大值(参见上文). 这些变量不需要相同(也不需要为1.0). 一些用作势能的函数在 \(x=0\) 处存在奇点, 但由于原子彼此之间的距离通常不会小于0.1 nm, \(x=0\) 处的函数值并不重要. 最后, 也可以将标准的库仑和修改的LJ势组合在一起(反之亦然), 只须指定, 例如coulombtype = Cut-off或coulombtype = PME, vdwtype = User. 但表格文件必须始终包含7列, 并且所有列中必须为有意义的数据(不能为零). 你可以在GMXLIB目录中找到一些创建好的表格文件, 它们可用于6–8, 6–9, 6–10, 6–11和6–12 Lennard-Jones势, 并使用了正常的库仑相互作用.
如果想对不同原子组使用不同的函数形式, 可利用能量组进行设置. 利用.mdp的energygrp-table选项(参见7.3节)可以对不同的两个能量组之间的非键相互作用使用不同的表格. 具有不同相互作用势的原子应放于不同能量组中. 对于列于energygrp-table中的能量组对, 会使用正常的表格. 当需要对许多原子类型使用不同的函数形式时, 这种作法更简单一些,
6.11 混合量子经典模拟技术
在分子力学(MM)力场中电子的影响是利用经验参数进行描述的. 这些参数是基于实验数据得到的, 或是基于高水平的量子化学计算得到的, 对给定共价结构的基态适用. MM近似对基态过程通常足够精确, 在这些过程中原子间所有的键合连接都不会改变. 然而对那些键合连接会改变的过程, 例如化学反应过程或涉及多个量子态的过程, 如光化学转换, 不可忽略电子, 因此需要利用量子力学描述体系, 或是至少需要对体系中反应的那部分用量子力学进行描述.
模拟溶液中或酶中化学反应的一种方法是将量子力学(QM)与分子力学(MM)组合起来, 反应部分使用量子力学方法描述, 同时其余部分以力场描述. 目前的GROMACS版本中提供了几个流行量子化学程序的接口(MOPAC[138], GAMESS-UK[139], Gaussian[140] and CPMD[141]).
在GROMACS中两个体系之间的相互作用可以Field等人的方法[142]或Morokuma及其合作者的QM/MM方法[143, 144]进行描述.
6.11.1 概述
在本版本的GROMACS中可采用两种方法描述QM和MM两子体系之间的相互作用:
电子嵌入 QM子体系的哈密顿量包含了QM区域的电子与MM原子之间, QM原子核与MM原子之间的静电相互作用:
\[H^{QM/MM}=H_e^{QM}-\Sum_i^n \Sum_J^M {e^2 Q_J \over 4\p \e_0 r_{iJ} }+\Sum_A^N \Sum_J^M {e^2 Z_A Q_J \over e \p \e_0 R_{AJ} } \tag{6.78}\]
其中 \(n\) 和 \(N\) 分别为QM区域中的电子数与原子核数, \(M\) 为带电的MM原子数. 上式右边的第一项为孤立QM体系原始的哈密顿量. 两个加和项的第一个为QM电子与MM原子之间总的静电相互作用, 第二个为QM原子核与MM原子之间总的静电相互作用. QM原子与MM原子之间的键合相互作用在MM水平以合适的力场项进行描述. 连接两个子体系之间的化学键使用氢原子进行封端, 以保证QM区域的原子价层完整. 这类原子上的力只出现于QM区域, 但会分配到成键的两个原子上. 封端原子通常被称为链接原子.
ONIOM 在这种方法中, 首先会以需要的从头算水平计算孤立QM子体系的能量与梯度, 接下来会使用MM力场方法计算包含QM区域在内的整个体系的能量与力, 并将其加到前一步计算得到的能量与力中. 最后, 因为对QM区域内的相互作用考虑了两次, 为进行校正, 会使用分子力学对孤立的QM子体系进行计算, 并从上一步的结果中减去所得的能量与力. 总的QM/MM能量的计算表达式如下(梯度类似):
\[E_{tot}=E_I^{QM}+E_{I+II}^{MM}-E_I^{MM} \tag{6.79}\]
其中下标I和II分别代表QM和MM子体系. 上标代表了计算能量的水平. ONIOM方案的优点在于它并不限于两层QM/MM描述, 而是很容易推广到多层, 每一层都可以使用不同水平的方法进行描述.
6.11.2 使用方法
要使用GROMACS的QM/MM功能, 你需要:
- 如果需要, 引入QM/MM边界上的链接原子;
- 指定哪些原子需要在QM水平进行处理;
- 指定QM水平, 基组, QM界面的类型等等.
添加链接原子
对连接QM和MM子体系的键需要引入链接原子. 在GROMACS中, 链接原子具有特殊的原子类型, LA. 在QM计算中, LA原子类型被当作氢原子进行处理, 在力场计算中则被视为虚拟位点. 如果存在链接原子, 它们是体系的一部分, 但与其他任何原子都没有相互作用, 除了作用于其上的力会分配到成键的两个原子上. 在拓扑中, 链接原子(LA)因此被定义为虚拟位点原子.
[ virtual_sites2 ]
LA QMatom MMatom 1 0.65
关于虚拟位点的处理细节请参看5.2.2节. 在模拟的每一步, 链接原子会被取代.
另外, 键本身也会被约束代替:
[ constraints ]
QMatom MMatom 2 0.153
注意, 因为在我们的体系中, QM/MM键是碳碳键(0.153 nm), 我们使用的约束长度为0.153 nm, 哑位置为0.65. 后者为理想碳氢键长与理想碳碳键长之间的比例. 采用这一比例, 链接原子始终距离QMatom0.1 nm, 与碳氢键长相符. 如果QM和MM子体系由不同类型的键相连接, 需要使用与键类型匹配的不同约束与哑位置.
指定QM原子
需要在QM水平处理的原子, 包括链接原子, 要添加到索引文件中. 此外, QM区域中原子之间的化学键需要在拓扑文件中定义为连接键(键类型5):
[ bonds ]
QMatom1 QMatom2 5
QMatom2 QMatom3 5
指定QM/MM模拟参数
在.mdp文件中下列参数控制QM/MM模拟的运行.
QMMM = no
如果设为yes, 进行QM/MM模拟. 可以使用不同水平的QM单独对几个组进行描述, 在QMMM-grps域中指定这些组, 彼此之间以空格隔开. 各个组使用的从头算方法的水平在QMmethod和QMbasis域中指定. 使用不同水平的方法对组进行描述只能与ONIOM QM/MM一起使用, 由QMMMscheme指定.
QMMM-grps =:
使用QM水平描述的组
QMMMscheme = normal
可用选项为normal和ONIOM, 用于选择QM/MM接口. normal意味着QM子体系电子化的嵌入MM子体系中, 只能对一个QMMM-grps使用从头算方法进行描述, 方法的水平通过QMmethod和QMbasis指定. 体系的其余部分处于MM水平. QM和MM两个子体系的相互作用如下: MM部分的点电荷包含在QM部分的单电子哈密顿量中, 所有的Lennard-Jones相互作用都在MM水平进行描述. 如果选择ONIOM, 使用Morokuma及其同事发展的ONIOM方法对子体系之间的相互作用进行描述. 可以有一个以上的QMMM-grps, 每个组可以使用不同级别的QM(QMmethod和QMbasis)进行描述.
QMmethod =
用于计算QM原子的能量和梯度的方法. 可用的方法包括AM1, PM3, RHF, UHF, DFT, B3LYP, MP2, CASSCF, MMVB和CPMD. 对CASSCF, 电子数和活化空间的轨道数分别由CASelectrons和CASorbitals指定. 对CPMD, 平面波截断由关键词planewavecutoff指定.
QMbasis =
用于展开电子波函数的高斯基组. 目前只可使用高斯基组, 即STO–3G, 3–21G, 3–21G, 3–21+G, 6–21G, 6–31G, 6–31G, 6–31+G和6–311G. CPMD使用平面波展开而不是以原子为中心的基函数, planewavecutoff关键词控制平面波展开.
QMcharge =
QMMM-grps的总电荷数, 以e为单位. 在有一个以上QMMM-grps的情况下, 需要单独指定每个ONIOM层的总电荷.
QMmult =
QMMM-grps的多重度. 在有一个以上QMMM-grps的情况下, 需要单独指定每个ONIOM层的多重度.
CASorbitals =
进行CASSCF计算时包含在活化空间中的轨道数.
CASelectrons =
进行CASSCF计算时包含在活化空间中的电子数.
SH = no
若设为yes, 在激发态势能面进行QM/MM的MD模拟, 在模拟过程中, 当体系碰到锥形交叉线时, 强制非绝热跳跃到基态. 此选项只能与CASSCF方法联合使用.
6.11.3 输出
QM计算所得的能量与力会加到GROMACS计算的能量与力中, 在.edr文件中会有总QM能量的选择项.
6.11.4 未来发展
为增加QM/MM接口的精度, 一些功能目前正在开发中. 其中的一个功能是在QM计算中使用离域化的MM电荷. 使用这种模糊电荷的最大好处是库仑势在原子间距离时具有有限值. 在点电荷表示中, 靠近QM区域的部分带电的MM原子倾向于“过极化”QM体系, 在计算中会导致假象.
此外, 还需要发展一个过渡态优化方法.
6.12 自适应分辨率方案
自适应分辨率方案(AdResS)[145, 146]采用力插值方法将不同分辨率的两个部分耦合起来. 与前一节的混合经典量子模拟技术相反, 在AdResS中, 高分辨粒子的数目不固定, 可随着模拟时间而变化..
下面我们讨论的AdResS对相同体系采用双分辨描述(原子与粗粒), 示意图见图6.9. 本节的详细实现细节已发表于[147, 148].
每个分子需要一个定义良好的映射点(通常为质心), 但也可以使用粒子坐标的任何其他线性组合. 在拓扑中映射点被定义为虚拟位点. 粗粒化区域的力只是映射点位置的函数. 在这个实现中, 利用电荷组或电荷组的集合对分子进行建模, 这实际上允许一个分子有多个映射点. 对更大的分子, 如聚合物, 这种方法可能会有帮助. 在那种情况下, 必须扩展AdResS以描述键合相互作用[149]. 将来的GROMACS版本中会实现这种功能.
两个分子间的力为[145][1]:
\[\vec F_{\a\b} =w_\a w_\b \vec F_{\a\b}^\text{ex,mol}+[1-w_\a w_\b] \vec F_{\a\b}^\text{cg,mol} \tag{6.80}\]
其中 \(\a\) 和 \(\b\) 标记两个分子, \(w_\a\), \(w_\b\) 为两个分子的自适应权重.
上式第一部分代表了分子显式的相互作用, 可写为
\[\vec F_{\a\b}^\text{ex,mol}=\Sum_{i\in \a} \Sum_{i\in\b} \vec F_{ij}^\text{ex} \tag{6.81}\]
其中 \(\vec F_{ij}^\text{ex}\) 为第 \(\a\) 个分子中的第 \(i\) 个原子与第 \(\b\) 个分子中第 \(j\) 个原子之间的力, 由显式的力场给出. 方程6.80的第二部分来自分子的粗粒化相互作用. GROMACS中的实现稍有扩展:
\[\vec F_{\a\b}=\Sum_{i\in \a} \Sum_{i\in\b} w_i w_j \vec F_{ij}^\text{ex} +[1-w_\a w_\b] \vec F_{\a\b}^\text{cg,mol} \tag{6.82}\]
其中 \(w_i\) 和 \(w_j\) 为基于原子的权重, 由adress-site选项决定. 若adress-site为质心, 原子 \(i\) 具有其 电荷组 质量中心的权重, 分子 \(\a\) 的权重 \(w_\a\) 由粗粒化粒子的位置决定, 而粗粒化粒子由拓扑中指定的原子化粒子的虚拟位点构建. 这种推广可以实现各种AdResS方法, 同时普通的方法可利用拓扑中的质心虚拟位点, 设定adress-site=COM并把一个分子的所有原子(除代表粗粒化相互作用的虚拟位点外)放于同一电荷组来实现. 对大的分子, 使用基于原子的权重有时更好, 这可利用设置adress-site=atomperatom或将每个原子置于独立的电荷组(一个原子的电荷组质心为其自身)来实现.
粗粒化力场 \(\vec F^\text{cg}\) 通常利用基于结构的粗粒化方法由原子化体系导出(参见4.10.5节). 为指定哪些原子属于一个粗粒化表示, 可使用能量组. 每个粗粒化相互作用必须与单独的能量组相联系, 这就是代表粗粒相互作用的虚拟位点也必须处于不同电荷组的原因. 被视为粗粒化相互作用进行处理的电荷组, 列于adress_cg_grp_names. 插值的最重要内容(参见方程6.80和方程6.82)是自适应权重函数(示意图见图6.9):
\[w(x)=\begin{cases} \begin{array}{cl} 1 & : \text{原子化/显式区域 atomistic/explicit region} \\ 0 \lt w \lt 1 & : \text{杂合区域 hydrid region} \\ 0 & : \text{粗粒化区域 coarse-grained region} \end{array} \end{cases} \tag{6.83}\]
它的值处于0和1之间. \(w\) 的定义在显式区域是纯的显式力, 在粗粒化区域则是单纯的粗粒化力, 因此方程6.80中基本上只在杂合区域具有混合的相互作用, 这在标准模拟中是不会出现的. 在GROMACS中, 类似于cos2函数被用于权重函数:
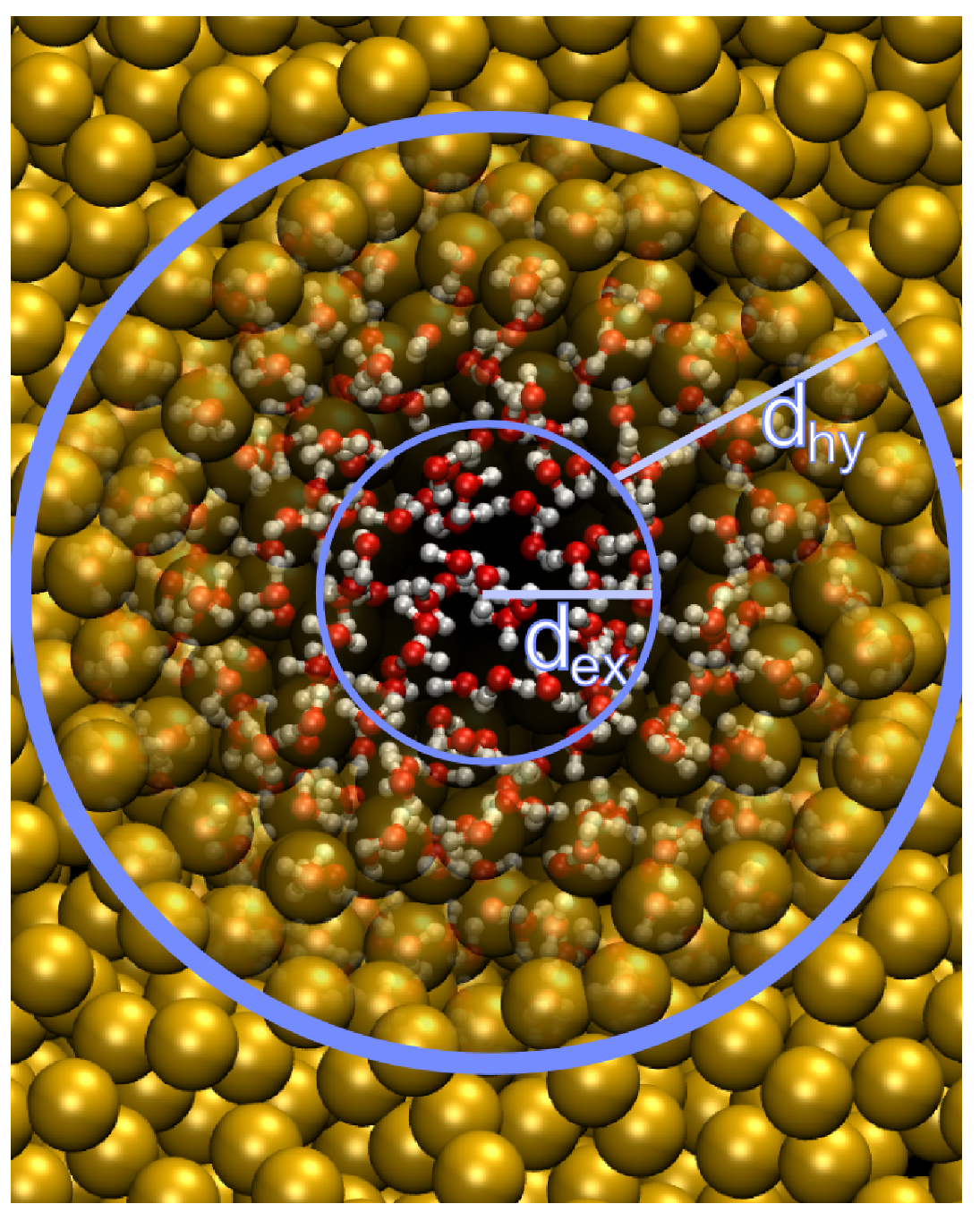
\[w(x)=\begin{cases} \begin{array}{ccl} 0 &: &\phantom{d_\text{ex}+d_\text{hy}>{} } x>d_\text{ex}+d_\text{hy} \\ \cos^2 \left({\p\over 2d_\text{hy} }(x-d_\text{ex})\right) &: &d_\text{ex}+d_\text{hy} >x>d_\text{ex} \\ 1 &: &\phantom{d_\text{ex}+{} }d_\text{ex} >x \end{array} \end{cases} \tag{6.84}\]
其中 \(d_\text{ex}\) 和 \(d_\text{hy}\) 分别为显式与杂合区域的大小. 根据研究体系的物理特点, 你也可以使用其他函数, 只要它们满足下面的边界条件: 1) 连续, 2) 单调, 3) 边界处导数为零. 已经实现了对模拟盒子的球形划分和一维划分(adress-type选项), 取决于此选项, 到显式中心的距离 \(x\) 的计算方法为:
\[x=\begin{cases} \begin{array}{cl} |(\vec R_\a - \vec R_\text{ct}) \cdot \hat e| &: 沿\hat e方向划分\; \text{splitting in}\ \hat e\ \text{direction} \\ |\vec R_\a - \vec R_\text{ct}| &: 球形划分\ \text{spherical splitting} \end{array} \end{cases} \tag{6.85}\]
其中 \(R_\text{ct}\) 为显式区域的中心(由adress-reference-coords选项定义), \(\vec R_\a\) 为第 \(\a\) 个分子的映射点. 对质心映射,
\[R_\a ={\sum_{i\in \a} m_i r_i \over \sum_{i\in \a} m_i} \tag{6.86}\]
注意, 权重函数的值唯一地取决于分子的映射. 力的插值(见方程6.82)可导致密度的非均匀性并影响杂合区域的体系结构.
减小密度不均匀性的一种方法是使用所谓的热力学力(TF, thermodynamic force)[151]. 这个力包含了空间相关的外场, 施加到杂合区域中每个分子的粗粒化位点上. 可以为体系中的每个物种指定这种力. TF补偿了在均相密度剖面中出现的压力剖面[152], 因此可以校正杂合区域中的局部密度不均匀性, 并允许原子化和粗粒化的部分之间相互耦合, 它们在构建时在目标密度具有不同的压力. 场的强度可以使用迭代过程确定, 详细说明见VOTCA软件包的手册[122]. 将adress-interface-correction设为thermoforce可启用TF校正, adress-tf-grp-names定义了校正作用的能量值.
6.12.1 例: 水的自适应分辨率模拟
本节将解释说明水的自适应分辨率模拟的设置, 模拟时原子化的SPC水模型[181]和它的粗粒化表示进行了耦合(如[152]中所用的). 为进行模拟需要下面一些步骤:
- 执行参考的全原子模拟
- 创建粗粒化表示并保存为表格相互作用函数
- 创建SPC水的杂合拓扑
- 修改原子坐标文件以包含粗粒化表示
- 在
grompp输入文件中定义分辨率模拟的构型 - 创建索引文件
相互作用粗粒化表示被存储为表格相互作用函数, 这种函数的说明见6.10.2节. 约定是使用 \(C^{(12)\) 列, 且系数 \(C^(12)\) 设为1, 其他所有列都为零. VOTCA手册中关于如何使用各种技术对SPC水进行粗粒化有详细的说明及教程. 这里, 我们将粗粒化相互作用命名为CG, 因此相应的表格文件为table_CG_CG.xvg. 要创建拓扑文件, 你可以从原子的拓扑文件开始,(例如share/gromacs/top/oplsaa.ff/spc.itp). 我们在这里假定使用刚性水模型. 在VOTCA教程中文件被命名为hybrid_spc.itp. 与原子化拓扑的唯一不同在于额外的粗粒化虚拟位点:
[ moleculetype ]
; molname nrexcl
SOL 2
[ atoms ]
; nr type resnr residue atom cgnr charge mass
1 opls_116 1 SOL OW 1 -0.82
2 opls_117 1 SOL HW1 1 0.41
3 opls_117 1 SOL HW2 1 0.41
4 CG 1 SOL CG 2 0
[ settles ]
; OW funct doh dhh
1 1 0.1 0.16330
[ exclusions ]
1 2 3
2 1 3
3 1 2
[ virtual_sites3 ]
; Site from funct a d
4 1 2 3 1 0.05595E+00 0.05595E+00
根据虚拟位点类型3及指定的系数, 虚拟位点位于分子的质心(对大分子必须使用virtual sitesn). 我们现在需要在拓扑文件中包含修改后的水模型并定义CG类型, 在topol.top中:
#include "ffoplsaa.itp"
[ atomtypes ]
;name mass charge ptype sigma epsilon
CG 0.00000 0.0000 V 1 0.25
#include "hybrid_spc.itp"
[ system ]
Adaptive water
[ molecules ]
SOL 8507
\(\s\) 和 \(\e\) 的值分别对应于 \(C_6=1\) 和 \(C_{12}=1\), 因此表格文件应该在 \(C_6\) 或 \(C_{12}\) 列包含粗粒相互作用. 在此列中我们使用了OPLS力场, 并指定了 \(\e\) 和 \(\s\). 注意, 对那些直接使用 \(C_6\) 和 \(C_{12}\) 项定义原子类型的力场, 可以简单地设置 \(C_6=0\) 和 \(C_{12}=0\). 关于表格相互作用的更多细节请参考6.10.2节. 由于水分子具有一个虚拟位点, 坐标文件也需要包括虚拟位点.
adaptive water coordinates
34028
1SOL OW 1 0.283 0.886 0.647
1SOL HW1 2 0.359 0.884 0.711
1SOL HW2 3 0.308 0.938 0.566
1SOL CG 4 0.289 0.889 0.646
1SOL OW 5 1.848 0.918 0.082
1SOL HW1 6 1.760 0.930 0.129
1SOL HW2 7 1.921 0.912 0.150
1SOL CG 8 1.847 0.918 0.088
(...)
此文件可手动创建或使用VOTCA工具csg_map的--hybrid选项创建.
在grompp输入文件中, 需要启用AdRess功能, 并定义构型.
(...)
; AdResS relevant options
energygrps = CG
energygrp_table = CG CG
; Method for doing Van der Waals
vdw-type = user
adress = yes
adress_type = xsplit
adress_ex_width = 1.5
adress_hy_width = 1.5
adress_interface_correction = off
adress_reference_coords = 8 0 0
adress_cg_grp_names = CG
在这里我们定义了能量组CG, 它包含了粗粒化的虚拟位点. 如前所述, 粗粒化相互作用通常使用表格, 这就要求将vdw-type设置为user. 若对多组分体系进行粗粒化, 必须为每一个组分定义一个能量组. 注意, 定义粗粒化表示的所有能量组, 都必须列于adress_cg_grp_names中, 以便与常规能量组区分开来.
必须更新索引文件, 并添加CG组, 其中包含所有粗粒化虚拟位点, 使用GROAMCS的工具make_ndx很容易完成.
6.13 VMD插件用于轨迹文件输入/输出
GROMACS可以使用已经安装的VMD插件来读写非GROMACS格式的轨迹文件. 例如, 你可以将AMBER DCD格式的轨迹文件直接提供给GROMACS工具.
要使用上述功能, VMD的版本不能低于1.8, 还需要你的系统提供dlopen函数, 这样才能在运行时确定存在哪些插件, 构建GROMACS时是否构建了共享库. CMake将会在你的路径下查找VMD可执行程序, 根据这个路径, 或者在配置或运行时的环境变量VMDDIR来定位插件. 作为替代, 运行时可利用VMD_PLUGIN_PATH来指定插件的路径. 注意, 这些插件是二进制形式的, 格式必须匹配插件所在机器的架构.
6.14 交互式分子动力学
GROMACS支持交互式的分子动力学(IMD, interactive molecular dynamics)协议, VMD可利用此协议控制NAMD中运行的模拟. IMD允许从VMD客户端监测正在运行的GROMACS模拟, 此外, 通过使用鼠标或力反馈设备拉扯原子, 残基或片段, 用户可以与模拟进行互动. 关于GROMACS实现及示例GROMACS IMD系统的额外的信息可以在这个主页上找到.
6.14.1 准备模拟输入
GROMACS的实现只允许与运行模拟的一部分进行传送与交互, 例如, 当没有水分子被传送或牵引的情况下. 通常使用.mdp文件的IMD-group选项指定组. 当IMD-group为空时, IMD协议被禁用, 不能通过mdrun的开关来启用. 要与整个体系进行互动, IMD-group可设为System. 当使用grompp时, 作为VMD输入的.gro文件会写出(grompp的-imd开关).
6.14.2 启动模拟
VMD与GROMACS之间的通讯可利用TCP套接字完成, 因而可控制本地机器或远程集群上的mdrun. 可利用mdrun的-imdport选项指定连接端口, 默认为8888. 如果指定的端口号为0或更小, GROMACS会自动为IMD分配一个可用的端口.
mdrun客户端每 \(N\) 步接收一次VMD中的力, 并将新的位置发送到客户端. VMD允许以交互方式增加或减小通讯频率. 默认情况下, 即使没有连接IMD客户端, 模拟也会启动并运行. 这种行为可利用mdrun的-imdwait开关选项更改. 启动后, 每当客户端断开连接时, 积分会停止直至重新连接客户端. 当使用-imdterm开关时, 可以通过按下VMD中的stop按钮来终止模拟, 默认未启用此功能. 最后, 为了与模拟进行互动, (即从VMD中牵引)必须使用-imdpull选项. 因此, 当未设置-imdwait, -imdterm或-imdpull时, 只可以监测模拟, 而不能从VMD客户端影响模拟. 然而, 由于IMD协议无须认证, 在不安全环境直接可连的主机上运行模拟是不明智的. TCP的安全shell转发可用于连接不能从活动主机直接可达的模拟. 注意, mdrun的IMD命令行开关默认是隐藏的, 只有使用gmx mdrun -h -hidden才能显示于帮助文本中.
6.14.3 从VMD中连接
在VMD中, 首先必须加载与IMD组对应的结构(File → New Molecule), 然后必须使用IMD的连接窗口((Extensions → Simulation → IMD Connect (NAMD)). 在IMD连接窗口中, 必须指定主机名与端口, 并点按下 connect 按钮, Detach Sim 允许断开连接, 同时不中断模拟, Stop Sim 会在下一次近邻搜索前终止模拟(若-imdterm运行).
时间步传输速率用于调整模拟与IMD客户端之间的通讯频率. 当接收到新的帧时, 设置保持速率每 \(N\) 帧加载到VMD一次而不是忽略它们. 显示的能量单位是国际单位, 与NAMD不同.
-
注意, 此方程服从牛顿第三定律, 而其他一些实现方案未必服从[150]. ↩
