本手册已过时, 不再更新. 如果需要最新手册, 请加入下方QQ群.
- 8.1 使用组
- 8.2 查看你的轨迹
- 8.3 通用性质
- 8.4 径向分布函数
- 8.5 相关函数
- 8.6 均方位移
- 8.7 键/距离, 键角和二面角
- 8.8 回旋半径与距离
- 8.9 结构的根均方偏差
- 8.10 协方差分析
- 8.11 二面角主成分分析
- 8.12 氢键
- 8.13 与蛋白质相关的项
- 8.14 与界面相关的项
本章将对分析模拟轨迹的各种不同方法进行讨论, 并给出相应的分析程序的名称. 与这些程序相关的输入输出的具体信息, 可以利用www.gromacs.org的在线手册进行查阅. 输出文件通常都是Grace/Xmgr的图形格式.
首先, 在8.1节对分析中使用的组的概念进行解释. 8.1.2节将解释一个新的概念–动态选择–只有一些分析工具支持这一概念. 然后, 将对不同的分析工具进行讲解.
8.1 使用组
gmx make_ndx, gmx mk_angndx, gmx select
在第三章, 我们解释了如何在mdrun中使用 原子组 (参看3.3节). 对大多数分析程序, 你也必须选择原子组. 虽然大多数程序都能产生一些默认的索引组, 但这些程序总是可以从索引文件中读入组. 让我们考虑一个具体的例子, A和B双组分混合物的模拟. 当我们需要计算A对B的径向分布函数(RDF, Radial Distribution Function) \(g_{AB}(r)\) 时, 我们必须计算
\[4\pi r^2 g_{AB}(r) = V \sum_{i \in A}^{N_A} \sum_{j \in B}^{N_B} P(r) \tag{8.1}\]
其中, \(V\) 为体积, \(P(r)\) 为距离A原子 \(r\) 处发现B原子的概率.
通过让用户在一个简单的文件中定义组A和B的 原子编号, 我们就能以最通用的方式计算 \(g_{AB}\), 而无须在RDF程序中对粒子类型做任何假定.
因此, 组可以包含一系列 原子编号, 但在一些情况下也可以包含 分子编号. 我们还可以利用 三联原子编号 指定一系列键角, 利用 四联原子编号 指定一系列二面角, 利用 原子编号对 指定一系列键或(分子中的)矢量
需要对分析程序指定索引文件的类型. 许多程序都可帮你创建这样的索引文件(index.ndx), 它们在创建时使用你输入的构型或拓扑信息. 要创建包含一系列 原子编号 (如 \(g_{AB}\) 例子中)的索引文件, 可以使用 gmx make_ndx或gmx select. 要创建键角或二面角的索引文件, 可以使用gmx mk_angndx. 当然, 你也可以手动创建这些索引文件. 索引文件的通用格式如下:
[ Oxygen ]
1 4 7
[ Hydrogen ]
2 3 5 6
8 9
可以看到, 组的名称写在方括号中. 随后的原子编号从1开始, 可以延续任意多行.
每个支持组的工具都会列出所有可选择的组, 供用户通过组的编号或名称进行选择. 实际上, 如果可以与其他的组区分开来, 使用组名称的头几个字母就足够了. 利用Unix shell可以在命令行中选择组名称, 而不是以通常的交互方式. 请查看www.gromacs.org给出的建议.
8.1.1 默认组
当没有为分析工具或grompp提供索引文件时, 会产生一些默认组以供选择:
System: 体系中所有的原子
Protein: 所有的蛋白质原子
Protein-H: 除氢原子外的所有蛋白质原子
C-alpha: \(\text C_\a\) 原子
Backbone: 蛋白质骨架原子, N, \(\text C_\a\) 和C
MainChain: 蛋白质主链上的原子: N, \(\text C_\a\), C和O, 包括C端的氧原子
MainChain+Cb: 蛋白质主链上的原子, 包含 \(\text C_\b\)
MainChain+H: 蛋白质主链上的原子, 包括骨架氨基氢原子和N端氢原子
SideChain: 蛋白质支链上的原子, 即除N, \(\text C_\a\), C, O, 骨架氨基氢原子, C端氧原子, N端氢原子以外的所有原子
SideChain-H: 除氢原子外的蛋白质支链上的原子
Prot_Masses: 除哑质量(创建NH3基团和色氨酸支链时使用的虚位点)外的蛋白质原子, 请参看5.2.2节. 只有当与Protein组不同时, 才包含此组
Non-Protein: 所有的非蛋白质原子
DNA: 所有的DNA原子
RNA: 所有的RNA原子
Water: 水分子(名称如SOL, WAT, HOH等). 参看residuetypes.dat文件中的完整列表
non-Water: 不属于Water组的任何粒子
Ion: 匹配residuetypes.dat文件中离子条目的任何名称
Water_and_Ions: Water和Ion组的组合
molecule_name: 所有不能被识别为蛋白质, DNA或RNA的残基/分子. 会为每个残基/分子创建一个组
Other: 不属于蛋白质, DNA, RNA的所有原子
不会创建空的组. 大部分组只包含蛋白质原子. 如果一个原子的残基名称存在于residuetypes.dat文件中, 并且被视为“蛋白质”, 这个原子就被视为蛋白质原子. 决定DNA原子, RNA原子等的方法类似. 如果需要修改这些分类, 你可以从库文件目录复制一份文件到你的工作目录, 然后编辑这个副本.
8.1.2 选择
gmx select
目前, 一些分析工具支持一个扩展的概念 (动态)选择, 它与传统的索引组主要存在三个区别:
通过文本指定选择, 而不是从文件中读入固定的原子编号. 选择使用的语法类似于VMD. 文本可以交互地输入, 也可以过命令行提供, 或是使用文件.
选择并不局限于原子, 也可以是分析的对象, 如一组原子的质心位置. 一些工具可能并不支持那些非单个原子的选择, 例如, 当它们需要的信息, 如原子名称或类型之类, 只对单个原子可用时.
选择可以是动态的, 即, 对不同的轨迹帧选择不同的原子. 这样就可以只对体系满足一定的几何条件的那部分进行分析.
作为动态选择的一个简单例子, resname ABC and within 2 of resname DEF将选择残基名称为ABC, 且距残基DEF中任何一个原子都不超过2 nm的所有原子.
对支持动态选择的工具也可以使用传统的索引文件, 像以前的工具一样: 可以为工具指定一个.ndx文件, 通过组编号或组名称直接从索引文件中选择一个组. 索引组也可以作为更复杂选择的一部分使用.
作为开始, 你可以使用单个结构运行gmx select, 利用交互的提示试验不同的选择. 这个工具提供了一些输出选项, -on和-ofpdb可以分别将选择的原子写入索引文件和.pdb文件中. 这些选项不允许测试质心位置的选择, 但可以测试其他选择, 并检查结果.
如果想了解选择的详细语法和各个关键词, 对任何支持选择的工具你可以在交互提示下键入help, 或使用gmx help selections命令. 帮助被划分为不同的子主题, 每个子主题可以通过像help syntax / gmx help selections syntax 这样的命令查看. 一些单独的选择关键词还有其自己的扩展帮助, 可通过像help keywords within这样的命令进行查看.
目前的交互提示没有提供很多的编辑功能, 如果需要它们, 你可以在rlwrap下运行程序.
对那些不支持选择语法的工具, 你可以使用gmx select -on生成静态的索引组并传递给工具. 但是, 这种作法只能使用那些完全支持动态选择的工具所提供的灵活性中的一小部分(仅仅前面三项中的第一项).
为了利用这些选择的优点, 你也可以编写自己的分析工具, 具的例子请参看安装目录下share/gromacs/template中的template.cpp文件.

gmx view窗口8.2 查看你的轨迹
gmx view
在进行分析之前, 先查看一下你的轨迹通常很有帮助. GROMACS提供了一个简单的轨迹查看器gmx view. 这个查看器的优点是它不需要OpenGL的支持, 有些机器–如一些超级计算机–通常不支持OpenGL. 你也可以利用查看器生成EPS格式的轨迹(图 8.1). 如果你需要更快更花哨的查看器, 有一些程序可以读取GROMACS格式的轨迹, 请查看我们主页上更新的链接.
8.3 通用性质
gmx energy, gmx traj
如果需要分析部分或全部的 能量 和其他性质, 如 总压力, 压力张量, 密度, 盒子体积 和 盒子尺寸, 请使用 gmx energy程序. 可以从一系列能量列表中进行选择, 如势能, 动能或总能, 也可以从对能量单独贡献的部分中进行选择, 如Lennard-Jones或二面角能量.
质心速度定义为
\[\bi V_{com} = {1\over M} \sum_{i=1}^N m_i \bi V_i \tag{8.2}\]
其中 \(M=\sum_{i=1}^N m_i\) 为体系的总质量. 可以利用程序gmx traj -com -ov对质心进行监测. 然而我们建议模拟时在每一步都移除质心的速度(参看第三章)!
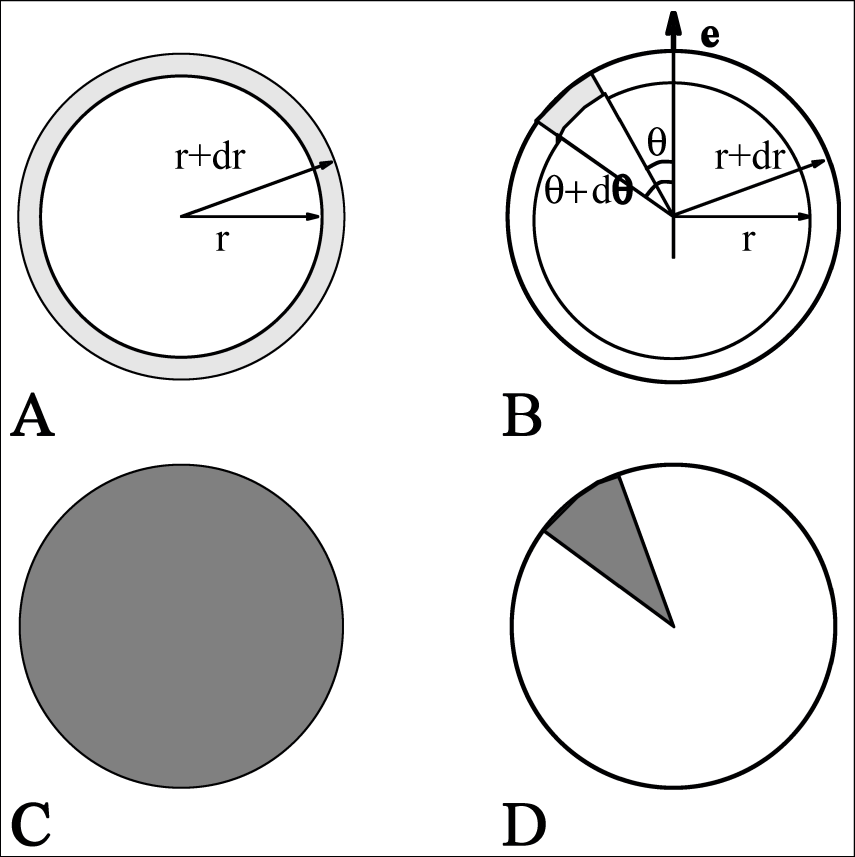
gmx rdf中切片的定义: A. \(g_{AB}(r)\). B. \(g_{AB}(r,\q)\). 切片为灰色, C. \(<\r_B>_{local}\) 的归一化. D. \(<\r_B>_{local,\q}\) 的归一化. 灰色为归一化体积.8.4 径向分布函数
gmx rdf
A类型粒子与B类型粒子之间的 径向分布函数 (RDF)或称对关联函数 \(g_{AB}(r)\) 的定义为
\[\alg g_{AB}(r) &= { <\r_B(r)> \over {<\r_B>}_{local} } \\ &= { 1\over {<\r_B>}_{local} } {1\over N_A} \sum_{i \in A}^{N_A} \sum_{j \in B}^{N_B} {\delta (r_{ij}-r) \over 4\pi r^2} \tag{8.3} \ealg\]
其中, \(<\r_B(r)>\) 为距离A粒子 \(r\) 处B粒子的密度, \(<\r_B(r)>_{local}\) 为所有以A离子为中心, 半径 \(r_{max}\) 的壳层内B离子的平均密度(图 8.2C)
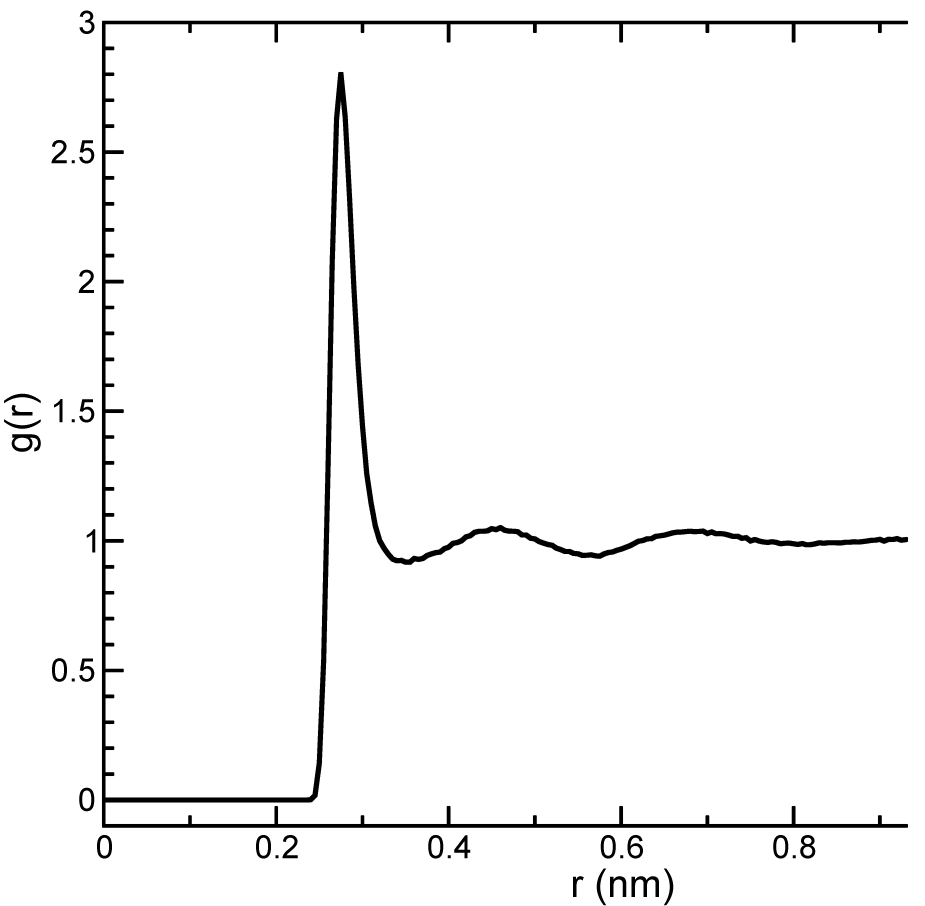
通常 \(r_{max}\) 的值取为盒子长度的一半. 计算时也会对时间进行平均. 具体计算时, 分析程序gmx rdf会将体系划分为球形切片(从 \(r\) 到 \(r+dr\), 图 8.2A), 并生成一个直方图而不是 \(\d\) 函数. SPC水模型氧-氧RDF[81]的一个例子如图 8.3.
也可以使用gmx rdf计算角度相关的RDF \(g_{AB}(r,\q)\), 其中角度 \(\q\) 根据特定的实验室坐标轴 \(\bi e\) 进行定义, 参看图8.2B.
\[\alg g_{AB}(r,\q) &= {1 \over {<\r_B>}_{local,\q} } {1 \over N_A} \sum_{i \in A}^{N_A} \sum_{j \in B}^{N_B} {\delta(r_{ij}-r)\delta(\theta_{ij}-\theta) \over 2\pi r^2 \sin(\theta)} \tag{8.4} \\ \cos(\theta_{ij}) &= {\bi r_{ij} \cdot \bi e \over \|r_{ij}\| \|e\|} \tag{8.5} \ealg\]
\(g_{AB}(r,\q)\) 在分析各向异性体系时很有用. 注意 在这种情况下, 归一化因子 \(<\r_B>_{local,\q}\) 为一直到 \(r_{max}\) 的所有从 \(\q\) 到 $\q+d\q$的角度切片的平均密度, 因此与角度相关. 参看图 8.2D
8.5 相关函数
8.5.1 相关函数的理论
文献[106]对相关函数的理论作了很好的介绍. 我们在这里只介绍GROMACS代码中对相关函数实现的各种细节. 性质 \(f(t)\) 的自相关函数(ACF) \(C_f(t)\) 的定义为
\[C_f(t) = {< f(\xi)f(\xi+t) >}_\xi \tag{8.6}\]
其中, 等号右边的记号表示对 \(\x\) 进行平均, 即对不同时间起点进行平均. 对两种性质 \(f(t)\) 和 \(g(t)\) 也可以计算交叉相关函数
\[C_{fg}(t) = {< f(\xi)g(\xi+t) >}_\xi \tag{8.7}\]
然而, 在GROMACS中不存在计算相关函数的标准方法( 注意: 你可以使用xmgr程序计算交叉相关). 相关函数对时间的积分为相关时间 \(\t_f\):
\[\tau_f = \int_0^\infty C_f(t) \rmd t \tag{8.8}\]
具体计算时, 相关函数是根据时间间隔为 \(\D t\) 的离散数据的计算的, 因此, MD模拟的ACF为
\[C_f(j \D t) = {1 \over N-j} \sum_{i=0}^{N-1-j} f(i\D t) f((i+j)\D t) \tag{8.9}\]
其中, \(N\) 为计算时所有可用的时间帧. 所得的ACF明显地只适用于具有相同时间间隔 \(\D t\) 的时间点. 对许多应用, 由于需要知道ACF短时间的行为(例如, 开始10 ps), 这常常意味着我们保存数据的时间间隔必须比感兴趣的时间尺度短得多. 方程8.9隐含的另一点是, 理论上我们不可能以相同精度计算所有时间点上的ACF, 因为对 \(C_f(\D t)\) 我们有 \(N-1\) 个点, 而对 \(C_f((N-1)\D t)\) 只有1个点. 然而, 如果我们只计算长度为 \(M \D t\) 的ACF, 其中 \(M\le N/2\), 我们可以同样的统计精度计算所有的点
\[C_f(j\D t) = {1 \over M} \sum_{i=0}^{N-1-M} f(i\D t) f((i+j)\D t) \tag{8.10}\]
当然, 这里的 \(j \le M\). \(M\) 有时被视为相关函数的时间延迟. 当决定这样做时, 对非常短的时间间隔(\(j \ll M\)), 我们故意不使用所有的点, 但这使得我们更容易解释结果. 当从模拟轨迹计算ACF的时候, 不能忽略的另一点是, 通常时间起点 \(\x\) (方程8.6)并不是统计无关的, 这可能使得结果存在偏离. 这可以利用块平均方法进行测试.
在这种方法中, 计算时只包含间距最少为时间延迟的时间起点, 例如, 使用 \(k\) 乘上间距为 \(M\D t\) 的起点(其中 \(kM \le N\)):
\[C_f(j\D t) = {1 \over k}\sum_{i=0}^{k-1} f(i M\D t) f((iM+j) \D t) \tag{8.11}\]
然而, 利用这种方式, 需要非常长的模拟才能得到高精确度的结果, 因为对ACF有贡献的点的个数少得多.
8.5.2 使用FFT计算SCF
根据方8.9计算ACF的代价正比于 \(N^2\), 计算量很可观. 然而, 通过使用快速Fourier变换计算卷积可以改进计算ACF的代价[106].
8.5.3 ACF的特殊形式
ACF存在一些重要的变形, 例如, 矢量 \(\bi p\) 的ACF
\[C_{\bi p}(t) = \int_0^\infty P_n(\cos \angle( \bi p(\xi), \bi p(\xi+t) ) \rmd \xi \tag{8.12}\]
其中 \(P_n(x)\) 为 \(n\) 阶Legendre多项式[1]. 这样的相关时间实际上可以NMR或其他弛豫实验中获得. GROMACS可以使用一阶和二阶Legendre多项式计算相关(方程8.12). 这种方法也可以用于旋转自相关(gmx rotacf)和偶极自相关(gmx dipoles).
为研究扭转角的动力学, 我们可以定义二面角的自相关函数[153]
\[C(t) = {<\cos(\theta(\tau)-\theta(\tau+t))>}_{\tau} \tag{8.13}\]
注意 这不是两个函数的乘积, 像通常的相关函数那样, 但可以将它重写成两个乘积加和的形式:
\[C_(t) = {<\cos(\theta(\tau)) \cos(\theta(\tau+t)) + \sin(\theta(\tau)) \sin(\theta(\tau+t))}_{\tau} \tag{8.14}\]
8.5.4 ACF的一些应用
gmx velacc程序计算 速度自相关函数
\[C_{\bi v}(\tau) = {<\bi v_i(\tau) \bi v_i(0)>}_{i \in A} \tag{8.15}\]
可以利用Green-Kubo关系计算自扩散系数[106]
\[D_A = {1 \over 3}\int_0^\infty {<\bi v_i(t) \cdot \bi v_i(0)>}_{i \in A} \rmd t \tag{8.16}\]
它是速度自相关函数的积分. 人们普遍相信, 速度自相关函数比均方位移收敛得更快(8.6节), 尽管均方位移也可用于计算扩散常数. 然而, Allen和Tildesley[106]警告我们, 不能忽略速度自相关函数的长时间贡献, 因此计算时必须当心.
另一个重要的物理量是偶极相关时间. A类型粒子的 偶极相关函数 可利用gmx dipoles计算, 其公式为
\[C_\mu(\tau) = {<\mu_i(\tau) \mu_i(0)>}_{i \in A} \tag{8.17}\]
其中 \(\m_i=\sum_{j \in i} \bi r_j q_j\). 偶极相关时间可以使用方程8.8 计算. 对此的应用请参看[154].
液体的粘度与压力张量 \(\bi P\) 的相关时间有关联. gmx energy可以计算粘度, 但计算结果并不是很精确[137], 实际上计算值并没有收敛.
8.6 均方位移
gmx msd
为决定A类型粒子的自扩散系数 \(D_A\), 可以使用Einstein关系式[106]:
\[\lim_{t \to \infty} { <\| \bi r_i(t)-\bi r_i(0) \|^2>}_{i \in A} = 6 D_A t \tag{8.18}\]
可使用gmx msd程序计算 均方位移 和 \(D_A\). 计算时通常使用一个包含原子编号的索引文件, 计算的MSD对这些原子进行平均. 对含有多个原子的分子, \(\bi r_i\) 可取为分子的质心位置. 在这种情况下, 你需要使用包含分子编号的索引文件. 但结果几乎与原子平均的结果完全相同. gmx msd程序也可用于计算一维或二维的扩散, 这对研究界面间的水平扩散很有用.
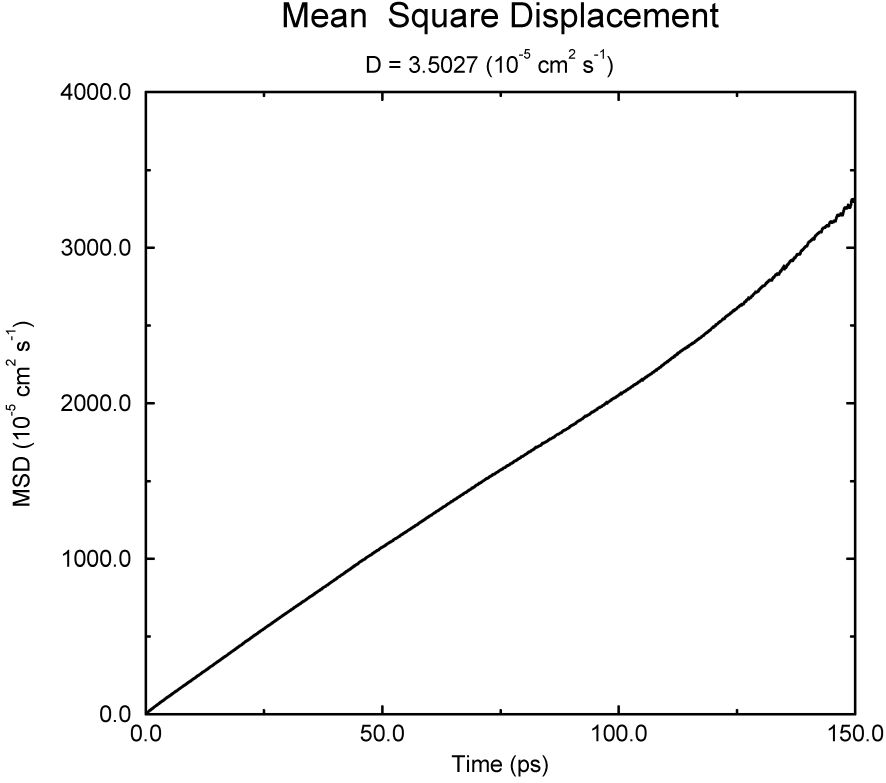
SPC水模型均方位移的一个例子如图8.4所示.
8.7 键/距离, 键角和二面角
gmx distance, gmx angle, gmx gangle
为监测分子中特定的 键, 或更一般的说法, 不同点之间的距离, 程序gmx distace可以计算距离随时间的变化以及距离的分布. 使用传统的索引文件时, 组里面应该包含一些原子编号对, 例如:
[ bonds_1 ]
1 2
3 4
9 10
[ bonds_2 ]
12 13
索引文件也支持选择, 第一行的两个位置定义了第一个距离, 第二个位置对定义了第二个距离, 以此类推. 你可以计算所有残基中CA和CB原子间的距离(假定每个残基或者含有这两类原子, 或者不含有任何一类), 选择的方法是:
name CA CB
选择也允许计算更广义的距离. 例如, 要计算两个残基质心之间的距离, 你可以使用
com of resname AAA plus com of resname BBB
gmx angle程序计算 键角 和 二面角 的时间分布, 还会给出平均键角或二面角. 计算时索引文件中需要包含三联或是四联原子编号:
[ angles ]
1 2 3
2 3 4
3 4 5
[ dihedrals ]
1 2 3 4
2 3 4 5
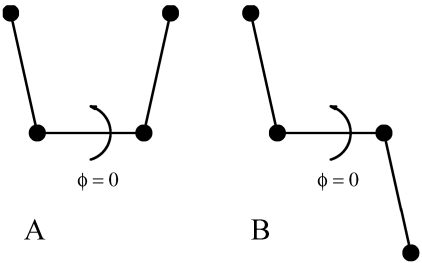
对二面角, 你可以使用 “生化约定”(\(\f=0\equiv cis\))或“聚合物决定”(\(\f=0\equiv trans\)), 参考图8.5.
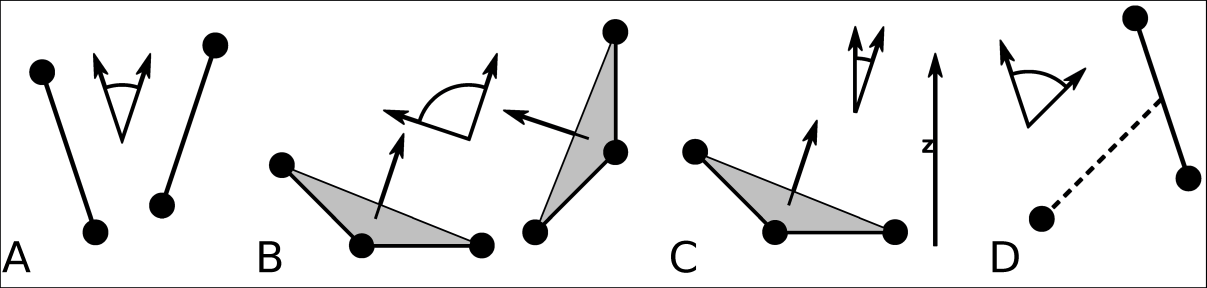
gmx gangle的角度选项: A. 两个矢量间的夹角. B. 两个平面间的夹角. C. 矢量和 \(z\) 轴间的夹角. D. 矢量和球的法向间的夹角. 也支持其他组合: 平面和矢量可以交换使用.gmx gangle程序计算角度时支持选择. 这个工具也可用于计算角和二面角, 但不能支持gmx angle的所有选项, 比如自相关或其他时间序列分析. 另外, 它支持两个矢量间的夹角, 矢量与平面, 两个平面(分别由2或3个点定义), 矢量/平面与 \(z\) 轴, 或矢量/平面与球的法向(由单一位置决定)间的夹角. 此外还支持矢量/平面相对于其第一帧位置的夹角. 对平面, gmx gangle使用的法向矢量垂直于平面. 参看图8.6 A, B, C中的定义.
8.8 回旋半径与距离
gmx gyrate, gmx distance, gmx mindist, gmx mdmat, gmx xpm2ps
作为结构密实度的粗略表征, 你可以利用gmx gyrate程序计算 回旋半径:
\[R_g = \left( {\sum_i \| \bi r_i\|^2 m_i \over \sum_i m_i} \right)^{1/2} \tag{8.19}\]
其中 \(m_i\) 为原子 \(i\) 的质量, \(\bi r_i\) 为原子 \(i\) 相对于分子质心的位置. 在表征聚合物溶液和蛋白质时, 回旋半径尤其有用.
有时描绘出两个原子间 距离 或是两个原子组(例如: 盐桥中的蛋白质支链)之间 最小 距离的图形很有趣, 一些组之间距离的计算可采用下面的方法:
两个组的 几何中心之间的距离 可以使用
gmx distance程序计算, 参看8.7节的论述.不同时刻两个原子组之间的 最小距离 可以使用
gmx mindist计算. 它同时也会计算这些组之间在一定半径 \(r_{max}\) 内的 接触数.为监测一个(蛋白质)分子中 氨基酸残基之间的最小距离, 你可以使用
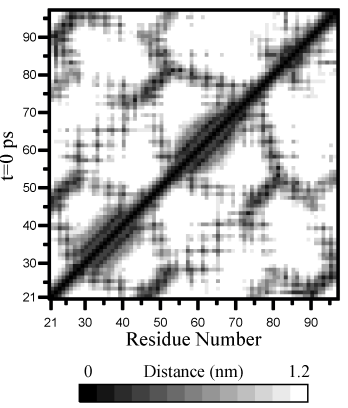
gmx mdmat程序. 两个残基 \(A_i\) 和 \(A_j\) 之间的最小距离的定义为任何一对原子(\(i \in A_i, j \in A_j\))之间的最小距离. 程序将输出一个所有残基之间最小距离的对称矩阵. 你可以使用xv等程序对此矩阵进行可视化. 如果想查看坐标轴和图例或者打印矩阵, 你可以使用xpm2ps将它转换为PS图片, 如图8.7.画出不同时刻的矩阵, 你就可以分析结构的变化和其他一些信息, 如盐桥的形成.
8.9 结构的根均方偏差
gmx rms, gmx rmsdist
一个分子中的某些原子相对于参考结构的 根均方偏差(RMSD) 可以利用gmx rms程序计算, 计算时先使用最小二乘方法
将结构拟合到参考结构(\(t_2=0\)), 再根据下式(方程8.20)计算 \(RMSD\)
\[RMSD(t_1,t_2) = \left[ {1\over M} \sum_{i=1}^N m_i \|\bi r_i(t_1)-\bi r_i(t_2)\|^2 \right]^{1/2} \tag{8.20}\]
其中 \(M=\sum_{i=1}^N m_i\), \(\bi r_i(t)\) 为原子 \(i\) 在 \(t\) 时刻的位置. 注意 计算 \(RMSD\) 时拟合并不需要使用相同的原子. 例如, 蛋白质通常利用骨架原子(N, \(\text C_\a\), C)进行拟合, 但 \(RMSD\) 可以基于骨架原子计算, 也可以基于整个蛋白质计算.
与把结构与 \(t=0\) 时刻的初始结构(例如一个晶体结构)进行比较不同, 你也可以使用 \(t_2=t_1-\t\) 时刻的结构计算方程 8.20. 其结果会给出迁移性与 \(\t\) 关系的洞察. 作为 \(t_1\) 和 \(t_2\) 函数的 \(RMSD\) 可以组成一个矩阵, 它给出了一条轨迹的漂亮的图形化解释. 如果轨迹中存在转变, 它们将在矩阵中清楚地显示出来.
作为替代, 也可以使用gmx rmsdist程序计算不拟合的 \(RMSD\)
\[RMSD(t) = \left[ {1\over N^2} \sum_{i=1}^N \sum_{j=1}^N \| \bi r_{ij}(t)-\bi r_{ij}(0)\|^2 \right]^{1/2} \tag{8.21}\]
其中, \(t\) 时刻原子间的距离 \(\bi r_{ij}\) 是与0时刻相同原子之间的距离相比
8.10 协方差分析
协方差分析也被称为主成分分析或主成分动力学[158], 利用它可以发现相关的运动. 它使用原子坐标的协方差矩阵 \(C\) 进行计算
\[C_{ij} = \left< M_{ii}^{1/2}(x_i-< x_i >) M_{jj}^{1/2}(x_j-< x_j >) \right> \tag{8.22}\]
其中 \(M\) 为包含原子质量的对角矩阵(质量加权分析)或单位矩阵(非质量加权分析). \(C\) 是对称的 \(3N \times 3N\) 矩阵, 可以利用正交变换矩阵 \(R\) 对其进行对角化
\[R^T C R = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_{3N}),\qquad \lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_{3N} \tag{8.23}\]
\(R\) 的列就是本征矢量, 也称为主模或基本模. \(R\) 定义了一个到新坐标系的变换. 将轨迹投影到主模上便得到主成分 \(p_i(t)\)
\[\bi p(t) = R^T M^{1/2}(\bi x(t)-<\bi x>) \tag{8.24}\]
本征值 \(\l_i\) 为主成分 \(i\) 的均方涨落, 头几个主模通常描述了体系聚集的整体运动. 可以利用一个(或多个)主模对轨迹进行过滤. 对一个主模 \(i\), 其方式如下
\[\bi x^f(t)=< \bi x > + M^{-1/2} R_{*i} p_i(t) \tag{8.25}\]
当对大分子进行分析时, 通常想要移除整体的转动和平动以便仅仅观察内部运动. 这可以通过最小二乘拟合到参考结构实现. 需要注意的是, 参考结构对系综需要具有代表性, 因为参考结构的选择会影响协方差矩阵.
始终都应该检查是否已经很好地定义了主模. 如果第一个主成分类似于半个余弦, 第二个主成分类似于整个余弦, 你可能正在过滤噪声(参见下文). 检查头几个主模相关的一个好方式是计算模拟前半部分和后半部分采样的重叠. 注意 这只适用于两部分使用相同的参考结构的情况.
文献[159]定义了一个很好的重叠度量. 协方差矩阵的元素正比于位移的平方, 因此需要取矩阵的平方根来检查取样的范围. 可以从本征值 \(\l_i\) 和本征矢量计算矩阵的平方根, 本征矢量对应于矩阵 \(R\) 的列. 对一个对称, 对角占优, 大小为 \(3N \times 3N\) 的矩阵 \(A\), 其平方根为
\[A^{1/2} = R \text{diag}(\lambda_1^{1/2}, \lambda_2^{1/2}, \dots, \lambda_{3N}^{1/2}) R^T \tag{8.26}\]
容易证明这个矩阵及其自身的乘积为矩阵 \(A\). 现在我们可以定义协方差矩阵 \(A\) 和 \(B\) 之间的差异 \(d\)
\[\alg d(A,B) &= \sqrt{\text{tr} \left( (A^{1/2}-B^{1/2})^2 \right)} \tag{8.27} \\ &= \sqrt{\text{tr} \left( A+B-2A^{1/2}B^{1/2} \right)} \tag{8.28} \\ &= \left( \sum_{i=1}^N (\lambda_i^A + \lambda_i^B) - 2 \sum_{i=1}^N \sum_{j=1}^N \sqrt{\lambda_i^A \lambda_j^B} (R_i^A \cdot R_j^B)^2 \right)^{1/2} \tag{8.29} \ealg\]
其中, \(\text{tr}\) 为矩阵的迹. 重叠 \(s\) 的定义为
\[s(A,B) = 1 - {d(A,B) \over \sqrt{\text{tr} A + \text{tr} B} } \tag{8.30}\]
当且仅当矩阵 \(A\) 和 \(B\) 全等时, 重叠为1. 当抽样的子空间完全正交时, 重叠为0.
一个常用的度量是协方差矩阵头几个本征矢量子空间的重叠. \(m\) 个正交矢量 \(\bi w_1, \cdots, \bi w_m\) 张成的子空间和 \(n\) 个正交矢量 \(\bi v_1, \cdots, \bi v_n\) 张成的参考子空间之间的重叠可定量为
\[\text{overlap}(\bi v, \bi w) = {1\over n}\sum_{i=1}^n \sum_{j=1}^m (\bi v_i \cdot \bi w_j)^2 \tag{8.31}\]
重叠会随着 \(m\) 的增加而增大, 当集合 \(\bi v\) 为集合 \(\bi w\) 的子空间时, 重叠为1. 这个方法的缺点在于没有考虑到本征值. 所有本征矢量的权重都相同, 当存在简并的子空间时(本质值相等), 计算的重叠太小.
另一个有用的检查是余弦含量. 已经证明随机扩散的主成分是余弦, 且其周期数等于主成分索引数的一半[160,159]. 本征值正比于索引数的–2次方. 余弦含量定义为
\[{2 \over T}\left( \int_0^T \cos\left({i\pi t \over T}\right) p_i(t) \rmd t \right)^2 \left( \int_0^T p_i^2(t) \rmd t \right)^{-1} \tag{8.32}\]
当头几个主成分的余弦含量接近1时, 最大的涨落与势能没有联系, 而是对应于随机扩散.
gmx covar可以构建并对角化协方差矩阵. 可以利用gmx anaeig对主成分和重叠(还有许多其他量)进行绘图和分析. 余弦含量可以利用gmx analyze计算.
8.11 二面角主成分分析
gmx angle, gmx covar, gmx anaeig
使用GROMACS可以在二面角空间[161]中进行主成分分析. 首先使用gmx mk_angndx或其他方法, 在索引文件中定义要计算的二面角, 然后使用gmx angle程序及其-or选项产生一个新的.trr文件, 其中包含了每个二面角分别在两个坐标系下的正弦和余弦值. 即, 在.trr文件中, 有相应于 \(\cos(\f_1)\), \(\sin(\f_1)\), \(\cos(\f_2)\), \(\sin(\f_2)\), \(\cdots\), \(\cos(\f_n)\), \(\sin(\f_n)\) 的一系列数字, 必要时, 会对数字序列补零. 然后, 你可以使用这个.trr文件作为gmx covar程序的输入, 像通常一样进行主成分分析. 为此, 你需要生成一个参考文件(.tpr,.gro,.pdb等), 其中包含与新的.trr文件相同数目的“原子”, 即, 对 \(n\) 个二面角, 你需要 \(2n/3\) 个原子(如果不是整数就舍去小数部分). 由于哑参考文件中的坐标与.trr文件中的信息毫无对应关系, 你需要使用gmx covar程序的-nofit选项. 对结果的分析可使用gmx anaeig.
8.12 氢键
gmx hbond
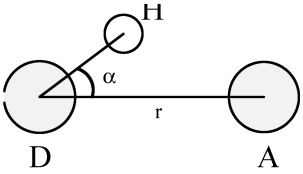
gmx hbond程序用于分析所有可能的施体D和受体A之间的 氢键 (HB). 分析时使用几何准则决定氢键的存在与否, 参看图 8.8:
\[\begin{split} r &\le r_{HB} = 0.35 \ \text{nm} \\ \alpha &\le \alpha_{HB} = 30^{\circ} \end{split} \tag{8.33}\]
参考值 \(r_{HB}=0.35 \text{nm}\) 对应于SPC水模型RDF的第一极小位置(参看图 8.3).
gmx hbond程序以下面的方式分析两组原子(它们必须相同或没有重叠)或指定的施体-氢-受体之间所有可能存在的氢键:
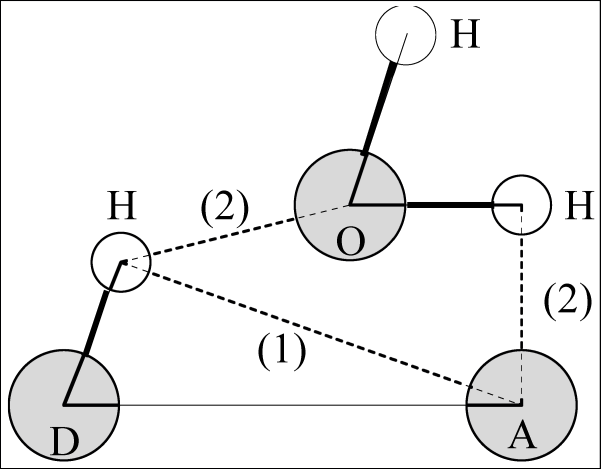
所有氢键中施体-受体距离的分布
所有氢键中氢-施体-受体之间夹角的分布
每个时间帧中氢键的总数目
残基之间实时的氢键数目, 划分到组 \(n-n+i\), 其中 \(n\) 和 \(n+i\) 代表残基编号, \(i\) 从0到6. \(i=6\) 的组也包括 \(i>6\) 的所有氢键. 这些组包括 \(n-n+3, n-n+4\) 和 \(n-n+5\) 氢键, 提供了 \(\a\) 螺旋, \(\b\) 转角或 \(\b\) 股形成的度量.
对所有氢键生存函数(0或1)的自相关函数进行平均, 可以计算氢键的寿命
\[C(\tau) = < s_i(t) s_i(t+\tau) > \tag{8.34}\]
对 \(t\) 时刻的氢键 \(i\), \(s_i(t)=\{0,1\}\). \(C(\t)\) 的积分给出了氢键平均寿命 \(\t_{HB}\) 的粗略估计
\[\tau_{HB} = \int_0^\infty C(\tau) \rmd \tau \tag{8.35}\]
程序会输出积分和完整的自相关函数 \(C(\t)\), 以便能够进行更复杂的分析(例如使用多指数拟合)得到 \(\t\) 的更佳估计值. 参考文献[162]给出了一个更完整的分析, 一个更花哨的选项是氢键动力学的Luzar和Chandler分析[163, 164].
生成大小为 #HB×#frames 的氢键存在映射图. 顺序与索引文件中的完全相同(见下文), 但反过来, 这意味着索引文件中的最后一个三联原子编号相应于存在映射图的第一行.
输出包含分析组的索引组, 这些组中所有的施体-氢原子对和受体原子, 分析组之间氢键中的施体-氢-受体三联对, 所有插入的溶剂分子.
8.13 与蛋白质相关的项
gmx do_dssp, gmx rama, gmx wheel
为分析蛋白质结构的变化, 你可以计算回旋半径或随时间变化的最小残基距离(参看8.8节), 或计算RMSD(参看8.9节).
在运行中你也可以观察 二级结构元素 的变化, 为此, 你可以使用gmx do_dssp程序, 它是商业程序DSSP[165]的接口界面. 更多的信息请参看DSSP的手册. 图 8.10 给出了一个典型的gmx do_dssp输出图.

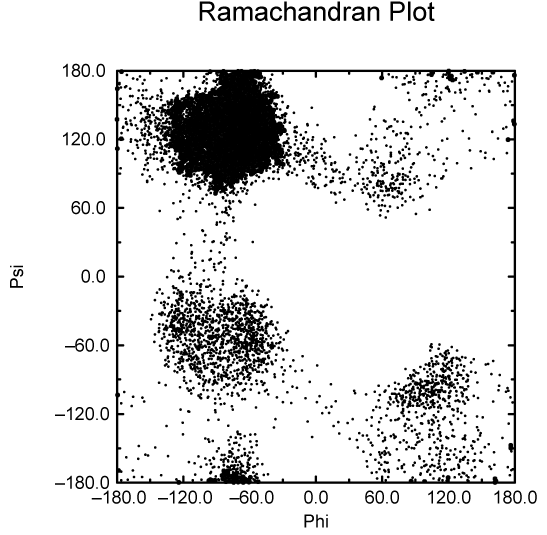
另一个重要的蛋白质分析是所谓的 Ramachandran图, 它是结构在蛋白质骨架的两个二面角 \(\f\) 和 \(\y\) 形成的平面上的投影. 参看图8.11.
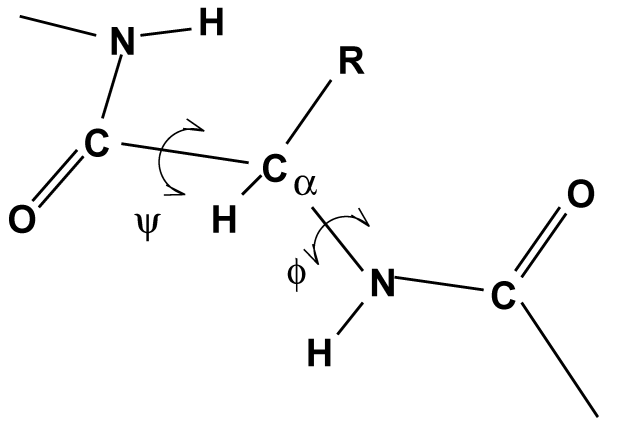
你可以使用gmx rama获得Ramachandran图. 图 8.12是一个典型的输出.
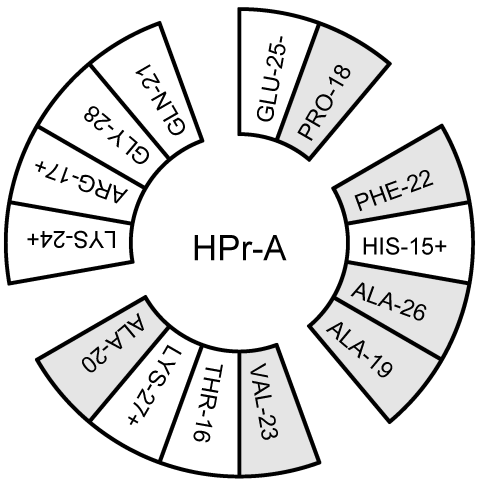
当研究 \(\a\) 螺旋时, 多肽的 旋轮投影 很有用, 它可用于查看一个多肽是否是两性的. 你可以使用gmx wheel程序获得这样的投影图. 图 8.13给出了两个例子.
8.14 与界面相关的项
gmx order, gmx density, gmx potential, gmx traj
当模拟具有长碳尾的分子时, 可以计算它们的平均取向. 有许多不同的序参数, 它们大多数是相关的. gmx order程序可利用下面的方程计算序参数
\[S_z = {3 \over 2} <\cos^2 \theta_z> -{1 \over 2} \tag{8.36}\]
其中 \(\q_z\) 为模拟盒子的 \(z\) 轴与待研究的分子轴之间的夹角. 后者被定义为从 \(\text C_{n-1}\) 到 \(\text C_{n+1}\) 的矢量. 可以同样的方式定义参数 \(S_x\) 和 \(S_y\). 尖括号隐含着要对时间和分子进行平均. 序参数可以在1(沿界面法向完全有序)和–1/2(完全垂直于界面法向)之间变化, 值为零时代表取向具有各向同性.
程序可以完成两件事. 它可以分别计算每个 \(\ce{CH2}\) 片段的序参数, 对所有三个轴的序参数, 或将盒子划分为切片并计算一个切片内每个片段序参数的平均值.
第一个方法给出了分子从头到尾如何排列的说明, 第二个方法给出了排列和盒子长度的关系.
从一条轨迹中可以计算出穿过界面的静电势(\(\y\)), 通过电荷密度(\(\r(z)\))的双重积分
\[\psi(z)-\psi(-\infty) = - \int_{-\infty}^z \rmd z' \int_{-\infty}^{z'} \r(z'') \rmd z''/\e_0 \tag{8.37}\]
其中, 位置 \(z =-\infty\) 在体相中足够远以致场强为零. 使用这种方法, 可以将总的势能“划分”为层和水分子的独立贡献. gmx potential程序将盒子划分为切片, 并对每个切片中原子的所有电荷进行加和. 然后程序会积分电荷密度得到电场, 对电场进行积分给出势能. 电荷密度, 电场和势能会写入xvgr输入文件中.
gmx traj是一个非常简单的分析程序, 它所做的是打印选中原子的坐标, 速度, 或力. 它也可以计算一个或多个分子的质心, 并将质心坐标打印到三个文件中. 这个分析程序本身可能并不是很有用, 但获得了选择的分子或原子的坐标后很利于进行进一步的分析, 不仅仅对于界面体系是这样.
gmx density程序计算组的质量密度, 并给出沿盒子轴向的密度分布. 对于观察组的分布或穿过界面的原子, 这很有用.
-
\(P_0(x)=1, P_1(x)=x, P_2(x)=(3x^2-1)/2\) ↩
