长度
质量
时间
能量
力
压强
浓度
密度
VDW参数
- 支持js函数:
**powsqrtexplog;absceilfloor;minmaxroundrandom;sincostan;asinacosatanatan2 -
支持常量符号:
pi;c:真空光速;Na:阿伏加德罗常数;qe:基元电荷;ang:埃;nmnm: 纳米;h:普朗克常数;hbar:h/2pi;amu:原子质量单位;ha:原子能量单位;bohr:原子长度单位;kb:玻尔兹曼常数;mu0:介磁常数;eps0:介电常数;me:电子质量;mp:质子质量;g:标准重力加速度;G:万有引力常数;atm:标准大气压;Po:标准压力;To:标准温度;R:摩尔气体常数;c2J:卡焦互换;j2c:焦卡互换;debye:偶极矩单位德拜
|
千克(kg) 克(g) 毫克(mg) 微克(μg) |
|
原子质量(amu/Dalton) 电子质量(me) 质子质量(mp) |
|
电子伏(eV) 兆电子伏(MeV) 吉电子伏(GeV) 太电子伏(TeV) |
|
吨(ton) 磅(pound) 克拉(carat宝石) 盎司(ounce) |
|
秒(s) 分(min) 时(h) 日(d) |
|
毫秒(ms) 微秒(μs) 纳秒(ns) 皮秒(ps) 飞秒(fs) 阿秒(as) 原子时间单位(au) |
|
月(m, 30 d) 年(a, 365 d) 平均月(29.53 d) 平均年(365.2422 d) |
|
焦耳(J) 卡(cal) 尔格(erg) |
|
千焦/摩尔(kJ/mol) 千卡/摩尔(kcal/mol) 兆焦/摩尔(MJ/mol) 兆卡/摩尔(Mcal/mol) |
|
哈垂(Hartree) 里德伯(Rydberg) |
|
静电势能(e2/Bohr) 静电势能(e2/nm) 静电势能(e2/Å) |
|
MD常用单位(amu-Å2/fs2) MD常用单位(amu-nm2/ps2) |
|
热力学温度(K) |
|
质量(kg) 原子质量(amu) |
|
电子伏(eV) 兆电子伏(MeV) 吉电子伏(GeV) 太电子伏(TeV) 拍电子伏(PeV) |
|
米(m) 厘米(cm) 毫米(mm) 微米(μm) 纳米(nm) 埃(Å) |
|
波数(m-1) 厘米波数(cm-1) |
|
赫兹(Hz) 兆赫兹(MHz) 吉赫兹(GHz) 太赫兹(THz) 拍赫兹(PHz) |
|
周期 秒(s) 周期 毫秒(ms) 周期 微秒(μs) 周期 纳秒(ns) 周期 皮秒(ps) 周期 飞秒(fs) 周期 阿秒(as) |
|
牛顿(N) 达因(dyn) 毫牛(mN) 微牛(μN) 纳牛(nN) 皮牛(pN) |
|
原子单位(Hartree/Bohr) 原子埃单位(Hartree/Å) |
|
静电埃(e2/Å2) 静电纳米(e2/nm2) |
|
MOPAC单位(kcal/mol-Å) MD常见单位(kJ/mol-Å) GROMACS单位(kJ/mol-nm) MD常用单位(amu-Å/fs2) MD常用单位(amu-nm/ps2) |
|
压强面积单位(Pa-m2) 压强面积单位(MPa-Å2) 压强面积单位(MPa-nm2) 压强面积单位(GPa-Å2) 压强面积单位(GPa-nm2) |
|
帕斯卡(Pa) 千帕(kPa) 兆帕(Mpa) 吉帕(Gpa) 达因/厘米2(dyn/cm2) |
|
巴(bar, 标准压力) 标准大气压(atm) |
|
毫米水柱(mmH2O) 毫米汞柱(mmHg) 托(Torr) |
|
M(mol/L) mM(mmol/L) μM(μmol/L) |
|
molec/cm3 molec/nm3 molec/Å3 |
|
使用温度/压强计算(理想气体) |
|
温度(K)
固定 压强(Pa) 固定 |
|
g/mL(g/cm3, kg/L) g/L(kg/m3) amu/Å3 |
|
使用分子量/摩尔浓度计算(纯物质) |
|
分子量(amu, g/mol)
固定 摩尔浓度(M, mol/L) 固定 |
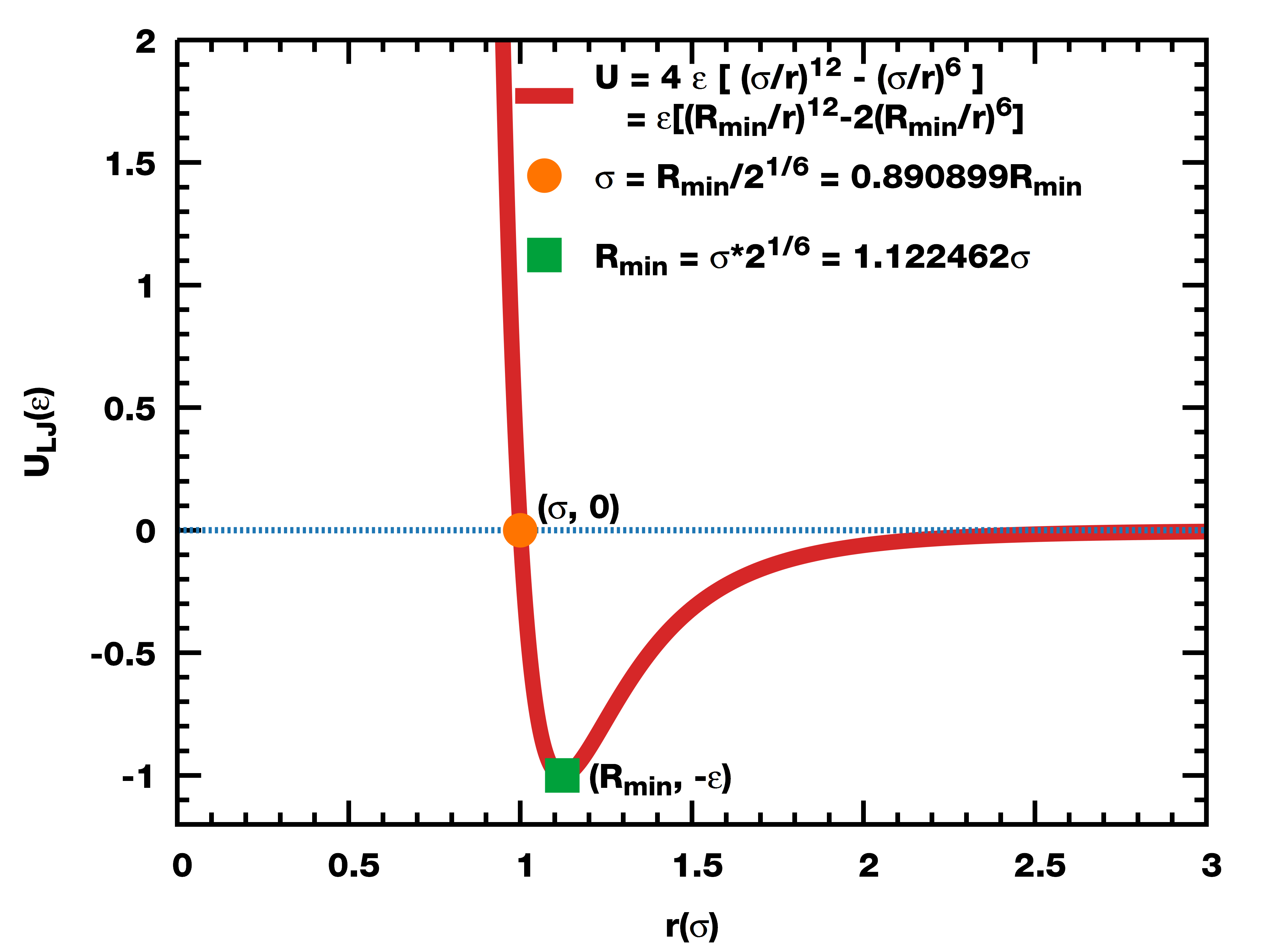 $U_{LJ}(r) = {C_{12} \over r^{12}} - {C_6 \over r^6} ={A \over r^{12}} - {C \over r^6} =4ε\left[\left( {σ\over r}\right)^{12}-\left({σ\over r}\right)^6\right] \\ =ε\left[\left( {R_{min}\over r}\right)^{12}-2\left({R_{min}\over r}\right)^6\right] =ε\left[\left( {R_e\over r}\right)^{12}-2\left({R_e\over r}\right)^6\right] =D_0\left[\left( {R_0\over r}\right)^{12}-2\left({R_0\over r}\right)^6\right]$ |
||||
| 原子 1 |
|
σ=(C12/C6)1/6(硬球半径) ε=C62/(4*C12)(势阱深度) Rmin=21/6σ(平衡距离) C6=4εσ6 C12=4εσ12 |
|
原子 2 |
| LB组合规则 (Lorentz-Berthelot) AMBER CHARMM |
|
σ=(σ1+σ2)/2 (算术均值) ε=sqrt(ε1*ε2) (几何均值) Rmin=21/6σ C6=4εσ6 C12=4εσ12 |
||
| OPLS-AA组合规则 (几何平均值) C6/C12组合规则 (C系数几何平均值) |
|
σ=sqrt(σ1*σ2)=(C12/C6)1/6 (几何均值) ε=sqrt(ε1*ε2)=C62/(4*C12) (几何均值) Rmin=21/6σ C6=4εσ6=sqrt(C6(1)*C6(2)) C12=4εσ12=sqrt(C12(1)*C12(2)) |
||
| 算术平均规则 (算术平均值) |
|
σ=(σ1+σ2)/2 (算术均值) ε=(ε1+ε2)/2 (算术均值) Rmin=21/6σ C6=4εσ6 C12=4εσ12 |
||
| A数据集 | B数据集 |
|---|---|
数值换算因子 输出格式
数据个数: 数据维数:
| 数据点 | 加和 $$\text{SUM}=\Sum_{j=1}^{N_{dim} } a_{i,j}$$ | 平均值 $$\text{AVG}={\text{SUM} \over N_{dim} }$$ | 平方和 $\text{SSQ}=\Sum_{j=1}^{N_{dim} } a_{i,j}^2$ | 长度 $$\text{LEN}=\sqrt{\text{SSQ} }$$ | 方差 $$\text{VAR}=\s^2={\text{SSQ} \over N_{dim} }-\text{AVG}^2$$ | 总体标准偏差 $$\text{RMSD}=\s=\sqrt{\text{VAR} }$$ | 样本标准偏差 $$\text{RMSE}=s={\sqrt{N_{dim} } \over \sqrt{N_{dim}-1 } }\text{RMSD}$$ |
|---|---|---|---|---|---|---|---|
| A | |||||||
| B | |||||||
| A-B |
数据
包含常数项
第一列为Y
包含常数项
第一列为Y
| 拟合数据(第一行给出每列名称, 应与拟合方程一致) |
|
|
拟合方程 拟合参数 | |
|
最大迭代次数 初始阻尼因子 最大梯度值 步长百分比 |