2013-08-13 14:05:39
取整和截断相关的函数, 有着各种不同的名称, 不同的定义, 很容易让人迷惑. 它们之间根据具体情况还可以相互转换成不同的写法, 更增添了混乱. 下面整理Fortran和C中的相关函数.
| 函数 | Fortran | C | |
|---|---|---|---|
| 向下取整⌊x⌋ | floor | floor | |
| 向上取整⌈x⌉ | ceiling | ceil | |
| 截断取整[x] | int/aint | int | |
| 四舍五入 | nint/anint | round | |
| 模/取余 | mod(x,p)=x-int(x/p)*p | x%p | |
| modulo(x,p)=x-floor(x/p)*p | |||
| 绝对值 |x| | abs | abs | |
| 符号 | sign(x, y) | ||
此外, 数学上还会使用如下去整函数
$frac(x)={x}=x-\lfloor x \rfloor=mod(x,1)$
以上这些函数组合起来, 基本能满足各种需要了.
下面是各个函数的图像, 数值可参看附表
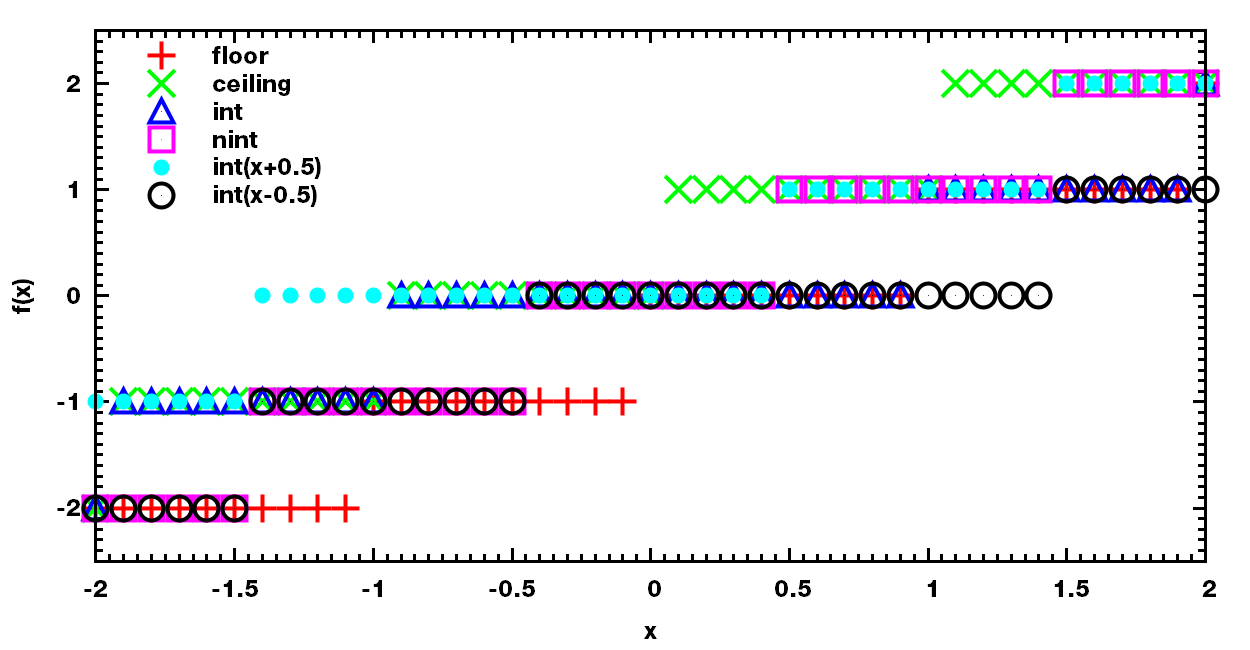
由图像与数值可知
\[int(x) = [x] = \begin{cases} \lfloor x \rfloor, & x>0 \\ \lceil x \rceil, & x<0 \end{cases}\] \[nint(x) = \begin{cases} int(x+1/2) = \lfloor x+1/2 \rfloor, & x>0 \\ int(x-1/2) = \lceil x-1/2 \rceil, & x<0 \end{cases}\]周期性边界条件PBC在使用时有两种情况, 设盒子长度为L, 粒子坐标为x
- 以左下角为坐标原点, 坐标 $x \in [0,L)$, 为使粒子处于盒内, 须 $x=x-\lfloor x \rfloor$
- 以中心为原点, 坐标 $x \in [-L/2,L/2)$, 常用于计算粒子之间距离, 此时又分两种情况
- x满足 $x \in [0,L)$, \(x = \begin{cases} x-L, &x>L/2 \\ x+L, &x<-L/2 \end{cases}\) 也可写为更紧凑形式: $x=x-sign(L,x), |x|>L/2$
- x未必满足 $x \in [0,L)$, 一般情况 \(x=x-nint({x \over L})L=\begin{cases} x-[x/L+1/2]L = x-\lfloor x/L+1/2 \rfloor L, &x>0 \\ x-[x/L-1/2]L = x-\lfloor x/L-1/2 \rfloor L, &x<0 \end{cases}\)
另外, 若想实现一定时间间隔 $\Delta t$ 取样, 本可利用 $mod(t, \Delta t)=t-\lfloor t/\Delta t \rfloor$ 实现. 但由于取整问题(前面说过), 遇到特定时间间隔时就会失效, 变通的方法是判断 $t$ 恰好能被 $\Delta t$ 整除, 即t的小数部分 ${t}$ 为零. 用 $t-nint(t/\Delta t)\Delta t$ 或 $mod(t+\Delta t/2, \Delta t)-\Delta t/2$ 可避免此问题.
参考
- http://en.wikipedia.org/wiki/Floor_and_ceiling_functions
- http://en.wikipedia.org/wiki/Periodic_boundary_conditions
| x | floor | ceiling | int | nint | int(x+0.5) | int(x-0.5) |
|---|---|---|---|---|---|---|
| -2.00 | -2 | -2 | -2 | -2 | -1 | -2 |
| -1.80 | -1 | -1 | ||||
| -1.50 | ||||||
| -1.20 | -1 | 0 | -1 | |||
| -1.00 | -1 | |||||
| -0.90 | 0 | 0 | ||||
| -0.80 | ||||||
| -0.70 | ||||||
| -0.60 | ||||||
| -0.50 | ||||||
| -0.40 | 0 | 0 | ||||
| -0.30 | ||||||
| -0.20 | ||||||
| -0.10 | ||||||
| 0.00 | 0 | |||||
| 0.10 | 1 | |||||
| 0.20 | ||||||
| 0.30 | ||||||
| 0.40 | ||||||
| 0.50 | 1 | 1 | ||||
| 0.60 | ||||||
| 0.70 | ||||||
| 0.80 | ||||||
| 0.90 | ||||||
| 1.00 | 1 | 1 | ||||
| 1.10 | 2 | |||||
| 1.20 | ||||||
| 1.50 | 2 | 2 | 1 | |||
| 1.80 | ||||||
| 2.00 | 2 | 2 |
