2013-08-16 13:53:46 初稿
2014-12-15 17:17:19 修正代码bug, 增加网络版工具
八面体和截角八面体构型在纳米金属团簇的结构中比较常见, 在展示或计算时我们都需要构建这些结构.
原理:正方体切除6顶点得正八面体, 正八面体切除6顶点得截角八面体
具体方法:长度以原子个数计, 以简单立方晶胞为例, 面心立方、体心立方晶胞同理
-
根据需要大小构建相应的超晶胞, 设其边长为Nedg
-
以 \(\{\pm N_{edg} \pm N_{edg} \pm N_{edg}\}\) 6个面依次切取超晶胞, 只保留面内的部分, 得正八面体团簇
-
以 \(X=\pm N_{top}, Y=\pm N_{top}, Z=\pm N_{top}\) 6个面上下左右前后依次截取所得正八面体, 得截角八面体, Ntop为切除四面体的边长
截角八面体有6个四边形面和8个六边形面, 设Nrec和Nhex分别为四边形边长和六边形边长, 它们与正方体边长和切除四面体边长的关系如下:
\[\begin{align} N_{hex} &=N_{edg}-2N_{top} \quad &N_{rec} &=N_{top}+1 \\ N_{top} &=N_{rec}-1 \quad &N_{edg} &=N_{hex}+2N_{top} \end{align}\]利用这些关系我们便可以得到任意边长的截角八面体了.
正八面体(边长7)

截角八面体(边长3)

截角八面体(面心立方, 边长3)
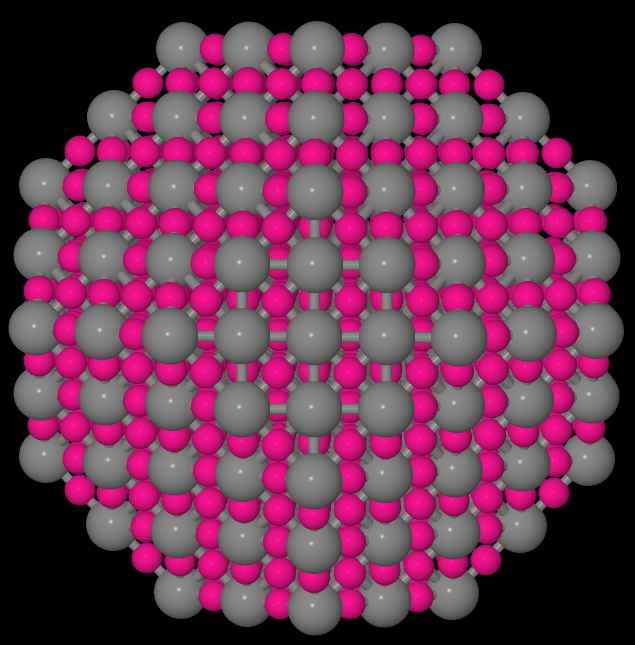
截角八面体(体心立方, 边长3)
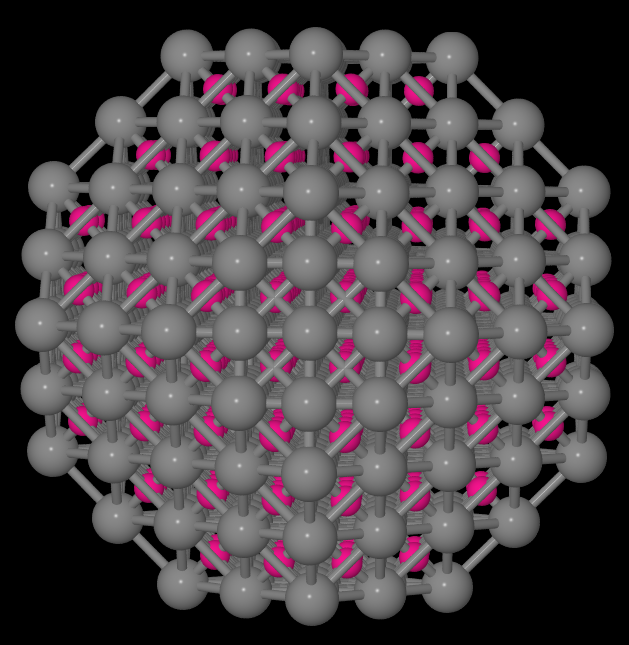
基于JavaScript的在线工具(2014-12-15更新)
虽然我发了这篇博文, 但还是经常有人向我询问怎么创建, 为了尽量避免浪费时间, 我现在将其做成一个在线小工具, 只要你选好参数, 就可以得到相应的团簇坐标. 建议使用谷歌的Chrome浏览器, 因为我没有在其他浏览器上进行测试.
如果你需要创建八面体或截角八面体团簇, 请移步这里. 若发现问题, 敬请告示.
代码
# Language: bash
################################################################################
# A script to generate Octahedron/Truncated Octahedron of SC/BCC/FCC
# Jicun LI Jerkwin@gmail.com
# 2013-08-17: Demo
# 2014-12-15: fix bug
################################################################################
awk '
BEGIN { YesBCC=0; YesFCC=0
Nrec=3; Nhex=3; YesCut=1 # Nhex=N-2*Ntop; Nrec=Ntop+1
Ntop=Nrec-1
Nedg=Nhex+2*Ntop
a=1; b=1; c=1; Reps=1-1/Nedg+1E-3
Ntot=0
for(i=-Nedg; i<=Nedg; i++) {
for(j=-Nedg; j<=Nedg; j++) {
for(k=-Nedg; k<=Nedg; k++) {
Ntot=Ntot+1
x=i*a; y=j*b; z=k*c
S[Ntot]="C"; X[Ntot]=x; Y[Ntot]=y; Z[Ntot]=z
if(YesBCC) {
Ntot=Ntot+1
S[Ntot]="BCC";
X[Ntot]=x+0.5*a; Y[Ntot]=y+0.5*b; Z[Ntot]=z+0.5*c
} else if(YesFCC) {
Ntot=Ntot+1
S[Ntot]="FCC";
X[Ntot]=x+0.5*a; Y[Ntot]=y+0.5*b; Z[Ntot]=z
Ntot=Ntot+1
S[Ntot]="FCC";
X[Ntot]=x+0.5*a; Y[Ntot]=y; Z[Ntot]=z+0.5*c
Ntot=Ntot+1
S[Ntot]="FCC";
X[Ntot]=x; Y[Ntot]=y+0.5*b; Z[Ntot]=z+0.5*c
}
}
}
}
Natm=0
Ncut=Nedg-Ntop-0.5001;
Na=Nedg; Nb=Nedg; Nc=Nedg;
Ra=1/(Na*a); Rb=1/(Nb*b); Rc=1/(Nc*c)
for(i=1; i<=Ntot; i++) {
x=X[i]; y=Y[i]; z=Z[i]
if( x*Ra+y*Rb+z*Rc<Reps && x*Ra-y*Rb+z*Rc<Reps \
&& -x*Ra+y*Rb+z*Rc<Reps && -x*Ra-y*Rb+z*Rc<Reps \
&& x*Ra+y*Rb-z*Rc<Reps && x*Ra-y*Rb-z*Rc<Reps \
&& -x*Ra+y*Rb-z*Rc<Reps && -x*Ra-y*Rb-z*Rc<Reps ) {
if(YesCut) {
if(-Ncut*a<x && x<Ncut*a && -Ncut*b<y && y<Ncut*b && -Ncut*c<z && z<Ncut*c) {
Natm=Natm+1; YesIn[i]=1
}
} else {
Natm=Natm+1; YesIn[i]=1
}
}
}
print Natm
print "BCC= " YesBCC, "FCC= " YesFCC, "Nhex= " Nhex, "Nrec= " Nrec
for(i=1; i<=Ntot; i++) {
if(YesIn[i]) printf "%5s %8.3f %8.3f %8.3f\n", S[i], X[i], Y[i], Z[i]
}
} '
参考
