2013-03-18 10:26:43
2014-07-12 17:52:11 补充
设空间维数为n, 则此空间中任意两个向量之间的夹角 $\theta$ 符从一定的分布, 其概率密度函数如下:
\[p(\theta)= \frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})} \frac{\sin^{n-2}(\theta)}{\sqrt\pi}\]对二维平面, $n=2, p(\theta)=\frac{1}{\pi}$
对三维空间, $n=3, p(\theta)=\frac{1}{2}\sin \theta$
对于我们熟悉的二维平面与三维空间, 证明很简单. 对于更高维的空间, 我们已经很难想象, 可借助于n维球体的表面积公式加以证明.
对n维球体, 设半径为R, 则其体积 $V_n=\frac{\pi^{n/2}}{\Gamma(n/2+1)}R^n$, 相应的n-1维球面的表面积
\[S_{n-1}={\rmd {V_n} \over \rmd R}={2\p^{n/2} \over \G(n/2)} R^{n-1}\]设第一个向量处于某一坐标轴上, 第二个向量与此坐标轴所成的角度为 $\theta$ , 则当此角度增加 $d\theta$ 时会在球面上切割出的一个带状区域, 此带状区域的面积 $\Delta S$ 与球总表面积 $S_{n-1}$ 的比值即为要求的概率密度. 即,
\[p(\theta)\rmd \theta={\Delta S \over S_{n-1} }={S_{n-2}(R\sin\theta)R \rmd \theta \over S_{n-1}(R)}\]下面是二至十维和二至一百维空间的 $p(\theta)$.
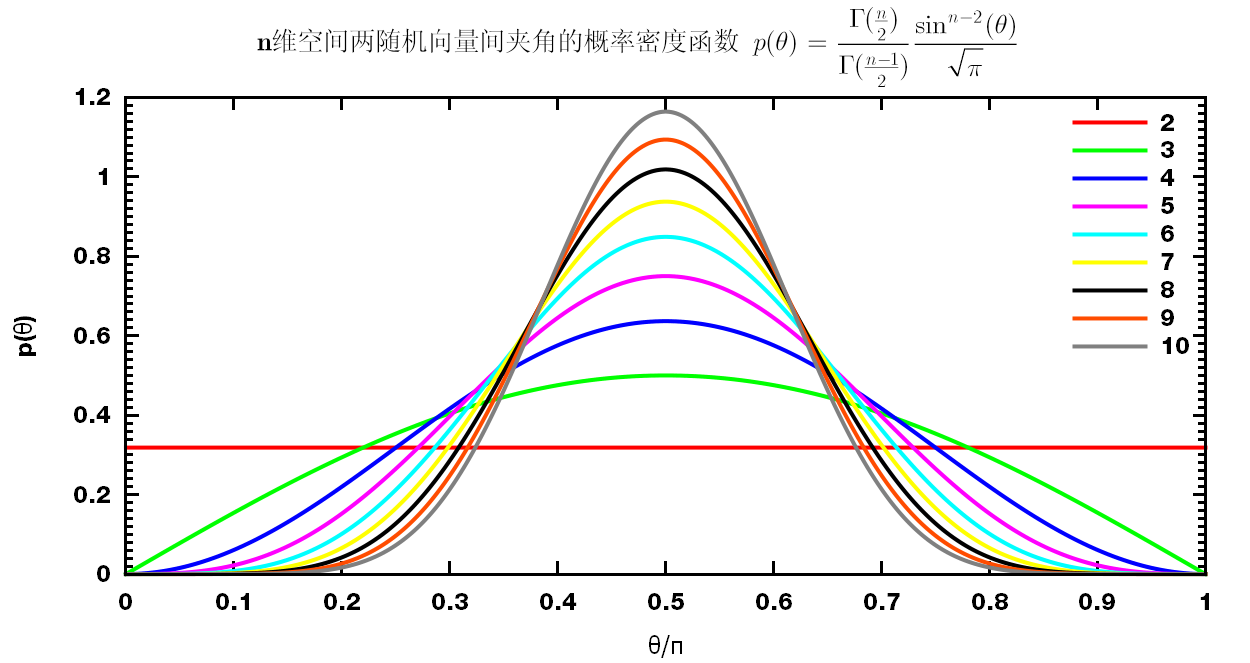
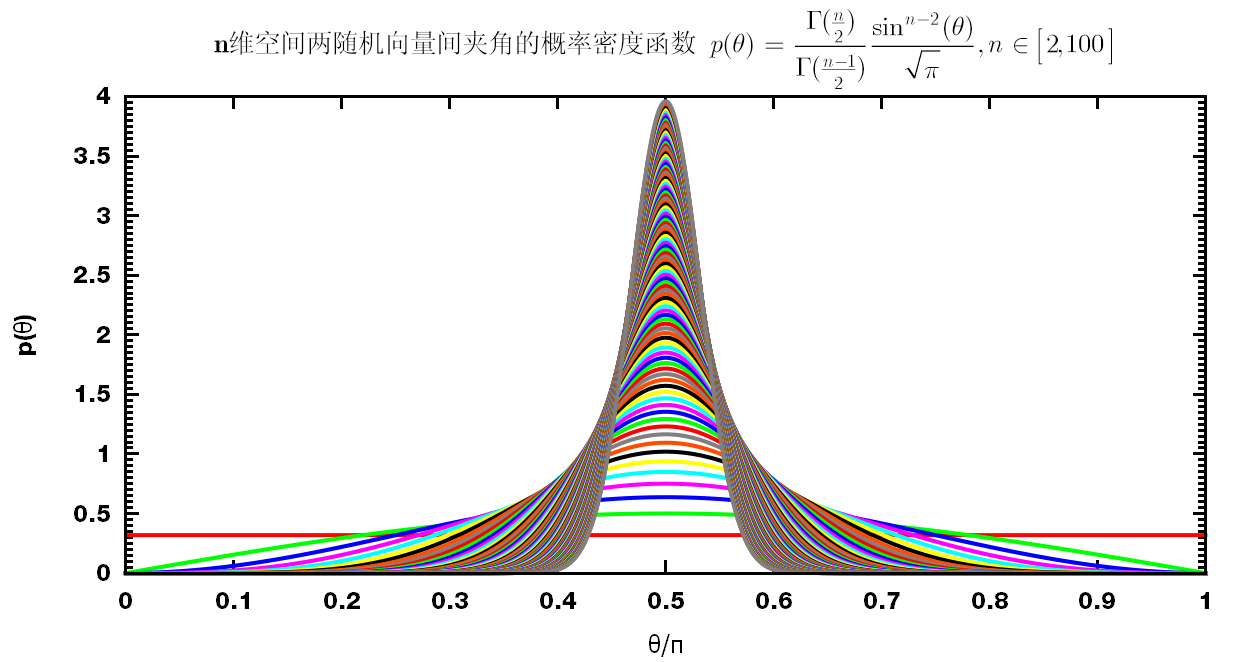
可以看出, 任意两向量正交(即互相垂直)的概率最大, 而且此概率随空间维数的增大而增大.
对我们熟悉的三维空间, $p(\theta)={1 \over 2}\sin \theta$ 稍有特殊: $\theta$ 满足此分布时, $\cos\theta$ 符从均匀分布. 说明如下.
若已知变量 $x$ 服从分布 $p(x)$, 变量 $y=y(x)$, 根据概率的基本变换定律, 即变换前后出现的概率不变,
\[\left\vert p(x) \rmd x \right\vert= \left\vert p(y) \rmd y\right\vert\]则变量 $y=y(x)$ 服从分布
\[p(y)=p(x) \left\vert {\rmd x \over \rmd y} \right\vert = p(x){1 \over \left\vert \rmd y/\rmd x \right\vert}\]由此, 可推知任意分布相应的均匀分布变换. 对分布 $p(x)={1 \over 2} \sin \q$, $y={1- \cos \q \over 2}$ 为[0,1]上的均匀分布, 恰好对应于 $\q$ 的范围 $[0,\p]$. 当讨论两向量夹角的分布时, 可以使用 $y$ 作图, 扣除 $\q$ 的非均匀分布带来的影响.
对 $\cos\theta$ 的任意函数 $f(\cos\theta)$, 其平均值
\[\alg \langle f(\cos\theta) \rangle &=\int_0^\pi f(\cos\theta)p(\theta)\rmd \theta \\ &={1 \over 2}\int_0^\pi f(\cos\theta)\sin\theta \rmd\theta \\ &={1 \over 2}\int_{-1}^1 f(\cos\theta)\rmd{\cos\theta} \\ &={1 \over 2}\int_{-1}^1 f(x)\rmd x \ealg\]这样
\[\langle \cos^m\theta \rangle=\begin{cases} 0 , &m=2k+1 \\ {1 \over m+1 }, &m=2k \end{cases}\]知道这一点, 在求与 $\cos(\theta)$ 有关的平均值时就简单了许多. 如半径为R的球面上任意两点之间距离 $r=\sqrt{2}R\sqrt{(1-\cos\theta)}$, 其平均值 $\langle r \rangle={4 \over 3}R$. 而 $\langle r^2 \rangle=R^2$.
参考
- 中文维基, n维球面
- 百度贴吧, n维空间中两个随机向量夹角的概率密度函数
