- 2013-04-18 10:43:35 发布图片
- 2013-11-14 21:18:18 增加教程
- 2016-09-07 20:17:18 颜色映射
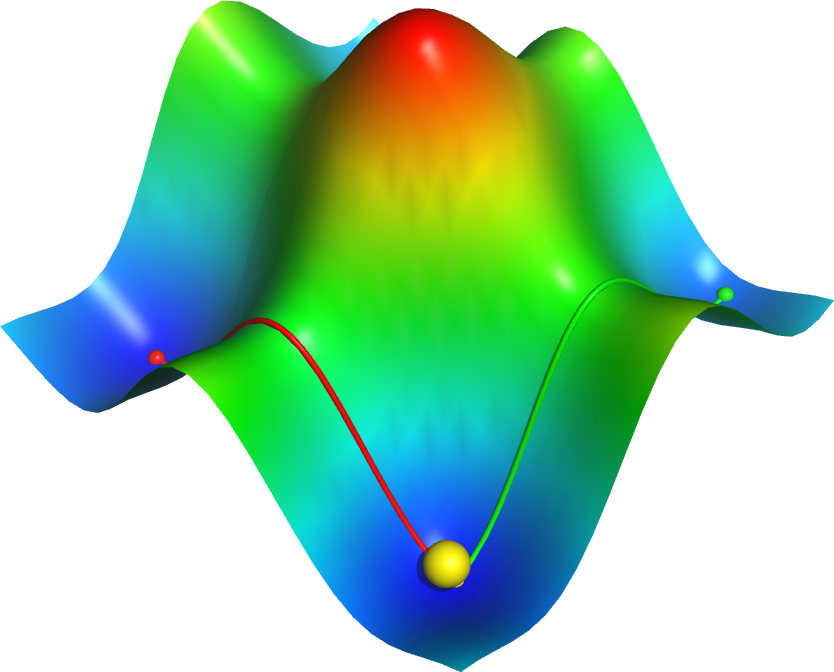
利用PyMOL内置的OpenGL制作了势能面反应的示意图, 具体制作过程容后再讲.
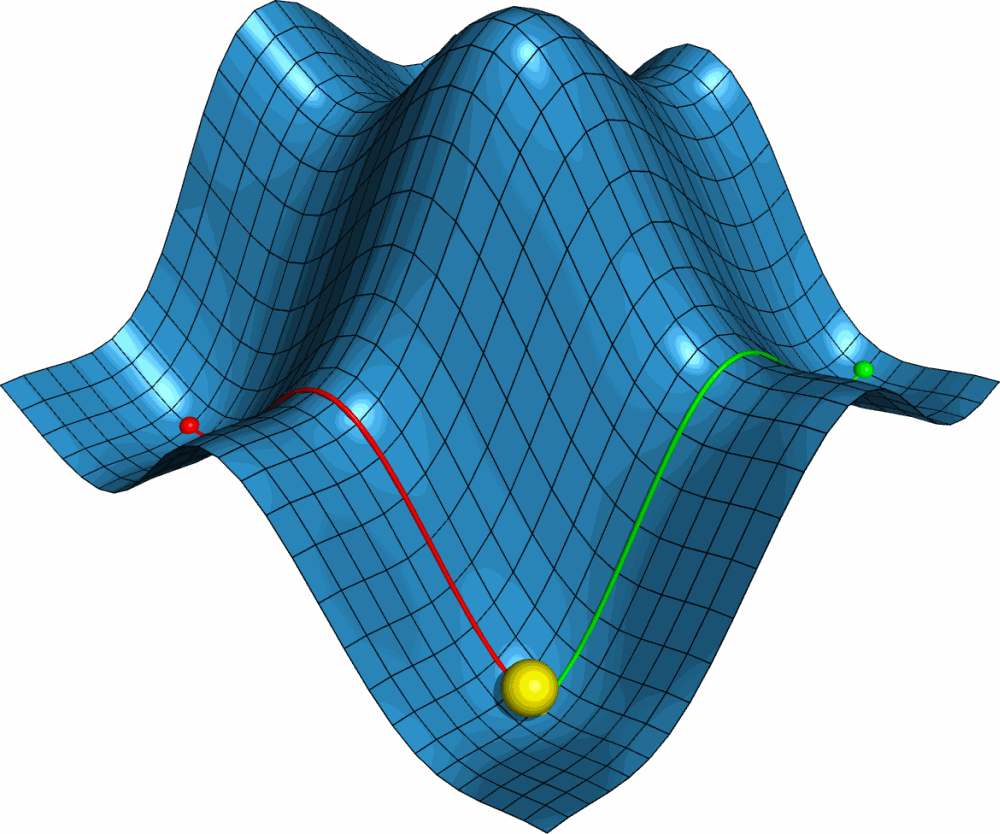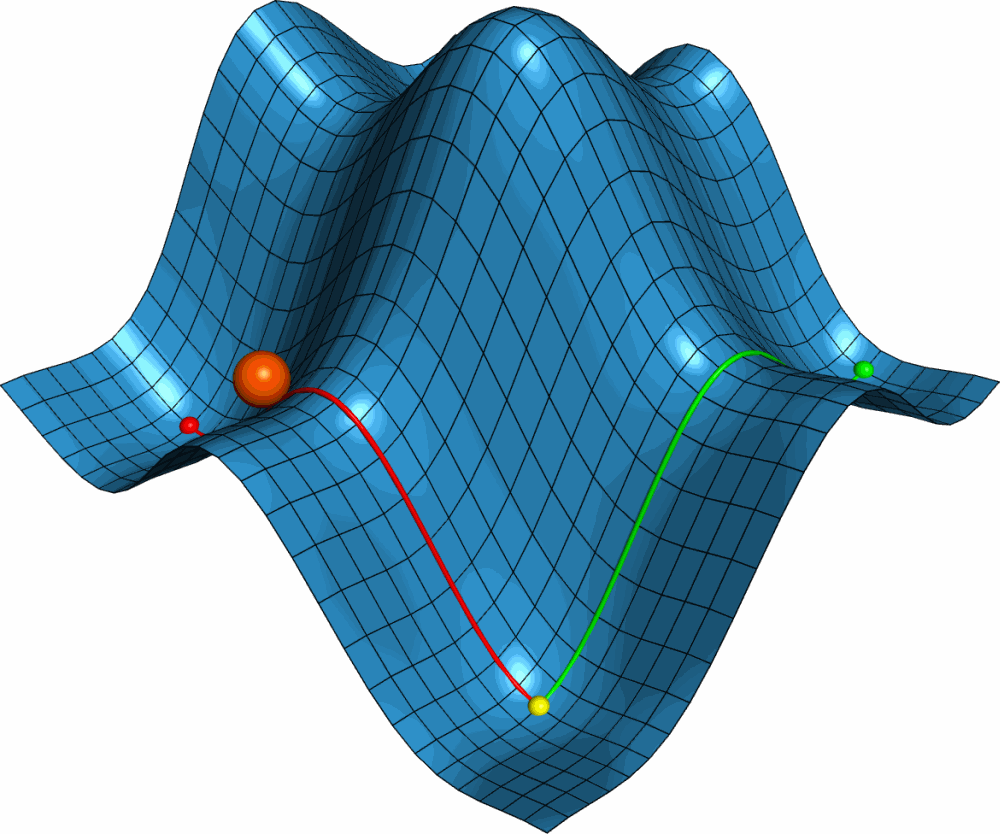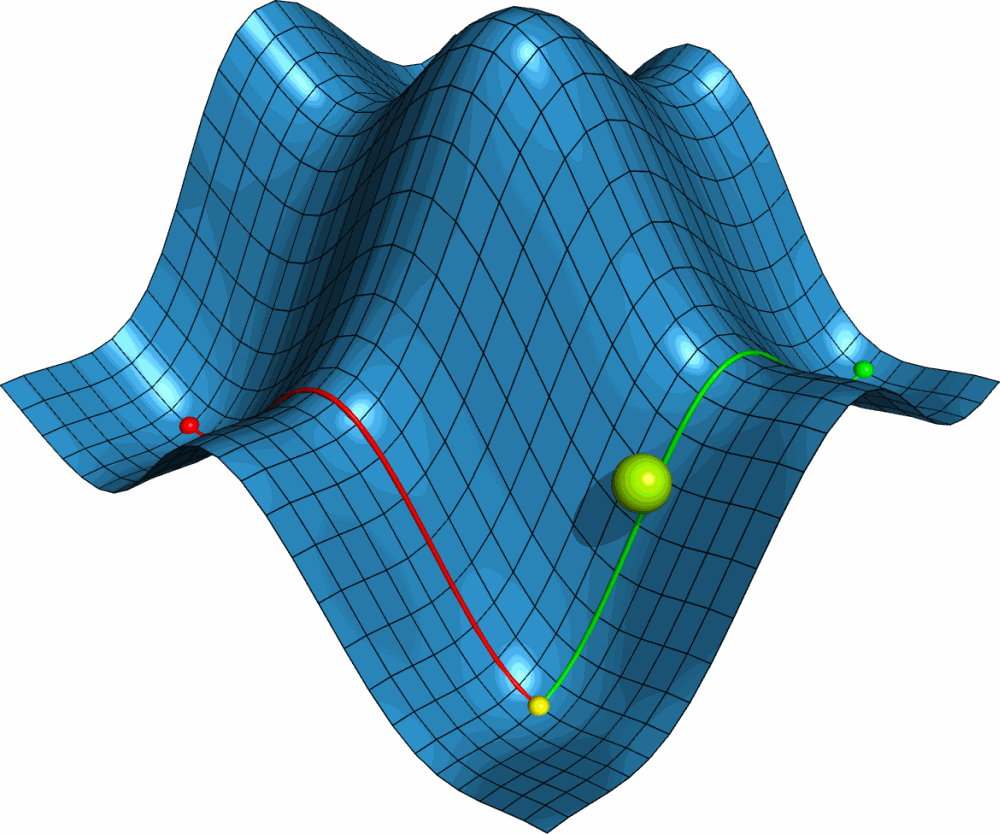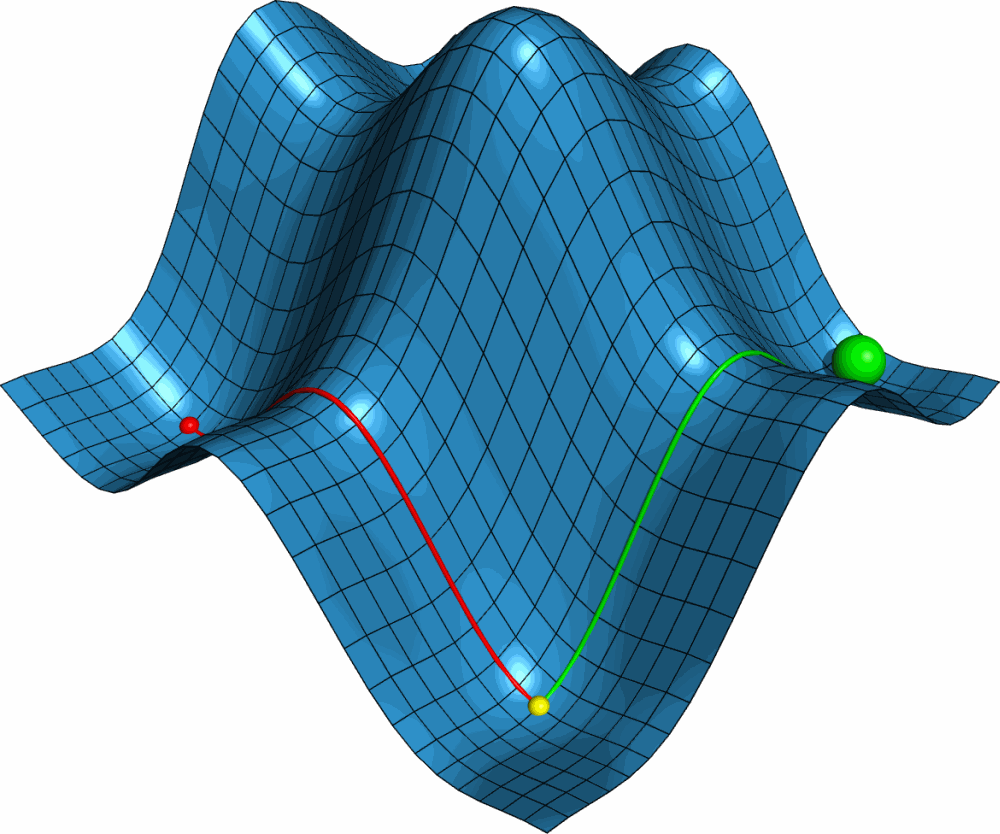
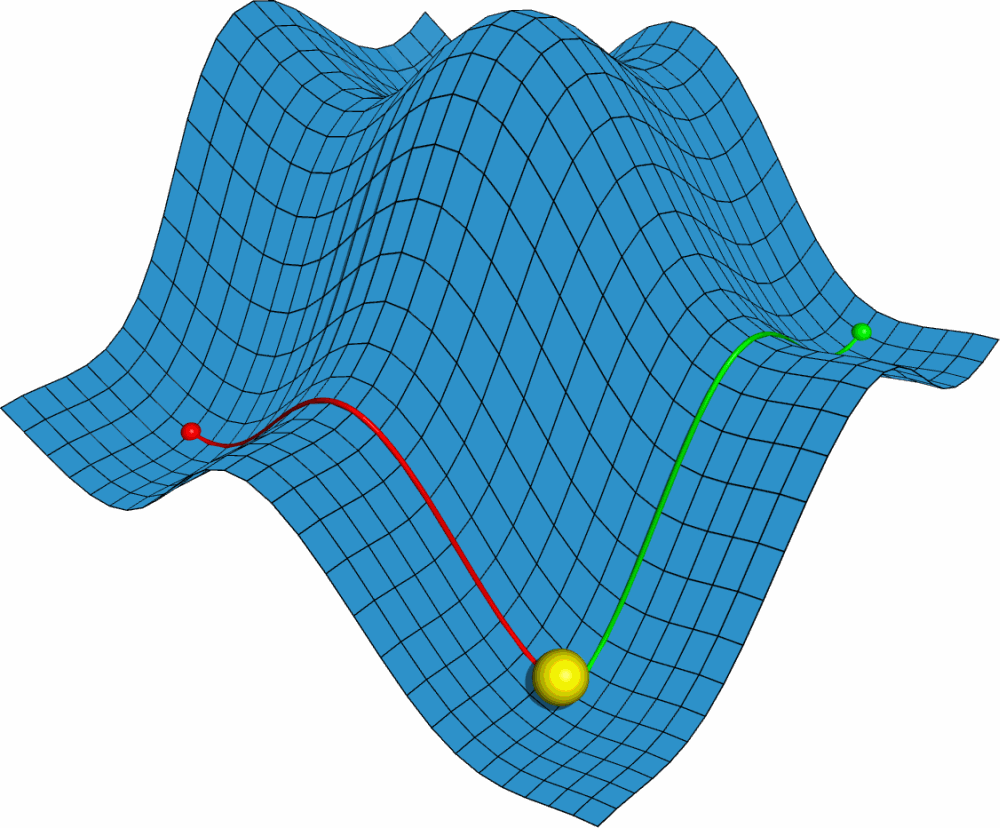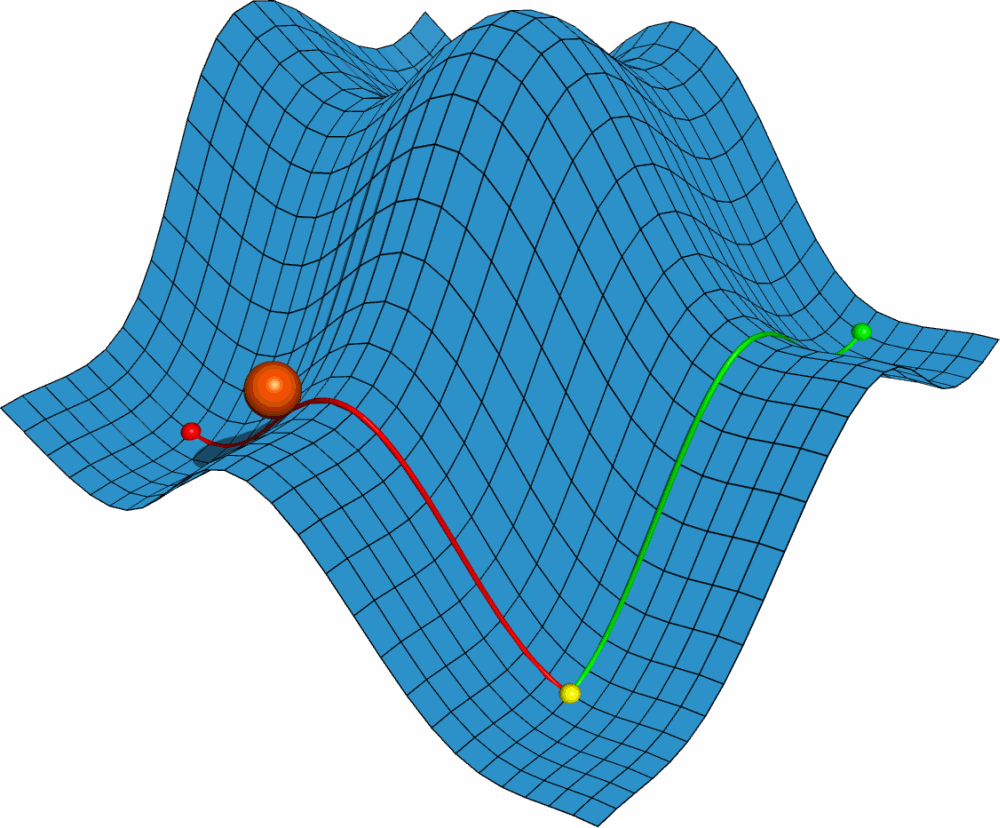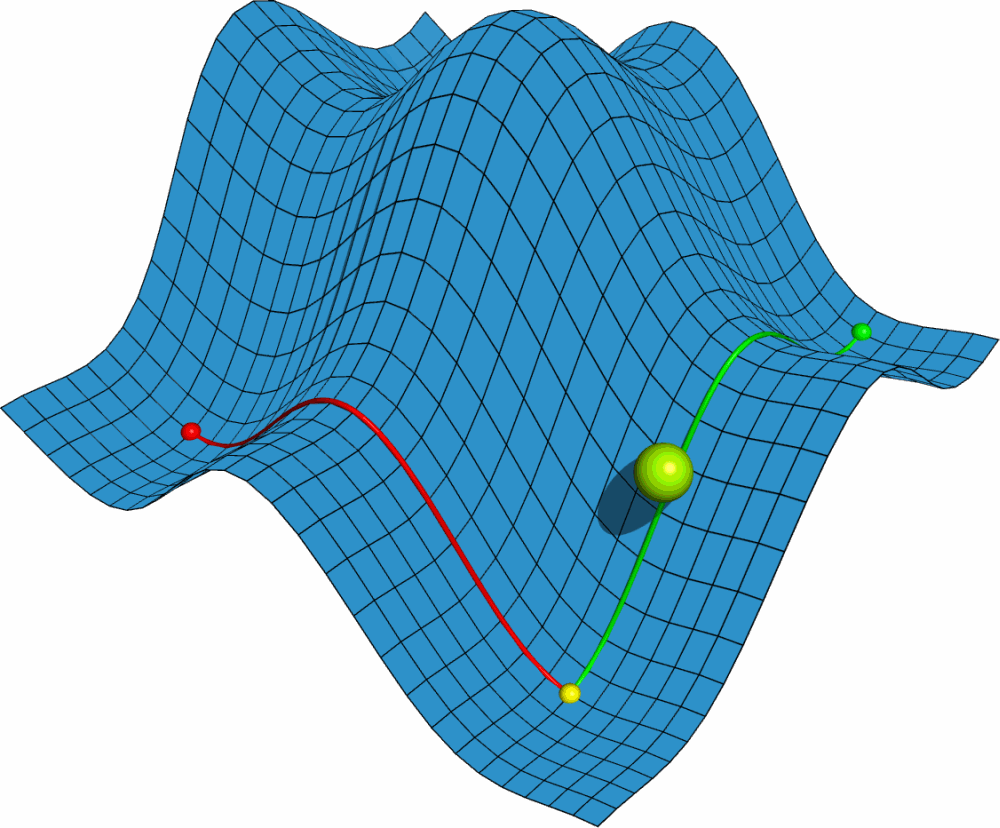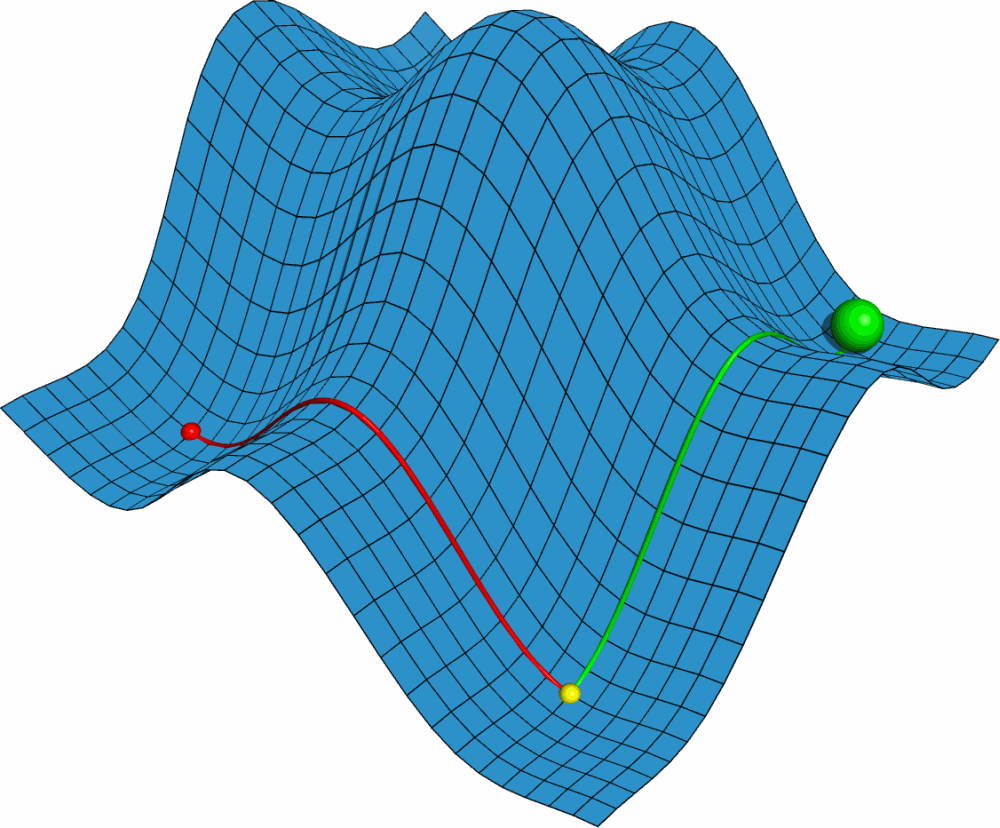
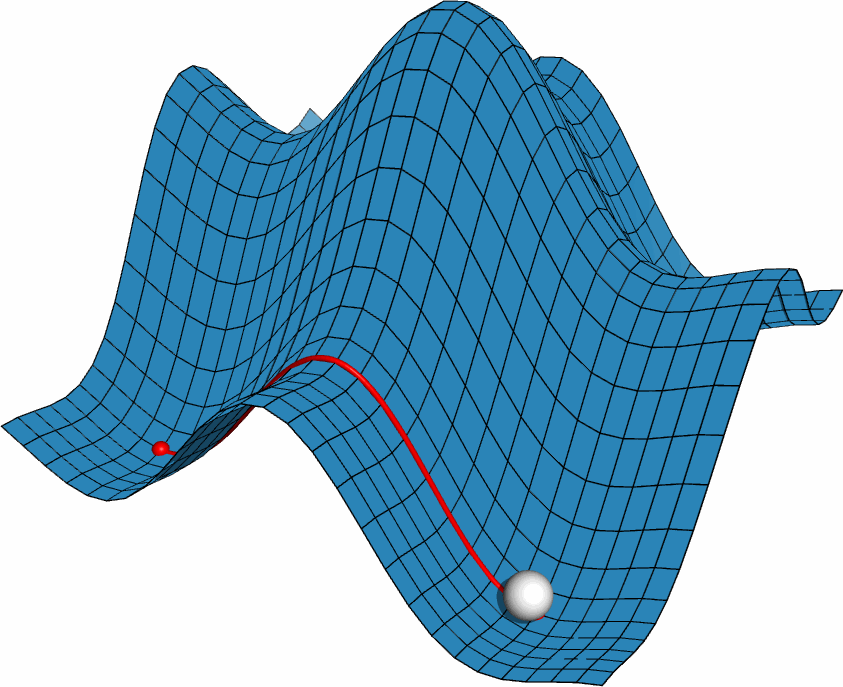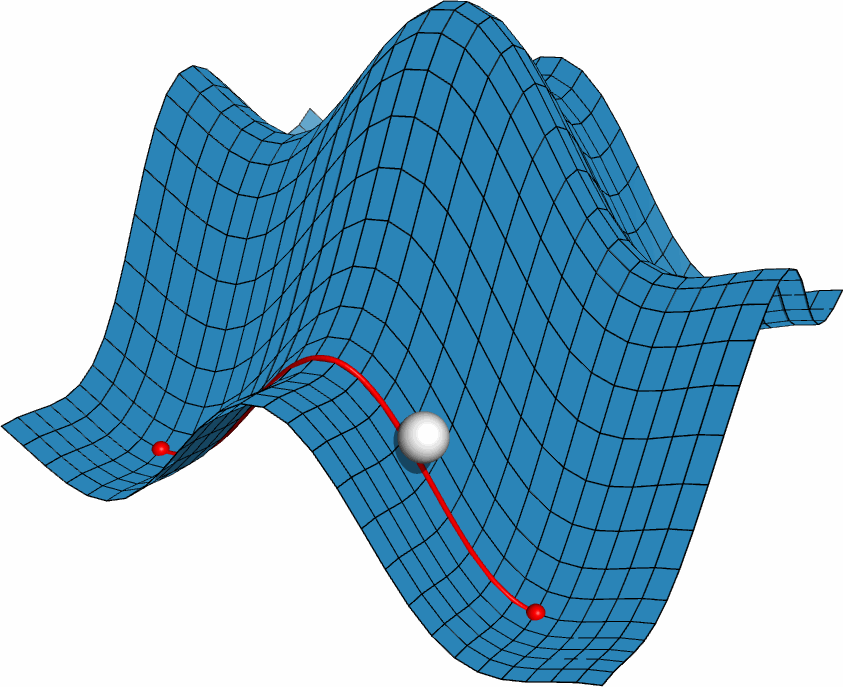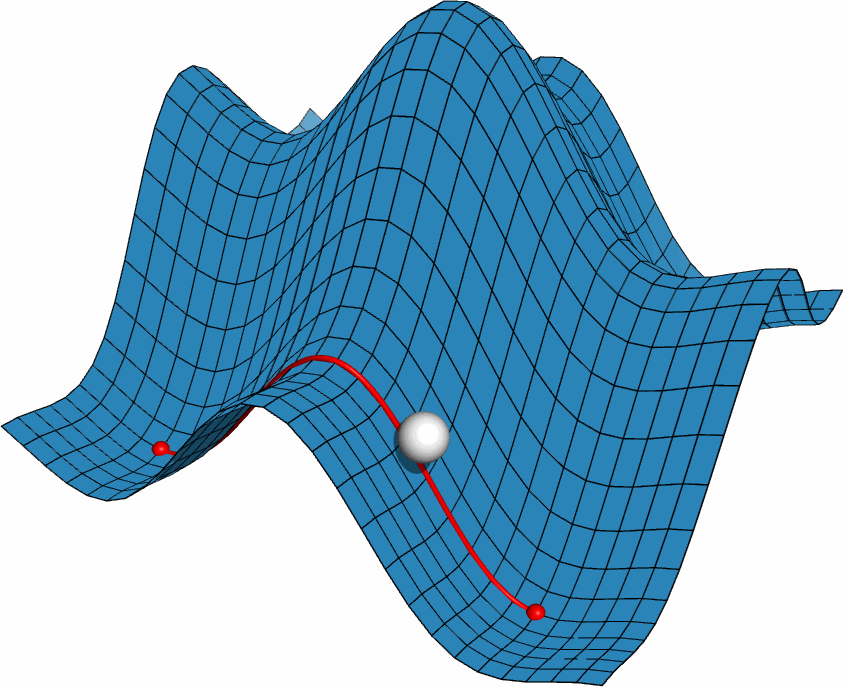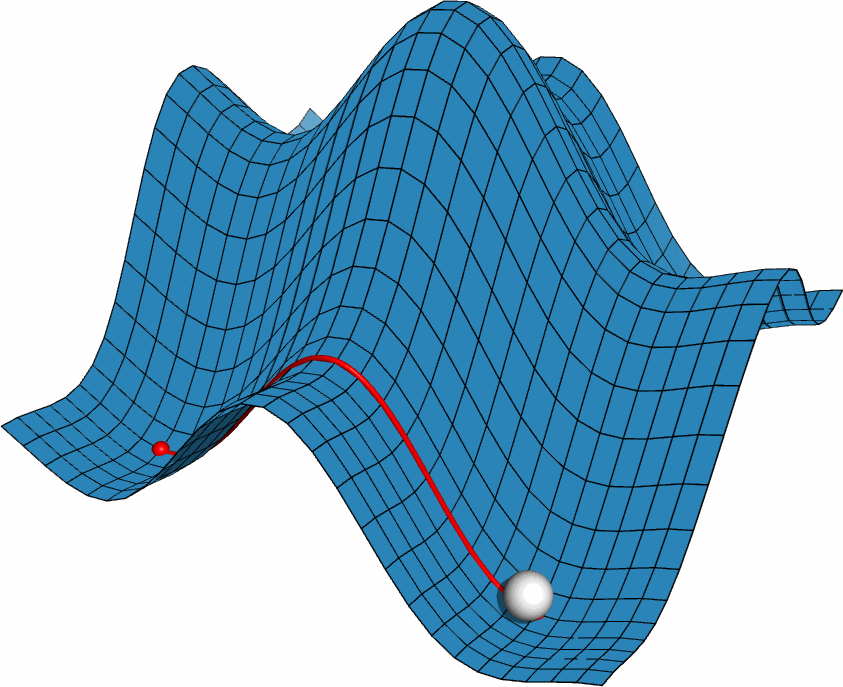
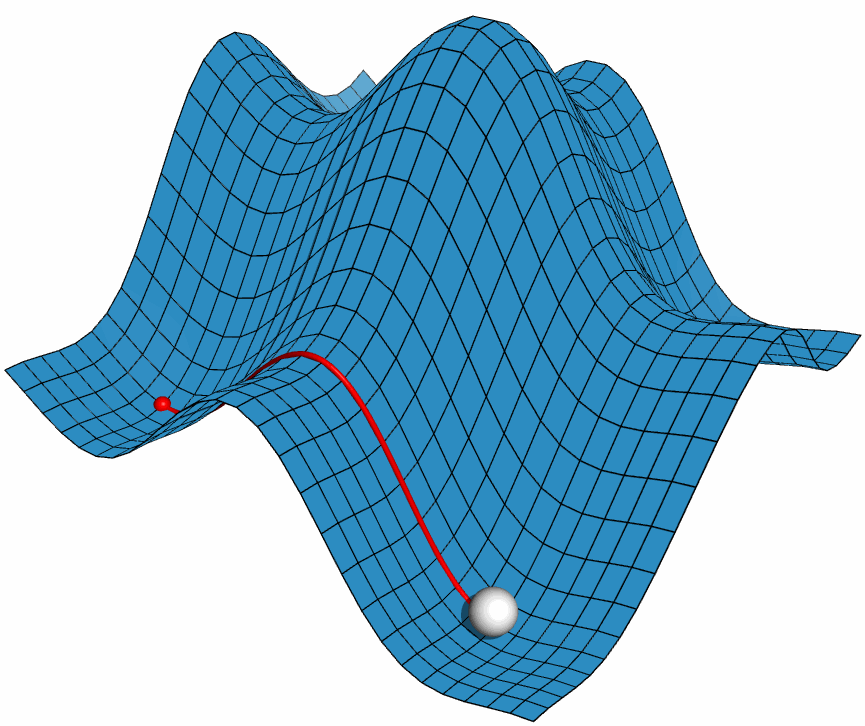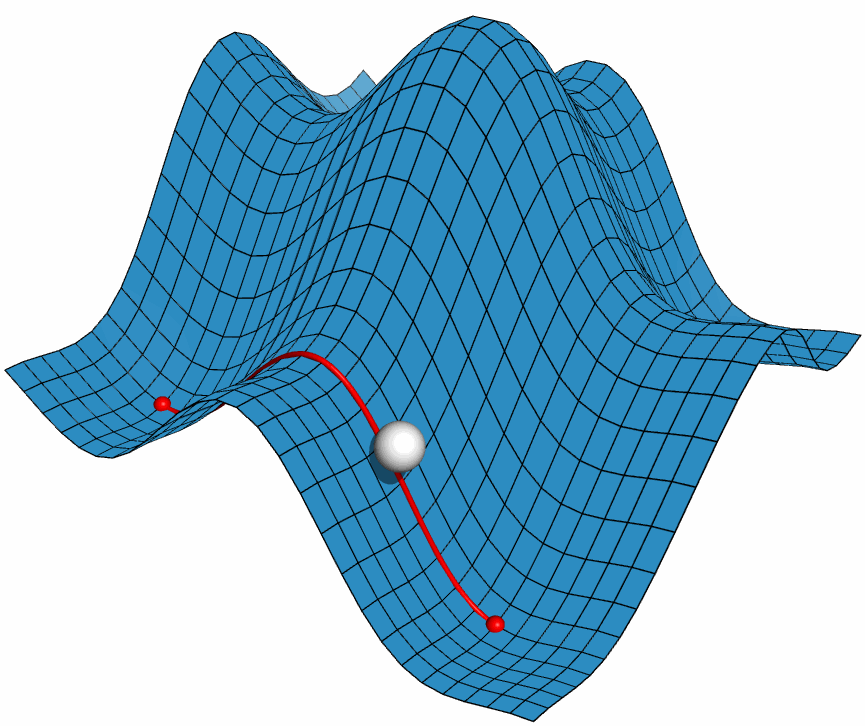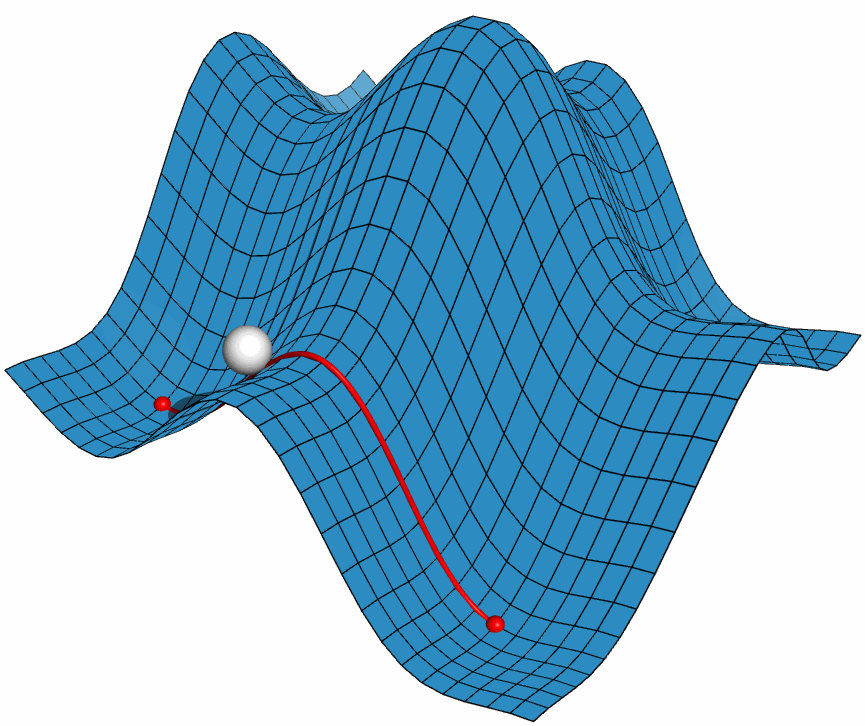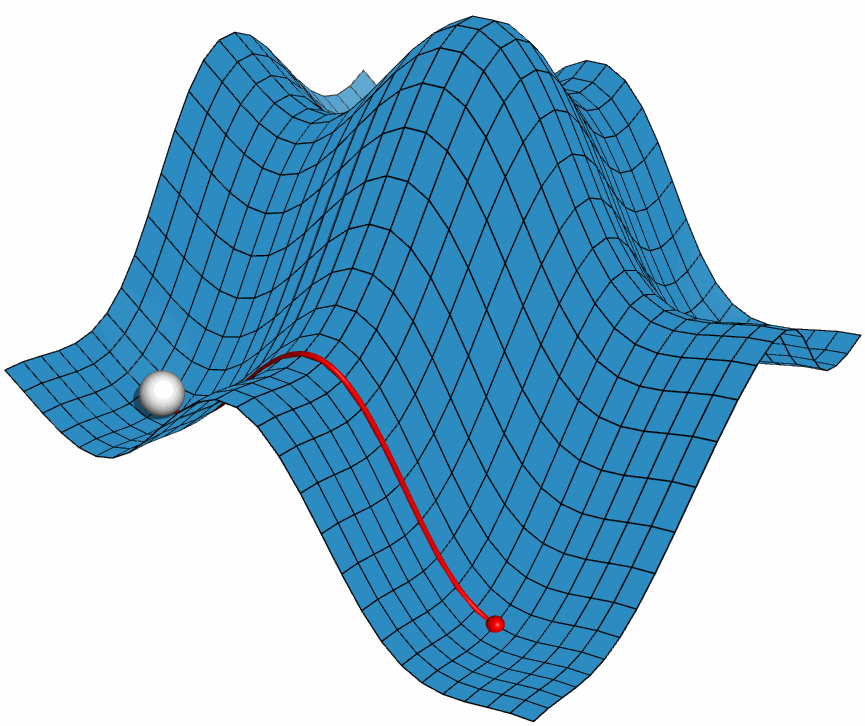
PyMOL是基于Python的分子可视化软件, 在结构生物学中使用十分广泛. 它的主要特色是对生物大分子显示效果好, 并自带一个高效的光线追踪渲染器, 能渲染出逼真的效果. 此外, PyMOL还支持脚本, 可用于精确控制显示, 并提供了一个基本的OpenGL的接口, 以便用户进行一些简单的三维动画设计.
三维建模软件有很多, 不同的软件适用于不同的领域. 最基础的如OpenGL之类, 需要你利用最基本的图元和场景选项一点一点地构建出整个场景. POV-Ray之类则侧重于光线追踪渲染, 并集成了许多可用的模型与场景, 更高级一些. Blender之类则是更通用更专业的三维建模软件, 并非专用于分子建模与可视化. 这样看起来, PyMOL算是处于OpenGL和Blender中间, 集成了POV-Ray的部分功能, 专门用于分子可视化的. 建模时它可以实时可视化, 调试很分方便, 因此对于一些简单的应用很合适.
PyMOL中, 三维模型被称作CGO(Compiled Graphics Objects), 可在其中引用一些OpenGL基本图元. 使用方法和OpenGL很类似, 但由于调用是基于Python的, 所以比直接使用OpenGL简单一些.
下面说说上面两个动画的制作方法.
首先我们需要一个二维势能面的模型. 这个模型最好能够具有一般势能面的特点, 并且包含各类驻点, 如极大点, 极小点, 鞍点. 这就要求势能面上至少有两个极大点. 经过比较, 我发现二元函数 $F(x,y)={\sin x \over x}+{\sin y \over y}$ 满足要求. 但此函数为周期函数, 所以最好加上一个线性项去掉周期性, 并适当调整大小. 最终我用的函数是 $F(x,y)=4({\sin x \over x}+{\sin y \over y})+0.1x$.
确定了势能函数的解析式就可以创建势能曲面了. 方法是最基本的剖分, 用三角面片对整个区间进行剖分, 再将剖分所得的三角面片组合起来. 值得注意的是剖分的方向和三角面片的法向.
至于曲面上球体运动的模拟, 可利用简单的线性步长方法. 若需要更加真实的效果, 则可利用分子动力学中的Verlet积分方法进行计算.
使用方法
- 运行代码:
run PESdemo.py - 背景设为白色:
bg white - 设定光线追踪:
set ray_trace_frames=1 - 输出png图片:
mpng PESdemo
渲染好的图片将输出为PESdemoXXXX.png, XXXX为编号. 利用这些图片就可以制作成动画.
支持动画的图片格式目前主要两种:
-
gif 最常用的, 大家也最熟悉. 各种软件支持最好, 算是通用格式. 可惜只有256色, 失真有时很严重, 特别是对光线追踪渲染过的图片.
-
apng 基于png的动画图片, 效果等同于png. 可惜目前浏览器支持不广, 尚未得到png官方承认.
下面两个图就是这两种格式的对比
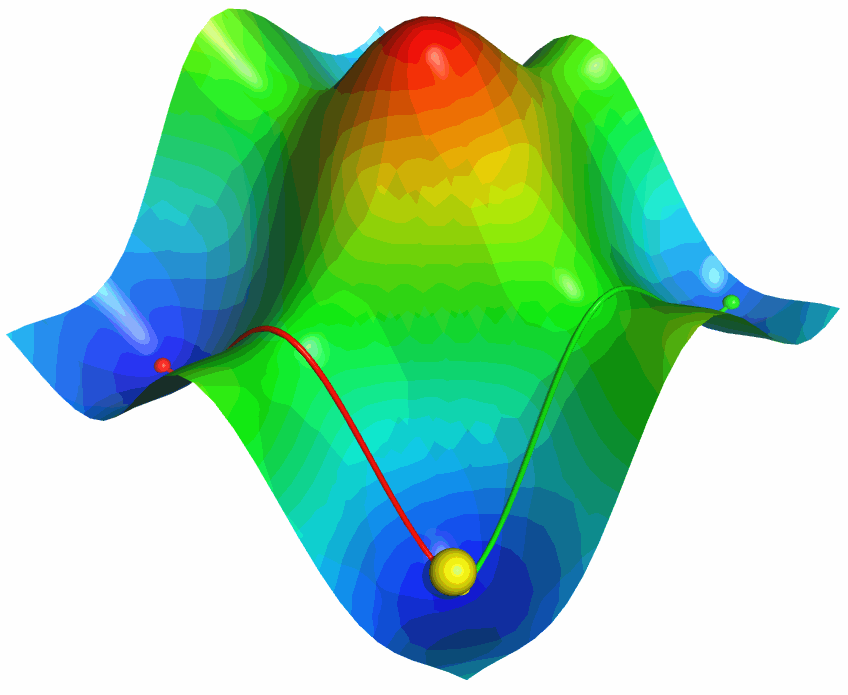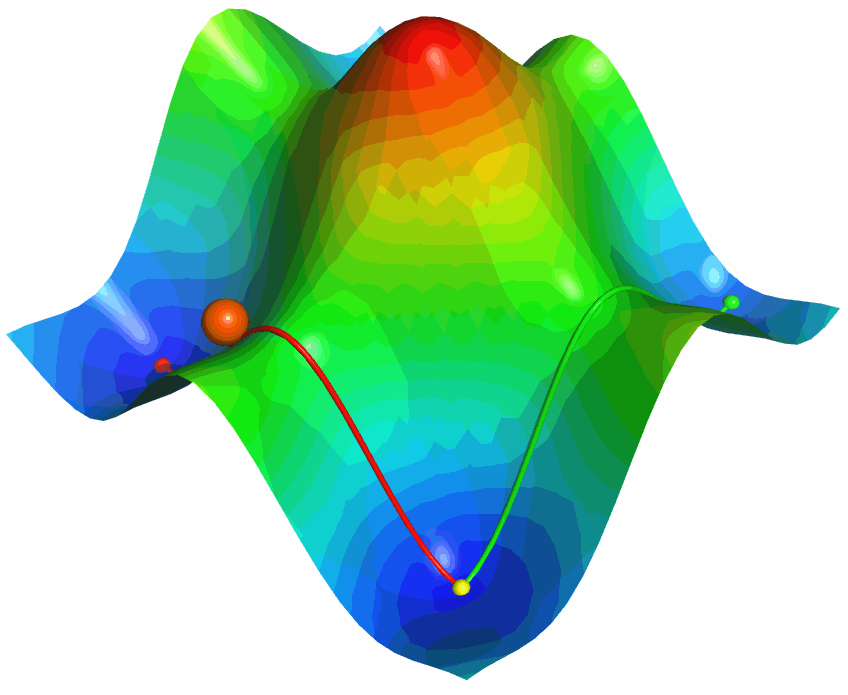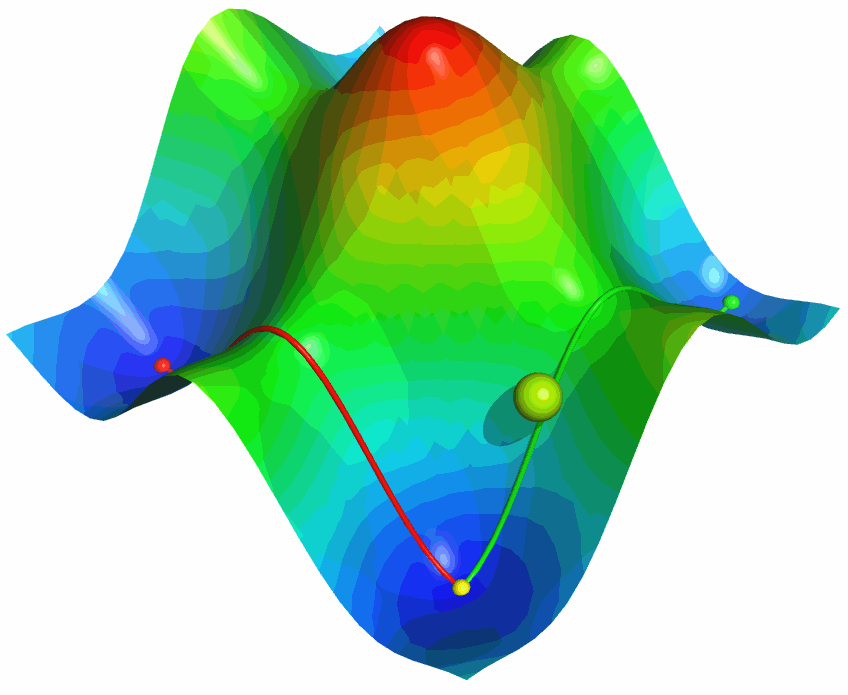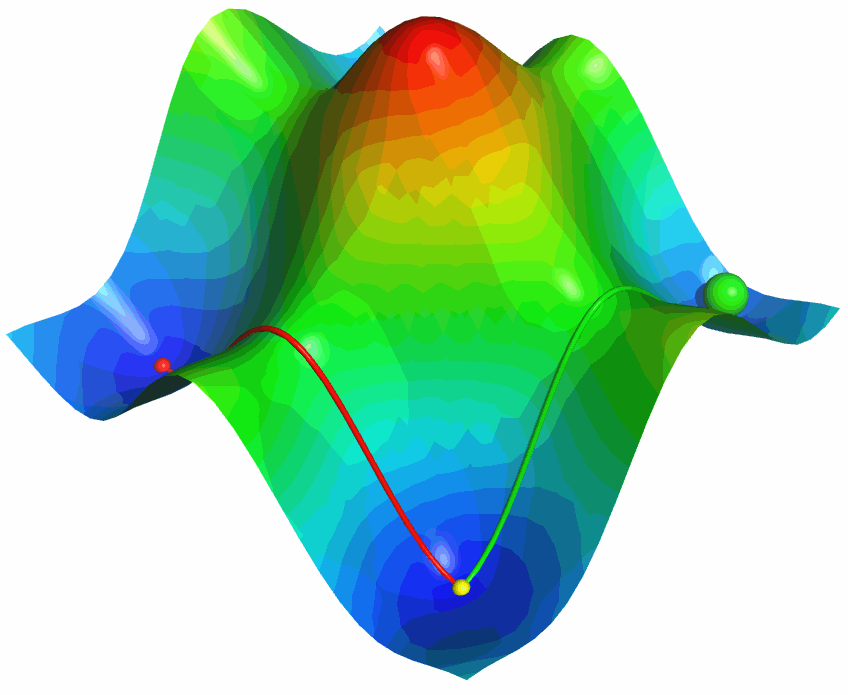
更具体的信息可参考下面的网文:
如果你要使用其他颜色映射方案的话, 可参考我的另一篇博文几种颜色映射方案的解析式.
代码
| PESdemo.py | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 | # coding: utf-8
# ##############################################################################
# 2013-11-14 10:25:11 简单示例
# 2016-09-07 20:23:18 注释, 颜色映射
# ##############################################################################
import math
from pymol import cmd
from pymol.cgo import *
# 势能面函数
def Fxy(x,y):
if x==0: Fx = 4
else: Fx = 4*math.sin(x)/x+.1*x
if y==0: Fy = 4
else: Fy = 4*math.sin(y)/y
return Fx+Fy
# 势能面函数法向
def dFxy(x,y):
if x==0: dFx = 0
else: dFx = 4*(x*math.cos(x)-math.sin(x))/x**2+0.1
if y==0: dFy = 0
else: dFy = 4*(y*math.cos(y)-math.sin(y))/y**2
Rtmp = 1/math.sqrt(dFx*dFx+dFy*dFy+1)
return -dFx*Rtmp, -dFy*Rtmp, Rtmp
def RGB(V, Vmin, Vmax):
dV=Vmax-Vmin; x=(V-Vmin)/dV
r=1; g=1; b=1
if x<0.25: r = 0; g = 4*x
elif x<0.50: r = 0; b = 2-4*x
elif x<0.75: r = 4*x-2; b = 0
else: g = 4-4*x; b = 0
r=min(max(r,0), 1)
g=min(max(g,0) ,1)
b=min(max(b,0) ,1)
return r, g, b
# 是否使用法向, 显示网格, 颜色映射, 使用Verlet方法计算轨迹
YesNorm=1; YesGrid=1; YesMap=0; YesTrj=1
Xini = 4.5 # 小球初始位置
Xmin = -7; Xmax = 5.5; dX = .5; Nx = int((Xmax-Xmin)/dX)
Ymin = -7; Ymax = 7; dY = .5; Ny = int((Ymax-Ymin)/dY)
X = [ 0 for i in range(Nx) ]
Y = [ 0 for j in range(Ny) ]
Z = [ [0]*Ny for i in range(Nx) ]
Zx= [ [0]*Ny for i in range(Nx) ]
Zy= [ [0]*Ny for i in range(Nx) ]
Zz= [ [1]*Ny for i in range(Nx) ]
for i in range(Nx): X[i] = Xmin+dX*i
for j in range(Ny): Y[j] = Ymin+dY*j
for i in range(Nx):
x=X[i]
for j in range(Ny):
y=Y[j]
Z[i][j] = Fxy(x,y)
if YesNorm: Zx[i][j], Zy[i][j], Zz[i][j] = dFxy(x,y)
# 获取极值, 用于颜色映射
Zmin=min(min(Z)); Zmax=max(max(Z))
PES = []
# 绘制网格
if YesGrid:
PES.extend( [ COLOR, 0, 0, 0 ] )
for i in range(Nx):
PES.extend( [ BEGIN, LINE_STRIP ] )
for j in range(0,Ny):
PES.extend( [ NORMAL, Zx[i][j], Zy[i][j], Zz[i][j] ] )
PES.extend( [ VERTEX, X[i], Y[j], Z[i][j] ] )
PES.append( END )
for j in range(Ny):
PES.extend( [ BEGIN, LINE_STRIP ] )
for i in range(Nx):
PES.extend( [ NORMAL, Zx[i][j], Zy[i][j], Zz[i][j] ] )
PES.extend( [ VERTEX, X[i], Y[j], Z[i][j] ] )
PES.append( END )
# 绘制表面
PES.extend( [ COLOR, .19, .6, .83 ] )
for j in range(Ny-1):
PES.extend( [ BEGIN, TRIANGLE_STRIP ] )
for i in range(Nx):
if YesMap:
r, g, b=RGB(Z[i][j+1], Zmin, Zmax)
PES.extend( [ COLOR, r, g, b ] )
PES.extend( [ NORMAL, Zx[i][j+1], Zy[i][j+1], Zz[i][j+1] ] )
PES.extend( [ VERTEX, X[i], Y[j+1], Z[i][j+1] ] )
if YesMap:
r, g, b=RGB(Z[i][j], Zmin, Zmax)
PES.extend( [ COLOR, r, g, b ] )
PES.extend( [ NORMAL, Zx[i][j], Zy[i][j], Zz[i][j] ] )
PES.extend( [ VERTEX, X[i], Y[j], Z[i][j] ] )
PES.append( END )
# 绘制路径
PES.extend( [ LINEWIDTH, 5 ] )
PES.extend( [ BEGIN, LINE_STRIP ] )
PES.extend( [ COLOR, 1., 0., .0 ] )
x = -Xini; y = -Xini
while y<=Xini:
z = Fxy(x,y)
dFx, dFy, dFz = dFxy(x,y)
PES.extend( [ NORMAL, dFx, dFy, dFz ] )
PES.extend( [ VERTEX, x, y, z ] )
y = y+0.1
PES.append( END )
PES.extend( [ BEGIN, LINE_STRIP] )
PES.extend( [ COLOR, 0, 1., .0 ] )
x = -Xini; y = -Xini
while x<=Xini:
z = Fxy(x,y)
dFx, dFy, dFz = dFxy(x,y)
PES.extend( [ NORMAL, dFx, dFy, dFz ] )
PES.extend( [ VERTEX, x, y, z ] )
x = x+0.1
PES.append( END )
# 绘制小球
x = -Xini; y = -Xini; z = Fxy(x,y)
PES.extend ( [ COLOR, 1, 1, 0 ] )
PES.extend ( [ SPHERE, x, y, z, .2 ] )
x = -Xini; y = Xini; z = Fxy(x,y)
PES.extend ( [ COLOR, 1, 0, 0 ] )
PES.extend ( [ SPHERE, x, y, z, .2 ] )
x = Xini; y = -Xini; z = Fxy(x,y)
PES.extend ( [ COLOR, 0, 1, 0 ] )
PES.extend ( [ SPHERE, x, y, z, .2 ] )
cmd.load_cgo(PES, 'PES')
# 模拟小球运行
Rsph = 0.5
if not YesTrj:
x = -Xini
for Ifrm in range(30):
y = -Xini+Ifrm*0.3; z = Fxy(x,y)
dFx, dFy, dFz = dFxy(x,y)
SYS = [ COLOR, 1, 1-Ifrm/30., 0 ]
SYS.extend( [ SPHERE, x+Rsph*dFx, y+Rsph*dFy, z+Rsph*dFz, Rsph ] )
cmd.load_cgo(SYS, 'SYS', Ifrm)
y = -Xini
for Ifrm in range(30):
x = -Xini+Ifrm*0.3; z = Fxy(x,y)
dFx, dFy, dFz = dFxy(x,y)
SYS = [ COLOR, 1-Ifrm/30., 1, 0 ]
SYS.extend( [ SPHERE, x+Rsph*dFx, y+Rsph*dFy, z+Rsph*dFz, Rsph ] )
cmd.load_cgo(SYS, 'SYS', Ifrm+30)
else:
# 初始位置和速度
x = -Xini; y=-Xini
vx = 3.28; vy = 0; Nfrm=130
vx = 0; vy = 3.15; Nfrm=120
dt = 0.05; E0 = 0.5*(vx*vx+vy*vy)+Fxy(x,y)
dFx0, dFy0, dFz0 = dFxy(x,y)
for Ifrm in range(Nfrm):
SYS = [ COLOR, 1, 1, 1 ]
x = x + (vx + 0.5*dFx0*dt)*dt;
y = y + (vy + 0.5*dFy0*dt)*dt;
z = Fxy(x,y)
dFx, dFy, dFz = dFxy(x,y)
SYS.extend( [ SPHERE, x+Rsph*dFx, y+Rsph*dFy, z+Rsph*dFz, Rsph ] )
cmd.load_cgo(SYS, 'SYS', Ifrm)
vx = vx+0.5*(dFx0+dFx)*dt
vy = vy+0.5*(dFy0+dFy)*dt
E = 0.5*(vx*vx+vy*vy)
Rtmp = math.sqrt(2.*abs(E0-z)/(vx*vx+vy*vy))
vx = vx*Rtmp; vy = vy*Rtmp
dFx0, dFy0 = dFx, dFy
cmd.reset()
cmd.zoom('PES', 1.0)
cmd.clip('far', -10.0)
cmd.turn('z', 30)
cmd.turn('x', -60)
cmd.mplay()
|
