2013-08-04 15:20:43
计算方差时需要对平方进行累加, 因此, 有时会出现数值不稳定和溢出的问题. 好的算法在于能尽量避免这些问题.
简单算法
利用定义
方差 \(\sigma^2 =< x^2 >-< x >^2 = \bar {x^2}-{\bar x}^2 ={1 \over N} \sum\limits_{i=1}^N x_i^2 - {1 \over N^2} (\sum\limits_{i=1}^N x_i)^2\)
无偏方差 $s^2 = {N \over N-1}\sigma^2$
- 优点:简单, 只须扫描一遍数据
- 缺点:当相减的两个数值很接近时, 会损失精度; 当标准差远小于平均值时, 精度更差
两步法
先计算出平均值, 再计算方差
$\bar x = { 1\over N }\sum\limits_{i=1}^N x_i$
$\sigma^2={ 1\over N }\sum\limits_{i=1}^N(x_i-\bar x)^2$
- 优点:计算稳定, 除非N很大
- 缺点:需要扫描两遍数据; 当大部分数据接近平均值, 少量数据严重偏离平均值时, 精度差
上两种算法都存在舍入误差累积问题
校正两步算法(Corrected Two-pass Algorithm)或补偿算法(Compensated Algorithm)
\[\sigma^2 = {1 \over N} \sum\limits_{i=1}^N(x_i-\bar x)^2 -{1 \over N^2} [\sum\limits_{i=1}^N(x_i-\bar x)]^2\]若 $\bar x$ 为精确值时, 第二项为零, 否则, 能修正第一项的舍入误差.
- 优点:精确
- 缺点:计算较繁, 须扫描两遍数据
实时/在线算法(Online Algorithm)
当采集数据不能全部保存, 只能读取一次时, 可以使用这种递推方法. 计算时保存平均值与方差
\[\bar x_n = {(n-1) \bar x_{n-1} +x_n \over n} = \bar x_{n-1}+{x_n-\bar x_{n-1}}\] \[\sigma_n^2 = {(n-1)\sigma_{n-1}^2+(x_n-\bar x_{n-1})(x_n-\bar x_n) \over n}\]- 优点:无须保存全部数据
- 确定:精确度低
下面是几种常用软件的方差计算方法
测试数据 1 2 3 4
-
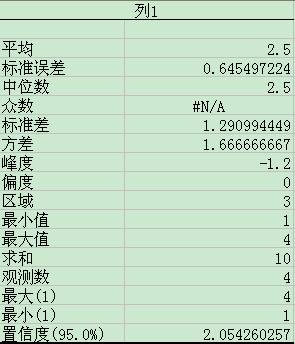
Excel:【工具】==>【数据分析】==>【描述统计】
-
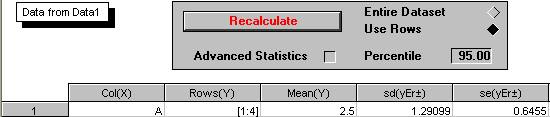
OriginPro 7.5:【Statistics】==>【Descriptive Statistics】==>【Statistics on Columns】
-
MatLab:

对比可知, 这三种软件给出的都是样本方差的无偏估计 $s^2$ 及其相应的标准差.
参考
