- 2013-09-01 18:10:50
- 2016-11-02 10:39:28 修正推导错误
已知晶格常数
\[\alg a&=|\vec a| \\ b&=|\vec b| \\ c&=|\vec c| \\ \alpha&=\vec b \wedge \vec c=\arccos{\vec b \cdot \vec c \over bc} \\ \beta&=\vec a \wedge \vec c=\arccos{\vec a \cdot \vec c \over ac} \\ \gamma&=\vec a \wedge \vec b=\arccos{\vec a \cdot \vec b \over ab} \ealg\]取x轴沿 $\vec a$ 方向, y轴处于 $\vec a \vec b$ 平面内, z轴处于 $\vec a \times \vec b$ 方向, 则晶格矢量
\[\vec a= (a_x, a_y, a_z)=a(1, 0, 0)\] \[\vec b= (b_x, b_y, b_z)=b (\cos\gamma, \sin\gamma, 0)\] \[\vec c= (c_x, c_y, c_z)=c (\cos\beta, {\cos\alpha-\cos\beta\cos\gamma \over \sin\gamma}, {\sqrt{1+2\cos\alpha\cos\beta\cos\gamma-\cos^2\alpha-\cos^2\beta-\cos^2\gamma} \over \sin\gamma})\]设空间某点分数坐标为 $(u, v, w)$, 直角坐标为 $(x, y, z)$, 则
\[\begin{Bmatrix} x \\ y \\z \end{Bmatrix} = \mathbf A \begin{Bmatrix} u \\ v \\w \end{Bmatrix}=\begin{pmatrix} a_x & b_x & c_x \\ a_y & b_y & c_y \\ a_z & b_z & c_z \end{pmatrix} \begin{Bmatrix} u \\ v \\w \end{Bmatrix}\] \[\begin{Bmatrix} u \\ v \\w \end{Bmatrix} = \mathbf A^{-1} \begin{Bmatrix} x \\ y \\x \end{Bmatrix}= \mathbf A^\text{T} \begin{Bmatrix} x \\ y \\x \end{Bmatrix}\]证明
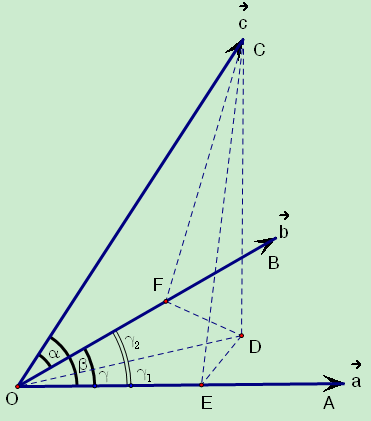
由C点向面OAB做垂线, 交点为D, 连接OD, OD将 $\gamma$ 为 $\gamma_1, \gamma_2$. 作DE垂直于OA, DF垂直于OB, 连接CE, CF, 则CE $\perp$ OA, CF $\perp$ OB.
设OD长度为 $\rho$, 则
\[\rho \cos \gamma_1=c \cos \beta =c_x\] \[\rho \cos \gamma_2=c \cos \alpha\]令 $k={c \over \rho}$, 有
\[\alg \cos \gamma&=\cos(\gamma_1+\gamma_2) \\ &=\cos \gamma_1 \cos\gamma_2-\sin\gamma_1 \sin\gamma_2 \\ &=k^2 \cos\alpha \cos\beta -\sqrt{1-k^2 \cos^2\alpha} \sqrt{1-k^2 \cos^2\beta} \ealg\]可解得
\[k^2=c^2/\rho^2={ \sin^2\gamma \over \cos^2\alpha + \cos^2\beta-2\cos\alpha \cos\beta \cos\gamma }\] \[\rho^2=c^2{ \cos^2\alpha + \cos^2\beta-2\cos\alpha \cos\beta \cos\gamma \over \sin^2\gamma }\]求 $\vec c$ 的分量
x分量 $c_x=c \cos \beta$ 已知
y分量 $c_y = \rho \sin \gamma_1$
\[\alg c_y^2 &= \rho^2 \sin^2\gamma_1 \\ &=\rho^2 (1-\cos^2 \gamma_1) \\ &= \rho^2 (1-c^2 \cos^2\beta/\rho^2) \\ &= \rho^2 -c^2 \cos^2\beta \\ &= c^2 \left[ {\cos^2\alpha + \cos^2\beta-2\cos\alpha \cos\beta \cos\gamma \over \sin^2\gamma} -\cos^2\beta \right] \\ &= c^2 {(\cos\alpha-\cos\beta\cos\gamma)^2 \over \sin^2\gamma } \ealg\]若取 $\alpha \lt \beta$, 则开方取正号
\[c_y=c{ \cos\alpha-\cos\beta\cos\gamma \over \sin\gamma }\]z分量
\[\begin{split} c_z^2 &=c^2-c_x^2-c_y^2 \\ &=c^2 -c^2 \cos^2\beta - \rho^2 + c^2 \cos^2\beta \\ &=c^2-\rho^2 \\ &=c^2\left[ 1- {\cos^2\alpha+\cos^2\beta-2\cos\alpha \cos\beta \cos\gamma \over \sin^2\gamma} \right] \\ &=c^2 {1-\cos^2\gamma-\cos^2\alpha-\cos^2\beta+2\cos\alpha \cos\beta \cos\gamma \over \sin^2\gamma} \end{split}\]由上面所得公式, 我们亦可得到平行六面体的体积
\[\begin{split} V&=abc_z\sin\gamma \\ &=abc\sqrt{1-\cos^2\gamma-\cos^2\alpha-\cos^2\beta+2\cos\alpha \cos\beta \cos\gamma} \\ &=\begin{vmatrix} \vec a \cdot \vec a & \vec a \cdot \vec b & \vec a \cdot \vec c \\ \vec b \cdot \vec a & \vec b \cdot \vec b & \vec b \cdot \vec c \\ \vec c \cdot \vec a & \vec c \cdot \vec b & \vec c \cdot \vec c \end{vmatrix}^{1/2} \\ &=\begin{vmatrix} a^2 & ab\cos\gamma & ac\cos\beta \\ ab\cos\gamma & b^2 & bc\cos\alpha \\ ac\cos\beta & bc\cos\alpha & c^2 \end{vmatrix}^{1/2} \end{split}\]此式多有论述, 不赘述.
