微通道板出射电子云团的弹道模型

2013-09-04 10:40:43 感谢博士生赵爱荣整理此文

2013-10-13 18:40:54 补注

摘要: 在基于微通道板(MCP)的楔条形光子计数探测器中, 从MCP中输出的电子云团到达接收阳极的大小直接影响探测器的成像线性和分辨率, 而电子云团的大小又与MCP-阳极的板间电压, 板间距有着重要的关系.本文分析了电子云团在MCP-阳极之间的运动过程, 并介绍如何利用弹道模型计算电子云团的大小与各参量之间的关系, 为设计MCP提供相应的理论基础. 关键词: 微通道板 楔条型阳极 弹道模型

一、背景简介

在许多实验室科研活动和空间探测项目中, 人们都需要对光信号或粒子进行探测.当被探测光辐射强度很大时, 探测器每秒钟接收大量光子, 可认为光显连续性; 当被探测的光辐射极微弱时, 探测器接收到的将是离散的光子, 光显现出粒子性.

如何对微弱光信号进行探测, 是人们非常关心的问题.目前, 光子计数成像探测技术被认为是探测极微弱光辐射的最好方法. 这种方法所用的光子计数成像探测器能够接收微弱光辐射并将其转换成相应离散的电脉冲信号.

现有的光子计数成像探测器包括雪崩光电二极管阵列、芯片内放大及使用微通道板(MCP,M icrochannel Plate)像增强器的光子计数探测器. 前两种探测器在可见光和近红外波段有很高的量子效率, 但还不能用于紫外到软X射线波段; 后一种探测器在可见光和近红外波段的量子效率只有前两种的25%到50%, 但可用于从紫外到硬X射线波段, 甚至可用于电子、离子、粒子及X射线和宇宙射线的探测.

使用微通道板的光子计数成像探测器通常由前表面镀有光电阴极材料的像增强器、周期性的金属读数电极(称为阳极)和相关的读数电路组成. 根据所用读数阳极的不同, 光子计数成像探测器可分为以下几种: 多阳极微通道板阵列(MAMA)探测器、楔条形阳极(WSA)探测器、电阻阳极(RAE)探测器、延迟线阳极(DLA)探测器和Vernier阳极探测器等.

二、基于楔条形阳极的微通道板光子计数成像探测器

略

2.1 微通道板

微通道板由多个相互平行的微小空心玻璃管阵列构成, 每一个空心管道相当于一个电子倍增器,其直径约为10～100μm, MCP的长径比（长径比即微通道长度与微通道直径的比值）为40～100. 为了提供良好的接触面以便使MCP工作在高压状态下, 微通道板的外环为一圈镀有镍铬金属薄膜的实体边. 对于大开口面积和超薄的微通道板来说, 实体边可以起到提高机械强度的作用.

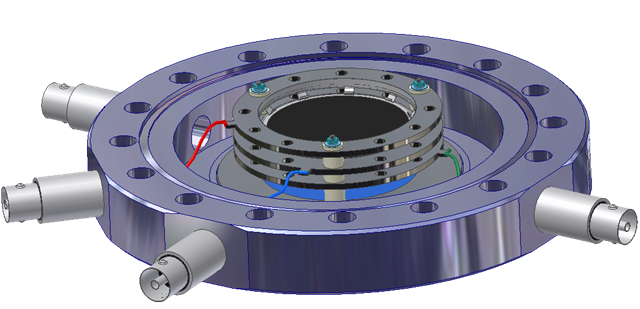
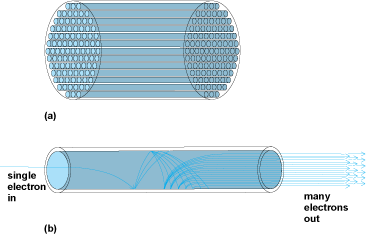
当MCP处于工作状态时, 两端加有负高压, 从而在其两端面形成电场. 当电子、带电粒子或光子等以一定能量撞击到MCP靠近输入面的内壁时, 镀有二次电子发射材料的内壁就会被激发出二次电子. 二次电子在场强的作用下沿着通道向MCP的输出端加速前进, 途中不断撞击微通道内壁并激发出更多的二次电子, 最终在输出端出射大量电子, 从而实现电子倍增.

二次电子发射过程可以分三步来描述: 1）材料吸收一次电子的能量, 体内电子被激发到高能态; 2）被激发到高能态的电子中, 初速指向表面的那一部分向表面运动, 因散射而在运动过程中损失部分能量; 3）到达界面的这些电子如果仍有足够的能量克服表面势垒的能量, 即逸出表面而成为二次电子.

2.2 楔条形阳极

略

2.3 位置读出电路

略

三、影响探测器成像性能的主要因素

对探测器成像性能造成影响的主要因素有: MCP的出射电子云团半径, 电路的性能以及阳极的极间串扰等, 在这些方面需要不断优化以提高探测器的整体性能.

基于MCP的电荷分割读出系统要求事件的电子云团尺寸有一个最佳的范围以达到高的空间分辨率和好的成像线性．对于楔条形阳极(WSA)探测器WSA, 若电子云团的大小为一个周期或者更小, 则电极上收集到的电子云团就可能不与中心位置成线性, 计算出的中心位置与实际中心位置不一致, 从而发生调制．一般消除调制畸变的方法是加大电子云的半径. 但是, 如果电子云团半径过大, 电子云团的外部边缘将超出阳极的有效面积, 造成公共电极上收集电荷过多以及部分电荷的丢失, 从而会导致成像边缘的畸变, 减小探测器的有效面积, 这就是”S”畸变. 所以, 要达到较好的成像性能, 就要确定一个合理的电子云团半径尺寸．研究表明, 电子云团半径的大小与加速电压、MCP和阳极间的距离及MCP的工作电压等因素有关．当电子云团从MCP出射, 它的初始大小由产生倍增的通道及其分布决定．改变阳极和MCP间的电压将会改变电场, 从而调节电子云团的扩散半径．在其它因素不变的情况下, 增加或减小阳极和MCP背面的距离也将相应的加大或减小电子云的半径.

四、弹道模型

弹道模型是计算分析电子云团扩散半径的最简单模型. 在此模型中, 电子被视为经典粒子, 且忽略电子间的相互作用与MCP末端的电子扰动,从而各个电子在两极板间的运动是独立的. 在这些近似下, 电子在MCP出射端形成的电子云团分布仅取决于出射电子的能量和角度分布, 利用这一分布函数就可以估计出距离MCP末端任意位置的电子云团的分布情况.

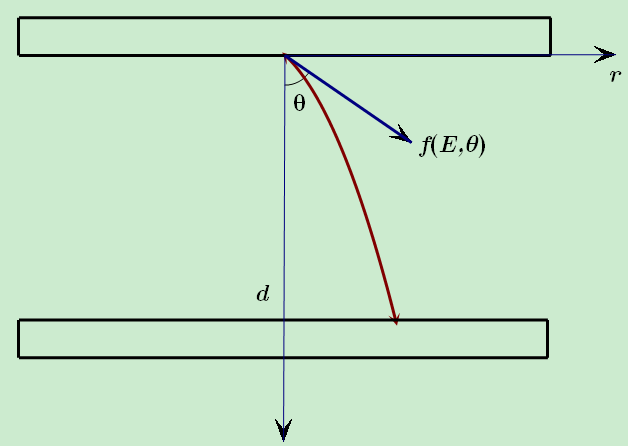
如图所示, 设两板间距为 $d$, 板间电压为 $U$, 从MCP出射的电子的初始动能为 $E$, 出射角度为 $\theta$, 忽略电子间的相互作用, 出射电子的运动方程为:

水平方向: $r = v t \sin\theta$

竖直方向: $d = v t \cos\theta + {1 \over 2} a t^2$

其中, 电子速度大小 \(v=\sqrt{ {2E \over m}}\), 加速度 $a={qU \over m d}$

由上面方程变可求出当电子达到下极板时位置. 由于出射电子的 $E, \theta$ 服从一定的分布, 故电子在下极板上的分布密度并不是均匀的.

实验测得的MCP出射电子的能量和角度分布函数可拟合为(MCP参数: 端电压: 1.4kV, 单孔L/D: 60:1, 孔径: 20μm):

$f(E,\theta) = e^{-\tau^2/2\Delta^2} (A(\tau) e^{-(E-E_0)^2/2\sigma_0^2}+B(\tau)e^{-(E-E_1)^2/2\sigma_1^2})$

其中

此分布函数具有轴对称型, 因此在阳极平板上的电子密度分布也是轴对称的. 下面就来求出这个分布.

将变量由 $(E,\ t)$ 转换为 $(r,\ t)$, 由分布函数的性质

$\int_0^{\pi/2} d\theta \int_0^{\infty} f(E, \theta) dE = \int_0^{\infty} dr \int_0^{t_{max}} f(E, \theta) {\partial(E, \theta) \over \partial(r, t)} dt$

令 $\delta = {1 \over 2} a t^2$, 有

$\theta = \arctan{\tau}=\arctan{r \over d-\delta}, \ E(r,t)={m \over 2t^2}[r^2+(d-\delta)^2]$

则

因此, 电子的分布函数

$F(r, t)=f(E, \theta) m {d+\delta \over t^3}$

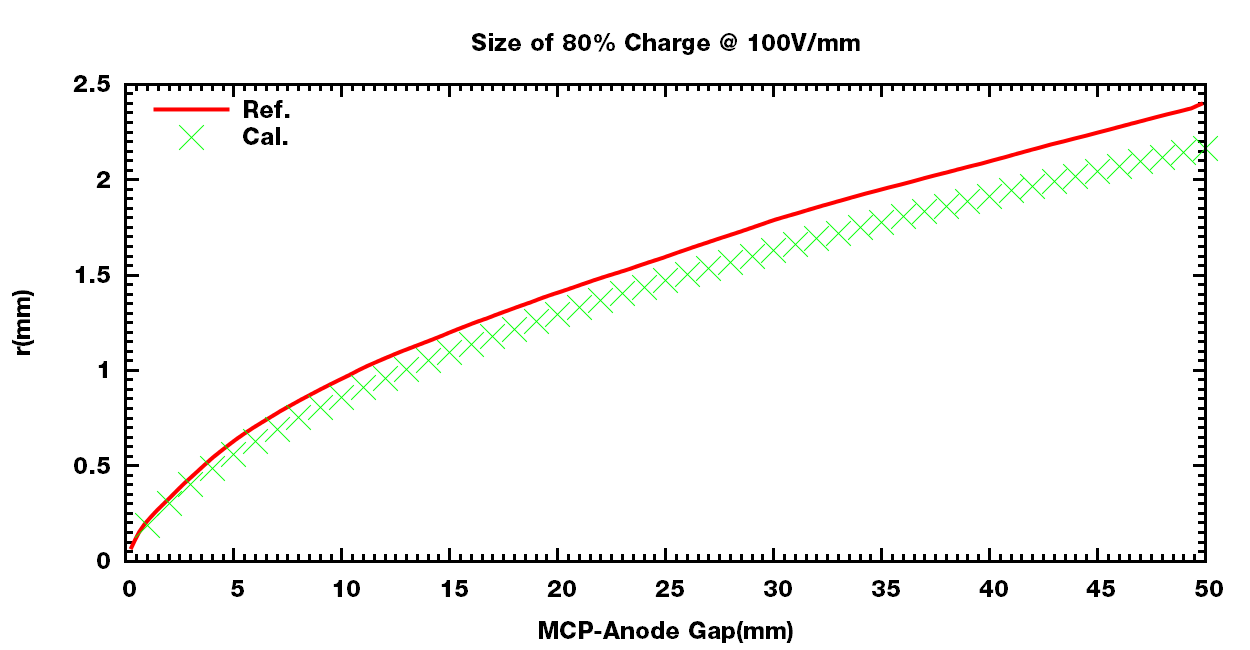
从而, 在极板上$r$ 范围大小内接收的电子百分比为

$\eta = {\int_0^r \int_0^{t_{max}} F(r,t) dr dt \over \int_0^{\infty} \int_0^{tmax} F(r,t) dr dt}$

其中 $t_{max}$ 为电子到达极板所需的最大时间

$t_{max}=\sqrt{2d/a}$

上式给出了设计时所需的极板大小的估计值.

参考

1. A. S. Tremsin, O. H. W. Siegmund. “Spatial distribution of electron cloud footprints from microchannel plates: Measurements and modeling”, Rev. Sci. Instrum., 70(8):3282-3288, 1999
   勘误:
   方程(1)有误, 错把+写为-
   FIG.5. 所绘曲线有误, 计算时使用了方程(1)
2. Go Murakami, Kazuo Yoshioka, Ichiro Yoshikawa. “High-resolution imaging detector using five microchannel plates and a resistive anode encoder”, APPLIED OPTICS, 49(16):2985:2993, 2010
   勘误:
   方程(1)有误, 错为绝对值形式
   Fig.2与Fig.3所绘曲线有误, 因基于方程(1)计算
3. Matlab中几个数值积分函数的比较和优缺点

补注

1. MCP或可看作对昆虫复眼的仿生, 但昆虫复眼皆是弯曲结构, 而我所见MCP都是平面结构. 不知是否可做出弯曲结构MCP? 弯曲结构与平面结构优缺点各在哪里?
2. 弹道模型的计算只取决于MCP出射端电子能量和角度的分布, 因此此分布非常重要. 但文献中是使用的分布仅有1979年实测的一组数据. 此数据长时间没有更新, 不知实测困难在何处. 此模型早被扬弃也未可知.
3. 具体到模型的计算, 实际有三种方法. 另两种如下: 无须进行分布变量的变换, 直接根据 $f(e, \theta)$ 求出 $r$ 的分布. 此法相当于已知某些变量的分布, 求其函数的分布, 最终化为求解积分. 可采用Monte Carlo方法, 随机产生大量电子, 再统计其 $r$ 的分布即可. 此法十分通用, 代码实现亦很简单, 更可方便对模型进行必要修正.
4. 此文公式对端电压为零情形不适用, 须对进行修正.
5. 在分布一定的情况下, 弹道模型最大近似为忽略电子云团中电子之间的相互作用. 若想改进模型, 这是切入点.

代码及实例

# Language: clike
function MCPint()
	global d a m q ecov

	clc;

	m = 9.10938291e-31;       % kg
	q = 1.602176565e-19;      % C
	s2ns = 1.E9;              % ns
	m2mm = 1.E3;              % mm
	acov = m2mm/s2ns^2;
	ecov = 1/(m2mm/s2ns)^2/q;

	Field = 100;              % V/mm
	rmax = 5;                 % mm
	eta = 0.8;                % 80%

	fprintf('%9s %9s\n', 'd', 'r');
	r0=0;
	for d=1:1:50
		a = q*Field*1E3/m *acov;   % mm/ns^2
		tmax = sqrt(2*d/a);        %ns

		norm = quad2d(@F,0,tmax, 0,rmax, ...
					'abstol',1e-6, 'reltol', 1e-6, 'maxfunevals', 4000);

		myfun = @(x) quad2d(@F,0,tmax, 0,x, 'abstol',1e-6, 'reltol', 1e-6, ...
						'maxfunevals', 4000)-eta*norm;

		r=fsolve(myfun,[r0], optimset('Display','off'));
		r0=r;

		fprintf('%9.6f %9.6f\n', d, r);
	end
end
%%
function y = F(t, r)
	global d  a m q ecov

	Rtmp = 0.5*a*t.^2;
	E = 0.5*m*( (d-Rtmp).^2 + r.^2 )./t.^2 ;
	E = E*ecov;                              % eV

	tau = r./(d-Rtmp);

	naninf = (find(isnan(E)   | isinf(E)));   E(naninf) = 0;
	naninf = (find(isnan(tau) | isinf(tau))); tau(naninf) = 0;

	y = f(E, tau).*(d+Rtmp)./t.^3;
	naninf = (find(isnan(y) | isinf(y))); y(naninf) = 0;
	max = (find(Rtmp>d)); y(max) = 0;
end
%%
function y = f(E, tau)

	E0 = 3;
	sgm0 = 12;
	Delt = 0.2;

	min = (find(tau<-100)); tau(min) = 0;

	E1 =   314.45*exp(-6.9515*tau);
	sgm1 = 147.62*exp(-9.7077*tau);

	A = 7.3822*tau - 0.5*(E-E0).^2/sgm0^2;
	B = 9.8642*tau - 0.5*(E-E1).^2./sgm1.^2;

	max = (find(A>100)); A(max) = 0;
	max = (find(B>100)); B(max) = 0;

	y1 = 50.398*exp(A);
	y2 = 25.992*exp(B);

	y = exp(-0.5*tau.^2/Delt^2) .* (y1+y2);
end