2013-11-20 10:37:38
卷积(convolution)是信号处理中一个重要概念, 与其相应的另一个概念是相关(correlation). 它们的英文很类似, 定义也很类似. 卷积研究和过去的关系, 相关则研究与将来的联系, 当时间反向时, 相关就变成了卷积.
卷积 $f(t) \otimes g(t)=\int_{-\infty}^{\infty} f(\tau)g(t-\tau) d\tau$
相关 $f(t) \circledast g(t)=\int_{-\infty}^{\infty} f(\tau)g(t+\tau) d\tau$
关系 $f(t) \otimes g(t) = f(-t) \circledast g(t)$
此文中我们只关注卷积.
卷积的定义
\[\begin{split} h(t)&=f(t) \otimes g(t) \\ &=\int_{-\infty}^{\infty} f(\tau)g(t-\tau) d\tau \\ &=\int_{-\infty}^{\infty} g(\tau)f(t-\tau) d\tau \\ &=g(t) \otimes f(t) \end{split}\]指数函数与高斯函数的卷积
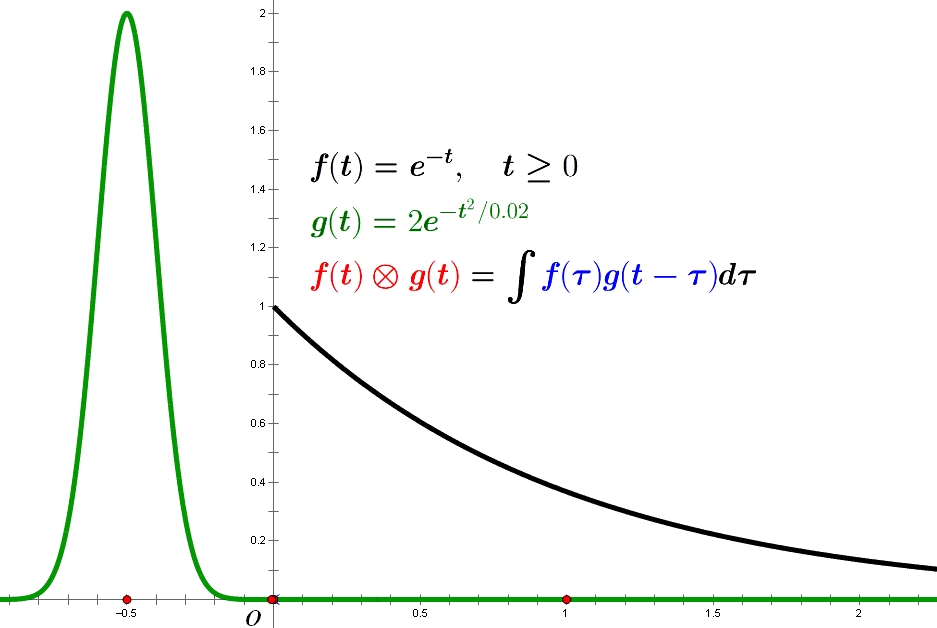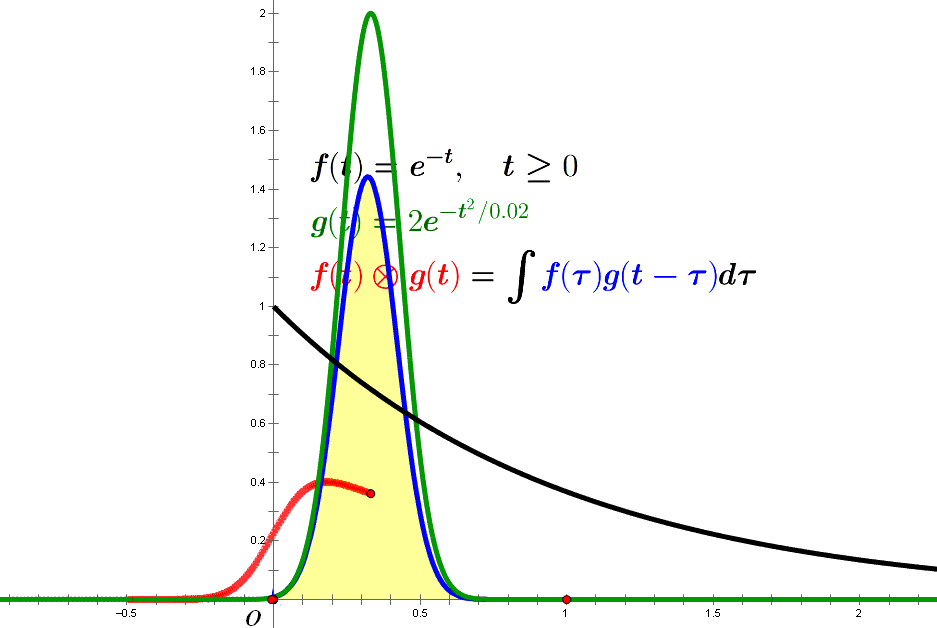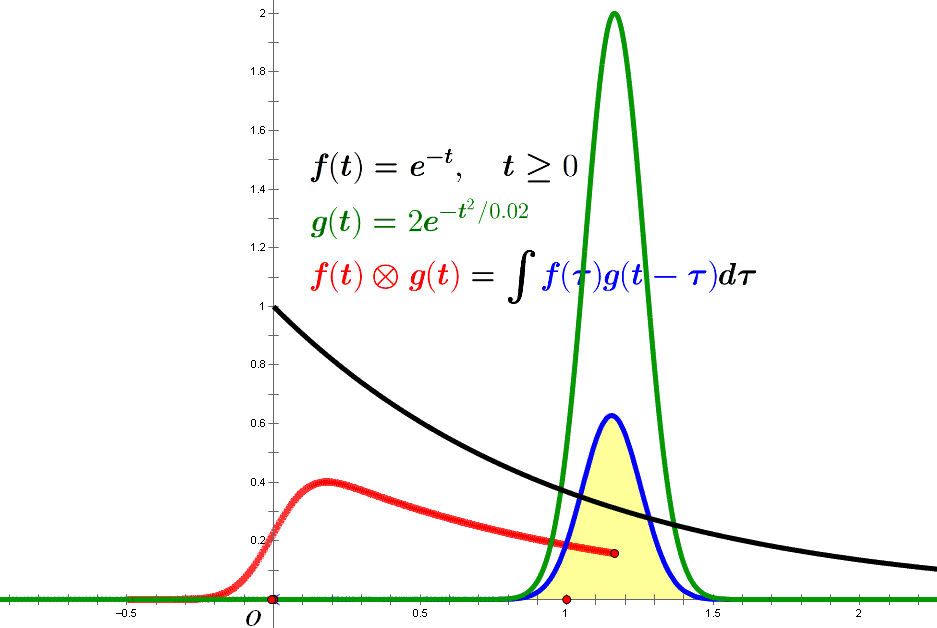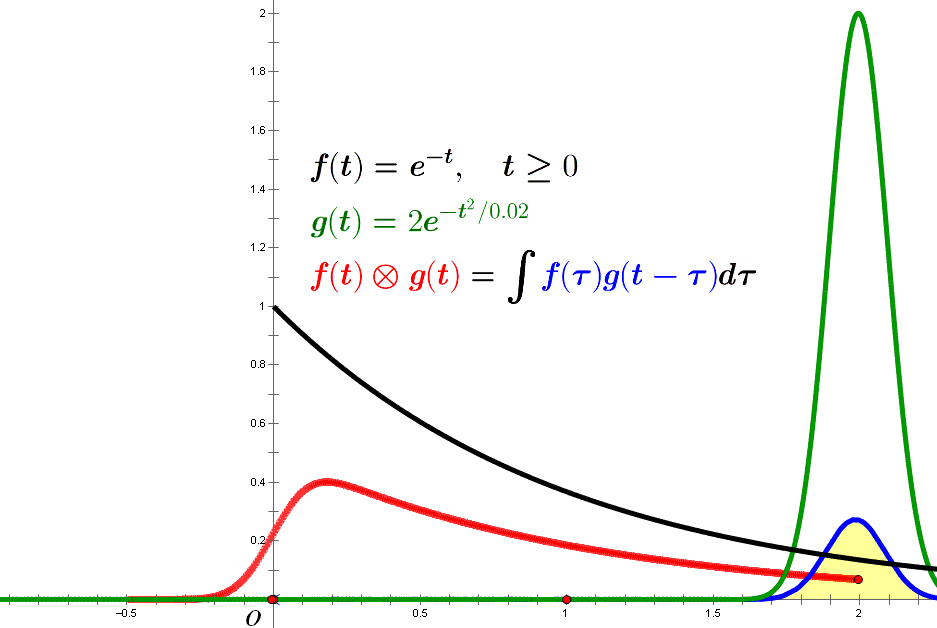
若 $f(t)=A e^{-\alpha t}, g(t)={1 \over \sqrt{2 \pi} \sigma}e^{-(t-t_0)^2/2\sigma^2}$, 则
\[\begin{split} h(t) &=f(t) \otimes g(t) \\ &={A \over \sqrt{2 \pi} \sigma} \int e^{-\alpha \tau} e^{-(t-t_0-\tau)^2/2\sigma^2} d\tau \\ &={A \over \sqrt{2 \pi} \sigma} \int e^{-\alpha \tau} e^{-(\tau-\tau_0)^2/2\sigma^2} d\tau \; (\tau_0=t-t_0) \\ &={A \over \sqrt{2 \pi} \sigma} e^{-\alpha(\tau_0-\alpha\sigma^2/2)} \int e^{-(\tau-\tau^*)^2/2\sigma^2} d\tau \; (\tau^*=\tau_0-\alpha \sigma^2) \\ &={A \over \sqrt{\pi}} e^{-\alpha(\tau_0-\alpha\sigma^2/2)} \int_{x_{min}}^{x_{max}} e^{-x^2} dx \; (x={\tau-\tau^* \over \sqrt{2} \sigma}) \\ &={A \over 2} e^{-\alpha(t-t_0-\alpha\sigma^2/2)} [\mathrm{erf}(x_{max})-\mathrm{erf}(x_{min})] \\ &={A \over 2} e^{-\alpha(t-t_0-\alpha\sigma^2/2)} \mathrm{erfc}({-t+t_0+\alpha \sigma^2 \over \sqrt{2} \sigma}) \; (\tau \in [0,\infty]) \end{split}\]其中,
\[\begin{split} x_{min}&={\tau_{min}-t+t_0+\alpha \sigma^2 \over \sqrt{2} \sigma} \\ x_{max}&={\tau_{max}-t+t_0+\alpha \sigma^2 \over \sqrt{2} \sigma} \end{split}\]由此, 易知
\[\begin{split} Ae^{-\alpha t} \otimes B e^{-\beta t^2}&={AB \over 2} \sqrt{\pi \over \beta} e^{-\alpha(t-\alpha/4\beta)} \mathrm{erfc}(-\sqrt{\beta}t+\alpha/2\sqrt{\beta}) \\ Ae^{-\alpha t} \otimes {1 \over \sqrt{\pi}}e^{-t^2}&={A \over 2}e^{-\alpha(t-\alpha/4)} \mathrm{erfc}(-t+\alpha/2) \end{split}\]卷积滑动平均的含义使得它可以和很多其他领域联系起来, 例如配分函数, 自由能.
对NPT模拟, 配分函数
$Q=\lt e^{-\beta E} \gt = \int e^{-\beta E} p(E) dE$
Gibbs自由能
$G=-kT \ln \lt e^{-\beta E} \gt =-{1 \over \beta} \ln Q$
若能量服从正态分布
$p(E)={1 \over \sqrt{2 \pi} \sigma } e^{-(E-E_0)^2/2\sigma^2}$
则
\[\begin{split} Q&={1 \over \sqrt{2 \pi} \sigma } \int e^{-\beta E} e^{-(E-E_0)^2/2\sigma^2} dE \\ &={1 \over \sqrt{2 \pi} \sigma } e^{-\beta (E_0-\beta \sigma^2/2)} \int e^{-(E-E_0+\beta \sigma^2)^2/2\sigma^2} dE \\ &=e^{-\beta (E_0-\beta \sigma^2/2)} \\ G&= -{1 \over \beta} \ln Q =E_0-\beta \sigma^2/2 \end{split}\]当直接加和计算时, 若能量取值范围有限, \(E \in [E_{min}, E_{max}]\), 此时
\[\begin{split} Q&={1 \over \sqrt{2 \pi} \sigma } e^{-\beta (E_0-\beta \sigma^2/2)} \int_{E_{min}}^{E_{max}} e^{-(E-E_0+\beta \sigma^2)^2/2\sigma^2} dE \\ &= {1 \over \sqrt{\pi}} e^{-\beta (E_0-\beta \sigma^2/2)} \int_{t_{min}}^{t_{max}} e^{-t^2} dt \; (t={E-E_0+\beta \sigma^2 \over \sqrt{2} \sigma}) \\ G&=E_0-{\beta \sigma^2 \over 2} -{1 \over \beta } \ln I \\ I&= {1 \over \sqrt{\pi}} \int_{t_{min}}^{t_{max}} e^{-t^2} dt ={1 \over 2} [\mathrm{erf}(t_{max})-\mathrm{erf}(t_{min}) ] \end{split}\]$\ln I$ 可用Wolfram Alpha求解, 但仅限于整数.
