样条函数插值拟合|Jerkwin

2014-02-11 09:26:49

在拟合势能函数的时候, 除解析式外, 也可以利用样条函数进行拟合. 样条拟合与其插值正好相反: 已知函数在节点上的值求任意位置的值, 做插值; 已知函数的某些组合值求函数节点上的值, 属于拟合. 由于样条函数可以化为节点函数值的线性表达式, 这样就可以将待求参数线性化, 得到最优情况下函数的形状, 为寻找合适的解析式提供依据, 当然也可以直接利用得到的离散数据拟合解析式.

样条函数可以是零阶, 一阶, 二阶, 三阶或更高阶. 实际使用中, 三阶使用最为普遍. 由于三次样条的构造需要求解一个三对角线性方程组, 其显式解很难得到, 所以线性化结果很繁琐.

零阶

在每一区间上样条函数为常量, 函数整体呈台阶状. 对等距情况, 计算时最好使用就近原则, 取最近点的值作为拟合点, 可用i=nint(x/dx)实现.

一阶

在每一区间上样条函数为线性函数, 函数整体呈折线状.

$f_i(x)=y_i+{y_{i+1}-y_i \over \Delta x} (x-x_i)$

此式自动满足函数值连续条件, 即零阶连续.

二阶

在每一区间上, 样条函数为二次函数, 整体一阶连续, 即有连续的导数. 但仅有节点的函数值不能唯一确定整个函数, 还须提供某一节点上的导数值, 一般可令端点的导数值为零. 二次样条函数在偶数点的曲率不连续. 由二阶开始, 插值函数不再具有局域性, 改变某一节点, 函数整体都会改变. 使得线性系数分离很困难.

\[\begin{align} f_i(x) &=y_i + k_i (x-x_i) + {k_{i+1}-k_i \over 2 \Delta x} (x-x_i)^2 \\ k_{i+1} &=-k_i+2 {y_{i+1}-y_i \over \Delta x}, k_i=2 {y_{i+1}-y_i \over \Delta x}-k_{i+1} \end{align}\]

可化简得

\[\begin{align} f_i(x) &= y_i+k_i(x-x_i) + (y_{i+1}-y_i-k_i \Delta x) ({x-x_i \over \Delta x})^2 \\ &= \alpha^2 y_{i+1} + (1-\alpha^2) y_i + (1-\alpha)\omega k_i \\ \alpha &= \omega/\Delta x, \; \omega=x-x_i \end{align}\]

对势能函数, 一般满足远距离处导数为零, 故可使用自然条件 $k_n=0$ , 由此, 可推知所有系数 $k_i$ .

令 $k_i = {2 \over \Delta x} T_i, \Delta_i=y_{i+1}-y_i$, 则 $T_i$ 满足递推式

$T_i = \Delta_i - T_{i+1}$

可求得

\[\begin{align} T_i = \sum_{j=i}^{n-1} (-1)^{j-i} \Delta_j \end{align}\]

样条函数可写为

$f_i(x)=\alpha^2 y_{i+1} + (1-\alpha^2) y_i + 2\alpha(1-\alpha)T_i, \; \alpha = (x-x_i)/\Delta x$

对不等距划分, 令 $\Delta_i={y_{i+1}-y_i \over x_{i+1}-x_i}$, $k_i$ 满足如下递推式

$k_i = 2 \Delta_i -k_{i+1}$

求得

\[\begin{align} k_i = 2 \sum_{j=i}^{n-1} (-1)^{j-i} \Delta_j \end{align}\]

三阶

对等距划分的均匀样条, 设节点为 $1, 2,….n$, 若 $x \in [x_i, x_{i+1}], a=x-x_i, b=x_{i+1}-x, a+b=h=\Delta x$, 则

\[6 h f_i(x) = 6(a y_{i+1}+b y_i) + a(a^2-h^2)M_{i+1} + b(b^2-h^2)M_i\]

$M_i$ 为节点的二阶导数, 对应于力学上的弯矩, 满足下面的方程

\[M_i + 4 M_{i+1} + M_{i+2} = d_{i+1} = {6 \over h^2} (y_{i+2}-2y_{i+1}+y_i), \\ i=1,2...n-2\]

要求的 $M_i$ 个数为 $n$, 而对应的方程数目为 $n-2$, 故还需两个边界条件才能唯一确定, 边界条件可取为两端点的导数值或是二阶导数值. 常用的自然边界条件指 $M_1=M_n=0$. 加上边界条件后便可求得 $M_2, M_3, ...M_{n-1}$

$M_i$ 满足的方程为

\[\begin{matrix} 0 &+ & 4M_2 &+ & M_3 &= &d_2 \\ M_2 &+ & 4M_3 &+ & M_4 &= &d_3 \\ M_3 &+ & 4M_4 &+ & M_5 &= &d_4 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\ M_{n-3} &+ & 4 M_{n-2} &+ & M_{n-1} &= &d_{n-2} \\ M_{n-2} &+ & 4 M_{n-1} &+ & 0 &= &d_{n-1} \end{matrix}\]

写为矩阵形式

\[\begin{bmatrix} 4 & 1 & 0 & \cdots \\ 1 & 4 & 1 & \cdots \\ \vdots & \vdots & \vdots & \vdots \\ \cdots & 1 & 4 & 1 \\ \cdots & 0 & 1 & 4 \\ \end{bmatrix} \left[ \begin{array}{c} M_2 \\ M_3 \\ \vdots \\ M_{n-2} \\ M_{n-1} \end{array} \right] =\left[ \begin{array}{c} d_2 \\ d_3 \\ \vdots \\ d_{n-2} \\ d_{n-1} \end{array} \right]\]

可见, 此方程为三对角方程组, 对角占优, 存在唯一解, 可利用所谓的追赶法求解. 中文常称的追赶法, 是Thomas方法的形象翻译. 大致求解过程分为两步:

追: 利用消元法将原方程化为二对角方程, 向前递推, 使系数矩阵主对角线变为1. 由第一个方程, 得到 $M_2$ 和 $M_3$ 的关系, 将其带入第二个方程, 消去主对角线下方系数. 以此进行, 最终追到 $M_{n-1}$, 得到其解. 变换后, 其方程为
\[\begin{bmatrix} 1 & A_2 & 0 & \cdots \\ 0 & 1 & A_3 & \cdots \\ \vdots & \vdots & \vdots & \vdots \\ \cdots & 0 & 1 & A_{n-2} \\ \cdots & 0 & 0 & 1 \\ \end{bmatrix} \left[ \begin{array}{c} M_2 \\ M_3 \\ \vdots \\ M_{n-2} \\ M_{n-1} \end{array} \right] =\left[ \begin{array}{c} D_2 \\ D_3 \\ \vdots \\ D_{n-2} \\ D_{n-1} \end{array} \right]\]
赶: $M_{n-1}$ 已经追得, 然后由此倒推, 得到其他 $M_i$ 值.

对上面的方程, 由于系数是固定的, Thomas方法的递推式为

\[\begin{align} A_2 &= {1 \over 4}, & A_i &= {1 \over 4-A_{i-1}} \\ D_2 &= A_2 d_2, & D_i &= A_i(d_i-D_{i-1}) \\ M_{n-1} &= D_{n-1}, & M_i &= D_i-A_i M_{i+1} \end{align}\]

对 $A_i$, 可求得其通式

$A_i=2-\sqrt{3} \dfrac{t^i+1} {t^i-1}, t=(2+\sqrt{3})^2$

对 $D_i$, 向后递推至 $D_2$, 一般项可写为

\[\begin{align} D_j = \sum_{k=2}^j (-1)^{j-k} P_k^j d_k \end{align}\]

对 $M_i$, 向前递推至 $M_{n-1}$, 一般项可写为

\[\begin{align} M_i = \sum_{j=i}^{n-1} (-1)^{j-i} P_i^{j-1} D_j \end{align}\]

综合上面两个结果, 得到

\[\begin{align} M_i &= \sum_{j=i}^{n-1} \sum_{k=2}^j (-1)^{2j-i-k} P_i^{j-1} P_k^j d_k \\ &= \sum_{j=i}^{n-1} \sum_{k=2}^j (-1)^{i+k} P_i^{j-1} P_k^j d_k, \; i=2,3,...n-1 \\ P_m^n &= \prod_{l=m}^n A_l = A_m A_{m+1} \ldots A_{n-1} A_n, \; n>m \\ \end{align}\]

根据插值公式

\[\begin{align} d_k &= {6 \over h^2} (y_{k+1}-2y_k+y_{k-1}) \\ 6 h f_i(x) &= 6(\alpha y_{i+1}+\beta y_i) + \alpha(\alpha^2-h^2)M_{i+1} + \beta(\beta^2-h^2)M_i \end{align}\]

以划分间距 $h$ 为单位, 约化上述公式

\[\begin{align} f_i(x) &= \alpha y_{i+1}+\beta y_i + \alpha(\alpha^2-1)\mu_{i+1} + \beta(\beta^2-1) \mu_i \\ \alpha &={a \over h}, \beta={b \over h}=1-\alpha, \mu_i={M_i \over 6/h^2} \end{align}\]

由此可见, 虽然三次样条函数仍可写为节点值的线性形式, 但其系数十分复杂.

上面公式看起来清楚, 但是实际计算时需要计算 $M_i$ 和 $M_{i+1}$, 两个三重循环, 整体计算量为 $O(N^3)$. 利用 $A_i$ 的近似关系和 $M_i$ 的递推关系可以将公式的计算量减少一些.

\[\begin{align} f_i(x) &= \alpha y_{i+1}+\beta y_i + \alpha(\alpha^2-1)\mu_{i+1} + \beta(\beta^2-1) \mu_i \\ &= \alpha y_{i+1}+\beta y_i + \beta(\beta^2-1) D_i \\ &+ [\alpha(\alpha^2-1)-\beta(\beta^2-1)A_i] \mu_{i+1} \end {align}\]

对不等距划分, 上面的递推公式太过复杂, 很难写出一般项了. 样条函数可写为

\[\begin{align} f_i(x) &= {a y_{i+1} + by_i \over h_i} + {a(a^2-h^2)M_{i+1}+b(b^2-h^2)M_i \over 6h_i} \\ h_i &= x_{i+1}-x_i, a=x-x_i, b=h_i-a \end{align}\]

$M_i$ 满足方程

\[\begin{align} h_i M_i + 2(h_i+h_{i+1}) M_{i+1} + h_{i+1}M_{i+2} \\ = 6( {y_{i+2}-y_{i+1} \over h_{i+1}} - {y_{i+1}-y_i \over h_i} ), \\ i=1,2,\cdots,n-2 \end{align}\]

代码及测试测试结果

awk实现的代码如下

# Language: bash
awk ' BEGIN{ Ndat=0 }
NF==3 { Ndat++; X[Ndat]=$2; Y[Ndat]=$3 }

END {
    for(i=1; i<Ndat; i++) dX[i]=X[i+1]-X[i]
    for(i=2; i<Ndat; i++) d[i]=6*( (Y[i+1]-Y[i])/dX[i] - (Y[i]-Y[i-1])/dX[i-1] )

    A[1]=0; A[Ndat]=0
    D[1]=0; D[Ndat]=0
    for(i=2; i<=Ndat-1; i++) {
        ai=dX[i-1]
        bi=2*(dX[i-1]+dX[i])
        ci=dX[i]
        A[i]=ci/(bi-ai*A[i-1])
        D[i]=(d[i]-ai*D[i-1])*A[i]/ci
    }
    M[Ndat]=0
    for(i=Ndat-1; i>1; i--) M[i]=D[i]-A[i]*M[i+1]

    # for(i=1; i<=Ndat; i++) print i, dX[i], d[i], A[i], D[i], M[i]
    h=X[2]-X[1]
    for(x=X[1]; x<X[Ndat]; x+=.1*h) print x, SP2(x, 0, Ndat, X, Y, dX), SP3(x, 0, Ndat, X, Y, dX, M)
}

function SP2(x, i, Ndat, X, Y, dX,      j,a,ki) {
    if(i==0) {
        for(i=1; i<Ndat; i++) if(X[i+1]>x) break
    }
    ki=0
    for(j=i; j<=Ndat-1; j++) ki += 2*(-1)^(j-i)*(Y[j+1]-Y[j])/dX[j]

    a=(x-X[i])/dX[i]
    return a^2*Y[i+1]+(1-a^2)*Y[i]+(1-a)*ki*(x-X[i])
}
#
function SP3(x, i, Ndat, X, Y, dX, M,       a,b,h) {
    if(i==0) {
        for(i=1; i<Ndat; i++) if(X[i+1]>x) break
    }
    h=dX[i]
    a=x-X[i]; b=h-a
    return (a*Y[i+1]+b*Y[i])/h + ( a*(a^2-h^2)*M[i+1]+b*(b^2-h^2)*M[i] )/(6*h)
}
#
function Psp3(Ndat,     i,j,k,a) {
    a=(2+sqrt(3))^2
    for(i=2; i<Ndat; i++) {
        for(j=i; j<Ndat; j++) {
            P[i,j]=1
            for(k=i; k<=j; k++) P[i,j] *= 2-sqrt(3)*(a^k+1)/(a^k-1)
        }
    }
}
#
function uniSP3(x, i, Ndat, X, Y,       j,k,a,b,h) {
    if(i==0) {
        for(i=1; i<Ndat; i++) if(X[i+1]>x) break
    }

    h=X[2]-X[1]
    a=(x-X[i])/h; b=1-a

    for(j=1; j<=Ndat; j++) Coef[j]=0

    Coef[i]   += b
    Coef[i+1] += a

    Rsec=b*(b^2-1)
    for(k=2; k<=i; k++) {
        Rtmp=Rsec * (-1)^(i-k) * P[k,i]
        Coef[k+1] +=    Rtmp
        Coef[k]   += -2*Rtmp
        Coef[k-1] +=    Rtmp
    }

    Rsec=a*(a^2-1)-b*(b^2-1)*P[i,i]
    for(j=i+1; j<=Ndat-1; j++) {
        Rij=Rsec * (-1)^(i+1)
        if(j!=i+1) Rij *= P[i+1,j-1]
        for(k=2; k<=j; k++) {
            Rtmp=Rij * (-1)^k * P[k,j]
            Coef[k+1] +=    Rtmp
            Coef[k]   += -2*Rtmp
            Coef[k-1] +=    Rtmp
        }
    }

    F=0
    for(j=1; j<=Ndat; j++) F += Coef[j]*Y[j]

    return F #( a*Y[i+1]+b*Y[i] + a*(a^2-1)*Mi(i+1, Ndat) + b*(b^2-1)*Mi(i, Ndat) )
}
#
function Mi(i, Ndat,        j,k,Rtmp,ret) {
    ret=0
    for(j=i; j<=Ndat-1; j++) {
        Rtmp=(-1)^i
        if(j!=i) Rtmp *= P[i,j-1]
        for(k=2; k<=j; k++)
            ret += Rtmp*(-1)^k*P[k,j] *d[k]
    }
    return ret
}

' ABS >ABS.sp
# ' CUB  > CUB.sp
#' LJ  >LJ.sp

利用Matlab的csape函数可以进行三次样条函数的插值, 示例代码如下

# Language: clike
format long

x=1:0.02:15;
y=-1E3*(-12./x.^13+6./x.^7);

pp=csape(x,y,'second',[0,0]);
pp=csape(x,y);
xsp=1:0.01:1.5;
ysp=ppval(pp,xsp);
yst=-1E3*(-12./xsp.^13+6./xsp.^7);

plot(x,y,'o',xsp,ysp,'-',xsp,yst,'-')
axis([1 1.5 -600 600])

FID=fopen('LJ.mat', 'w');
Ndat=length(xsp);
for i=1:Ndat
    fprintf(FID, '%f %f\n', xsp(i), ysp(i));
end

几个测试函数的结果

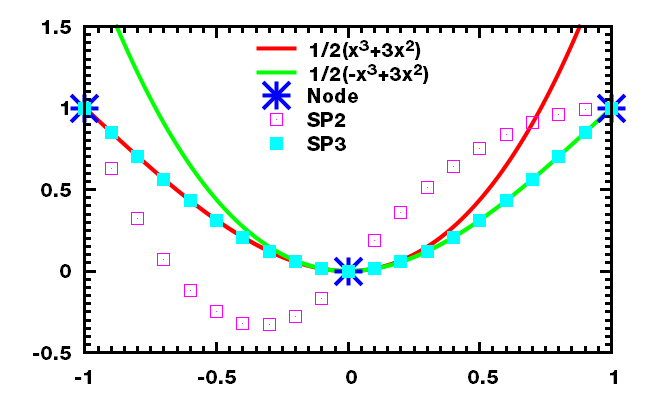
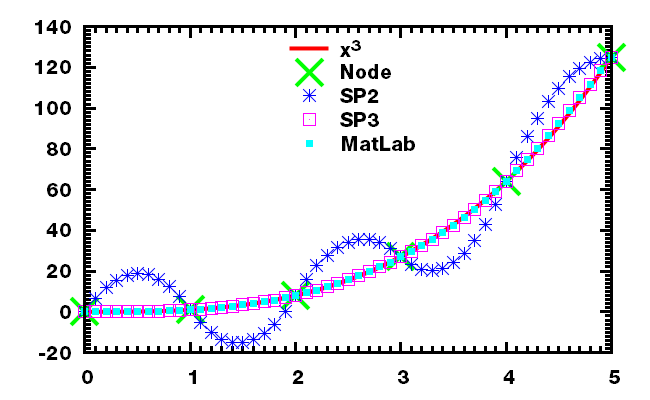
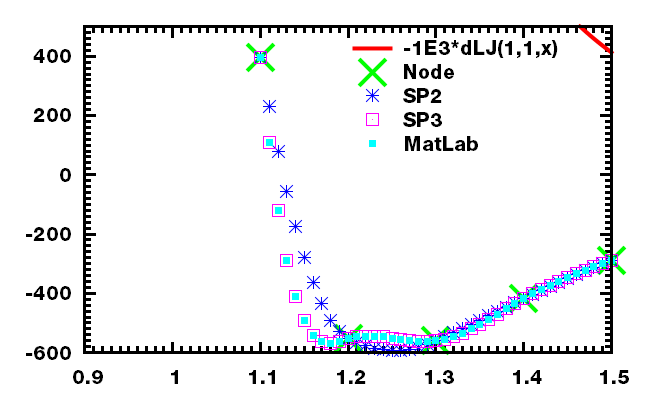
样条函数的积分

对已经拟合的样条函数进行数值积分时可利用可利用Simpson方法. Simpson方法具有三阶精度, 对不超过三次的多项式精确成立, 很适合于二次和三次样条函数.