- 2014年09月23日 16:45:03 初稿
- 2017年02月09日 12:53:30 增加一种新的简单方法
润湿现象的模拟中, 经常需要计算液滴在表面上的接触角. 目前文献上计算接触角的方法主要有三种.
- 利用密度剖面确定边界点, 再拟合成圆, 获得接触角. 非线性拟合
- 利用液滴质心平均高度计算. 求解四次方程
- 利用液滴的体积, 接触面积计算. 求解三次方程
第一种方法计算起来很繁琐, 且牵涉到非线性拟合, 出问题的可能性很大. 后两种方法理论上是一致的, 但方法3比方法2更通用, 适用于任何形状的液滴. 所以我基于方法3实现了接触角的计算.
最近, 我们在论文中提出了一种利用密度分布计算接触角的方法. 这种方法比上面三种方法都简单. 详细说明请参考我们的论文:
Jicun Li, Feng Wang; J. Chem. Phys. 146(5):054702, 2017; 10.1063/1.4974921; Water graphene contact surface investigated by pairwise potentials from force-matching PAW-PBE with dispersion correction.
定义接触角
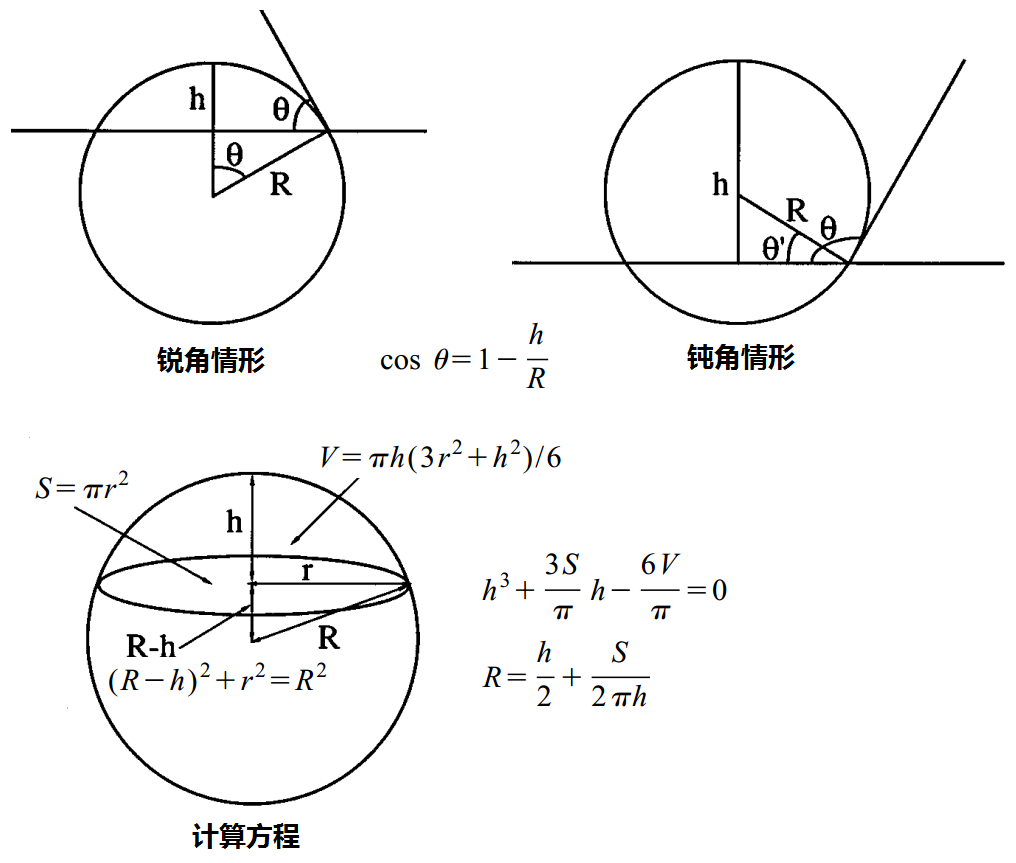
如上图, 无论接触角是锐角还是钝角, 都满足方程
$\cos\q=1-{h \over R}$
根据球冠的体积公式和其他几何关系,
$\alg
S &=\p r^2
V &={1 \over 6} \p h(h^2+3r^2) = {1\over6}\p h^3+{1\over2}\p hr^2={1\over6}\p h^3+{1\over2}hS
\ealg$
可得到球冠高度 $h$, 体积 $V$ 和接触面积 $S$ 满足方程
$h^3+{3S \over \p}h - {6V \over \p}=0$
此方程为特殊形式的三次方程, 根据三次方程的求解公式, 可知存在唯一实数解
$h=t-{S \over \p t}, t=\sqrt[3]{ {3V \over \p}+\sqrt{ {9V^2 \over \p^2}+{S^3 \over \p^3} } }$
求得 $h$ 之后, 计算接触半径 $R={1 \over 2}(h+{S \over \p h})$, 接触角
$\q=\arccos(1-h/R)$
液滴体积与接触面积的计算
方法的关键在于液滴体积与接触面积的计算. 这两个量在计算时都采用格点法. 将整个空间划分成的格点, 统计被占据的格点数, 互相接触的格点数, 分布乘以每个格点的体积与面积, 即可得到体积与面积. 值得注意的是, 液滴的体积由两部分组成, 一部分是被原子占据的体积, 一部分是被原子包围起来的体积. 另外, 此方法假定接触面是平面. 当接触面有起伏时, 面积的计算要更加复杂一些.
一个例子
下面是石墨烯平面上水团簇的构型,
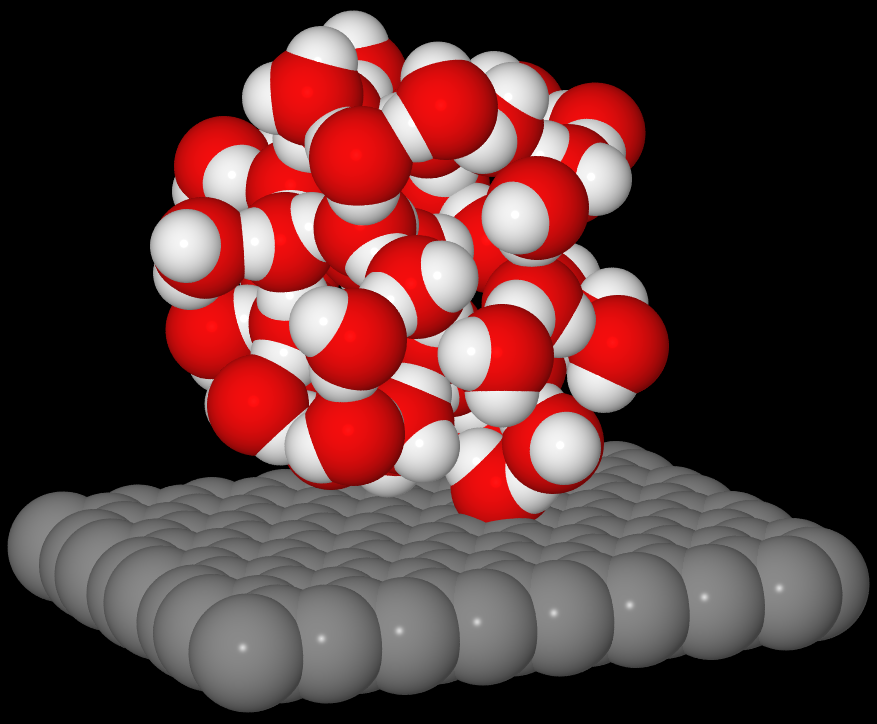
计算结果
#Step Area Area@Plane Vol.Occ Vol.Inter Vol ContAng ContAng@Plane
1 5.876954 5.310000 834.160000 103.992000 938.152000 166.986371 167.640077
参考文献
- T. Werder, J. H. Walther, R. L. Jaffe, T. Halicioglu, P. Koumoutsakos. “On the Water Carbon Interaction for Use in Molecular Dynamics Simulations of Graphite and Carbon Nanotubes”, J. Phys. Chem. B, 2003, 107, 1345-1352
- Joseph Hautman, Michael L. Klein. “Microscopic Wetting Phenomena”, Phys. Rev. Lett., 67(13), 1991
- Cun Feng Fan, Tahir Cagin. “Wetting of crystalline polymer surfaces: A molecular dynamics simulation”, J. Chem. Phys., 103 (20), 1995
评论
-
2017-05-10 09:52:50
momabow请问这个是程序计算吗?有源代码可以分享不 -
2017-05-10 21:56:09
Jerkwin建议你先试试密度剖面的方法, 这个方法不需要自己编程, 只要做拟合就可以了.
