【译】More Is Different 多即不同

2015-03-17 15:07:10

【按】有人说, 还原论并不是科学的全部, “the reduction of cognition to neuro-science”就如”the reduction of chemistry to physics”一样地不合理和不可行. 也有人说, 不合理的一个原因可能是因为还原到更普遍的表示会损失当前特定问题的结构, 即便可行也不高效.

很显然, 此类的说法可以推广到很多学科. 我一直认为科学也是存在不同层次性的, 不同层次之间都有着自己的特点与方法, 互相不可替代. 所以那些关于哪个学科更基础的争论没有必要, 也不会得出什么好的结果. 下面的文章就是关于这个问题的论述.

More Is Different 多即不同

本文原名为: “More Is Different: Broken Symmetry and the Nature of the Hierarchical Structure of Science”, Science, 177(4047): 393-396, 1972.

作者: 安德森(Philip W. Anderson, 1923-), 因”对磁性和无序体系电子结构的基础性理论研究”获1977年诺贝尔物理学奖.

翻译: 郝刘祥

还原论的假设在哲学家中间可能仍然是一个富有争议的主题, 但在绝大多数一线科学家中间, 我想人们肯定都接受了. 我们的心灵, 我们的身体, 以及所有有机物和无机物的运行机制, 就我们所知而言, 都被认为受同一组基本定律所支配. 对于这一组基本定律, 我们相信, 除了某些极端情形之外, 我们已经有了很好的理解.

若是不假思索, 人们往往会把下述命题看成是还原论的一个显而易见的推论: 如果一切事物皆遵守同样的基本定律, 那么只有那些研究真正是基础的东西的科学家才是探索这些定律的人. 这实际上就等于说, 他们不外是一些天体物理学家, 一些基本粒子物理学家, 一些逻辑学家和数学家等. 这种观点, 也是本文所反对的观点, 在韦斯科夫(V. F. Weisskopf)的很有名的一段话中表述得最为清晰¹:

纵观20世纪科学的发展, 人们可以看到两种潮流, 鉴于缺乏更好的术语, 我姑且称之为”内涵性(intensive)研究”和”外延性(extensive)研究”. 简言之: 内涵性研究探求基本定律, 而外延性研究致力于按照已知的基本定律来解释现象. 当然, 这种区分并非没有含混之处, 但就大多数情形而言还是很清晰的. 固体物理学, 等离子体物理学, 或许还包括生物学, 都属于外延性研究. 高能物理学, 以及核物理学中相当的一部分, 都属于内涵性研究. 相比于外延性研究, 内涵性研究总是要少得多. 新的基本定律一旦被发现, 将其应用到迄今尚未解释的现象上来的研究活动便会蜂拥而至. 因此, 基础研究有两个维度. 科学前沿边界甚长, 从最新的内涵性研究, 到刚刚从近期内涵性研究中催生出来的外延性研究, 一直延伸到基于过去数十年内涵性研究的广阔而丰富的外延性研究.

这段话的影响力, 或许可以从这一事实看出: 我听说, 材料科学领域的一位领袖人物近期曾引用这段话, 以敦促那些讨论”凝聚态物理学中的基本问题”的与会者承认, 该领域几乎没有甚至根本就没有这样的问题, 凝聚态物理学不过是外延性科学而已, 而外延性科学, 在他看来与机械工程差别不大.

这种思维的主要错误在于, 还原论假设绝没有蕴含”建构论”(constructionist)假设: 将万物还原为简单基本定律的能力, 并不蕴含从这些定律出发重建整个宇宙的能力. 事实上, 基本粒子物理学家关于基本定律的性质告知我们的越多, 它们对于我们理解科学其余领域中的真正问题越不相关, 对于解决社会问题就更不相关了.

一旦面对尺度和复杂性的双重困难, 建构论假设自然会站不住脚. 大型和复杂的基本粒子集合体的行为, 并不能按照少数基本粒子性质的简单外推来理解. 事实上, 在复杂性的每一个层次, 都会有崭新的性质出现. 在我看来, 为理解这些新行为所进行的研究, 本质上是同样基础性的. 因此, 在我看来, 人们可以按下述设想将科学排列成一个大致为线性的层级: 科学X的基本实体服从科学Y的定律.

X                    Y
固态或多体物理学　　基本粒子物理学
化学　　　　　　　　多体物理学
分子生物学　　　　　化学
细胞生物学　　　　　分子生物学
……　　　　　　　　　……
……　　　　　　　　　……
……　　　　　　　　　……
心理学　　　　　　　生理学
社会科学　　　　　　心理学

但这个层级结构并不意味着, 科学X”仅仅是应用Y”. 在每一个层级上, 新的定律, 概念和原理都是必不可少的, 其所需要的想象力与创造力丝毫不亚于前一个层级. 心理学不是应用生物学, 生物学也不是应用化学.

我本人所从事的多体物理领域或许比其他学科更接近于基础性的内涵性研究. 在该领域, 由于出现了非平凡的复杂性, 我们已着手建立一种一般性的理论, 以说明从量变到质变的转变是如何发生的. 该理论即所谓的”破缺对称”理论, 它或许有助于表明, 还原论的逆命题——建构论——是完全不能成立的. 我将对此作一些基本的, 不完整的解释, 然后就其他层级上的类似情形和类似现象作些更一般的推测评论.

在此之前, 我想澄清两个可能的误解. 首先, 当我说尺度变化引起根本性的变化时, 我的意思并不是指那个人们熟知的观念, 即新尺度上的现象可能服从根本不同的基本定律, 比如, 宇宙学尺度上需要用广义相对论, 原子尺度上则要用量子力学. 我想应该承认, 所有普通物质都服从电动力学和量子力学, 我的讨论也主要限于普通物质(我前面说过, 我们都必须从还原论出发, 对此我深信不疑). 误解之二或许源于这样一个事实, 即破缺对称的概念已被基本粒子物理学家借用过去了, 但我要说, 粒子物理学家仅仅是在类比的意义上使用这个概念, 那里是否真有对称破缺, 对我们来讲仍然是一个谜.

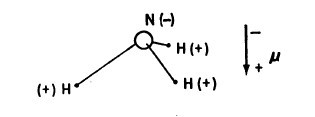
让我们从一个尽可能简单的例子来开始讨论, 那就是氨分子. 我之所以选择它也是因为我在研究生阶段就与它打交道了. 当时人人都熟悉氨, 并用它来校准自己的理论或仪器, 我也不例外. 化学家会告诉你, 氨分子”是”一个由带负电的氮原子和带正电的氢原子构成的三角形的金字塔, 因此它有一个电偶极矩($\m$), 其负向指向金字塔的顶端. 当时这在我看来不可思议, 因为在我所学到的东西中, 没有哪样事物有一个电偶极矩. 教我们核物理的教授的确证明过, 任何核都没有电偶极矩. 鉴于他的论证基于空间和时间的对称性, 该论证就应该是普遍成立的.

不久我就明白了, 事实上该论证是正确的(更准确地说, 是并非不正确), 因为他的表述很谨慎: 任何处于定态的系统(即不随时间而变化的系统)都没有电偶极矩. 如果氨分子的初态是上述非对称态, 那么它不会长时间停留在那个态上. 由于有量子隧道效应, 氮原子会逃逸到氢原子三角形平面的另一侧去, 从而将金字塔颠倒过来; 事实上, 这发生得非常快. 这就是所谓的”反转”, 其频率为 $3 \times 10^{10}$ 每秒. 真正的定态只能是非对称金字塔与其反转的平权叠加. 这个叠加态确实没有电偶极矩(我要提醒读者, 这里是高度简化的说法, 详细内容请查阅教科书).

我不打算在这里给出证明, 但结论是: 一个系统的态, 如果是定态的话, 其对称性必然与支配它的定律相同. 理由很简单: 在量子力学中, 除非为对称性所禁戒, 从一个态转变为另一个态的路径总是存在的. 因此, 如果我们从任意一个非对称态出发, 系统都将跃迁到其他的态, 唯当我们将所有可能的非对称态以对称的方式叠加起来, 我们才能得到定态. 在氨分子的情形, 所涉及的对称性就是宇称——左手性与右手性的等价(基本粒子实验物理学家所发现的特定的宇称破坏与此不相关: 那些效应太微弱了, 影响不到普通的物质).

在看到氨分子没有电偶极矩, 从而满足我们的定理之后, 我们再来看看其他的情形, 特别是那些越来越大的系统, 看看它们的态与对称性是否总是相关. 由更重的原子构成的类似的金字塔形分子是存在的. 磷化氢PH~3~是氨分子的两倍重, 也反转, 但频率仅为氨分子的1/10. 氢原子被重得多的氟原子所取代的三氟化磷分子PF~3~, 在可测的水平上没有观测到反转, 尽管理论上这种反转会在适当的时间间隔内发生.

接下来, 我们可以看看更复杂的分子, 比如由大约40个原子构成的糖分子. 对于这样的分子, 我们不再期待他们会反转. 生命有机体所制造的每个糖分子都是同一螺旋方向的, 但无论是量子隧道效应, 还是常温下的热扰动都不能使之发生反转. 在这里, 我们必须忘掉反转的可能性, 同时抛开宇称的对称性: 对称性定律不是被废除了, 而是已经破缺了.

另一方面, 如果我们用化学方法在热平衡状态附近合成糖分子, 我们将发现, 平均来看, 左手分子与右手分子一样多. 在复杂性不超过自由分子集合体的情形下, 对称性定律总体说来从不会遭到破坏. 我们需要生命物质来产生生命世界中实际的不对称.

在确实很大, 但仍然是无生命的原子集合体中, 可以发生另一种对称破缺, 从而产生净偶极矩或净旋光强度, 或是两者. 许多晶体在每个基本胞腔内都有净偶极矩(热电性), 在有些晶体中, 这个偶极矩可以被磁场反转(铁电性). 这一非对称性是晶体寻求最低能态的自发效应. 当然, 反向偶极矩的态也存在, 并且按对称性有同样的能量, 但系统太大了, 以至于任何热效应或量子力学效应都不能使之在有限时间内(相对于宇宙年龄而言的)从一个态转变为另一个态.

这里至少可以得出三个推论. 其一, 对称性在物理学中极端重要. 所谓对称性, 意指存在不同的视角, 使得无论从哪个视角来看, 系统都是相同的. 说物理学就是关于对称性的研究, 虽有一点夸张, 但也不是那么过分. 牛顿或许第一次展示出了对称性观念的威力, 他可能向自己提出了这样一个问题: 如果我们身边的物质与天空中的物质服从同样的定律会怎样? 也就是说, 如果空间和物质是同质的和各向同性的会怎样?

推论之二是, 即便一块物质的总态是对称的, 它的内部结构也不必是对称的. 我促请你从量子力学的基本定律出发, 预言氨的反转及其易于观测到的性质, 而不是从它的非对称金字塔结构出发一步步推导, 尽管没有任何”态”有那种结构. 有趣的是, 直到20年前², 核物理学家才不再把原子核看成没有任何特征的对称小球, 并认识到, 尽管它绝没有偶极矩, 但也可以变成橄榄球或碟子的形状. 这在核物理学所研究的核反应和激发态光谱中有可观测的后果, 尽管直接证明要比观察氨分子的反转困难得多. 在我看来, 无论是否将此称作内涵性研究, 它本质上都是基本的, 与人们所称的许多基本事物没有两样. 但这并不需要任何新的基本定律的知识, 而且, 试图由这些基本定律一步步将其推导出来是极其困难的, 这不过一种基于日常直觉的灵感, 一下子就把所有东西都理顺了.

这个结果难于推导的基本原因, 对于我们的进一步讨论是富有教益的. 如果核充分小, 就没有办法严格定义其形状: 相互绕转的3个, 4个或10个粒子并不能界定一个转动的”碟子”或”橄榄球”. 仅当核被视为多体系统, 即通常所说的 $N \to \infty$ 的极限时, 这样的行为才是可以严格界定的. 我们对自己说: 一个那种形状的宏观物体会有如此这般的转动和振动激发光谱, 本质上完全不同于一个毫无特征的系统的光谱. 当我们看到这样的光谱——即使分辨率不是很好, 光谱也不是很完整——时, 我们得承认核毕竟不是宏观物体; 它只是趋近于宏观行为. 从基本定律和计算机出发, 欲得出核的这种行为, 我们将不得不做两件不可能的事: 解无穷多个多体的难题, 然后将解得的结果应用到有限系统上.

推论之三是, 一个确实很大的系统的态, 根本不必具有支配该系统之定律的对称性. 事实上, 它通常具有较低的对称性. 突出的例子是晶体: 晶体是按照空间完全齐性的定律, 利用原子和空间来构造的, 却出人意料地展现出一种崭新的, 美妙的对称. 通常, 大系统的对称性要比其背后的结构所暗含的对称性低, 晶体也不例外: 晶体尽管是对称的, 但比起完全的空间齐性, 其对称性要低得多.

或许晶体这个例子过于浅显. 早在19世纪中叶, 晶体的规则性就可以半经验地推导出来, 根本不需要任何复杂的推理. 但有时候, 比如在超导电性的例子中, 新的对称性——所谓破缺的对称性, 因为原初的对称性不再明显了——可能是完全没有料到的, 并且很难形象化. 在超导这个案例中, 物理学家从拥有所有必要的基本定律, 到最终对它作出解释, 花去了整整30年的时间.

超导现象是普通宏观物体发生对称破缺的最突出的例子, 但决不是唯一的例子. 反铁磁体, 铁电体, 液晶和许多其他态的物质都服从一类相当普遍的概念和规则, 不少多体理论家则将其纳入破缺的对称这个一般性的标题之下. 我不想继续讨论历史, 参考文献见注释³.

最基本的观念是, 对于大尺度(即我们自身的宏观尺度)系统, 在所谓 $N \to \infty$ 极限时, 物质将经历尖锐的, 数学上奇异的”相变”, 相变之后不仅微观对称性, 甚至微观运动方程, 都将在某种程度上遭到破坏. 对称性所遗留的痕迹仅表现为一些特征性的行为, 比如长波振动, 这方面我们熟悉的例子是声波; 或超导体的奇异宏观导电现象; 或极为类似的, 晶体点阵以及大多数固体的刚性. 当然, 系统不可能真的违背(violate)——而不是破缺(break)——空时的对称性, 但由于系统各部分发现相互之间某种保持确定的关系从能量角度来考虑更为有利, 因此对称性仅允许物体作为一个整体来应对外力.

这就导致”刚性”(rigidity)概念. 这个概念也适合用来描述超导和超流, 尽管它们表观上呈现出”流体”行为(关于超导, 伦敦[F. London]早就认识到这一点⁴). 事实上, 假设有一种气态的智慧生物, 生活在木星上或银河系中心某处的氢原子云中, 那么普通晶体的性质将比超流氦的行为更令他们感到困惑.

我并不想给大家一个印象, 以为一切都解决了. 比如我认为, 玻璃或非晶相仍然存在迷人的原理性问题, 那里或可揭示出更复杂的行为模式. 尽管如此, 破缺对称对于惰性宏观物体的性质所起的作用, 我们现在已经理解了, 至少原则上已经理解了. 在此我们看到, 整体不仅大于部分之和, 而且迥异于部分之和.

作为上述问题的逻辑延伸, 下一个问题自然是问, 空时基本对称性的更彻底的破坏是否可能, 以及, 如果可能, 会不会出现本质上不同于”简单”相变(即凝聚到更低对称性的态)的新现象?

我们已经排除了液体, 气体和玻璃的表观非对称性(事实上, 它们比人们想象的要对称得多). 在我看来, 下一步是考察那种规则的, 但包含信息的系统. 一方面, 它在空间中是规则的, 从而我们能够将其”读出”; 另一方面, 它的相邻”单元”含有不同的元素. 明显的例子是DNA; 在日常生活中, 一行文字或一段电影胶片有着同样的结构. 这种”载有信息的晶状性”看来对于生命是至关重要的. 生命的发展是否需要进一步的对称破缺, 根本还不清楚.

要是继续探讨生命中发生的对称破缺, 我想至少还有一个现象是可以确认的, 并且是普遍或相当普遍的, 即时间维度的编序(规则性或周期性). 在许多关于生命过程的理论中, 规则的时间搏动都发挥着重要的作用, 如发育理论, 生长和生长极限理论, 记忆理论. 在生物体中, 时间上的规则性是很容易就能观察到的. 它至少发挥着两种作用. 首先, 从环境中提取能量, 以维护持续的准稳定过程之方法, 大多需要具有时间周期性的装置, 比如振荡器和发生器, 生命过程也不例外. 其二, 时间上的规则性是一种处理信息的手段, 类似于负载信息的空间上的规则性. 人的口语就是一个例子; 另可注意的是, 所有计算机都使用了时间脉冲. 前面提到的那些理论还暗示有第三种作用: 利用时间脉冲的相位关系来处理和控制细胞和有机体的生长与发育⁵.

在某种意义上, 结构——目的论意义上的功能性结构, 而不仅仅是晶体的形态结构——必须视为破缺对称层级结构中的一个台阶, 可能介于晶体性和信息弦之间.

基于层层推测, 我想, 下一个台阶可能是功能的层级化或专门化, 抑或两者. 到了某个程度, 我们必须停止谈论不断降低的对称性, 而要开始称其为不断增加的复杂性. 因此, 随着复杂性的增加, 我们将循着科学的层级结构上升. 我相信, 在每一个层级上, 我们都会遇到迷人的, 非常基本的问题, 即: 将不那么复杂的部分组合为一个更为复杂的系统, 并理解由此而来的本质上新型的行为.

多体理论和化学中出现复杂性的方式, 与文化理论和生物学中出现复杂性的方式是不能相提并论的, 除非你泛泛地说, 系统与其部分之间的关系是一个单向通道. 综合几乎是不可能的; 另一方面, 分析不仅是可能的, 而且在各个方面都是卓有成效的: 如果没有理解超导中的破缺对称, 约瑟夫森(B. D. Josephson)或许就不会发现以他的名字命名的效应(约瑟夫森效应的另一个名称是”宏观量子干涉现象”: 超导体中电子的, 或超流液氦中氦原子的宏观波函数之间的干涉效应. 这些现象极大地扩展了电磁测量的精度, 在其各种可能的应用中, 可以预期它将在未来的计算机中发挥重要作用, 最终或许会带来这十年的某些重大技术成就⁶). 卓有成效的另一个例子是, 将遗传学还原为生物化学和生物物理学, 整体上改写了生物学的面貌, 这将带来难以估量的重大后果. 因此, 近期一篇文章⁷所主张的观点——我们都应当”耕耘自己的谷地, 而不要试图在不同学科之间修建跨越山脉的道路” ——是不对的. 事实上, 我们应该认识到, 这样的道路, 特别是通往相邻学科的捷径, 仅仅从一个学科的视角是看不出来的.

粒子物理学家的傲慢以及他们的内涵性研究或许是我们的依靠(正电子的发现者说: “剩下的都是化学了”), 但我们必须摆脱一些分子生物学家的傲慢, 那些分子生物学家力图将人体组织或机能完全还原为化学, 从普通的感冒和各种精神疾病一直到宗教本能. 人类行为学与DNA之间的组织层次, 显然要比DNA与量子电动力学之间的层次要多, 并且, 每个层次皆要求全新的概念构架.

在文章结尾, 我借用经济学中的两个例子, 来说明我想传达的观点. 马克思(Marx)说, 量变会引起质变; 不过, 20世纪20年代巴黎的一场对话总结得更清楚:

菲兹杰拉德(Fitzgerald): 富人不同于我们.

海明威(Hemingway): 是的, 他们有更多的钱.

原文

参考文献