- 2015-04-13 20:59:31 初稿
- 2018-01-21 18:48:01 扩展应用, 增加点阵坐标
- 2019-07-09 19:26:28 补充说明MoS2的创建方法
看到一篇老的文献Helical and rotational symmetries of nanoscale graphitic tubules, PRB, 1993, 47, 5485, 介绍了纳米管的构建方法, 就研究了一下, 弄明白了, 记在这里, 顺便写了个在线的小工具, 方便使用.
如果你在使用过程中发现问题, 欢迎告知.
理论基础
碳纳米管可由石墨烯沿某一方向卷曲而成, 卷曲方向可以利用石墨烯六角形中心来定义, 如下图
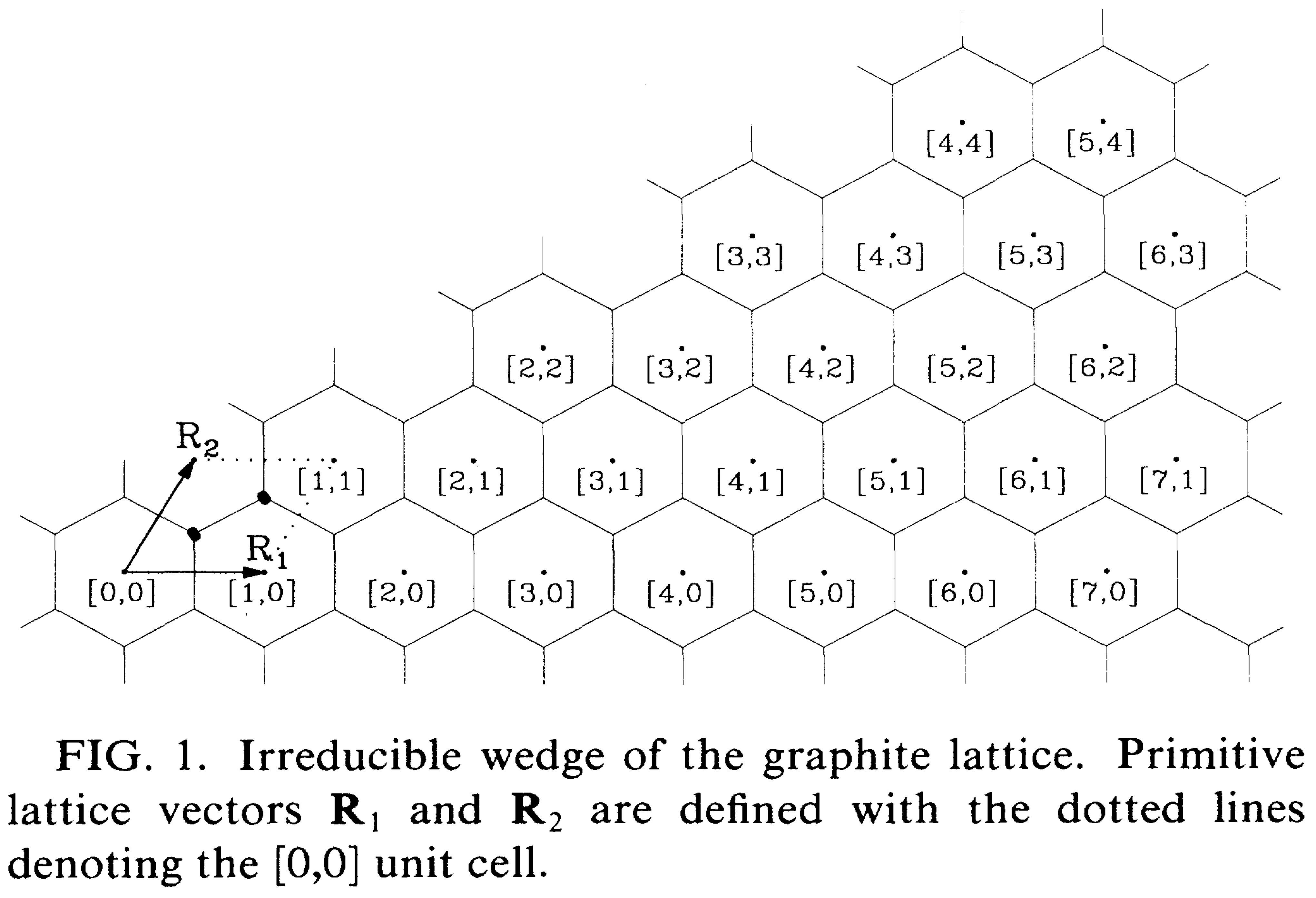
两个平面晶格矢量为 $\vec R_1$ 和 $\vec R_2$, 设卷曲矢量为 $\vec R=m \vec R_1+n \vec R_2$, 为简单起见, 设 $m > n$, 这样每种卷成的纳米管类型都可以利用 $(m,n)$ 来表征, 这称为纳米管的指标.
设六边形的边长, 即碳碳之间的键长为 $a$, 则两个晶格矢量和卷曲矢量分别为:
\[\alg \vec R_1 &=(\sqrt 3 a, 0), &|\vec R_1|&=\sqrt 3 a \\ \vec R_2 &=({\sqrt 3 a \over 2}, {3a \over 2}), &|\vec R_2|&=\sqrt 3 a = \abs{\vec R_1} \\ \vec R &=m \vec R_1+n \vec R_2=({2m+n\over 2}\sqrt 3 a, {3n a \over 2}), &|\vec R| &=\sqrt{3(m^2+n^2+mn)}a \\ \ealg\]由此可得到纳米管的半径
\[r={|\vec R| \over 2\p}={\sqrt{3(m^2+n^2+mn)}a \over 2\p}\]两个碳原子对应的矢量分别为 $\vec d$ 与 $2\vec d$, 其中
\[\vec d={1\over3}(\vec R_1+\vec R_2)=({\sqrt 3 a \over 2}, {a \over 2}), \abs{\vec d}=a\]为方便后面的计算, 这里给出任意两个卷曲矢量的点积与矢量积
\[\alg \vec R &=(m,n) \\ \vec v &=(x,y) \\ \vec R \cdot \vec v &=m x |\vec R_1|^2+ny|\vec R_2|^2+(my+nx) \vec R_1 \cdot \vec R_2 =3a^2[(m+{n\over2})x+(n+{m\over2})y] \\ \abs{\vec R \times \vec v} &= (my-nx) |\vec R_1 \times \vec R_2| ={3\sqrt 3\over2}a^2(my-nx)\\ \ealg\]卷曲后, 第一个碳原子的位置可随意设置, 第二个碳原子相对第一个碳原子的旋转角度为
\[\f={2\p(\vec d \cdot \vec R) \over |\vec R|^2}= {m+n \over m^2+n^2+mn}\p\]这可看作是将 $\vec d$ 在平行于 $\vec R$ 方向的长度, 长度即决定了卷曲后的旋转角度.
第二个碳原子相对第一个碳原子的平移量为
\[\D h={|\vec d \times \vec R| \over |\vec R|}={m-n \over 2\sqrt{m^2+n^2+mn} }a\]这可看作是 $\vec d$ 在垂直于 $\vec R$ 方向上的长度.
纳米管的最高旋转轴为 $C_N$, 其中 $N$ 为 $m$ 和 $n$ 的最大公约数.
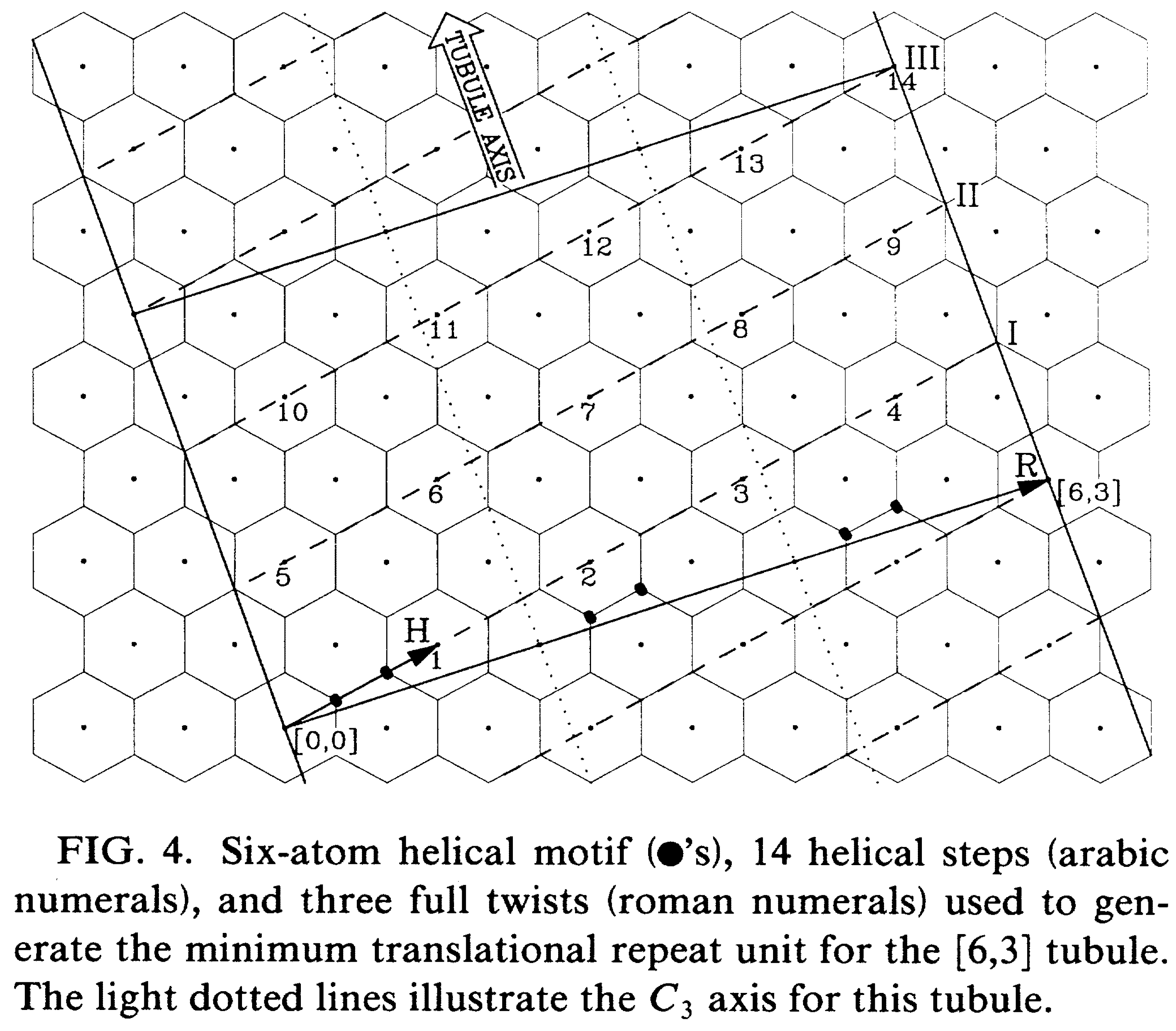
卷成纳米管后, 除具有 $C_N$ 旋转对称性外, 还具有螺旋轴, 此螺旋轴的确定可以利用面积相等法. 首先存在一个矢量 $\vec H=(p,q)$ 满足
\[|\vec H \times \vec R|=N|\vec R_1 \times \vec R_2|\]由此, 可得到下面的关系式
\[qm-pn=\pm N\]由于我们前面已经假定 $m \ge n \ge 0$, 所以上式取正号, 且 $p \ge 0$, 这样就可以确定出 $p,q$ 的值, 由此得到螺旋轴的旋进角和螺距
\[\alg h &= {|\vec H \times \vec R| \over |\vec R|} = {3N \over 2\sqrt{m^2+n^2+mn} } a\\ \a &= {2\p (\vec H \cdot \vec R|) \over |\vec R|} = {p(2m+n)+q(m+2n) \over m^2+n^2+mn } \p \ealg\]注意到, $h$ 与 $\vec H$ 的选取无关,
\[h={|\vec H \times \vec R| \over |\vec R|} = N {|\vec R_1 \times \vec R_2| \over |\vec R|}\]要达到整个周期, 此螺旋轴需要旋转的次数需满足
\[2 k \p = N_{\text{rot} } N \a\]其中 $k$ 为正整数.
这样我们就得到了所有需要的量了.
纳米管基本单元的高度 \(H=N_\text{rot} h\)
其中的原子数 \(2 N N_\text{rot}\)
更长的纳米管只需要沿z轴周期性平移即可.
说明:
- 此方法稍嫌复杂, 直觉上应该还有其他更简单的方法.
- 此方法可推广, 用以构建其他平面周期性结构卷成的纳米管, 如三角形, 四边形等.
- 晶体学上使用的螺旋轴, 其标准螺旋为右旋, 即顺时针旋转, 不同于平面角的方向逆时针旋转.
下面是(6, 3)碳纳米管构建的示意图即结构图, 用于对比
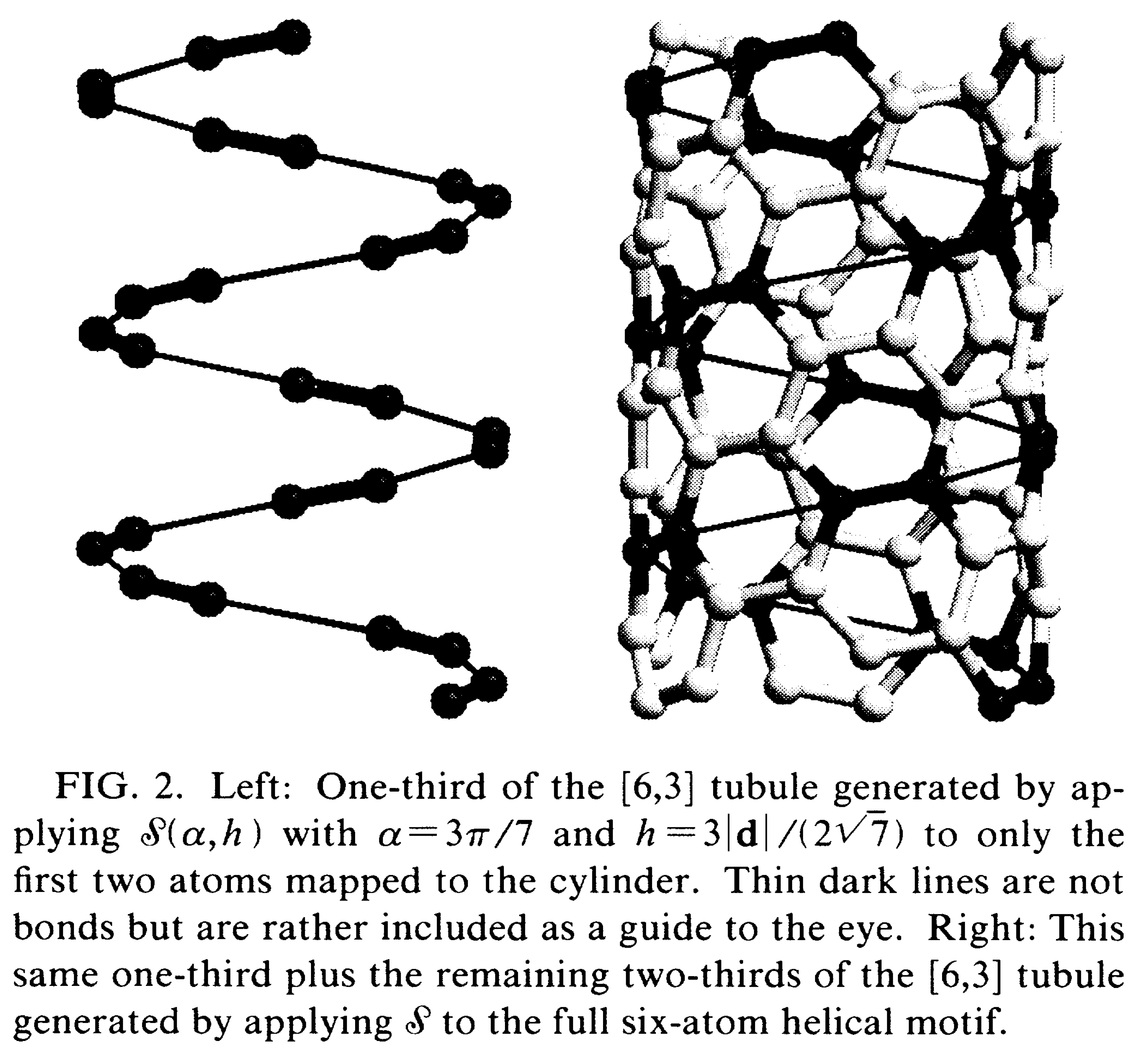
扩展应用
为了能将此方法用于构建其他纳米管体系, 如C-N纳米管, MoS2纳米管, 可以将原先的C原子替换为其他任意的一组原子, 只要二者采用的同样的坐标系坐标即可.
对C-N纳米管, 只要将其中一个点阵碳原子改为氮原子就可以了, 因为基本结构是一样的.
对MoS2纳米管, 有点复杂. MoS2晶体具有层状结构, 每层中原子都处于平面六边形的顶点上, 但z方向的高度不同.
MoS2的晶格参数a=3.160 Å(即Mo-Mo键长), 2z=3.172 Å(z方向S-S距离), 由此, 可以得到六边形边长为 a/sqrt(3)=3.16/sqrt(3)=1.8244 Å, 以Mo原子为基准(0, 0, 0)时, 两个S原子的相对坐标为(0, 0, z), (0, 0, -z). 故此, 两个点阵点为
Mo 0 0 0
以及
S 0 0 -1.586
S 0 0 1.586
参考
- Th. Böker, R. Severin, A. Müller, …, A. Mazur, J. Pollmann; Phys. Rev. B 64(23):235305, 2001; 10.1103/PhysRevB.64.235305
- N. Zibouche, A. Kuc, T. Heine; Eur. Phys. J. B 85(1):49, 2012; 10.1140/epjb/e2011-20442-1
- Jin Xiao, Mengqiu Long, Xinmei Li, …, Han Huang, Yongli Gao; Sci Rep 4(1):4327, 2014; 10.1038/srep04327
- Gotthard Seifert, Humberto Terrones, Mauricio Terrones, Gerd Jungnickel, Thomas Frauenheim; Phys. Rev. Lett. 85(1):146-149, 2000; 10.1103/physrevlett.85.146
纳米管在线创建工具
类型指标:m n
基本单元数: 六边形边长/C-C键长(Å):
径向位置随机(Å):X方向: Y方向:
|
第一点阵点原子坐标 |
第二点阵点原子坐标 |
纳米管半径(Å): 纳米管高度(Å): 纳米管总原子数:
基本单元高度(Å): 基本单元原子数:
第二原子偏移(Å): 第二原子转角(π):
螺旋轴螺距(Å): 螺旋轴旋进角(π): 旋转次数:
(m, n): (p, q): gcd(m, n): qm-pn:
|
XYZ文件 |
</td> </tr></table> |
