2015-11-20 17:11:25
问题
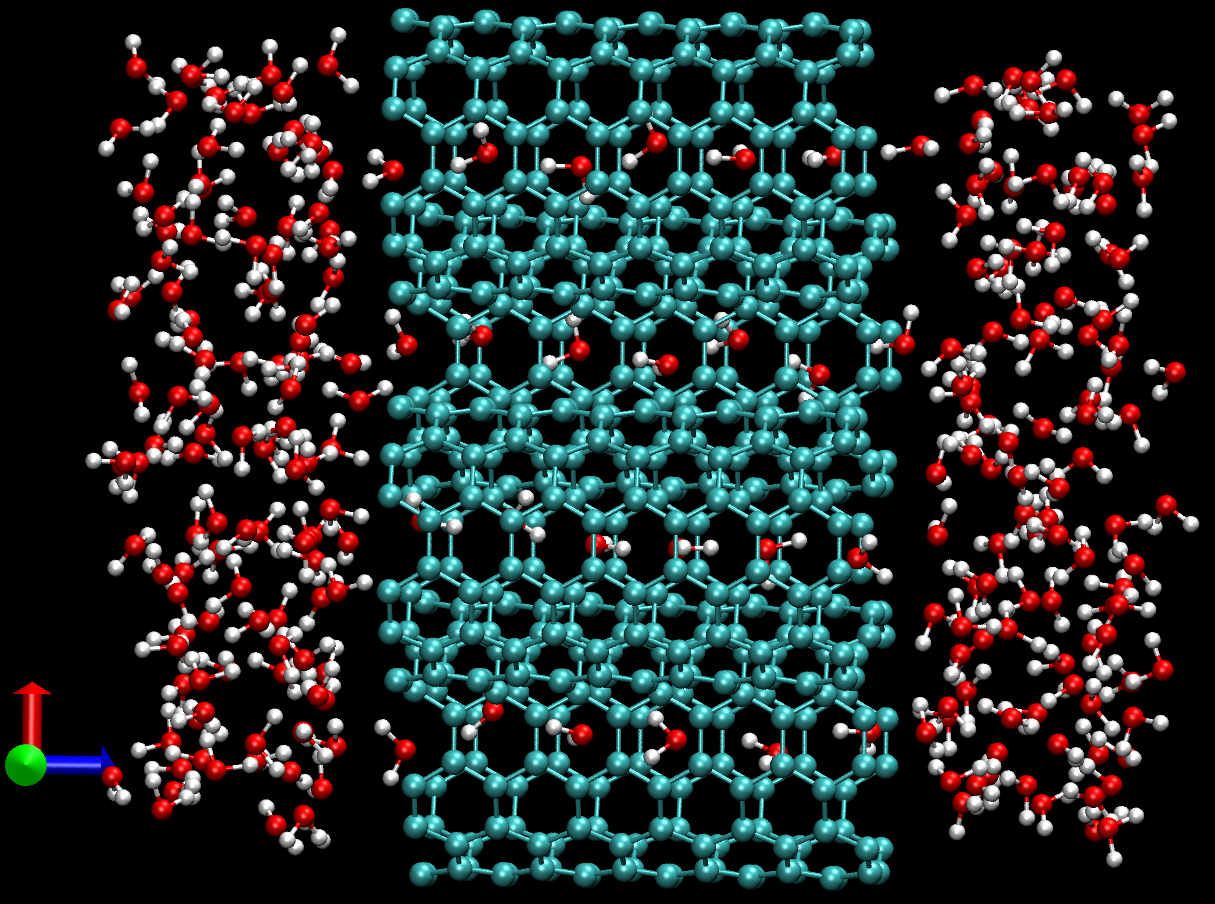
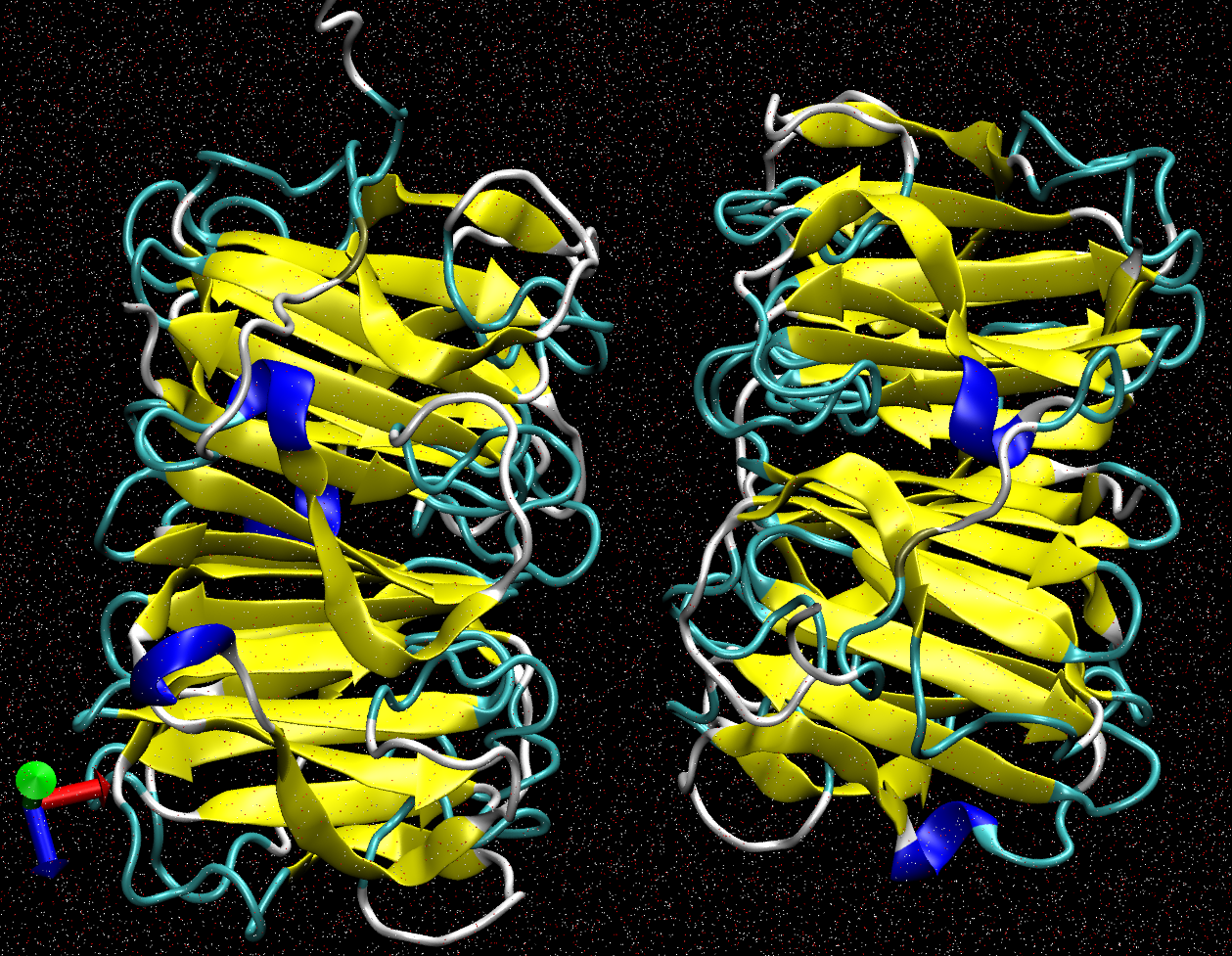
分子动力学模拟得到轨迹后, 如何统计一定区域内溶剂分子的个数? 例如, 蛋白质某个通道或某个空腔内水分子的个数.
解答
这个问题在生物模拟中常见, 在一些材料模拟中也会遇到, 但由于计算不易, 所以进行这种分析的文章不多见. 下面是我想到的做法, 记在这里供大家参考.
首要问题就是, 如何确定需要进行统计的区域. 对于简单的情况, 如碳纳米管, 很容易定义区域内部和区域外部. 但对于复杂的情况, 定义区域及其内部和外部首先就是一个问题. 参照数学上的做法, 对于可定向的区域, 无论其如何复杂, 总可以将其近似划分为一些小的凸包(convex hull), 我们只要解决凸包内的统计问题就可以了. 这样问题的难度就降低了一些.
采用凸包近似后, 接下来要解决的问题是如何根据区域内的粒子坐标得到此区域对应的凸包. 这是计算几何中的一个经典问题, 有多种算法, 复杂程度各不相同, 许多软件中也有相应的实现函数, 如果不是自己写代码的话, 只要知道如何调用这些函数就可以了. 如果是自己写代码, O(N^2)的算法很容易实现, 但要实现O(nLnN)的算法并不简单. 下面是一些有参考价值的网页:
- How to find convex hull in a 3 dimensional space
- C代码 A program for convex hulls
- C++代码 3dhull
- FORTRAN代码 Three-Dimensional Convex Hulls
- qhull程序 用 qhull 计算三维点集的凸包
- CGAL计算几何库 CGAL
确定了凸包之后, 最后的问题就是如何判断给定的点是在凸包内部还是外部. 这也是计算几何中的一个典型问题, 有固定的解法. 如果只需要判定一个点是否处于一组点构成的凸包内部, 不必构造出凸包, 只要利用凸包内部的点满足的线性规划条件就可以了. 但如果需要对多个点进行判定, 那么先构造出凸包, 再进行判断, 效率会高很多. 这种情况下, 也有多种方法, 如四面体剖分法, 体积法等, 但最高效的方法应该是利用凸包各个面的法线与待判定点连接面内点形成向量的点积来判断. 如果点处于凸包内部, 那么所有点积的乘积大于零, 否则的话小于零. 有关讨论可参考下面的网页:
- how can I identify points are inside convex hull in Matlab separately
- Detect a point inside a convex hull in high dimension
- MatLab 程序 Inhull
上面这种构造凸包的方法在数学上很严格, 也可以处理任意的形状, 只要确定了区域的点即可. 但实现起来需要编程, 具有一定的难度. 为此, 根据不同的情况, 我们可以采用其他近似方法. 需要注意的是, 这些方法虽然可行, 但只适用于一些特定的情况, 所以在使用前需要检查适用条件是否满足.
如何区域具有规则的几何形状, 并且在模拟过程中近似不变, 这样可以容易地写出区域内部点满足的条件. 在这种情况下只要知道要判断的坐标, 根据几何条件就很容易判定并统计了.
即便模拟过程中确定几何区域的点会发生变化, 但仍可以利用其来确定内部点满足的几何条件, 这种情况下只要能写出这些几何条件就可以判定了.
具体到实现, 可自己写代码, 也可以使用不同的程序, 如VMD或是GROMACS的select模块. 但在进行统计前, 建议先对轨迹进行周期性边界条件的处理, 将区域中心置于原点或盒子中心, 这样给出的判定条件可能更简单. 还有就是可以提前对要判定的点进行粗略的筛选, 去掉那些明显不会处于区域内部的点, 这样再处理时会更快.
