扩散模式的分类以及扩散系数的计算|Jerkwin

2017年05月02日 19:58:51

看到一篇科技论文的报道纳米粒子反常受限扩散研究获得进展, 是有关扩散的, 就顺便整理一下与扩散有关的理论知识, 这些知识在利用分子动力学模拟研究扩散现象时可能会用得上.

扩散模式的不同分类

使用MD计算粒子的扩散系数时, 一般都是基于粒子进行布朗运动, 遵循简单的扩散模型. 实际上, 根据外界限制条件的不同, 粒子的扩散有多种模式, 不同扩散模式下粒子的均方位移MSD(mean square displacement)与时间t的关系很不一样. 根据MSD的表现, 我们可以推测出扩散的不同机理. 研究粒子, 如量子点在细胞中的运动时, 人们总结了粒子几种可能的扩散模式. 下面是论文Confined Lateral Diffusion Of Membrane Receptors As Studied By Single Particle Tracking (Nanovid Microscopy). Effects Of Calcium-induced Differentiation In Cultured Epithelial Cells中给出的总结.

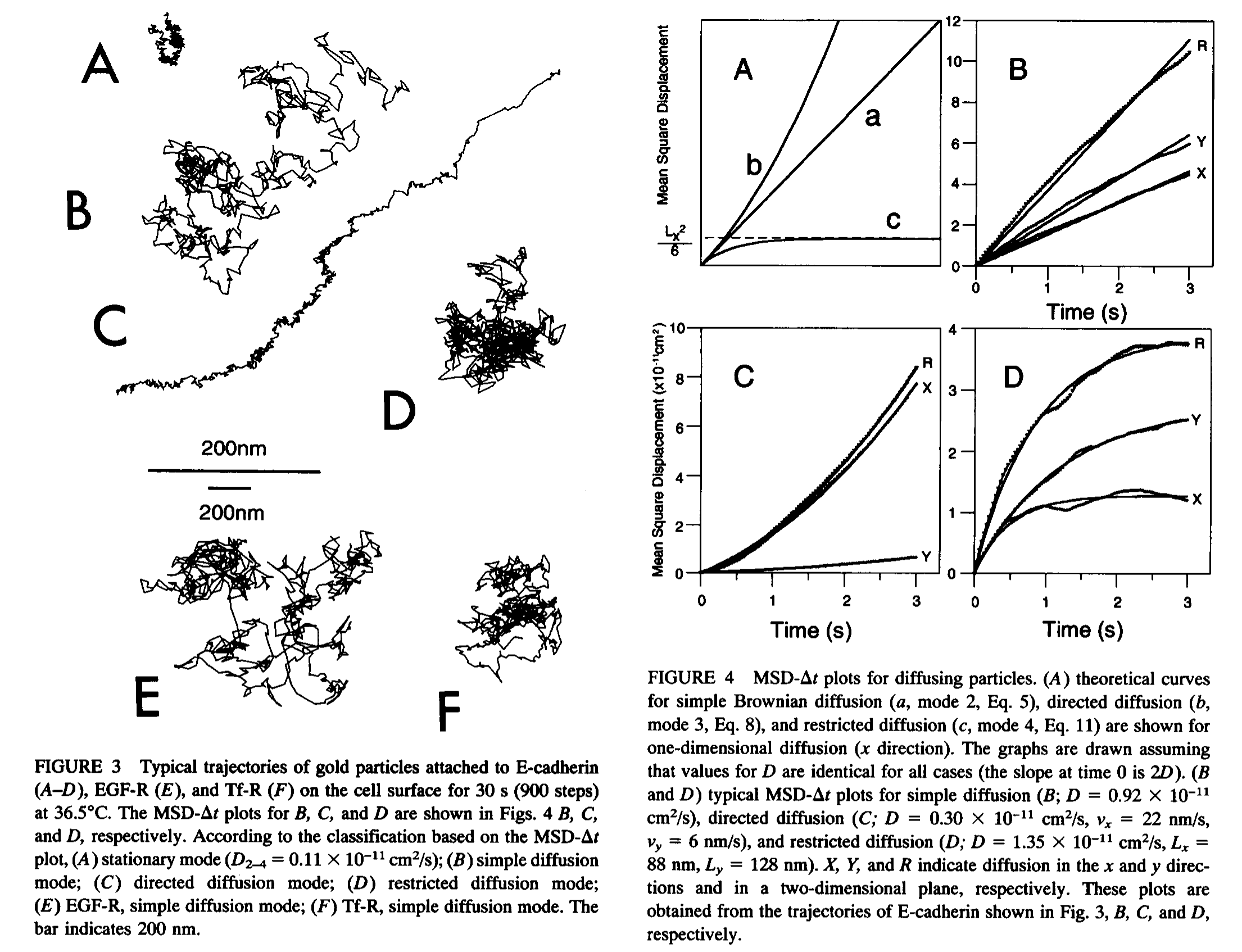
静态模式 Stationary mode

粒子基本不运动, 扩散系数接近零.
简单(或布朗)扩散模式 Simple diffusion mode

粒子做简单的布朗扩散运动

$\text{MSD}(\D t)=nD \D t$, $n$ 为粒子运动空间的维数
定向扩散(或传输)模式 Directed diffusion mode (transport mode)

粒子在做随机扩散的同时沿某一方向以恒定的速度漂移

$\text{MSD}(\D t)=nD \D t+v^2 \D t^2$
限制扩散模式 Restricted diffusion mode

粒子在做布朗扩散时, 其运动空间被限制在某一范围内, $0 \le x \le L_x$, $0 \le y \le L_y$, $0 \le z \le Lz$. 粒子的运动等价于在无限深方势阱中的布朗扩散. 细分起来又可分为两类: 受限模式confinement model和系索模式tethering model. 但仅根据轨迹无法区分这两种模式.

$\alg \left< x^2 \right>(t) &={L_x^2 \over 6}-{16 L_x^2 \over \p^4} \Sum_{n=1(odd)}^\infty {1 \over n^4} \exp\left[ -{1\over2} ({n\p\s_x \over L_x})^2 t \right], &\s_x^2 &=2 D_x \ealg$

$\alg \left< y^2 \right>(t) &={L_y^2 \over 6}-{16 L_y^2 \over \p^4} \Sum_{n=1(odd)}^\infty {1 \over n^4} \exp\left[ -{1\over2} ({n\p\s_y \over L_y})^2 t \right], &\s_y^2&=2 D_y \ealg$

$\alg \left< z^2 \right>(t) &={L_z^2 \over 6}-{16 L_z^2 \over \p^4} \Sum_{n=1(odd)}^\infty {1 \over n^4} \exp\left[ -{1\over2} ({n\p\s_z \over L_z})^2 t \right], &\s_z^2&=2 D_z \ealg$

$\alg 6D &=2D_x+2D_y+2D_z \ealg$
受障模式 Obstacle-impeded diffusion mode

粒子进行自由扩散时受障碍物限制, 障碍物可以是固定的, 或者有一定的移动能力. 在这种情况下, 长程扩散会减弱但仍大于零. 这种模式比较难与限制模式区分开来. 对各向同性的碰撞几率,

$\text{MSD}(\D t)=4 D\D t+A+B\ln (C\D t)$

简单扩散模式对应的扩散系数

大多数情况下MD研究的是简单扩散模式, 在此假定下求扩散系数的步骤是先算MSD, 然后拟合MSD线性部分的斜率, 再除以6(二维体系除以4)就是扩散系数. 但在拟合的时候, 有一个选取拟合数据范围的问题, 也就是确定用哪段时间范围内的MS进行拟合. 很显然, 使用不同时间段的数据, 拟合结果会有所不同. 拟合时不能使用MSD数据的起始部分, 因为起始部分属于扩散弛豫过程, 除非专门研究这个过程, 拟合的初始时间要大于扩散弛豫时间; MSD数据的最后部分也不能用, 因为计算MSD时, 关联时间越大, 数据点越少, MSD的误差越大, 所以拟合时只能取数据中间接近线性的一部分.

如果是普通扩散过程, 在开始的一小段时间内MSD是关联时间的二次函数, 代表无障碍的定向扩散. 随着关联时间的增加, MSD会很快过渡到一次函数阶段, 代表正常扩散. 这个一次函数区域一般来说就是计算扩散系数的最佳区域.

由于关联时间越大, 涨落越大, 所得MSD的误差也越大, 所以拟合的最大关联时间也不是越大越好. 此外, MSD曲线的光滑程度与模拟时间成正比, 一般模拟时间会取最大关联时间的10倍或更大. 也可以多次模拟求平均值.

具体怎么决定拟合的关联时间范围呢? 一种方法是选取不同的最大关联时间, 如1 ps, 5 ps, 10 ps, 50 ps, 100 ps等作出MSD随最大关联时间变化的曲线, 从而确定体系的特征扩散弛豫时间. 更好的方法是计算动扩散系数(RDC, running diffusion constant), 根据它的变化来确定关联时间的拟合范围

\[\text{RDC}(t) = { \rmd{\text{MSD} }(t) \over 6 \rmd t} \approx { \text{MSD}(t) \over 6t}\]

动扩散系数曲线要趋近于水平线才算收敛. 对于普通扩散, 随关联时间的增加, 动扩散系数会从零增加到一个定值. 对于气体, 增加过程一般是单调的; 对于稠密液体, 可能会有局部涨落. 当然，单次模拟数据会有较大涨落, 我们很难通过一次模拟结果就判断出这个定值是多少, 所以需要多次模拟取平均.

具体做法就是, 使用 MSD/6t 对t作图, 这样数据成正比的线性部分应该是一条上下稍有波动的水平线, 很容易看出来. 我们可以简单地将这段时间内扩散系数的平均值模拟的扩散系数, 也可以对此时间段内的数据进行拟合求出扩散系数. 这两种方法得到的扩散系数值应该差不多, 但建议采用后一种方法, 虽然麻烦点, 但标准

这种方法的一种变形是做双对数 log(MSD)-log(t) 图, 选取其斜率尽可能接近1的一段求扩散系数. 这很容易理解

\[\ln \text{MSD}(t) = \ln t+\ln(6D)\]

缺点在于单凭肉眼很难判断数据斜率为1的部分.

更复杂的处理方法, 可以采用随机抽样一致性算法(RANSAC)或者非线性拟合方法来自动确定最佳拟合值, 其大致思想是在指定的条件下, 寻找一条直线, 使得距离直线一定范围内的点数最多. 但这些方法使用麻烦, 所以文献中较少看到.

MD计算设置

系综选用: 大多用NVT, 但NPT也可以, 不过要注意NPT时盒子标度导致的位置变化
MSD计算属于相关函数计算, 需要大量的数据点, 因此, 需要长的模拟时间以及短的输出间隔. 只有模拟时间要足够长才能保证扩散系数收敛.
扩散系数

单位 [D] = nm²/ps = 10^-6 m²/s = 10^-2 cm²/s = 10³ 10^-5 cm²/s = 10³ 10^-9 m²/s

1 cm²/s = 100 nm²/ps

298.2 K时, 水的扩散系数 Dwat=(2.30 &pm; 1.5%) x 10^-9 m²/s=(2.30 &pm; 1.5%) x 10^-5 cm²/s.

其他一些分子的扩散系数, 可查阅CRC物理化学手册.
gmx msd计算时可以设定拟合时间, 计算后会输出相关信息以及扩散系数, 但如果你不能确定拟合时间范围的话, 给出的数值最好不要直接使用.
```
  %# Diffusion constants fitted from time 50 to 100 ps
  % D[         F] = 3.3547 (+/- 0.1417) (1e-5 cm^2/s)
```

附: 反常扩散sub-diffusive

理论上讲, 当时间足够长时, 粒子的运动可以近似看作随机游走, 那么MSD与关联时间成线性关系. 在三维情况下, $\text{MSD}(t) = 6Dt$. 对上式两边取对数作图, 斜率为1. 如果计算MSD的时间不够长, 你会发现MSD与时间呈非线性关系 $\text{MSD}=D_\a t^\a (a \lt 1)$. 这时对两边取对数作图斜率不为1. 这种情况称为sub-diffusive行为. 直观的解释是粒子的游走可以近似看作是在其他粒子形成的”溶剂笼”里活动, 粒子长时间运动的MSD可近似看作粒子在各个溶剂笼间的活动, 因此与时间呈线性关系, 而粒子短时间运动的MSD可看作是粒子还没有走出第一个溶剂笼, 因此是呈非线性的sub-diffusive行为. 为了克服sub-diffusive行为对计算扩散系数带来的影响, 通常是计算足够长时间的MSD, 将MSD/t或d(MSD)/dt对时间作图, 考察MSD斜率随时间的变化, 当斜率达到稳定值时就可以用来计算扩散系数了.

参考资料

樊哲勇, 用分子动力学模拟计算扩散系数