哲●科●文Jerkwin 类别 标签 链接 关于 订阅

AMBER高级教程A17：伞形采样实例--计算丙氨酸二肽Phi/Psi旋转过程的平均力势PMF

类别: 科   标签: amber   阅读次数:   版权: (CC) BY-NC-SA ✕

在本教程, 我们将学习怎样结合Alan Grossfiled的加权直方图分析方法(WHAM)去产生平均力势. 通常我们可能想要知道自由能随特定反应坐标的分布情况. 这种分布被称为平均力势, 它对识别过渡态, 中间产物和终点的相对稳定性是非常有用的, 一开始人们可能认为能够通过运行一次MD模拟来产生自由能随特定反应坐标的变化, 然后查看样品采样的概率. 然而, 通常感兴趣的能量位垒是kbT的数倍, 因此MD模拟将仍然处在它一开始的局部最小值或者跨越不同的最小值, 但极少会采样到过渡态. 采样的缺乏使得我们不能产生一个精确的PMF. 事实上, 甚至对于很小的系统我们也需要超过一毫秒的MD去获得可用的采样. 这显然很难达到, 因此需要使用更好的方法.

其中一种方法是伞形采样. 这项工作可以通过分解反应坐标成为一系列窗口, 然后采用限制迫使反应坐标维持在靠近窗口的中心. 显然对于理想采样, 最好的方法是用自由能形貌自身作为伞形限制. 这将使能量表面足够平坦以至统一采样. 然而这不可行, 因为它需要我们在计算它之前知道能量表面形状. 相反, 我们通常所做的是用一系列简谐势去限制反应坐标到某个值. 这一系列表示采样的反应坐标值的直方图能够被产生, 假设窗口重叠, 这就能够使用加权直方图分析方法去处理结果, 从而去除限制偏置并恢复PMF.

在本教程我们将使用伞形采样去计算丙氨酸三肽顺反异构化过程的PMF.

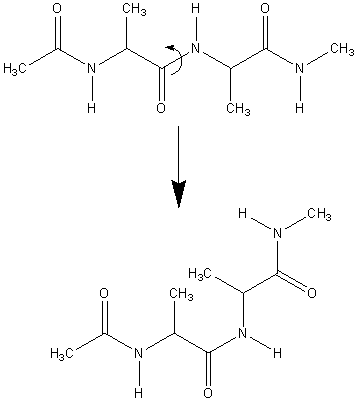
图2

教程包括三部分

第一节: 构建并驰豫初始结构

我们所要做的第一件事是产生初始结构并驰豫它, 以至于我们可以用它作为运行伞形采样的输入. 通常情况下, 会从pdb文件中获得这样的结构. 然而, 在我们这个例子中系统很简单, 我们使用leap命令去构建它(Amber16的tleap需要添加oldff路径)

$AMBERHOME/bin/tleap
source leaprc.ff99SB
mol = sequence { ACE ALA ALA NME }
solvateoct mol TIP3PBOX 10.0
saveamberparm mol ala_tri.prmtop ala_tri.inpcrd

产生文件ala_tri.prmtop, ala_tri.inpcrd

因为这是个小体系, 我们在热浴和驰豫时不需要过于柔和. 我们所要做的是:

  1. 最小化(1000 steps) 01_min.in
  2. 热浴(NVT, 0到300 K, 20 ps) 02_heat.in
  3. 驰豫(NPT, 300 K, 100 ps) 03_equil.in
01_min.in
1
2
3
4
5
6
minimize
 &cntrl
  imin=1, maxcyc=1000, ncyc=500,
  cut=8.0, ntb=1, ntp=0,
  ntc=2, ntf=2,
 /
02_heat.in
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
heat NVT 20ps
 &cntrl
  imin=0, irest=0, ntx=1,
  nstlim=10000, dt=0.002,
  ntc=2, ntf=2, cut=8.0,
  ntt=3, gamma_ln=1.0,
  ntb=1, ntp=0,
  tempi=0.0, temp0=300.0,
  ntpr=100, ntwx=100, ntwr=10000,
  ioutfm=1,
 /
03_equil.in
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
equil NPT 100ps
 &cntrl
  imin=0, irest=1, ntx=5,
  nstlim=50000, dt=0.002,
  ntc=2, ntf=2, cut=8.0,
  ntt=3, gamma_ln=1.0,
  ntb=2, ntp=1, tautp=1.0,
  temp0=300.0,
  ntpr=500, ntwx=500, ntwr=10000,
  ioutfm=1,
 /

现在我们通过pmemd程序运行这些. 在双cpu机器上使用两个处理器运行它们:

mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i 01_min.in -o 01_min.out -p ala_tri.prmtop -c ala_tri.inpcrd -r 01_min.rst
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i 02_heat.in -o 02_heat.out -p ala_tri.prmtop -c 01_min.rst -r 02_heat.rst -x 02_heat.nc
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i 03_equil.in -o 03_equil.out -p ala_tri.prmtop -c 02_heat.rst -r 03_equil.rst -x 03_equil.nc

得到文件01_min.out, 01_min.rst, 02_heat.out, 02_heat.rst, 02_heat.nc, 03_equil.out, 03_equil.rst, 03_equil.nc

你应该检查这些结果, 确保系统保持稳定等等. 你也应该注意到丙氨酸三肽任然处于反式结构. 我们现在能进行下一节, 并建立伞形采样模拟.

第二节: 运行伞形采样计算

既然我们已经驰豫了初始结构, 接下来计算部分是在单个伞形窗口运行MD. 所需窗口数目的选择与所使用的限制大小有点像魔法难以琢磨. 我们遇到的又一个问题是在我们计算之前能否知道解决方案最理想的选择. 关键点在于记住选择的窗口数的终点必须重叠. 例如, 窗口1必须采到窗口2的一部分, 等等. 这本质上意味着我们不能错误的去选择太多的窗口, 除非你想要花费过多计算时长. 力常数同样地也必须足够大以确保我们实际采集到了合适大小的相空间子集, 我们使窗口更窄去防止它们重叠. 通常我们能够根据沿着路径的位置去调整窗口和限制的大小. 例如, 如果观察两个距离非常近, 处于范德华半径内的离子分离, 我们必须采用很强的限制和大量的窗口. 随着距离的增加, 我们能使用越来越弱的限制和间距更大的窗口.

在这个例子中, 我们将改变C-N键的夹角从0到180度. 下面的图显示了二面角, 我们将随prmtop文件中相关原子号去改变它(编号为VMD索引数index+1, 因为VMD索引数从零开始)

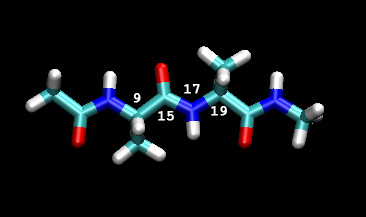
图4

首先, 我们近似地使用间隔为3°的伞形窗口. 这将有61个计算去运行. 我们将使用200 KCal/mol-rad2的力常数, 它大于所期望的势垒高度. 理想情况应该是在10到30 Kcal的范围内, 这样就足以确保我们对整个反应坐标进行采样, 但不能太大, 那样我们结束时的窗口就不能重叠. 在完成初始的计算之后, 我们将检查重叠部分, 然后我们可以返回并通过额外的模拟来弥补不足.

我们在每个窗口所做的模拟量必须能使采样收敛. 因此, 如果我们增加我们运行一个窗口的长度, 生成的采样角直方图不会变形. 理想情况下, 你需要运行初始模拟, 然后计算PMF, 随后丢掉最后20%的数据并再次计算PMF, 看它的变化. 如果它不改变, 那么你的采样就足够了, 如果它变化显著, 那么你可能需要做更多的采样.

首先我们尝试运行每个窗口150 ps, 在这个驰豫过程中丢掉了前50 ps数据. 因此对每个窗口, 从0到180度, 我们需要做:

  1. 最小化(2000 steps, no shake)
  2. 驰豫MD(NPT 50 ps, 1 fs步长)
  3. 数据收集(MPT 100 ps, 1 fs步长)

我们需要克服的一个问题是, 我们只有一个起始结构 (180°). 因为如果我们从180°的结构开始0°模拟, 约束力就会把结构拉开. 更理想的解决方案是先运行180°模拟, 然后以它作为输入再次开始177°的模拟, 然后是174°的模拟等等. 这种方式在计算时强加一系列限制, 使得我们无法使用计算机集群去运行模拟. 因此从180°结构开始(我们前期驰豫后的丙氨酸-三肽的平衡位置. ), 我们将手动运行120°的模拟, 然后从最终120°结构手动运行60°模拟. 这将给我们3个初始结构, 我们可以使用它们作为不同窗口的起始点.

我们将使用在AMBER11手册4.2节描述的AMBER简谐限制, 在《AMBER 11手册》第4.2节中描述. 这里的例子是使用120°最小化后作为输入文件, 驰豫和数据收集:

mdin_min.120 mdin_equi.120 mdin_prod.120

mdin_min.120
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
2000 step minimization for 120 deg
 &cntrl
  imin = 1,
  maxcyc=2000, ncyc = 500,
  ntpr = 100, ntwr = 1000,
  ntf = 1, ntc = 1, cut = 8.0,
  ntb = 1, ntp = 0,
  nmropt = 1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.120
mdin_equi.120
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
50 ps NPT equilibration for 120 deg
 &cntrl
  imin = 0, ntx = 1, irest = 0,
  ntpr = 5000, ntwr = 50000, ntwx = 0,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 50000, dt = 0.001,
  tempi=0.0, temp0 = 300.0, ntt = 3,
  gamma_ln = 1.0,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1, ioutfm=1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.120
mdin_prod.120
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
100 ps NPT production for 120 deg
 &cntrl
  imin = 0, ntx = 5, irest = 1,
  ntpr = 10000, ntwr = 0, ntwx = 10000,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 100000, dt = 0.001,
  temp0 = 300.0, ntt = 3,
  gamma_ln = 1,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1, ioutfm = 1,
 &end
 &wt
  type='DUMPFREQ', istep1=50,
 &end
 &wt
  type='END',
 &end
DISANG=disang.120
DUMPAVE=dihedral_120.dat

这里有几件需要注意的事情. 我没有用shake做最小化. 因为sander/pmemd使用shake不能很好的工作, 它会能量最小化结构但在最小化之前会停止. 通常情况下这不是问题, 但在这里, 由于使用了限制条件和最优的初始结构, 我要更为谨慎. 在两个MD期间, 虽然我开启了shake, 但我仍然使用1 fs步长. 这可能是不必要的, 但谨慎没错. 我还将压力的驰豫时间 (taup) 设置为5 ps, 比默认的1 ps要长. 这也是为了减少可能出现的不稳定问题. 最后注意, 所有文件设置nmropt=1, 参考名为disang.120的文件. 这个文件是我们用来说明简谐限制的:

disang.120
1
2
3
4
5
6
Harmonic restraints for 120 deg
 &rst
  iat=9,15,17,19,
  r1=-60.0, r2=120.0, r3=120.0, r4=300.0,
  rk2=200.0, rk3=200.0,
 /

这里的iat指的是限制的原子序号, 例如9,15,17和19. 然后我们指定r1到r4共4个值来定义力势的形状. r1-r2之间有力常数为rk2的简谐势, r2-r3之间没有, r3-r4之间有力常数为rk3的简谐势. 既然这样, 我们设rk2=rk3和r2=r3, 从而能给我们在120°时施加于具有最小值的简谐势. 简谐势不是必须的, 然而我们在下一节使用WHAM产生PMF, 它假设限制是简谐势, 这正是我们现在所用的.

还需要注意的是, 在成品模拟中我们指定的dump频率为50和一个输出文件dihedral_120.dat. 这意味着力会每50步(50 fs)写入一次到dihedral_120.dat文件中.

我们现在手动运行3个计算去检查是否正确(注意03_equil.rst是最终结构, 是从最开始不限制驰豫后产生的, 即180°)

mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_min.120 -o ala_tri_min_120.out -p ala_tri.prmtop -c 03_equil.rst -r ala_tri_min_120.rst
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_equi.120 -o ala_tri_equil_120.out -p ala_tri.prmtop -c ala_tri_min_120.rst -r ala_tri_equil_120.rst
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_prod.120 -o ala_tri_prod_120.out -p ala_tri.prmtop -c ala_tri_equil_120.rst -r ala_tri_prod_120.rst -x ala_tri_prod_120.nc

产生文件: ala_tri_min_120.out, ala_tri_min_120.rst, ala_tri_equil_120.out, ala_tri_equil_120.rst, ala_tri_prod_120.out, ala_tri_prod_120.rst, ala_tri_prod_120.nc, dihedral_120.dat

你应该检查计算来确保他们是正确的, 关键要检查的是在从180°到120过程中, 限制不会拉断任何东西, 确保限制正常工作. 尤其是应该看一下dihedral_120.dat文件. 我们能画出图形:

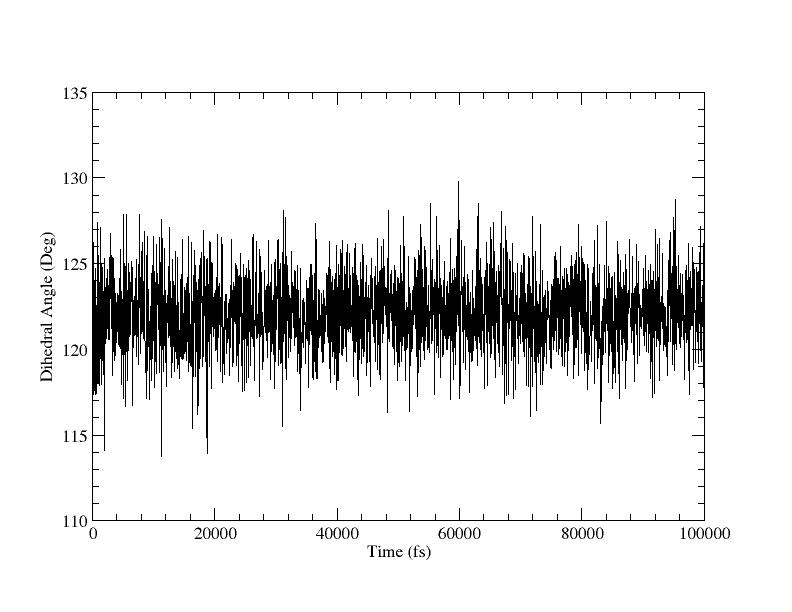
图7

这看上去还可以, 虽然平均值稍微小于120°但可以了, 因为力势本身有一定偏差, 导致远离平衡位置. 这也提醒我们限制力不够大. 我们也能够绘制直方图以便于检查它的宽度:

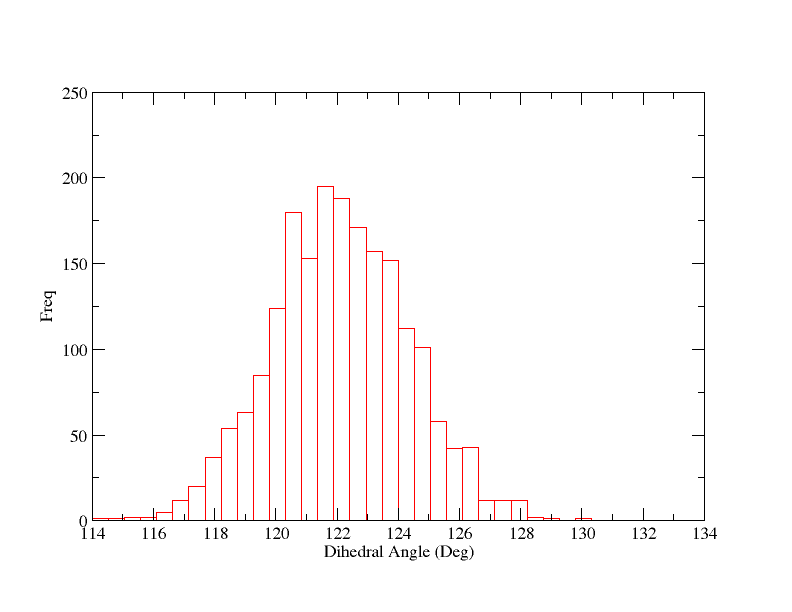
图8

这也告诉我们限制力不够大, 因此最大值在限制中心2.25°左右波动. 然而, 我们似乎有很好的采样, 图告诉我们3°是窗口之间很好的分离间距. 因为直方图最大宽度的一半大约为6°. 我们可能会得到稍微宽一点的间距, 但保守点好. 我们也不需要过度担心最大的偏移量, 因为相邻的直方图足够重叠.

我们现在继续手动运行60°模拟, 因此我们需要为其他的模拟准备三个初始结构.

mdin_min.60 mdin_equi.60 mdin_prod.60 disang.60

mdin_min.60
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
2000 step minimization for 60 deg
 &cntrl
  imin = 1,
  maxcyc=2000, ncyc = 500,
  ntpr = 100, ntwr = 1000,
  ntf = 1, ntc = 1, cut = 8.0,
  ntb = 1, ntp = 0,
  nmropt = 1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.60
mdin_equi.60
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
50 ps NPT equilibration for 60 deg
 &cntrl
  imin = 0, ntx = 1, irest = 0,
  ntpr = 5000, ntwr = 50000, ntwx = 0,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 50000, dt = 0.001,
  tempi=0.0, temp0 = 300, ntt = 3,
  gamma_ln = 1.0,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.60
mdin_prod.60
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
100 ps NPT production for 60 deg
 &cntrl
  imin = 0, ntx = 5, irest = 1,
  ntpr = 10000, ntwr = 0, ntwx = 10000,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 100000, dt = 0.001,
  temp0 = 300.0, ntt = 3,
  gamma_ln = 1,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1, ioutfm = 1,
 &end
 &wt
  type='DUMPFREQ', istep1=50,
 &end
 &wt
  type='END',
 &end
DISANG=disang.60
DUMPAVE=dihedral_60.dat
disang.60
1
2
3
4
5
6
Harmonic restraints for 60 deg
 &rst
  iat=9,15,17,19,
  r1=-120.0, r2=60.0, r3=60.0, r4=240.0,
  rk2=200.0, rk3=200.0,
 /

需要注意的是, 这次使用的输入结构是ala_tri_prod_120.rst file, 为运行120°模拟后产生的文件.

mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_min.60 -o ala_tri_min_60.out -p ala_tri.prmtop -c ala_tri_prod_120.rst -r ala_tri_min_60.rst
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_equi.60 -o ala_tri_equil_60.out -p ala_tri.prmtop -c ala_tri_min_60.rst -r ala_tri_equil_60.rst
mpirun -np 2 $AMBERHOME/bin/pmemd.MPI -O -i mdin_prod.60 -o ala_tri_prod_60.out -p ala_tri.prmtop -c ala_tri_equil_60.rst -r ala_tri_prod_60.rst -x ala_tri_prod_60.nc

产生文件: ala_tri_min_60.out, ala_tri_min_60.rst, ala_tri_equil_60.out, ala_tri_equil_60.rst, ala_tri_prod_60.out, ala_tri_prod_60.rst, ala_tri_prod_60.nc, dihedral_60.dat

你应该再次检查采样是否良好, 检查直方图等等:

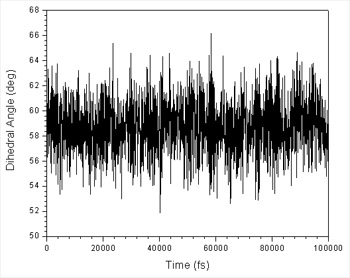
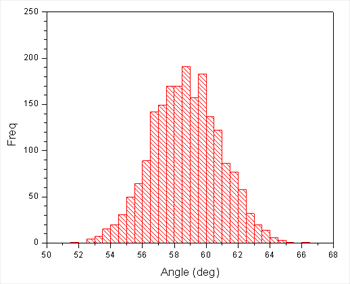
图10

脚本运行

既然已经有了做所有计算的起始结构, 我们可以写个脚本去产生所有输入文件, 除了120°和60°, 因为我们已经算过了. 我写的下面这个perl脚本既能产生输入文件, 也可以提交计算任务到San Diego超算中心(SDSC)的Teragrid IA64集群上. 你可能需要根据你自己的系统去修改它. 因为SDSC的每一个节点有两个处理器, 我将使用pmemd.MPI程序和2个处理器去运行每一个任务.

这些脚本基本相似, 不同的只有计算的角度范围. prepare_runs_0-90.perl脚本使用ala_tri_prod_60.rst文件作为起始结构运行0°到90°时所有计算. prepare_runs_93-147.perl脚本使用ala_tri_prod_120.rst作为起始结构运行93°到147°时所有计算. prepare_runs_150-180.perl使用03_equil.rst(180°)作为起始结构运行150°到180°时所有计算. 0到90°的例子如下:

perl
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#!/usr/bin/perl -w
use Cwd;
$wd=cwd;

print "Preparing input files\n";

$name="ala_tri";
$incr=3;
$force=200.0;

&prepare_input();

exit(0);

sub prepare_input() {

	$dihed=0;
	while ($dihed <= 90) {
	  if ($dihed != 60) {
	#skip 60 degrees since we already ran it
	print "Processing dihedral: $dihed\n";
	&write_mdin0();
	&write_mdin1();
	&write_mdin2();
	&write_disang();
	&write_batchfile();
	system("qsub run.pbs.$dihed");
	  }
	  $dihed += $incr;
	}
}

sub write_mdin0 {
	open MDINFILE,'>', "mdin_min.$dihed";
	print MDINFILE <<EOF;
2000 step minimization for $dihed deg
 &cntrl
  imin = 1,
  maxcyc=2000, ncyc = 500,
  ntpr = 100, ntwr = 1000,
  ntf = 1, ntc = 1, cut = 8.0,
  ntb = 1, ntp = 0,
  nmropt = 1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.$dihed
EOF
	close MDINFILE;
}
sub write_mdin1 {
	open MDINFILE,'>', "mdin_equi.$dihed";
	print MDINFILE <<EOF;
50 ps NPT equilibration for $dihed deg
 &cntrl
  imin = 0, ntx = 1, irest = 0,
  ntpr = 5000, ntwr = 50000, ntwx = 0,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 50000, dt = 0.001,
  tempi=0.0, temp0 = 300, ntt = 3,
  gamma_ln = 1.0,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1, ioutfm=1,
 &end
 &wt
  type='END',
 &end
DISANG=disang.$dihed
EOF
	close MDINFILE;
}
sub write_mdin2 {
	open MDINFILE,'>', "mdin_prod.$dihed";
	print MDINFILE <<EOF;
100 ps NPT production for $dihed deg
 &cntrl
  imin = 0, ntx = 5, irest = 1,
  ntpr = 10000, ntwr = 0, ntwx = 10000,
  ntf = 2, ntc = 2, cut = 8.0,
  ntb = 2, nstlim = 100000, dt = 0.001,
  temp0 = 300, ntt = 3,
  gamma_ln = 1.0,
  ntp = 1, pres0 = 1.0, taup = 5.0,
  nmropt = 1, ioutfm=1,
 &end
 &wt
  type='DUMPFREQ', istep1=50,
 &end
 &wt
  type='END',
 &end
DISANG=disang.$dihed
DUMPAVE=dihedral_${dihed}.dat
EOF
	close MDINFILE;
}
sub write_disang {
	$left  = sprintf "%4.1f", $dihed - 180;
	$min   = sprintf "%4.1f", $dihed;
	$right = sprintf "%4.1f", $dihed + 180;
	open DISANG,'>', "disang.$dihed";
	print DISANG <<;
Harmonic restraints for $dihed deg
 &rst
  iat=9,15,17,19,
  r1=$left, r2=$min, r3=$min, r4=$right,
  rk2=${force}, rk3=${force},
 &end
EOF
	close DISANG;
}

sub write_batchfile {
	open BATCHFILE, '>', "run.pbs.$dihed";
	print BATCHFILE <<EOF;
#PBS -l nodes=1:ppn=2
#PBS -l walltime=1:00:00
#PBS -N run_$dihed

cd $wd

mpirun -np 2 -machinefile \$PBS_NODEFILE pmemd.MPI -O \\
-i mdin_min.$dihed -p ${name}.prmtop -c ala_tri_prod_60.rst -r ${name}_min_${dihed}.rst  -o ${name}_min_${dihed}.out
mpirun -np 2 -machinefile \$PBS_NODEFILE pmemd.MPI -O \\
-i mdin_equi.$dihed -p ${name}.prmtop -c ${name}_min_${dihed}.rst  -r ${name}_equil_${dihed}.rst -o ${name}_equil_${dihed}.out
mpirun -np 2 -machinefile \$PBS_NODEFILE pmemd.MPI -O \\
-i mdin_prod.$dihed -p ${name}.prmtop -c ${name}_equil_${dihed}.rst -r ${name}_prod_${dihed}.rst -o ${name}_prod_${dihed}.out -x ${name}_prod_${dihed}.mdcrd
EOF

	print BATCHFILE "\necho \"Execution finished\"\n";
	close BATCHFILE;
}

我在SDSC Teragrid集群上运行所有计算. 整个耗时30分钟. 欢迎您尝试在自己的集群上运行这些程序, 或者您可以下载完整的输出文件(包括60到120°的): ala_tri_umbrella_run.tar.gz

在我们运行WHAM生成PMF这一最后阶段之前, 应该快速检查所有的窗口是否正确地重叠. 最简单的方法是在一个图上绘制所有的dihedral_xxx.dat数据点, 查看之间的空隙:

合并数据脚本:

#!/bin/csh
foreach i ( *.dat )
  echo $i
  cat $i >> all_dihedrals.dat
end

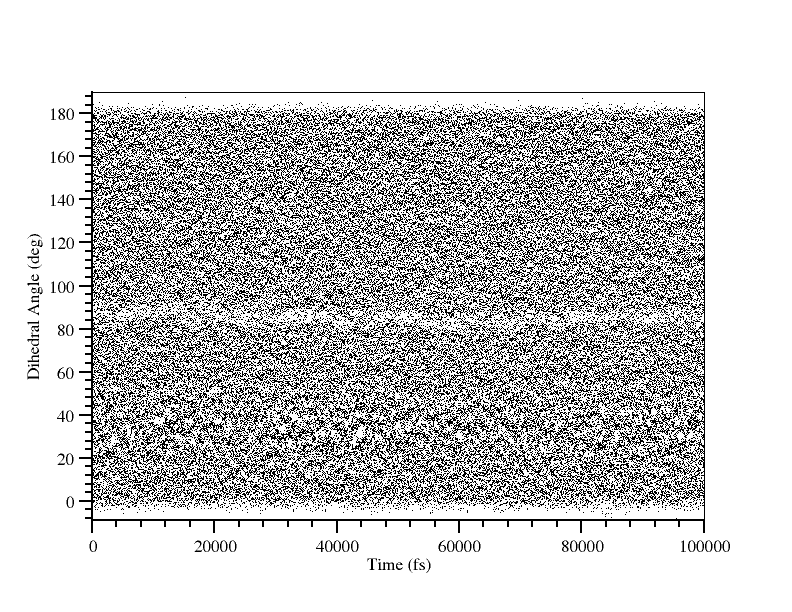
图11

图中并没有明显的间隙, 虽然在81°到87°附近的数据看上去有点粗略. 很可能这个区域处于过渡态附近. 我们手动画出78, 81, 84和90°时的直方图并检查他们的重叠:

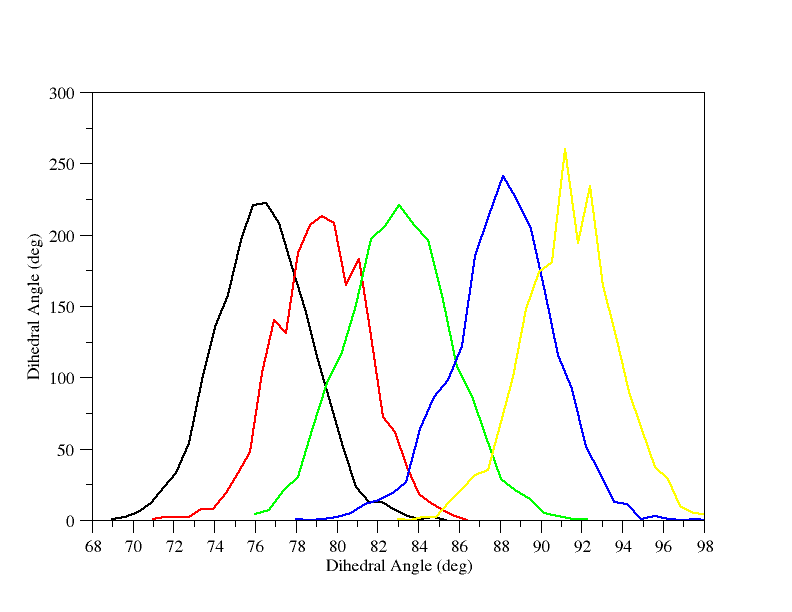
图12

这表明85°附近采样减少, 但我们任然有极好的重叠, 没什么问题

我们现在进入第三节, 将使用WHAM去产生PMF.

第三节: 产生PMF

伞形采样的最后阶段是使用Alan Grossfield的WHAM代码, 从我们采集到的二面角数据中产生PMF. WHAM确切的工作原理超出了本教程的范围, 教程的主要目的是展示怎样在AMBER中做伞形采样, 而不是提供一个关于伞形采样背后的理论知识. 为此, 你应该参考一些关于分子动力学和统计力学的最新课本.

WHAM代码由Alan Grossfield的网站提供, 可以下载它. (这儿也有来自网站的副本可以下载: wham-dist.tgz)

对于本教程, 假设你已经下载好了WHAM代码并且编译了它, 将编译好的放在了/uer/local/bin下. 添加它到你的路径下意味着你应该能通过输入wham去调用它. 从这点可以推断它正常工作了.

现在我们需要制作wham meta文件. 它本质上是个输入文件, 告诉了每个二面角文件的文件名, 简谐势的最小值和力常数是多少, 格式如下:

<filename> <harmonic potential minimum in deg> <force constant in the correct units>

单位的注意: Amber使用k(x-x0)2, 这里k的单位是kcal/mol/rad2, 而WHAM程序使用0.5k(x-x0)2, k的单位kcal/mol/deg2. 因此我们必须加上原始的力常数(在这里是200.0), 通过2(pi/180)2 = 0.0006092换算. 因此力常数用WHAM中的单位表示为: 0.12184 kcal/mol/deg2.

下面的脚本将为我们创建meta.dat文件:

create_meta.perl
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#!/usr/bin/perl -w
use Cwd;
$wd=cwd;

print "Preparing meta file\n";

$name="meta.dat";
$incr=3;
$force=0.12184;

&prepare_input();

exit(0);

sub prepare_input() {

	$dihed=0;
	while ($dihed <= 180) {
	  print "Processing dihedral: $dihed\n";
	  &write_meta();
	  $dihed += $incr;
	}
}

sub write_meta {
	open METAFILE,'>>', "$name";
	print METAFILE <<EOF;
dihedral_$dihed.dat $dihed.0 $force
EOF
	close MDINFILE;
}

图13

生成文件: meta.dat

接下来我们运行wham:

wham P -1 181 61 0.01 300 0 meta.dat result.dat

在这里:

WHAM按照以下步骤运行:

  1. 制作直方图
  2. 依据所使用的势调整直方图
  3. 转换每一个直方图为自由能曲线段
  4. 使用最小二乘法拟合迭代式的排列所有曲线段
  5. 写入完整的PMF曲线到输入文件中

这将产生result.dat文件.

我们提取输出文件的前两列, 然后绘制它:

cat result.dat | awk '{print$1,$2}' > pmf.dat

产生文件: pmf.dat

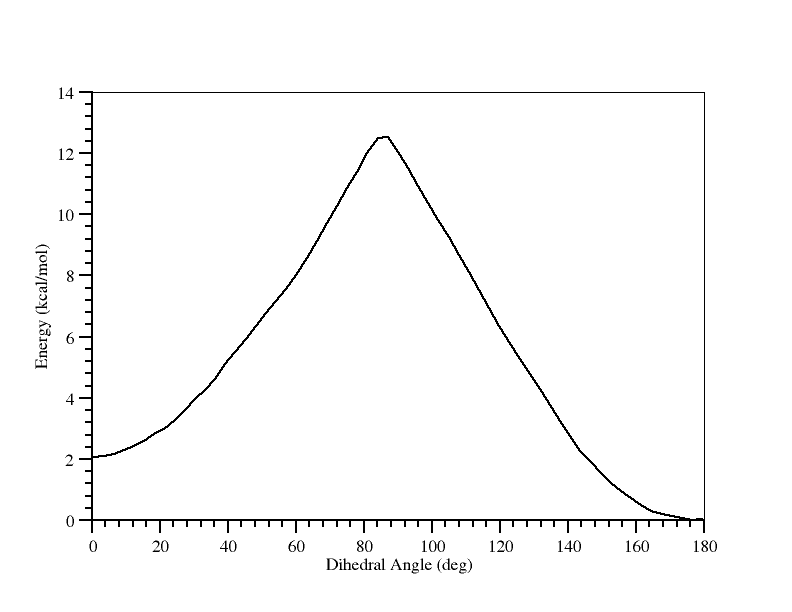
你已经绘制了它. 这告诉了我们反式比顺式结构更为稳定, 约1.8 kcal/mol, 从反式到顺式的转换需要的能垒大约为12.1 kcal/mol.

如果你够大胆, 你现在可以尝试用QM/MM去重复, 或者甚至使用QM/MM做简单的反应.

◆本文地址: , 转载请注明◆
◆评论问题: https://jerkwin.herokuapp.com/category/3/博客, 欢迎留言◆
前一篇:　GROMACS自由能计算中软核势的使用
后一篇:　xpm文件处理脚本
访问人次(2015年7月 9日起): | 最后更新: 2024-11-01 02:53:58 UTC | 版权所有 © 2008 - 2024 Jerkwin 个