- 2018-08-29 21:51:38
Pi-Pi堆积的概念和意义
略
Pi-Pi堆积的表征量
表征Pi-Pi堆积的物理量一般使用两个, 距离和角度. 距离为某一组原子质心或中心到另一组原子所在平面的距离, 角度为两组原子所在平面之间的夹角. 计算这两个量就需要知道如何计算一组原子所在平面的方程. 对于完全刚性的平面组原子, 三个非共线原子就可以确定其所在的平面方程(平面的三点式方程). 对于近似刚性的原子组, 则需要通过多元线性拟合来确定平面方程.
有了平面方程 $ax+by+cz+d=0, \vec n=(a,b,c)$, 可计算空间一点 $\vec r(x,y,z)$ 到平面的距离
\[d={\vec r \cdot \vec n +d\over \abs {\vec n} }\]也可计算此点到平面的垂足
\[\vec v=\vec r - {\vec n \cdot \vec r+d \over \abs{\vec n}^2} \vec n\]Pi-Pi堆积量的计算
gmx analyze可以进行多元线性拟合得到平面方程. 通过脚本调用即可, 虽然麻烦但不困难, 就不再示例了.
这里我们用vmd加上tcl数学库来进行计算. vmd并没有自带这个库, 须自行安装. 我们只需要其中的线性代数库linalg.tcl, 其中包含了多元线性拟合的奇异值分解算法leastSquaresSVD, 使用倒也方便. 这里多说一句, vmd加上tcl的数学库后基本可以进行各式分析了, 虽然速度未必佳.
既然是决定用vmd进行分析了, 那顺便也学习一下vmd的绘图方法吧. 将计算结果实时显示出来, 也更容易确定计算结果是否正确.
代码
见 gmxtool
使用方法
得到了轨迹以后, 先对轨迹进行处理: 分子完整化, , 然后就可以计算Pi-Pi堆积量了.
- 运行MD模拟, 获得轨迹
- 对轨迹进行处理: 先
gmx trjconv -pbc whole完整化分子, 再gmx trjconv -center -fit rot+trans对分子进行居中叠合 - vmd载入轨迹:
vmd conf.gro traj.xtc - 修改
pistack.tcl中的两个原子组 - vmd命令窗口执行
source pistack.tcl - 分析得到的输出文件
pistack.xvg, 也可以播放轨迹, 查看每一帧计算结果
示例
两个苯分子的模拟
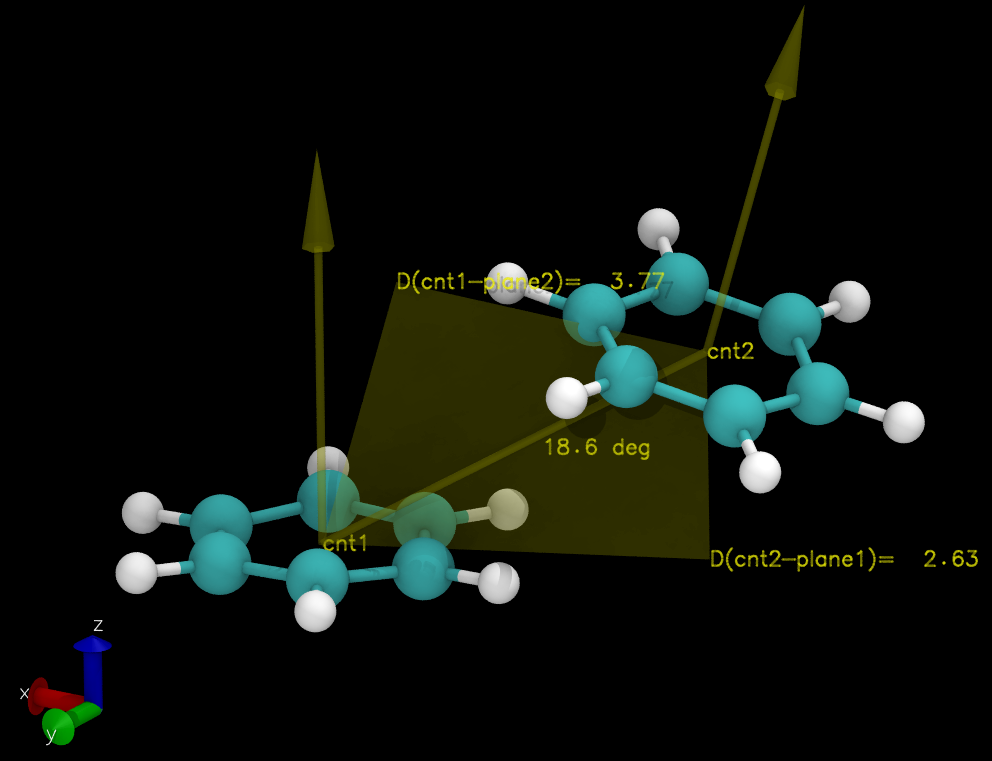
输出文件pistack.xvg中每行数据会依次列出
- 轨迹帧的编号
- 每帧中每组原子的中心:
Xcnt(1) Ycnt(1) Zcnt(1),Xcnt(2) Ycnt(2) Zcnt(2) - 每组原子所在平面方程的系数:
a(1) b(1) c(1),a(2) b(2) c(2) - 两平面的夹角:
A(n1,n2) - 第一组原子中心到第二组原子所在平面的距离:
D(c1,p2) - 第二组原子中心到第一组原子所在平面的距离:
D(c2,p1).
存在问题
- 轨迹过大时速度不佳
- 考虑到周期性边界条件, 所得距离和角度可能存在不连续性
- vmd每帧绘制时
draw material Transparent似乎不起作用? 必须存在错误语句才可以? - tcl是totally command language, 也是toy command language, 太(Tai)差(Cha)了(Le)
