- 2019-04-21 06:37:43 整理: 李赟, 刘庭崧; 统稿/代码: 李继存
水分子的序参数有很多种, 不同序参数的计算方法也不尽相同. GROMACS自带的分析程序gmx h2order可以计算其中的两种序参数, 对于这种可以直接使用已有命令进行计算的序参数, 就无需赘言了.
有些序参数的计算比较复杂, 没有直接可以使用的命令, 这时就需要我们自己进行计算. 如果你会写代码计算就容易些, 否则的话, 或者到网上寻找已有的代码/脚本, 或者咨询/求助下有经验的人.
如果你确定要自己写代码进行计算, 那我的建议还是和以前一样: 充分利用GROMACS已有的功能和自带的工具, 使用简单的脚本组合其输入输出, 整理所得的数据, 获得自己需要的结果. 这种做法比你从头写一个分析程序简单不少, 因为你不需要自己读取轨迹, 处理PBC, 查找原子, 也不需要计算距离, 角度等, 只需要想清楚计算流程, 将需要执行的步骤写在脚本中就可以了. 当然, 有时还是需要进行一些简单的中间处理, 但大多是准备脚本所需要的输入和输出.
本教程就以一个比较复杂的序参数来示例下具体的操作过程, 做法与以前氢键数目的计算类似, 只不过稍微复杂一些.
背景及定义
在水合物的模拟中, 常会使用角度序参数AOP(angular order parameter), 三体序参数F3(也称四面体序参数, tetrahedral order parameter)和四体序参数 F4(four-body order parameter)来表征水分子所处的状态. 其中AOP和F3是相同的序参数, 只是叫法不同而已, 所以不需要进行区分. 一般来说, 在文章中如果只讨论F3, 那大多会称其为AOP或F, 如果同时还讨论F4, 那多半会称其为F3, 而不称AOP或F.
F3序参数
AOP/F3是一个由三体(三个水分子)构型组成的参数, 表征了中心氧原子与周围3.5Å范围内的其他氧原子形成的四面体与正四面体的偏离程度. 其计算公式如下:
\[\alg \text{AOP}/F_3 &= {1\over n_i(n_i-1)/2}\sum_{j=1}^{n_i-1} \sum_{k=j+1}^{n_i} \left( \left| \cos\theta_{jik} \right|\cos\theta_{jik} + \cos^2(109.47^\circ) \right)^2 \\ &= {1\over n_i(n_i-1)/2}\sum_{j=1}^{n_i-1} \sum_{k=j+1}^{n_i} \left( \left| \cos\theta_{jik} \right|\cos\theta_{jik} + {1\over9} \right)^2 \ealg\]所涉及的角度为中心水分子的氧原子i与其周围3.5Å范围内任意两个其他水分子的氧原子j和k之间的夹角, 其中109.47度为正四面体中心-顶点连线之间夹角, 也是3维空间中4个向量间最小夹角的最大值 \(\arccos \left({-1 \over 3}\right)=2\arctan(\sqrt 2)≈109.4712°\)
有文献中认为109.47°是水分子的键角, 也有文献中对此角度使用水分子的键角, 这些都是不正确的.
本质上说, AOP/F3就是判断中心氧原子周围的氧原子是否处于四面体的角度位置. 但涉及具体的公式, 在文献上有几种不同的版本. 主要区别在于:
- 是否平方
- 是否对角度数目进行平均
- 是否要乘以10, 以方便与F4对比显示
- 使用哪个角度
不同版本所得的AOP/F3对一些特殊体系的值是不同的. 比如, 文献上水合物AOP/F3常见的值就有两个, 0.1, 或0.01. 对本文最后所给的几篇参考文献进行统计, 所得结果如下
| 方法 | 冰 | 固态水 | 水合物 | 液态水 |
|---|---|---|---|---|
| 平方/平均/键角 | 0 | 0.1 | ||
| 平方/平均/键角 | 0 | 0.1 | ||
| 平方/平均 | ||||
| 平方/平均 | 0.01 | 0.1 | ||
| 平方/平均 | 0 | 0.1 | 0.8 | |
| 平方/未平均 | 0 | 0.1 | 0.8, 界面 0.4 | |
| 平方/未平均 | 0 | 0.02 | ||
| 平方/未知 | 0.01 | 0.1 | ||
| 未平方/平均/10倍 | 0.1 | 0.9 | ||
| 未知 | 0.01 | 0.1 |
可见, 大多数关于水合物模拟的文献采用的计算公式都与上文的定义相同. 在这种定义下, 固态水和水合物的AOP/F3为0.01, 而液态水的AOP/F3为0.1. 液态水AOP/F3为0.8的两篇文献来自同一个研究组, 但给出的公式却不一致, 可以推测他们没有注意到这个问题.
我们来比较下平方和未平方版本公式对角度的依赖性.
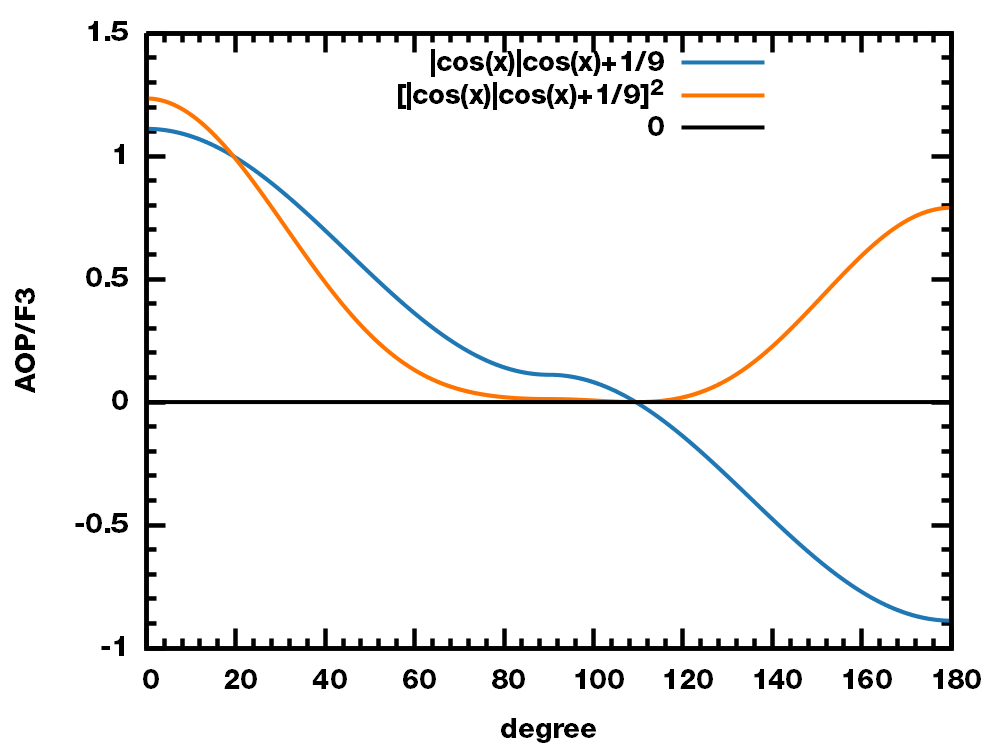
平方版本所得的AOP/F3在100度附近AOP/F3对角度变化不敏感, 这样力场, 温度等对其影响较小.
如果我们假定每个角度都是独立的, 那么根据空间中两随机向量间夹角的概率密度分布为 $p(\q)={1 \over 2}\sin\q$, 由此可以得到F3的平均值为
\[\alg \left< F_3 \right> &=\int_0^\p F_3(\q) p(\q) d\q=\int_0^\p {1\over 2} \left( |\cos\q| \cos\q+{1\over9} \right)^n \sin\q d\q \\ &= \begin{cases} {1 \over 9} \approx 0.11111 & n=1 \\ {86 \over 405} \approx 0.21235 & n=2 \end{cases} \ealg\]由于所得结果与液态水的AOP/F3值存在很大差距, 我们可以认为在液态水中, 对应的夹角并不是随机分布的.
F4序参数
F4统计的是水体系中两个相邻水分子最外侧氢原子以及水分子中氧原子组成二面角:
\[F_4 = {1\over n}\Sum_{i=1}^n \cos 3\phi_i\]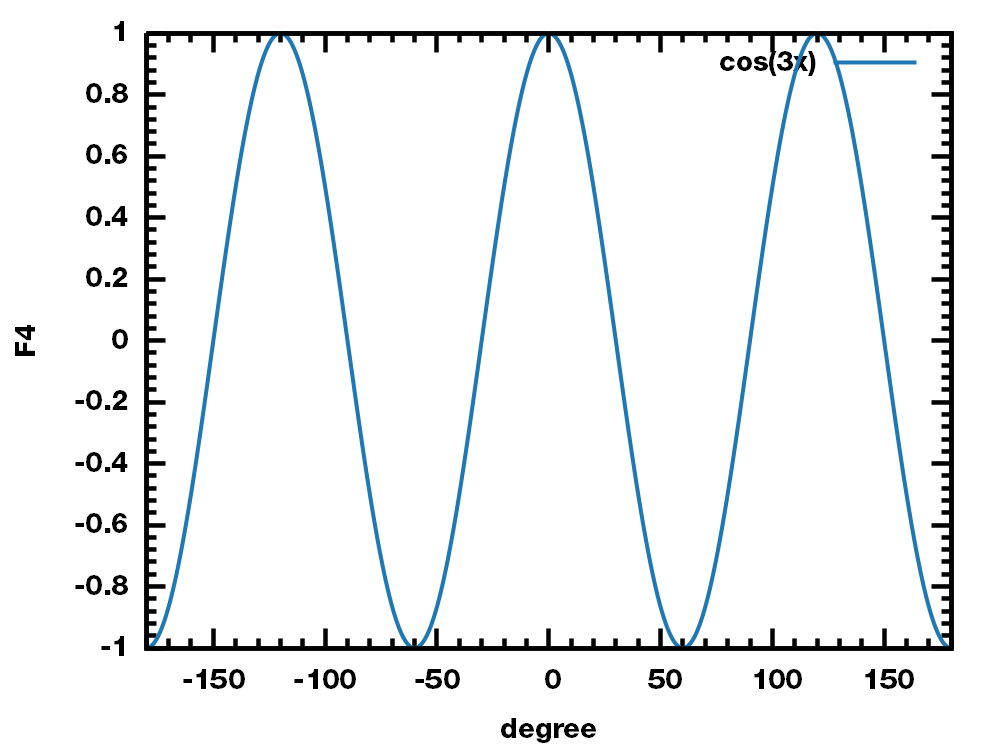
一些体系的F4值: 冰 -0.4(Ice-Ih -0.5; Ice-II -0.3; Ice-IV -0.4); 液态水 -0.04; 水合物 0.7(sI型 0.89; sII型 0.96).
对正四面体的冰, 其F4精确值为
\[\alg 4F_4 &= \cos(3\times 120°) +\cos(3\times 180°) \\ &+\cos(3\times -60°)+\cos(3\times 60°)=-2 \ealg\]当然, 实际的冰有多种结构, 所以其F4值并不精确地等于-0.5. 这就是为什么文献上经常会使用-0.4的原因.
AOP/F3, F4的值对于固态水(水合物与冰)和液态水有较大差别, 都可用于判定某区域内水分子的相态情况. 但相对而言, F4的表征能力更好一些, 因为AOP/F3不包括氢原子的信息, 不容易区分各种固态结构的水. 因此很多文章直接使用F4, 而没有给出AOP/F3.
计算流程
AOP/F3的计算
理解了定义, 那我们来看一下, 如何计算AOP/F3
最简单最直接, 也是最容易想到的方法就是, 对每一帧轨迹中每个需要考虑的水分子, 查找距离其氧原子3.5 Å之内的其他氧原子, 对于找到的这些氧原子, 计算其中任意两个与中心氧原子所成角度, 然后根据定义计算相应的AOP/F3值.
具体来说, 如果中心氧原子的编号为 $I_0$, 距离其3.5Å之内的其他氧原子的编号为 $I_1$, $I_2$, $I_3$, $I_4$, …, $I_n$, 那么可能的角度总数为C(n,2)=n(n-1)/2, 这些角度的编号三联对为 $I_1 I_0 I_2$, $I_1 I_0 I_3$, $I_1 I_0 I_4$, …, $I_1 I_0 I_n$, $I_2 I_0 I_3$, $I_2 I_0 I_4$, …, $I_2 I_0 I_n$, …, $I_{n-1} I_0 I_n$.
所以, 我们需要做的工作包括下面几点
- 对于指定的中心氧原子 $I_0$, 查找距其3.5 Å之内的其他氧原子的编号$I_1$, $I_2$, …, $I_n$.
gmx select可以做到 - 根据 $I_0$, $I_1$, $I_2$, …, $I_n$, 生成角度编号三联对$I_1 I_0 I_2$, $I_1 I_0 I_3$, …, $I_{n-1} I_0 I_n$. 自己写代码
- 根据角度编号三联对, 计算角度值.
gmx gangle可以做到 - 根据角度值, 计算AOP/F3. 自己写代码
所以, 任务分解后, GROMACS自带的工具可以帮我们完成计算最复杂的部分, 我们要做的只是简单的处理输入输出.
假定我们的要计算的中心氧原子编号为$cntAtom, gro结构文件名称为$conf, 水中氧原子的名称为OW,
对于任务1, 我们需要的执行的命令如下
gmx select -f $conf.gro -on $conf.ndx -s -quiet << EOS
r = distance from atomnr $cntAtom
atomname OW and 0. < r and r <.35
EOS执行成功后, 得到的氧原子编号在输出的$conf.ndx中.
对于任务2, 我们需要读取$conf.ndx中的原子编号, 然后生成角度三联对. 这不是困难的任务, 只要一个双重循环就好了, 可以使用你熟悉的任何语言来实现. 我们将角度编号三联对放到另一个索引文件$pid.ndx中.
对于任务3, 指定前面得到的索引文件中的角度三联对, 直接调用命令即可
gmx gangle -f $conf.gro -n $pid.ndx -group1 0 -s -oall -quiet这样在默认的输出文件angles.xvg中就得到了所有的角度值.
对于任务4, 我们需要自己处理下得到的角度. 就简单的方法就是将这个文件的内容追加到一个另外的数据文件中, 然后用自己熟悉的工具来计算AOP/F3. 当然, 也可以一步到位, 直接将AOP/F3输出到数据文件中.
F4的计算
F4的计算也是类似, 但可能更麻烦. 因为在定义中角度 $\f$ 对应距离最远的两个氢原子, 这意味着我们不仅要知道需要的氧原子, 还要确定出对应的4个氢原子对中哪一对的距离最远, 从而计算相应的二面角. 所以我们需要增加一步计算并比较距离的任务, 从而才能得到所需要的二面角编号四联对. 距离的计算最好还是借助gmx distance, 避免自己写代码.
具体来说, 主要包括以下几点
第一步: 输出与中心氧原子, 选中氧原子对应的氢原子的距离编号对.
第二步: 根据上一步得到的氢原子编号对, 通过命令计算出4对氢原子的距离.
gmx distance -f $conf.gro -n $pid.ndx -select 0 -s -oall -quiet第三步: 根据距离的最大值确定要计算的二面角, 并输出要计算二面角的编号四联对.
第四步: 直接调用命令计算二面角.
gmx gangle -f $conf.gro -n $pid.ndx -g1 dihedral -group1 0 -s -oall -quiet最后, 用自己熟悉的工具处理下得到的二面角, 将F4输出到数据文件中.
完成脚本
我们已经知道如何处理一帧构型, 那就将其变为一个脚本AOP.bsh, 其命令行参数只有一个, 那就是每帧的编号, 这样就可以借助gmx trjconv -exec功能处理所有的轨迹帧了.
总结一下流程就是:
- 完成一个脚本可以处理单帧构型. 你可以借助GROMACS的工具, 也可以使用自己的方法来处理.
- 使用
gmx trjconv -exec执行此脚本, 处理所有的帧. 当然, 你也可以先输出所有的帧, 然后脚本处理, 虽然麻烦一些.
示例脚本
| AOP.bsh | |
|---|---|
1 | (略) |
使用的时候只需要修改中心氧原子的编号cntAtom即可. 具体来说
for cntAtom in {第一个氧原子编号..最后一个氧原子编号..3}`其中的3表示使用的水模型为三位点水模型, 如SPC, SPC/E, TIP3P等. 如果你使用四位点水模型, 如TIP4P, 应相应地改为4. 此外, 这种简单的循环方式只适用于连续的水分子, 且其中的原子排列顺序为OW HW1 HW2. 如果你的所有水分子在整个体系的编号系统中被其他分子分成了好几个部分, 那你或者不使用这中简单的循环方式, 或者分别计算每部分水分子.
说明:
gmx gangle是支持选区, 但我们没法直接提供要计算的角度编号三联对, 因为gmx select动态选区语法不够强大. 如果gmx select能够支持组合所选原子的编号, 那计算F3需要的角度只要简单的使用gmx gangle就可以了.gmx gangle计算时对角度编号三联对的数目有限制, 具体多大没有仔细考察. 但如果使用的截断距离扩大10倍, 达到35Å, 那在8GB内存的Windows下是无法处理的.- 我们将所有的计算流程都写在一个脚本中: 自动生成处理每帧的的脚本, 自动调用
gmx trjconv. 实际上你也可以自己创建一个脚本, 自己执行.
脚本测试示例
示例1: IceIh_Hayward冰
IceIh_Hayward冰结构来自以前的博文常见冰的晶体结构及其cif文件. 下图为其晶体结构:
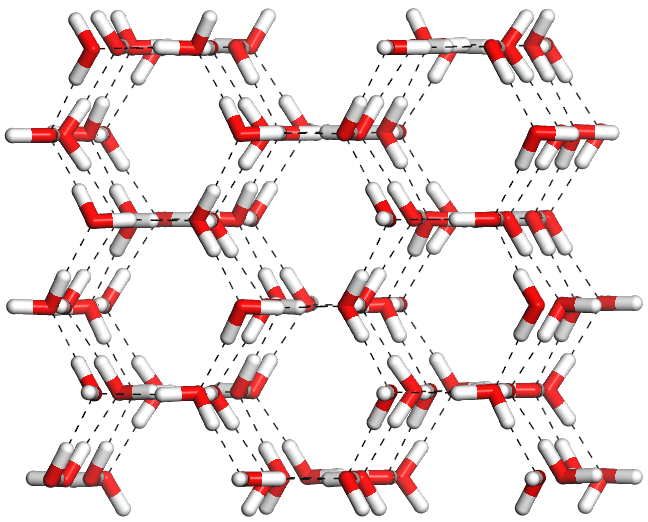
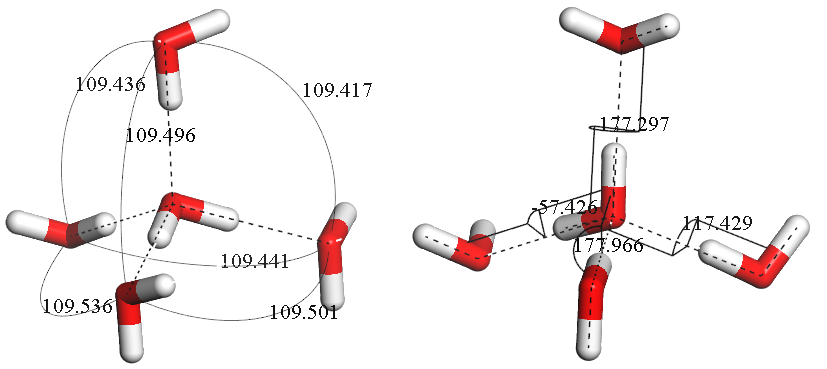
我们任意选取其中的两个中心氧原子进行计算, 例如: 10号氧原子(坐标3.38 2.60 5.06), 70号氧原子(坐标5.63 6.50 5.06). 使用Materials Studio(也可采用VMD, Chemcraft, GaussView等)软件测量周围原子与中心原子所成的角度和二面角.
- 10号氧原子:
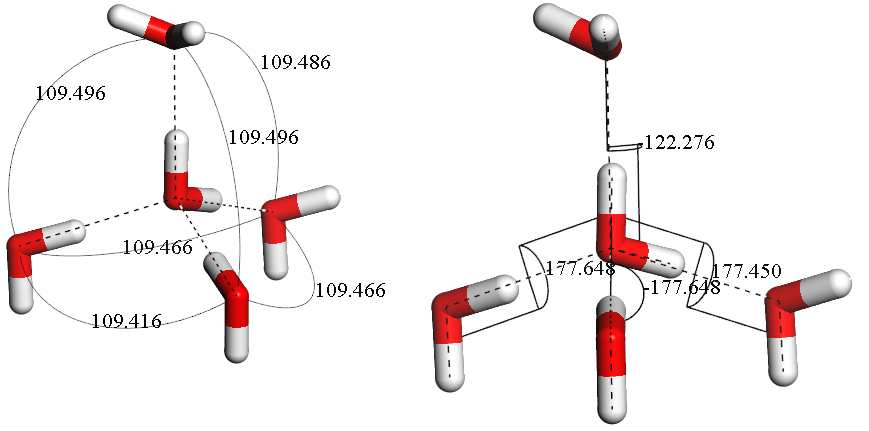
- 70号氧原子:
修改AOP.bsh脚本中的中心原子编号得到不同中心氧原子的计算结果, 将其与软件测量的结果进行对比:
| 氧原子 | 方法 | $\q_1$ | $\q_2$ | $\q_3$ | $\q_4$ | $\q_5$ | $\q_6$ | AOP/F3 |
|---|---|---|---|---|---|---|---|---|
| 10号 | 测量 | 109.496 | 109.486 | 109.496 | 109.466 | 109.416 | 109.466 | 0 |
| 脚本 | 109.496 | 109.486 | 109.496 | 109.466 | 109.416 | 109.466 | 0 | |
| 70号 | 测量 | 109.496 | 109.536 | 109.501 | 109.436 | 109.417 | 109.441 | 0 |
| 脚本 | 109.496 | 109.536 | 109.501 | 109.436 | 109.417 | 109.441 | 0 |
| 氧原子 | 方法 | $\f_1$ | $\f_2$ | $\f_3$ | $\f_4$ | F4 |
|---|---|---|---|---|---|---|
| 10号 | 测量 | -122.276 | 177.648 | 177.450 | -177.648 | -0.49575 |
| 脚本 | -119.820 | 180.000 | 180.000 | 180.000 | -0.500011 | |
| 70号 | 测量 | -57.426 | 117.429 | 177.297 | 177.966 | -0.49605 |
| 脚本 | -59.794 | 119.820 | -179.200 | 179.329 | -0.49962 |
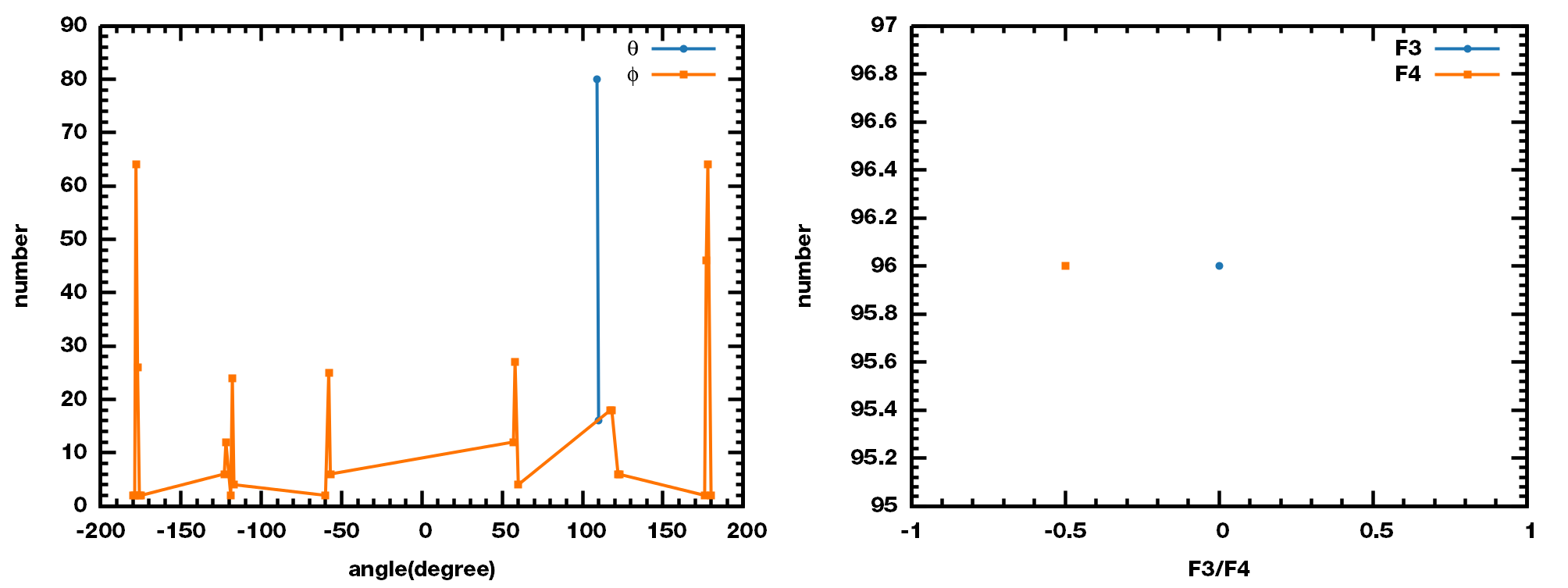
$\q$, $\f$, F3和F4的分布如下
示例2: I型甲烷水合物
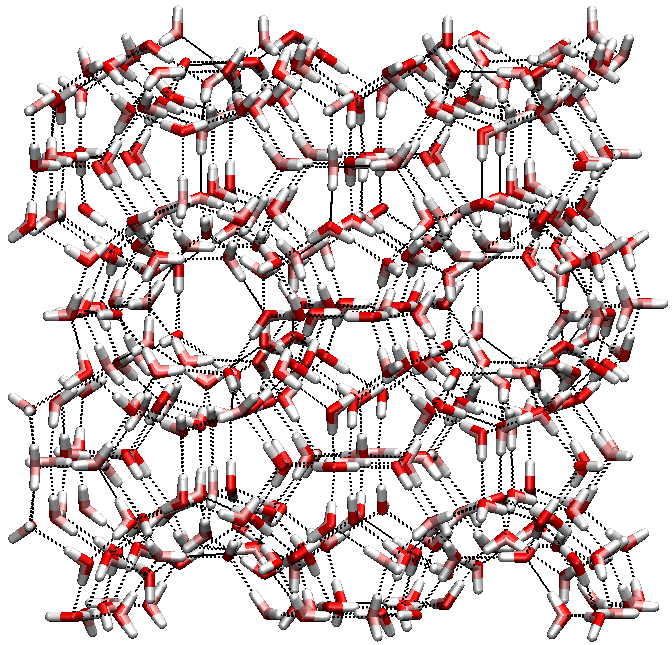
采用与示例1相同的方法和步骤, 我们计算了I型甲烷水合物结构中水分子的序参数. I型甲烷水合物中的水分子为四位点的TIP4P模型. 下图为I型甲烷水合物的晶体结构.
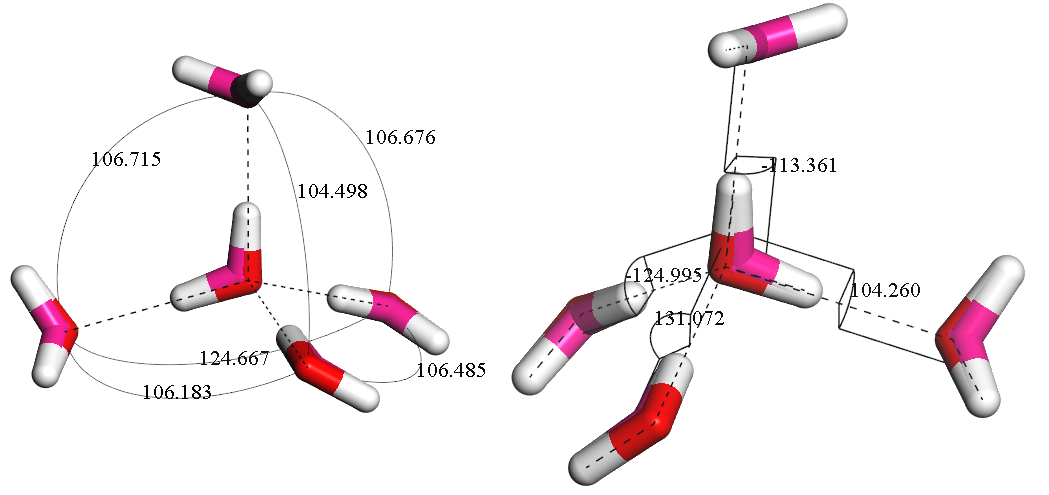
我们选取结构中的17号氧原子进行计算(坐标14.180 12.790 16.450). 使用Materials Studio软件测量得到周围原子与17号氧原子所成角度和二面角大小.
与示例1相同, 修改AOP.bsh脚本中的中心原子编号得到计算结果, 并将其与软件测量结果进行对比.
| 方法 | $\q_1$ | $\q_2$ | $\q_3$ | $\q_4$ | $\q_5$ | $\q_6$ | AOP/F3 |
|---|---|---|---|---|---|---|---|
| 测量 | 106.715 | 106.676 | 104.498 | 124.667 | 106.183 | 106.485 | 0.008527 |
| 脚本 | 106.715 | 106.676 | 104.498 | 124.667 | 106.183 | 106.485 | 0.008527 |
| 方法 | $\f_1$ | $\f_2$ | $\f_3$ | $\f_4$ | F4 |
|---|---|---|---|---|---|
| 测量 | 104.260 | -113.361 | -124.995 | 131.072 | 0.8555 |
| 脚本 | 104.260 | -112.915 | -124.995 | 131.413 | 0.850963 |
$\q$, $\f$, F3和F4的分布如下
说明
- 上述两个示例中脚本计算的二面角与软件测量结果存在微小差别. 这是因为GROMACS输出的
gro文件中坐标的精度有限, 对某些原子的坐标有时候会与原始文件中的存在差别. 如果gro文件中输出的坐标位数多一些就不会存在这些问题(新版本GROMACS不再支持变精度的gro文件). 因此, 我们在验证过程中可以使用gmx trjconv输出的构型文件来代替原始的构型文件. - 如果使用
AOP.bsh脚本计算整个模拟时间段内序参数的变化, 可能需要很长时间. 简单的解决方法是采用并行, 将轨迹复制多份, 每份只计算一段时间的序参数, 然后再合并结果. - 在计算AOP/F3时, 中心氧原子周围至少需要有2个其他氧原子. 如果只有一个其他氧原子, 会无法计算角度从而导致程序出错, 但是计算结果中不会包含出错的数据, 所得结果正常.
示例3: TIP3P水
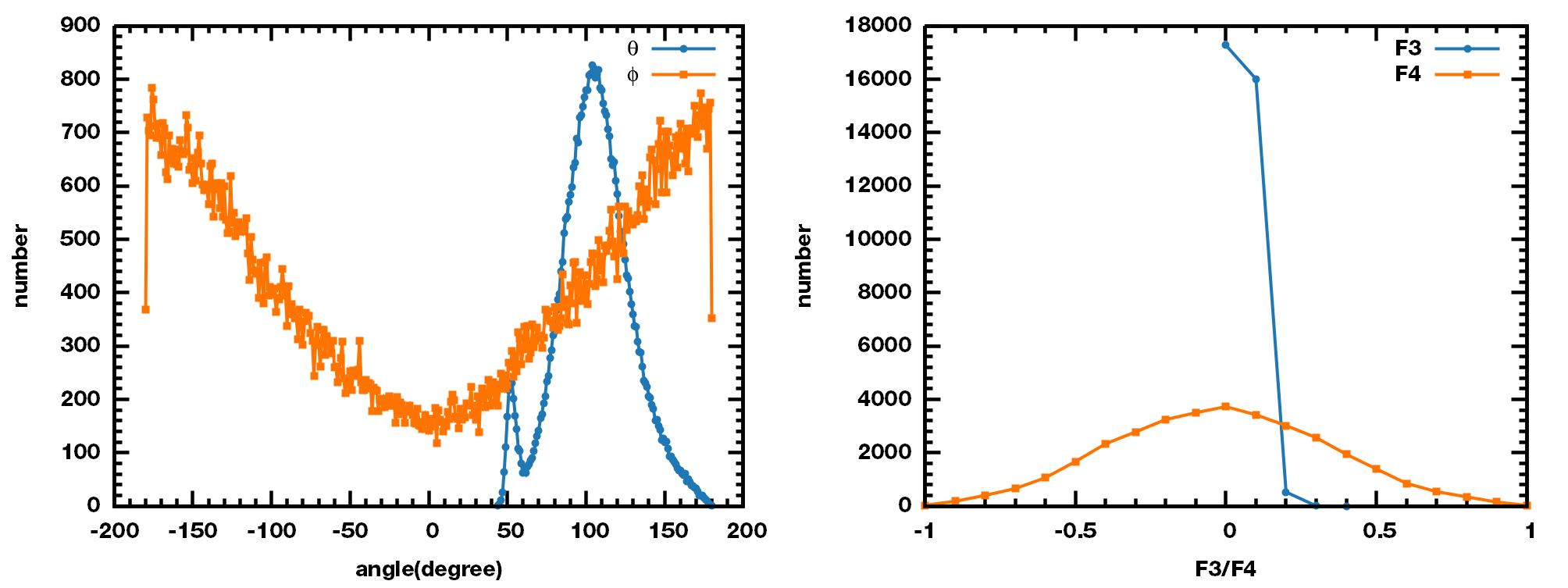
使用GROMACS自带的spc216.gro作为初始构型, 采用TIP3P水模型运行200 ps模拟.
计算得到水合物生成过程中F3/F4的变化如下图.
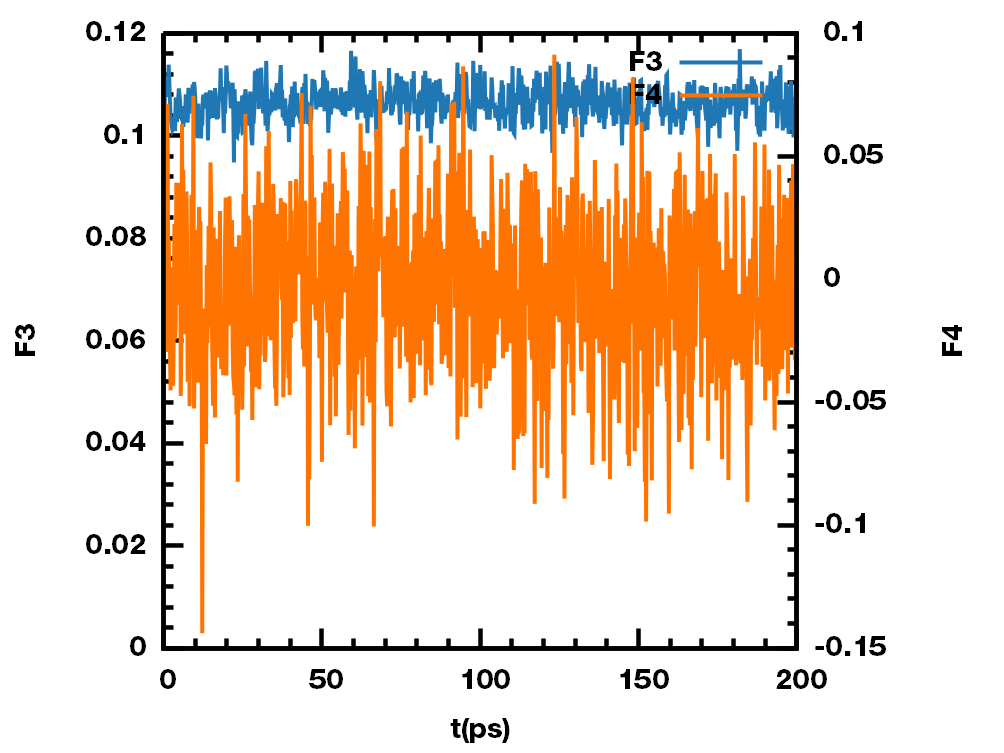
可见, 我们得到的F3在0.1附近, 这与前面所讲的一致.
$\q$, $\f$, F3和F4的分布如下
快一些
脚本写起来简单, 因此上面这种组合GROMACS工具的方法有其方便之处, 但如果要计算的数据太过复杂, 脚本处理起来就比较麻烦, 而且计算速度也很慢, 因此, 组合脚本的方法不适用于计算太复杂的数据, 处理长时间的轨迹. 对于我们的情况, F3使用脚本计算还算简单, 但F4使用脚本计算就已经很麻烦了. 是时候考虑下使用编译型语言来提高计算速度了.
简单的提速方法是不再调用GROMACS工具来计算角度, 距离等, 而是直接使用脚本所需要的数据. 但这种方法受限于脚本的运行速度, 效果可能仍然不够理想. 因此, 我们需要考虑使用编译型语言来处理. 推荐使用C/C++, 或Fortran.
因为我熟悉Fortran, 所以就使用Fortran编写了序参数的计算代码.
示例代码
| AOP.f90 | |
|---|---|
1 | (略) |
代码使用示例
先编译好AOP.f90代码, 并在gmx trjconv命令中进行调用
echo 0 | gmx trjconv -f traj_comp.xtc -s -n -o traj.gro -sep -exec 'AOP.exe traj.gro index.ndx OW OW 3.5 XYZ'注意, index.ndx中氧原子组的名称必须和程序参数指定的一致. AOP.exe此项默认氧原子的名称为OW.
此外, 你也可以先将要计算的水分子的坐标抽取出来, 保存为traj.gro, 然后直接运行程序. 但在这种情况下需要使用traj.gro重新创建index.ndx, 因为traj.gro中的氧原子编号可能会与原始轨迹中的不同.
示例4: 甲烷水合物
我们通过从甲烷水合物轨迹中选取的几帧构型来验证bash脚本和fortran代码计算结果的一致性. 结果如下图所示.
| 序参数 | 方法 | 0 ps | 5 ps | 10 ps | 15 ps | 20 ps | 25 ps | 30 ps |
|---|---|---|---|---|---|---|---|---|
| F3 | Bash | 0.0566 | 0.0565 | 0.0567 | 0.0570 | 0.0569 | 0.0578 | 0.0591 |
| Fortran | 0.0566 | 0.0565 | 0.0567 | 0.0570 | 0.0569 | 0.0578 | 0.0591 | |
| F4 | Bash | -0.0478 | -0.0283 | -0.0338 | -0.0265 | -0.0149 | -0.0281 | -0.0189 |
| Fortran | -0.0479 | -0.0283 | -0.0338 | -0.0264 | -0.0149 | -0.0281 | -0.0190 |
可见二者所得结果一致, 这说明代码中涉及PBC处理, 距离和角度计算的部分是正确的.
$\q$, $\f$, F3和F4的分布如下
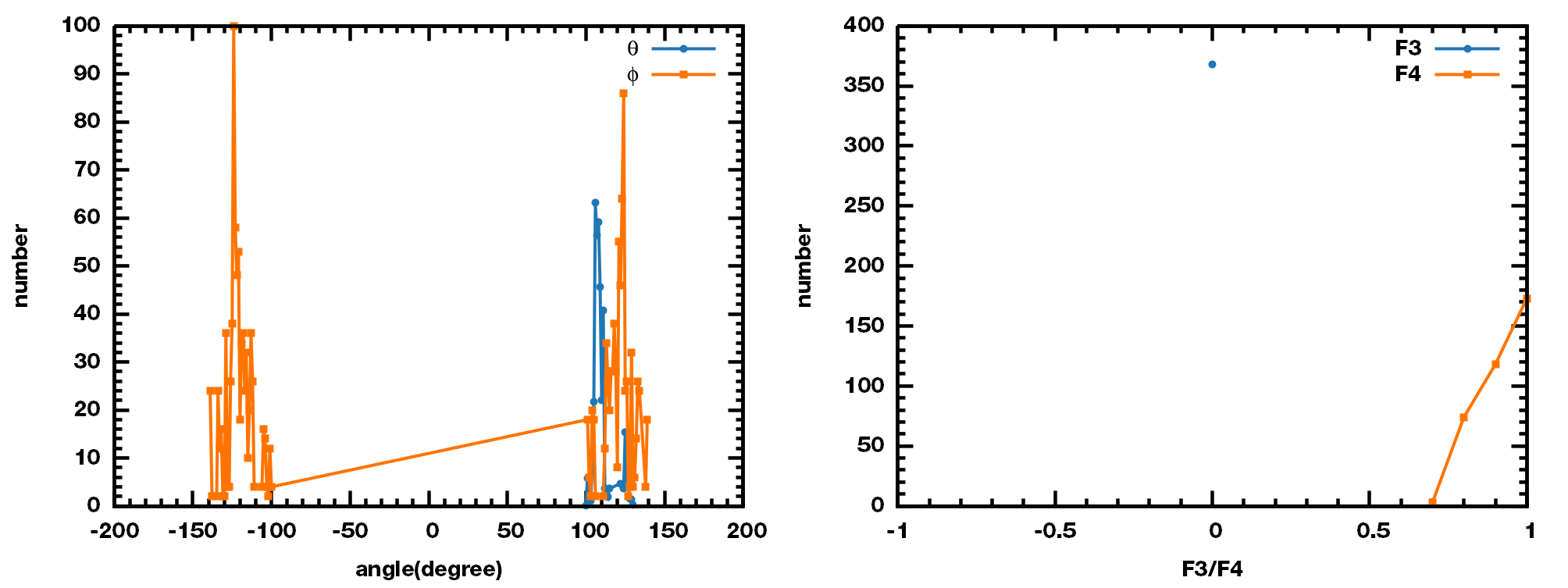
在此示例中, 每帧构型中氧原子的数目为1610, 水分子的总原子数目为6440. 在测试机器上(操作系统: Windows10; 内存: 8GB; 处理器:Inter(R) Core(TM)i5-7400 CPU @3.0GHZ), 脚本处理一帧构型所需的时间为5分钟, 而Fortran代码仅需1秒左右. 可以看出Fortran的计算速度远远高于脚本.
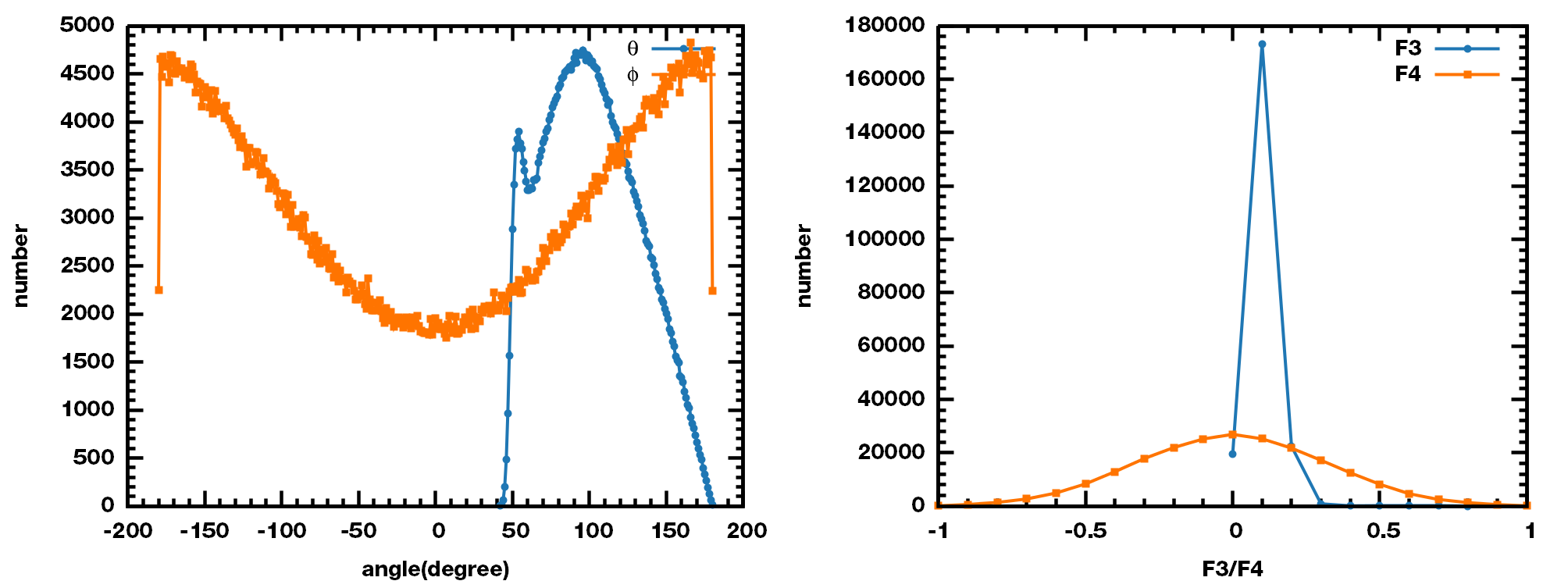
示例5: 甲烷水合物模拟
在水合物计算相关的文章中, 通常根据F3/F4随时间的变化规律的来分析水合物的生成过程. 在此, 我们建立如下图所示的初始结构, 盒子左边为2×2×2的甲烷水合物晶胞, 右边为甲烷-水混合溶液.
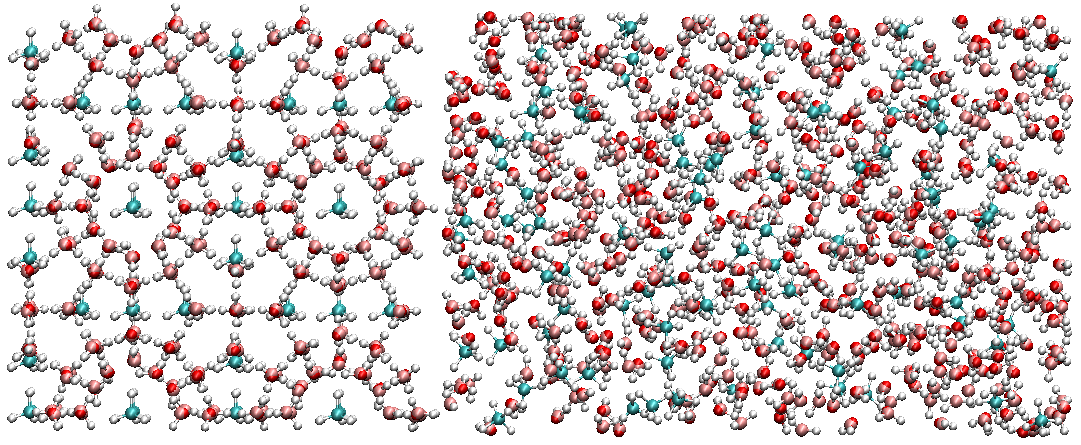
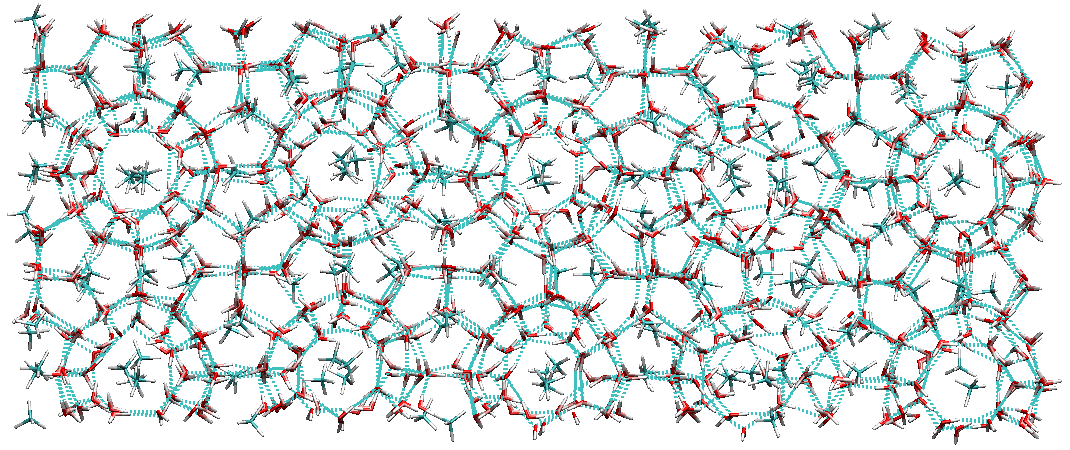
依次进行EM, NVT, NPT和80 ns的MD模拟, 水合物的最终结构如下图.
计算得到水合物生成过程中F3/F4的变化如下图.
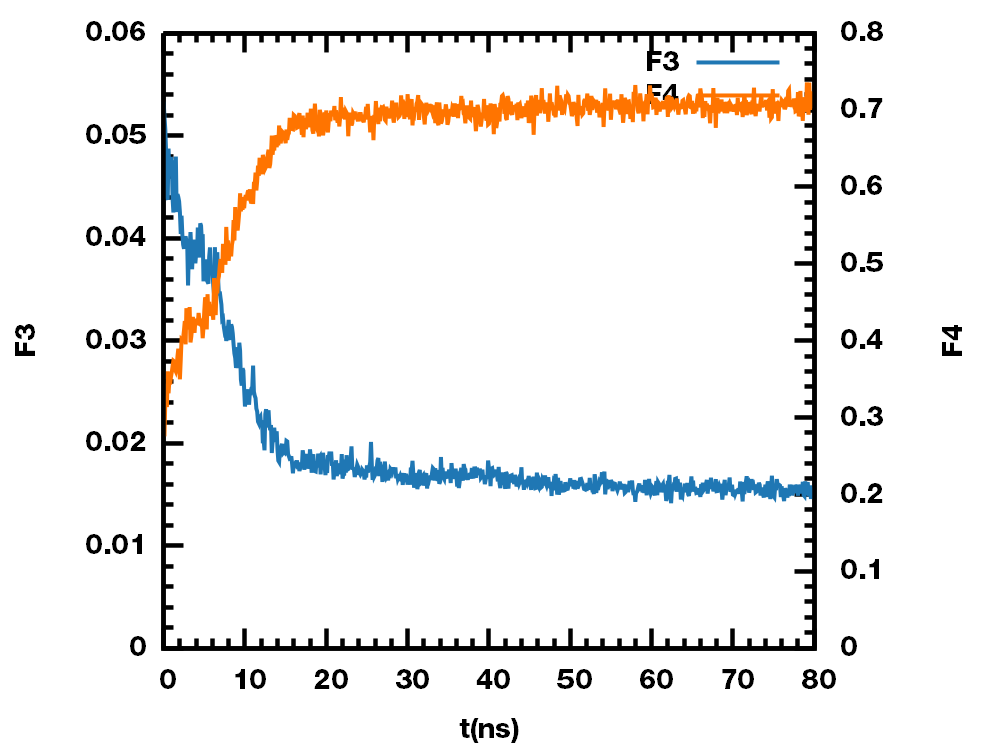
可以看出, 代码的计算结果与文献一致, 当水合物生成以后, 对应的F3值接近0.01, F4值接近0.7.
$\q$, $\f$, F3和F4的分布如下
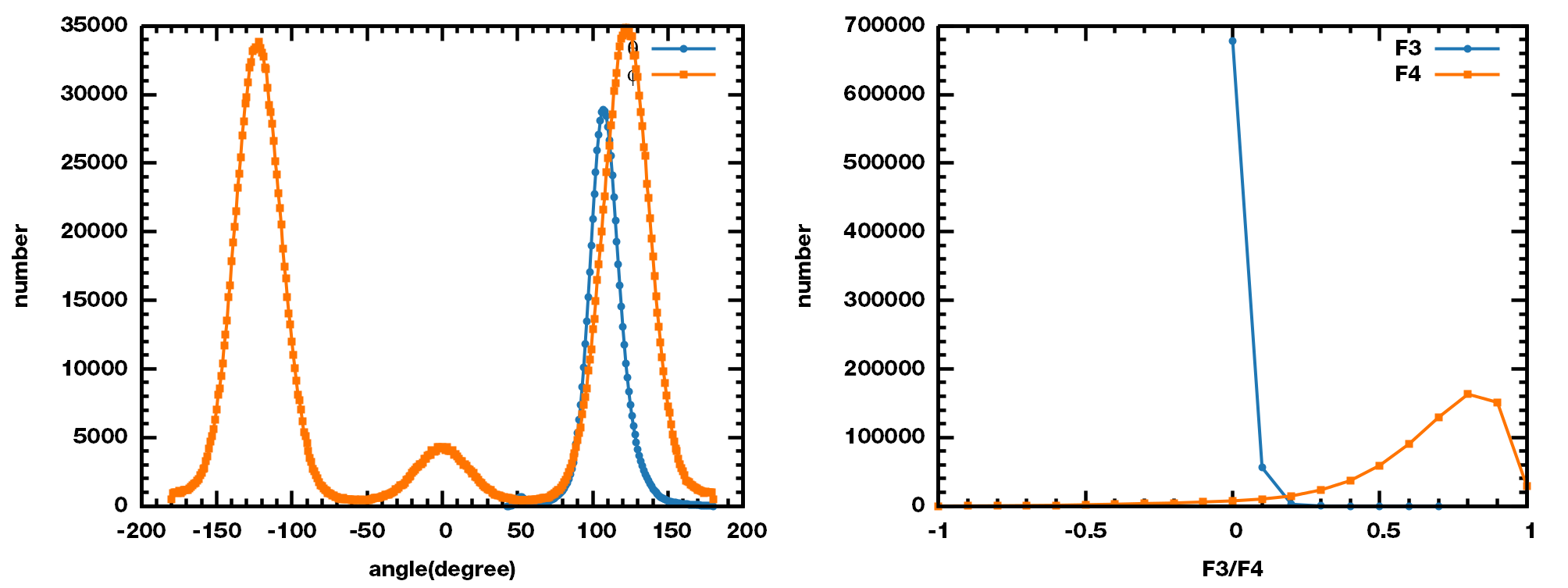
再快一些
我们使用Fortran处理gro文件时, 需要先进行一步转换步骤, 当轨迹很大时, 得到的gro文件会变得更大. 要想计算速度更快一些, 那么我们可以考虑直接处理xtc轨迹文件. 为此, 我们需要使用GROMACS提供的XTC库.
可惜这里留给我空白太少了, 只得作罢.
更进一步
如果你使用C/C++完成了上面的处理程序, 那么你可以更进一步, 将其直接集成到GROMACS的源代码中, 称为GROMACS的一个内置工具, 像GROMACS自带的其他工具一样. 这样你重新编译后就可以直接gmx aop得到计算结果了.
如果你确定自己的代码没有问题, 那么可以将其发送给GROMACS开发人员, 让他们将其合并到新版本的发布中, 这样会有更多人受益的.
具体流程可以参考GROMACS团簇分析代码.
题外的话
-
在前面的定义中, 中心水分子氧原子周围其他水分子氧原子的数目和编号都不是确定的, 因而要计算的角度的数目也是不确定的. 这样我们就必须一帧一帧的处理, 需要使用
gmx select动态地选取所需的水分子, 而不能使用固定的编号列表. 如果我们改变一下定义, 计算时只考虑距离中心水分子氧原子最近的4个其他水分子氧原子所组成的角度(实际上, 有些论文中的AOP/F3序参数就是这样定义的, 前面定义中所用的距离截断距离3.5Å, 来自SPC水模型的RDF峰值. 其对应的配位数大致是4), 那计算流程就可以简化一些. 因为我们可以先使用gmx trjorder, 按照距离对中心氧原子周围的其他水分子进行排序, 这样我们所需要的4个其他氧原子编号就是固定的2 3 4 5, 从而要计算的角度的编号三联对也使固定的. 这样我们就不需要再使用gmx select, 也不需要自己写代码生成角度编号三联对了. -
如果我们需要计算处于不同盒子位置的氧原子的序参数, 用以表征界面的位置, 那我们需要输出每个中心氧原子的位置.
-
我们可以将F3, F4输出到相应PDB文件的占据数列和温度因子列, 这样就可以直接使用VMD等可视化程序对每个水分子按照其相应的F3或F4进行着色了. 对PDB进行简单的处理也可以得到每个时刻不同位置水分子的序参数, 因为可以很容易地计算界面位置.

-
如果你的轨迹是由其他程序生成的, 那你可以先将其转换为
.gro格式的轨迹. 你可以使用VMD进行转换, 也可以自己写脚本或程序进行转换.
参考文献
- Fengfeng Gao, Krishna M. Gupta, Shiling Yuan, Jianwen Jiang; Molecular Simulation 44(15):1220-1228, 2018; 10.1080/08927022.2018.1478090
平方/未知: 固态水 0.01, 液态水 0.1 - S. Alireza Bagherzadeh, Peter Englezos, Saman Alavi, John A. Ripmeester; J. Phys. Chem. B 116(10):3188-3197, 2012; 10.1021/jp2086544
平方/平均/错误角度: 固态水 0.0, 液态水 0.1 - Luis A. Báez, Paulette Clancy; Ann NY Acad Sci 715(1 Natural Gas H):177-186, 1994; 10.1111/j.1749-6632.1994.tb38833.x
平方/未平均: 冰 0, 固态水 0.02 - Stewart K. Reed, Robin E. Westacott; Phys. Chem. Chem. Phys. 10(31):4614, 2008; 10.1039/b801220b
平方/平均: 固态水 0.01, 液态水 0.1 - Yen-tien Tung, Li-jen Chen, Yan-ping Chen, Shiang-tai Lin; J. Phys. Chem. C 115(15):7504-7515, 2011; 10.1021/jp112205x
平方/未平均: 冰 0, 水合物 0.1, 液态水 0.8, 界面 0.4 - Felipe Jiménez-ángeles, Abbas Firoozabadi; J. Phys. Chem. C 118(21):11310-11318, 2014; 10.1021/jp5002012
平方/平均: - P.m. Rodger, T.r. Forester, W. Smith; Fluid Phase Equilibria 116(1-2):326-332, 1996; 10.1016/0378-3812(95)02903-6
未平方/平均/10倍: 水合物 0.1, 液态水 0.9 - Kyle Wm. Hall, Sheelagh Carpendale, Peter G. Kusalik; Proc Natl Acad Sci USA 113(43):12041-12046, 2016; 10.1073/pnas.1610437113
- Bjørn Steen Sæthre, Alex C. Hoffmann, David Van Der Spoel; J. Chem. Theory Comput. 10(12):5606-5615, 2014; 10.1021/ct500459x
- Jyun-yi Wu, Li-jen Chen, Yan-ping Chen, Shiang-tai Lin; Phys. Chem. Chem. Phys. 18(15):9935-9947, 2016; 10.1039/c5cp06419h
平方/平均: 冰 0, 水合物 0.1, 液态水 0.8 - C. Moon, R. W. Hawtin, P. Mark Rodger; Faraday Discuss. 136:367, 2007; 10.1039/b618194p
未知: 固态水 0.01, 液态水 0.1 - Qibin Li, Qizhong Tang, Tiefeng Peng, …, Chao Liu, Xiaoyang Shi; Int. J. Mod. Phys. B 29(27):1550185, 2015; 10.1142/S0217979215501854
平方/平均/错误角度: 冰 0, 液态水 0.1
