- 原文Program RING
- 翻译整理: 于桐桐; 校对: 李继存
- 2022-02-22 21:25:32
RING是一个坐标转换程序, 可以为解释环的构象和平面环的形式提供定量的数据. 根据对N元环的简正分析可以知道, 存在N-3个振动描述面外的褶皱, 2N-3个振动描述面内的变形. 根据这一分析, 读取环形分子的笛卡尔坐标后, RING将提供如下信息:
- 环褶皱坐标
- 环变形坐标
- 环取代基方向(轴向、赤道等)
- 平均平面和最小二乘平面的方向
环分子的构象和电子结构分析需要这些信息:
- 描述特定褶皱物的非平面构象
- 用基本构象表示给定的环构象
- 描述构象过程, 如环的赝旋转、环反转等
- 描述构象能超面以及相关势能
- 以定量而非定性的方式确定取代基的位置
- 定量描述平面环相对于参考多边形的变形
- 描述平面环分子键的赝旋转和其他动力学过程, 如键移位
- 定量描述环取代基效应的
- 定量描述分子中的开环过程
相关文献
A) 理论
- A1) A General Definition of Ring Puckering Coordinates, D. Cremer and J.A. Pople, J. Am. Chem. Soc. 97, 1354-1358 (1975).
- A2) RING - A Coordinate Transformation Program for Evaluating the Degree and Type of Puckering of a Ring Compound, D. Cremer, Quantum Chemical Program Exchange, No. 288, 1-8 (1975).
- A3) A General Definition of Ring Substituent Positions, D. Cremer, in “Stereochemistry and Conformational Analysis”, Israel J. Chem. 20, 12-19 (1980).
- A4) On the Relationship between the Mean Plane and the Least-Squares Plane of an N-membered Puckered Ring, H. Essen and D. Cremer, Acta Cryst. B40, 418-420 (1984).
- A5) On the Correct Usage of the Cremer-Pople Puckering Parameters as Quantitative Descriptors of Ring Shapes - A Reply to Recent Criticism by Petit, Dillen, and Geise, D. Cremer, Acta Cryst. B40, 498-500 (1984).
- A6) Calculation of Puckered Rings with Analytical Gradients, D. Cremer, J. Phys. Chem. 94, 5502 (1990).
B) 应用
- B1) Molecular Orbital Theory of the Electronic Structure of Organic Compounds. 23. Pseudorotation in Saturated Five-Membered Ring Compounds, D. Cremer and J.A. Pople, J. Am. Chem. Soc. 97, 1358-1367 (1975).
- B2) Theoretical Determination of Molecular Structure and Conformation. 3. The Pseudorotation Surface of 1,2,3-Trioxolane and 1,2,4-Trioxolane, D. Cremer, J. Chem. Phys. 70, 1898-1910 (1979).
- B3) Theoretical Determination of Molecular Structure and Conformation. 4. Electronic Effects Influencing the Stability of Methyl Substituted Primary Ozonides, D. Cremer, J. Chem. Phys. 70, 1911-1927 (1979).
- B4) Theoretical Determination of Molecular Structure and Conformation. 5. Electronic Effects Influencing the Stability of Methyl Substituted Final Ozonides D. Cremer, J. Chem. Phys. 70, 1928-1936 (1979).
- B5) Theoretical Determination of Molecular Structure and Conformation. 11. The Puckering of Oxolanes, D. Cremer, in “Application of Theory to Organic and Organo-metallic Molecules”, Israel J. Chem. 23, 72-84 (1983).
- B6) Theoretical Determination of Molecular Structure and Conformation. 12. Puckering of 1,3,5-Cycloheptatriene, 1H-Azepine, Oxepine, and their Norcaradienic Valence Tautomers, D. Cremer, B. Dick, and D. Christen J. Mol. Struct. 110, 227-291 (1984).
C) 综述
- C1) Ab initio Studies of Six-Membered Rings, Present Status and Future Developments, D. Cremer and K.J. Szabó, Methods in Stereochemical Analysis, Conformational Behavior of Six-Membered Rings, Analysis, Dynamics, and Stereoelectronic Effects, E. Juaristi, Editor, VCH Publishers, 1995, p. 59.
A) 环褶皱:描述N元环的非平面构象
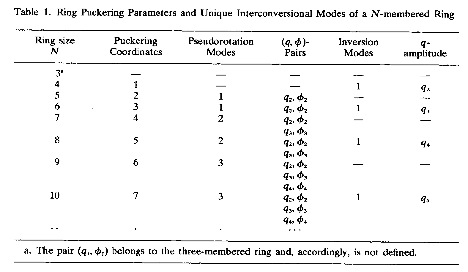
对于一组振幅有限的$N-3$个面外振动, 可以精确地指定一个褶皱环, 振动振幅对应于N个面外坐标$z_j$, 可以由褶皱方程(1)和(2)精确地指定. [A1,A6,C1]
\[╤ z_j &=({2/N})^½ ∑_{n=2}^{(N-2)/2}q_n \cos[φ_n+2n(j-1)/N]+({1/N})^½q_{N/2}(-1)^{j-1} □&N为偶数 \tag{1} \\ z_j &=({2/N})^½ ∑_{n=2}^{(N-1)/2}q_n \cos[φ_n+2n(j-1)/N] □&N为奇数 \tag{2} ╧\]其中, $q_n$对应褶皱振幅, $φ_n$表示赝旋转相位角, 索引$n$表示N元环的赝旋转模式. 推导褶皱坐标时, $n = 0$和$n = 1$分别对应平面参考环在平均平面上的平移和整体旋转[C1]. 三元环必定是一个平面, 不存在任何面外振动, 因此, 索引只有$n=0$和$n=1$两种情形, 分别定义了平移参数$q_1$和旋转角度$φ_1$. 褶皱从4元环开始(N-3=1:褶皱幅度$q_2$, 面外振动导致“冠状褶皱”), 赝旋转从5元环开始(N-3=2:褶皱幅度$q_2$, 赝旋转相位角$φ_2$). 对于一个完整的赝旋转周期, 相位角2从0°增大到180°, 再增加到360°, 360°的状态与0°完全相同, 对五元环来说, 这样的赝旋转周期如图1所示. [A1,A3,B2,B3]
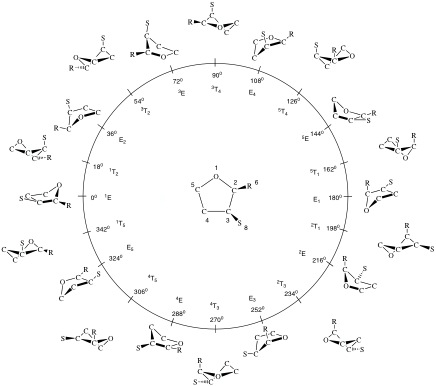
图1 四氢呋喃的赝旋转周期(O为1号原子, 沿环顺时针编号). 根据环构象的规律(见下文), $φ_2=0°$时, 对应O原子位于环顶端, 具有Cs-对称性的信封型构象;$φ_2=90°$时, 对应具有C2对称性的扭转构象. 图中展示了沿赝旋转周期($0°≤φ_2≤360°$)的10个信封型(E)构象和10个扭转(T)构象, 它们具有固定褶皱振幅$q_2$. 在赝旋转周期的中心位置是$q_2 = 0 Å$的平面形式. 沿赝旋转周期存在无数种形式, 其中只显示了20种E和T型构象, 它们的O原子处于五元环上的不同位置. 符号前面的上标对E形式表示顶点原子处于平均平面之上, E后面的下标表示顶点原子处于平均平面之下. 对于T型构象, 前面始终具有上标, 后面始终具有下标, 分别表示具有最大二面角的键两端的原子, 其中第一个原子处于平均平面上方, 第二个原子处于平均平面下方. 值得注意的是, $φ_2$值相差180°对应着原始形式和反转形式. 构象空间是N-3=2维的, 展示的取代基R和S用以说明赝旋转过程中不同的取代基取向.
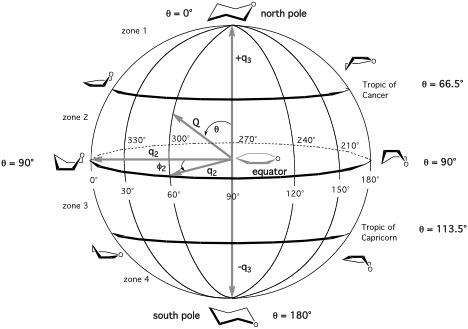
图2 褶皱六元吡喃环的构象球. 褶皱坐标$\{q_2, φ_2, q_3\}$张成了球面, 同时显示了一些明显的经纬度. 不同环型的位置沿赤道、北回归线和南回归线以30°的间隔显示(与图3比较). 为清晰起见, 只显示了构象球的正面, 球背面的构型如图3所示, 图中始终标注了O1原子.
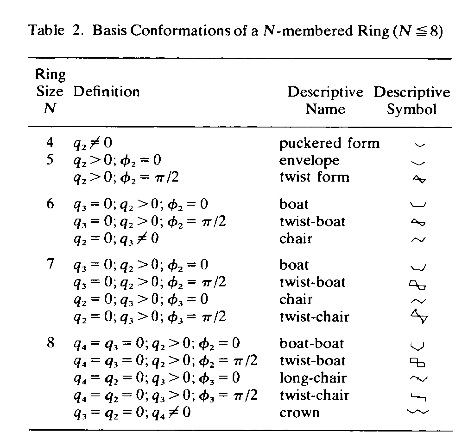
六元环 如环己烷, 具有6-3=3个褶皱坐标, 可以分成赝旋转坐标组$\{q_2, φ_2\}$, 描述船式和扭转船式的赝旋转, 单个冠褶皱幅度$q_3$, 描述椅式($q_3>0$), 反转椅式($q_3<0$). 对于赝旋转周期, 褶皱幅度始终为正.
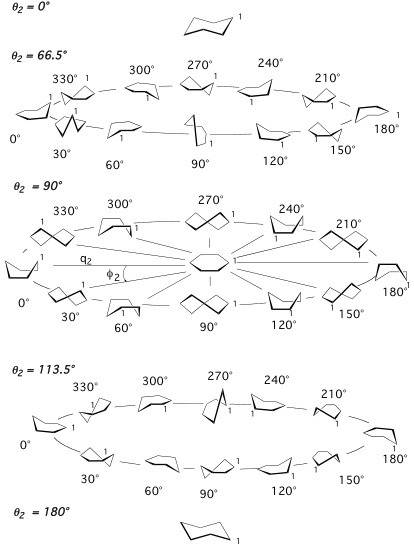
图3 褶皱环己烷的构象. 展示了超球面角度$θ_2$=66.5°、90°和113.5°处的三个赝旋转周期(与图2比较). 不同环型沿赤道、北回归线和南回归线以30°的间隔依次显示(与图2比较).
非平面 七元环 有7-3=4个褶皱参数, 张成两个不同的赝旋转空间$\{q2, φ_2\}$和$\{q_3, φ_3\}$. 构象能量空间是四维的, 其单位向量相互正交, 给出了7元环船形、扭舟形、椅形和扭椅形的位置. 构象空间可以用图4所示的环面来表示.
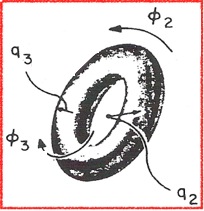
图4 以环面表示的7元环的赝旋转周期.
在八元环中, 存在这两个赝旋转空间, 以及一个由褶皱幅度$q_4$所张成的额外的冠褶皱空间.
对于偶元环, 一般存在$(n- 4)/2$个赝旋转模式, 每个由褶皱幅度-相位角对$\{q_n, φ_n\}$描述, 其中$n = 2,3, …(n - 2)/2$. 此外, 对于偶元环, 还有一个额外的褶皱幅度$q_{N/2}$, 用以描述冠折叠(N = 4: 环的折叠;N = 6: 椅式褶皱, N = 8、10等: 冠褶皱).
对于奇元环, 一般存在$(n-3)/2$个赝旋转模式, 每个模式同样由褶皱幅度-相位角对$\{q_n, φ_n\}$描述, 其中$n = 2,3, …(n - 1) / 2$. 所有环构象都对应于(N-3)维构象能量空间中的点.
出于分析的原因, 球(N = 6)或超球(N > 6)褶皱坐标$\{Q, Θ_n, φ_n\}$比上述超柱坐标$\{q_n,φ_n\}$更有用. 为此, 我们定义了总褶皱幅度$Q$和极角$Θ_n$(见图2和图3中的六元环). [A1,A3]RING程序可以计算它们.
在表1(取自[A3])中, 根据环的大小列出来褶皱坐标.
平面环适合作为褶皱环的参考, 它位于一个平面上, 被称作平均平面($z_j=0$), 存在惟一的数学算法来确定平均平面, 具体参见[A1,A6]. 每个褶皱环可以投影到平均平面, 得到一个与其关联的平面环. 投影平面环用一组2N-3个变形参数描述, 它们量化了该平面环与具有单位长度的正N元多边形的偏差.
基构象的定义:与张成N元环构象空间类似, 褶皱坐标也定义了基构象, 它们可视为构象空间的基向量. 为此, 褶皱幅度被固定为一个常数值(大于零), 相位角的值如表2所定义. 在构象分析中, 对一些具有高对称性的褶皱环形式, 已经给出了常用名称, 这些名称反映了褶皱环的形式. 其中一些形式被证明是基构象(表2), 而另一些则被发现是处于赝旋转周期和反转路径之间的半反转路径上. 这样可以通过构象空间的连接路径将褶皱环的形式相互联系起来, 从而简化构象分析.
B) 环变形:描述平面N-元环的变形
C)环取代基:描述环取代基的取向
一旦确定了褶皱环的平均平面, 就可以确定取代键相对于这个平面的方向. 那些几乎垂直于平均平面的键被称为“g-轴向键”(g代表几何), 而那些几乎平行于平均平面的键称为“g-赤道键”[A3]. 既不是g轴向, 也不是g赤道, 而是处于中间的取代键取向, 称为“g斜”(相对于平均平面倾斜). 这些定义将环己烷中C-H键的Barton-Hassel-Pitzer-Prelog规则推广到了所有环上.
RING程序计算了参数$α$和$β$, 它们给出取代键的方向, 如图1所示. 当然, 同样的描述也可以用在环键上.
区分环的顶(top)面和底(bottom)面是有用的. 应用规则对环进行编号时, 每个原子都会有相应的序号, 如果察看时, 环上的原子序号沿顺时针方向增加, 则观察到的是环的顶部, 反之则为环的底部.
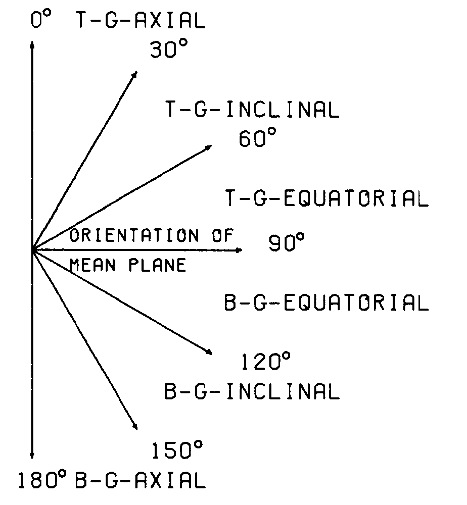
图5 相对于环平均平面的取代基取向的定义
