- 2025-06-03 21:56:53
问题
在复杂电解质溶液体系中, 带电表面附近会形成双电层, 空间中离子分布不均匀, 导致相应离子和水分子在不同空间区域的迁移性质不同, 如扩散系数. 空间中离子和水分子扩散系数的不同会使带电表面不同距离处的性质不同, 因而计算双电层附近离子或水分子的扩散系数随距离的变化有助于分析双电层的结构.
分析
更广义地说, 类似上面问题中的这种区域相关的性质分析是很常见的. 理论上任何具有局域性的性质都可以进行相应的分析, 获知其在不同区域的分布情况, 最简单的例子就是不同区域的密度或浓度分布. 这种分析不常见的一个可能原因在于过程稍复杂, 不是一个简单命令就能完成的, 需要根据自己的目的或要计算的性质进行较多的设置.
局域性质分析的难点在于, 同一区域中要分析的分子编号在不同时刻很可能是不同的, 同一分子在不同时刻很可能处于不同区域. 从区域的角度看, 模拟过程中同一区域内的分子可以动态交换, 没有固定的编号; 从分子的角度看, 同一分子在某一时刻处于此区域, 在另一时刻又会处于另一区域. 这就导致我们无法简单地抽取轨迹并进行分析.
局域性质分析的一个示例是我很早之前写过的滞留时间计算. 流程与一般的局域性质分析大致类似, 但只需要统计轨迹的时间起始点, 不需要抽取相应的轨迹并进行分析, 所以还算简单.
使用GMX自带的工具分析离子或者水分子整体的扩散系数很简单, 但要计算模拟过程中不同区域的离子或者水分子的扩散系数则必须抽取轨迹并处理后才能得到, 所以步骤更多, 思考链也比较长.
这里我给出一个示例, 如何基于GMX自带的工具, 借助脚本完成局域扩散系数的计算. 这个流程对于任意局域性质分析都是适用的, 只不过要对脚本进行适当的修改.
示例
使用GMX自带的spc216.gro作为示例体系.
准备模拟文件
我们要对两个体系进行模拟, 一个是满的水盒子中的体相水(bulk), 一个是块体水(slab). 前者用于计算体相水的扩散系数, 作为后者的对比.
体相水使用原来的盒子就可以了
初始盒子原点处于体系中心处, 这样情况下沿z方向扩展成块体构型时不很方便, 所以先将所有原子置于盒子中, 同时将盒子z方向长度扩大为原来的3倍:
gmx editconf -f spc216.gro -c -box 1.86206 1.86206 5.58618 -o conf.gro
这样我们就有了块体水的初始构型.
准备topol.top很简单, 我们就使用刚性SPCE水模型吧, 这样氧原子的扩散系数和水分子的是一样的.
准备grompp.mdp文件时注意, 由于盒子较小, 需要修改下面3个截断值为0.9:
rlist = .9 ; 邻区列表截断距离(nm)
rvdw = .9 ; 范德华截断半径
rcoulomb = .9 ; 静电截断半径, 不超过最小盒子边长一半
模拟
因体系简单, 且初始结构较好, 我们忽略NPT预平衡过程, 直接进行2 ns的NVT模拟, 轨迹坐标保存时间间隔取.2 ps, 前1 ns作为预平衡, 后1 ns作为成品模拟用以分析扩散系数.
处理轨迹
PBC/时间修正
抽取最后1 ns轨迹备用. 为了后面便于分析和查看, 可以对轨迹进行PBC处理, 并修正时间起点为0
gmx trjconv -f traj_comp.xtc -b 1000 -pbc whole -t0 0 -o traj.xtc
> 0
坐标对齐
理论上, 进行区域分析需要基于一套固定的坐标系, 类似经典力学中作为背景的绝对坐标系. 如果我们的体系没有使用PBC, 或者体系中存在固定不动的参考物(比如, 我们在盒子中放置一层冻结的膜), 那直接使用体系所用的坐标系统即可. 在我们的示例中, 这两个条件都不满足. 由于存在PBC, 块体水沿z方向移动不会对模拟产生任何影响. 但如果体系存在沿z方向的显著移动, 直接使用z坐标分析z方向的局域性质时就必须进行坐标对齐, 否则得到的结果就是整个块体水的平均值, 无法反映性质对z坐标的依赖关系.
坐标对齐的关键是弄清楚局域性质所依赖的变量是什么. 在块体的情况下, 容易想到, 我们实际关心的是性质随距中心或表面距离的变化关系, 因此, 选择对齐坐标时有两种方法: 块体中心和表面. 问题在于这两种参考点在模拟所用的原始坐标系中并不是固定不变的, 也可能会发生显著的移动, 特别是如果运行模拟时没有进行质心运动移除或移除频率太低. 这就是我们需要进行坐标对齐的原因. 对齐后可以保证块体中心或表面的坐标始终固定, 这样后面的分析就是基于对齐后固定的坐标系, 容易处理了.
坐标对齐一般需要对轨迹中的每帧结构进行坐标调整, 并且需要有比较稳健的确定对齐点的方法, 因此操作麻烦. 对于我们的示例, 由于模拟时间较短, 且每步都进行了质心运动移除, 块体中心移动的影响很小, 所以我们不进行坐标对齐了, 直接使用原始盒子坐标.
分析
整体扩散系数
先分别计算体相水与块体水中所有氧原子的扩散系数
- 创建所有氧原子的索引文件
gmx make_ndx -f conf.gro
> a OW
> q- 计算msd
gmx msd -f traj.xtc -s -n -o
> 3- 绘制MSD图
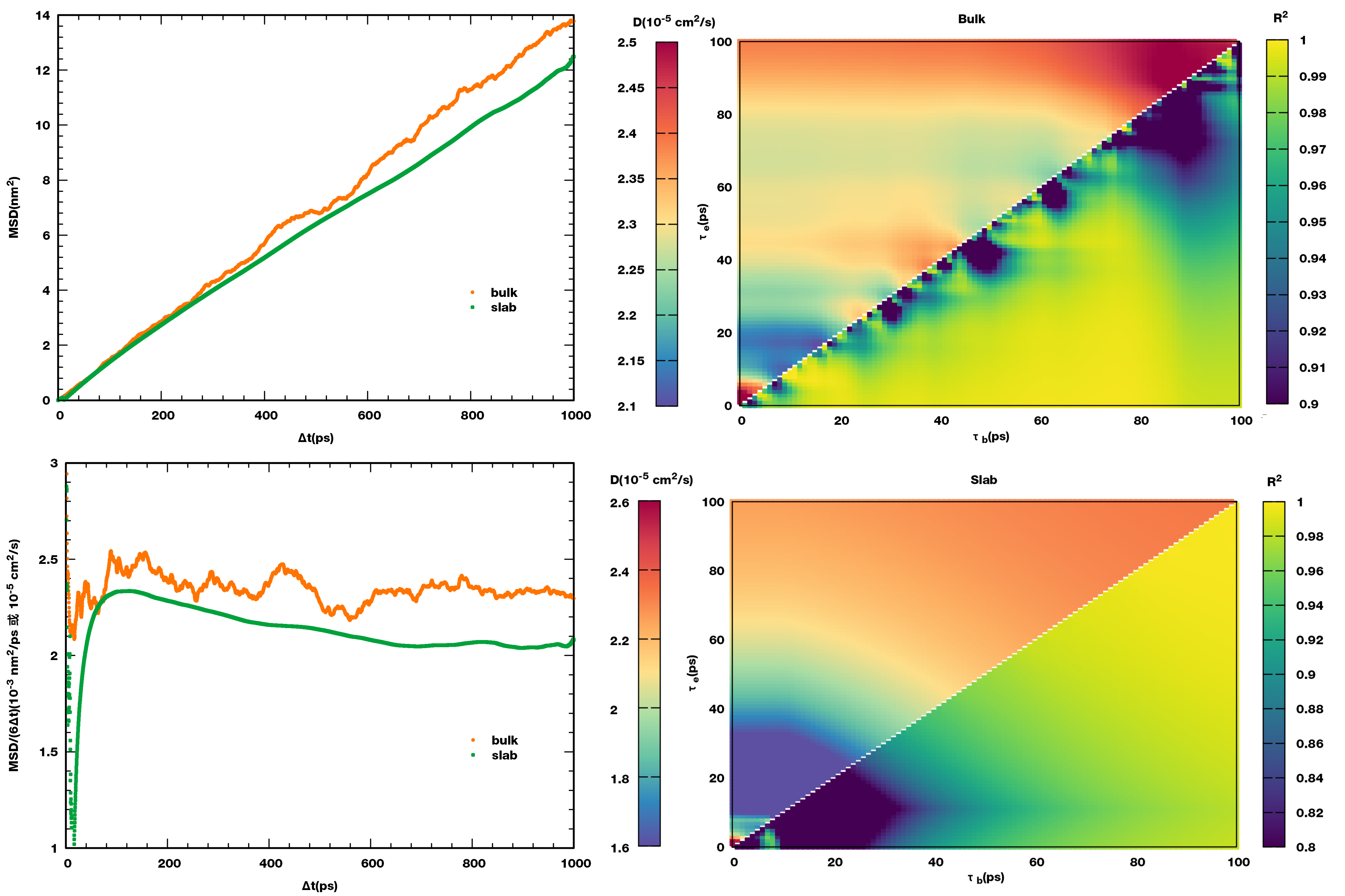为计算扩散系数, 我们需要拟合$MSD(τ)=6Dτ$. 如何确定拟合的起止时间是拟合的关键. 除了借助上面的滑动扩散系数外, 这里我们测试一下扫描的方法, 以一定步长改变拟合的起始时间, 终止时间, 并进行拟合, 得到扩散系数以及拟合曲线的R²(也可以使用其他表征拟合好坏的量), 最后将这两个量绘制在同一填色图上.
虽然模拟时间较短, MSD曲线看起来还可以, 但滑动扩散系数曲线看起来收敛不够好, 特别是块体水的. 此外, 整个模拟时间内块体水的扩散系数都小于体相水的, 这也出乎意料. 具体原因待考.
密度剖面
在分析氧原子的局域扩散系数前, 我们先分析一下氧原子沿z方向的密度分布. 查看密度剖面, 有两个原因:
- 确认体系沿z方向是否有明显的移动
- 确定z区间的范围, 以便确定如何划分
gmx density -f traj.xtc -n
> 3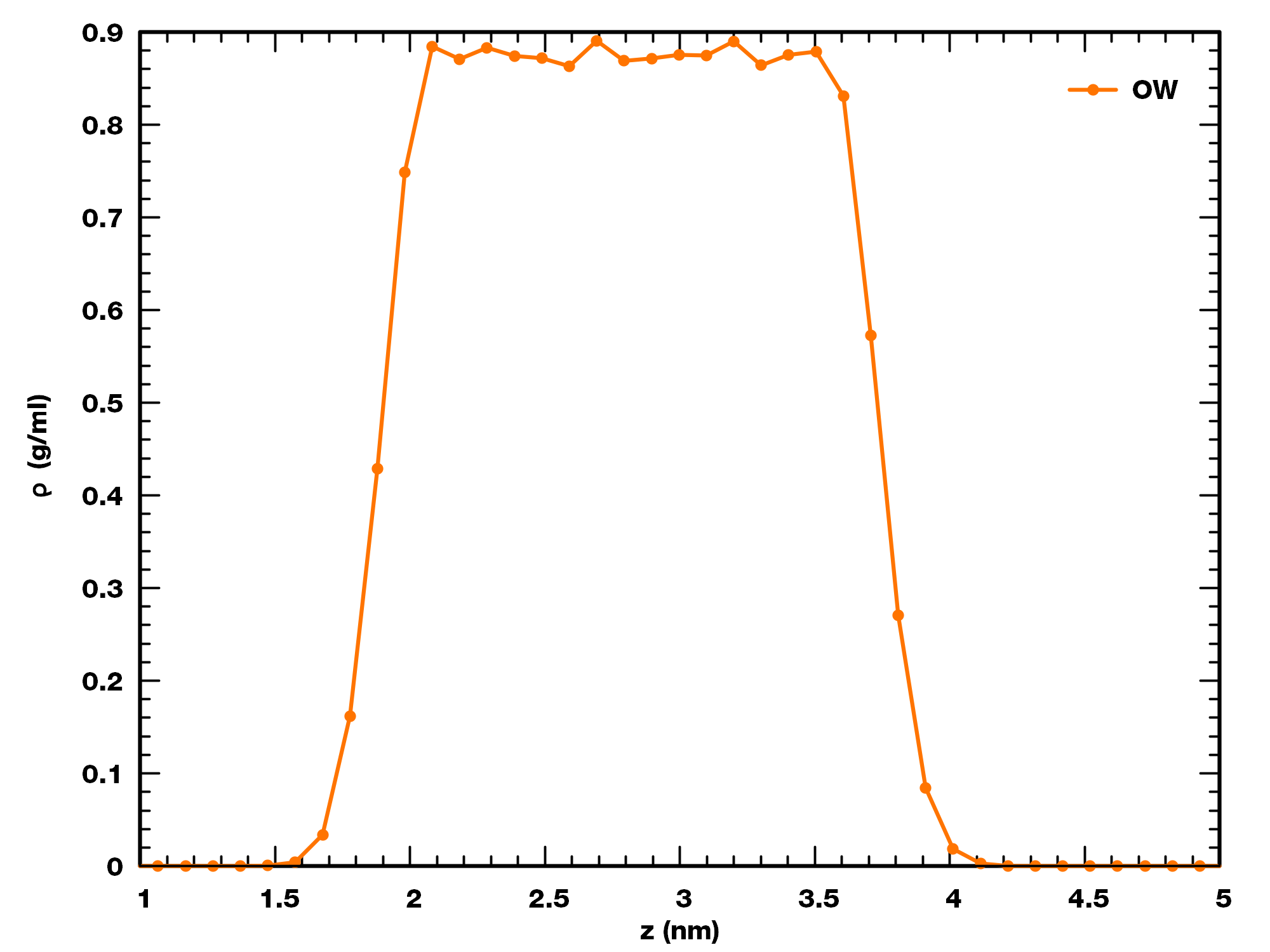
从密度剖面可以看出, 氧原子的分布范围为 1.5-4.1 nm. 据此, 我们取盒子z方向分格间距为 0.5 nm. 注意, 此分格间距数值的选取应根据盒子z方向的长度, 轨迹的保存频率, 待分析物质的扩散快慢综合考虑. 这里使用 0.5 nm仅为示例.
分析局域扩散系数
要分析局域扩散系数, 可以先将每个离子或分子的轨迹单独抽取出来, 再根据其z坐标将轨迹分成多个片段, 分别计算每段轨迹中离子或分子的MSD, 并对z区间进行平均, 最后根据每个z区间的平均MSD拟合扩散系数.
要分析OW在不同z坐标处的扩散系数, 所用步骤如下:
- 抽取每个
OW的轨迹, 保存到单独的轨迹文件 - 创建只含单个
OW的tpr文件 - 将每条
OW轨迹, 根据z坐标切分成多段 - 计算每段子轨迹的MSD
- 平均每个z区间的MSD
- 根据每个z区间的MSD拟合其扩散系数
流程
抽取每个OW的轨迹
先将每个OW保存为单独的组
gmx make_ndx -f conf.gro -n -o OW.ndx
> splitat 3
> del 3
> del 2
> del 1
> del 0
> q再抽取对应的轨迹(注意索引文件中索引组的编号从0开始)
for i in {0..215}; do
echo $i | gmx trjconv -f traj.xtc -n OW.ndx -o OW-$i.xtc -quiet
done创建只含单个OW的tpr文件
gmx convert-tpr -s -n OW.ndx -o OW.tpr
> 0根据z坐标切分轨迹
这是局域性质分析的难点, 自己写代码处理不容易, 所以我们组合已有的GMX工具来完成:
- 对 GMX2019 版本, 借助
gmx trjconv -sub功能 - 对 GMX2023 版本, 借助
gmx extract-clusters -s功能
根据手册的说明, 使用该功能需要一个索引文件, 其中的每个索引组保存的并非原子编号, 而是轨迹帧编号(从1开始). 运行命令后, 会将每个组包含的帧抽取出来, 保存到单独的轨迹文件. 为此, 我们需要想办法生成需要的索引文件.
此索引文件的生成, 可以借助gmx cluster -dm -clid, 但需要自己创建xpm矩阵文件, 并不方便. 所以我们改为根据gmx select得到的信息自己写脚本生成.
计算轨迹片段的MSD
直接使用gmx msd命令即可
平均每个z区间的MSD
根据得到的msd数据, 自写脚本平均
根据每个z区间的MSD拟合其扩散系数
具体拟合区间仍要注意
简化流程
上面的流程步骤较多, 大致将每一步的操作都分解开来, 适合不太熟悉GMX的初学者测试或对比结果. 如果比较熟悉GMX的使用, 可以将上面的步骤简化.
我们不需要将切分轨迹, 使用原始轨迹即可, 计算msd时候, 我们需要指定的是要计算分子的索引号, 起止时间. 因此, 我们在分析gmx select结果时直接生成需要的数据即可.
结果
每个z区间内, 所有轨迹片段的MSD曲线以及平均MSD曲线
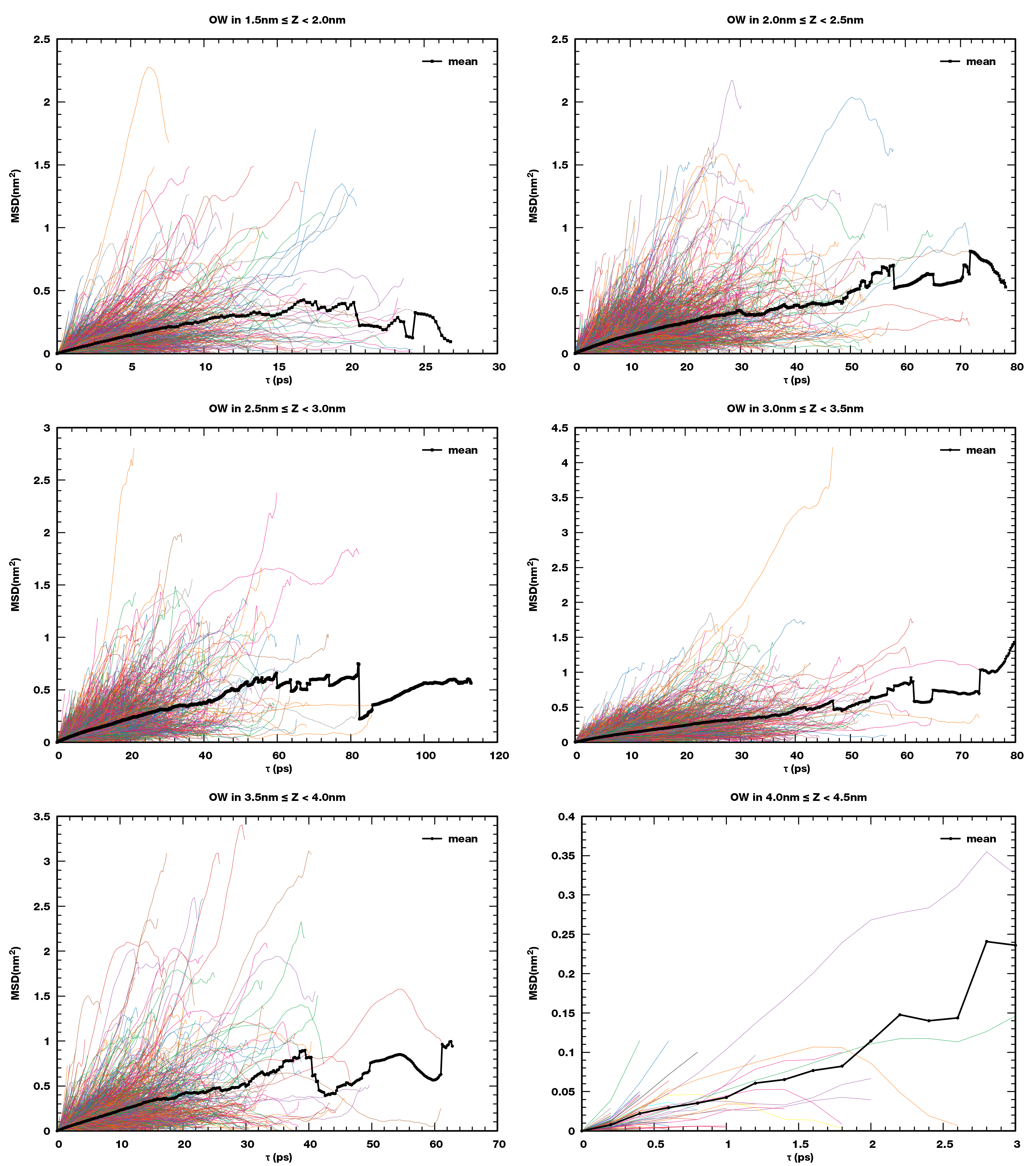
所有平均MSD曲线
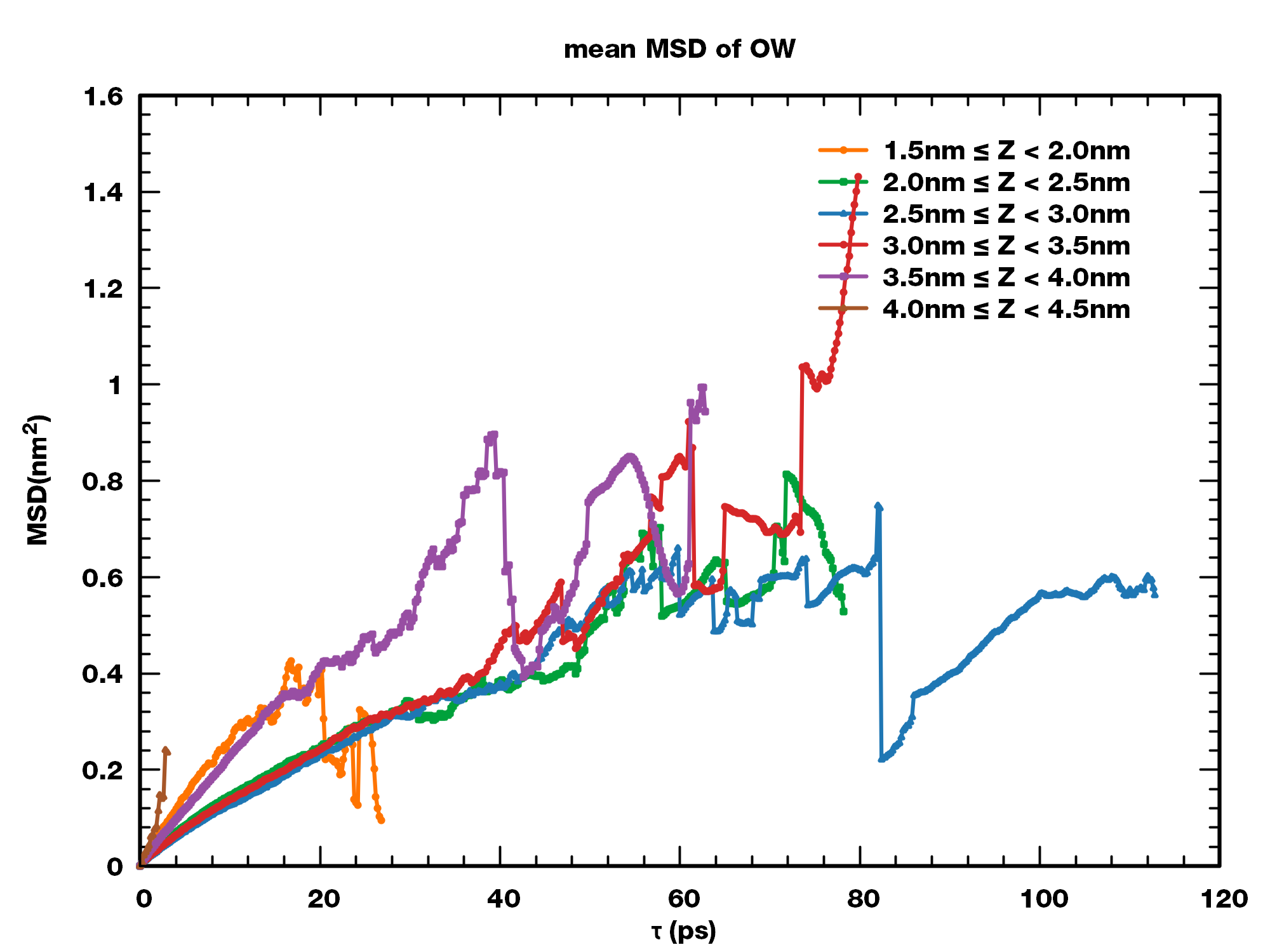
可以看到, 不同区间内的MSD曲线不同. 两个表面区间中的MSD曲线斜率明显大于体相区间的.
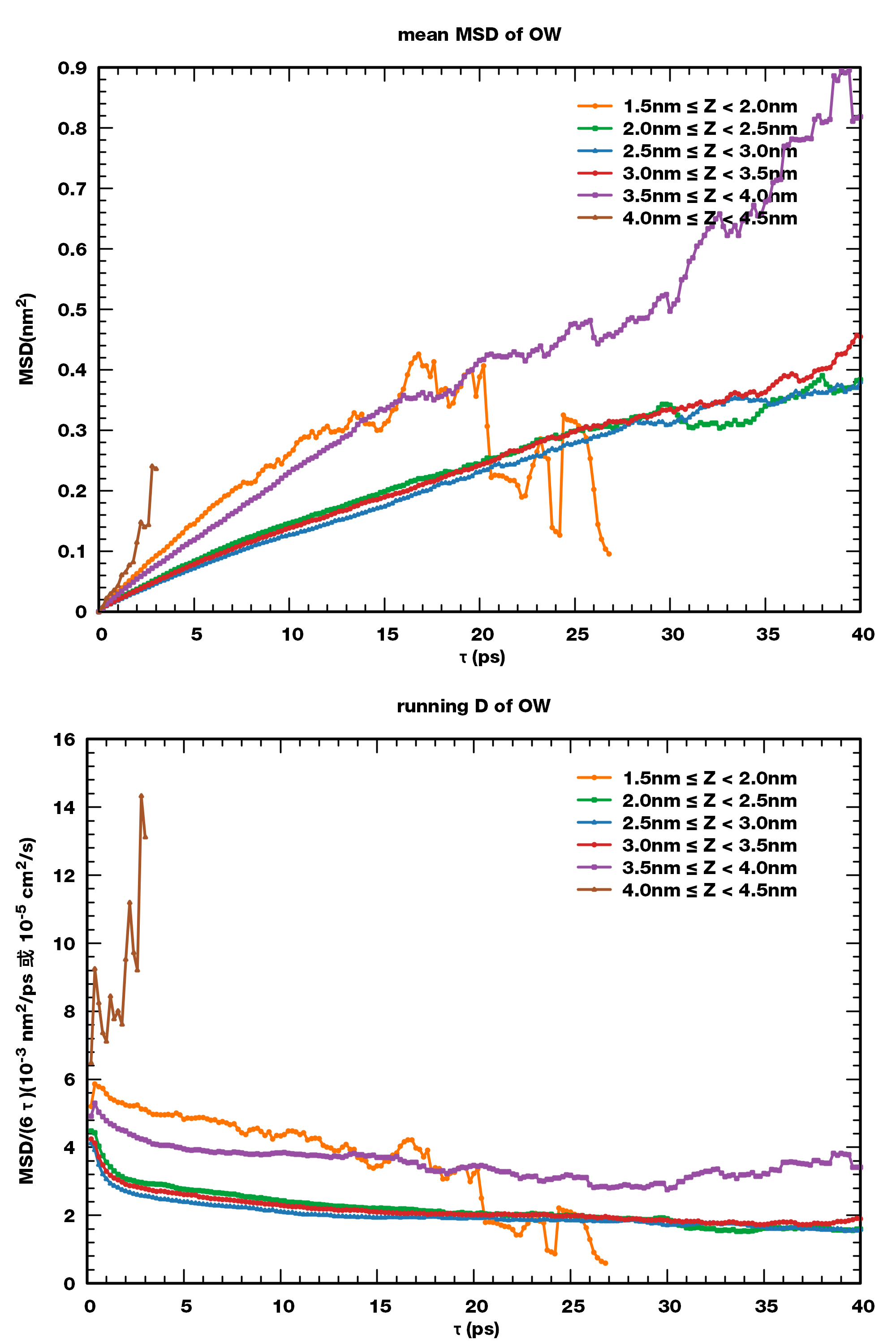
我没有仔细计算不同区间的扩散系数, 根据上图的结果显示, 表面层的扩散系数大致是体相层的2倍.
对于块体中水分子的扩散系数, 我们可以预期应从中心到表面逐渐增大.
未考虑的
gmx msd所给MSD数据没有误差, 考虑误差后拟合扩散系数更合适- 对于块体体系, 只考虑z方向的扩散系数可能更合适
