哲●科●文Jerkwin 类别 标签 链接 关于 订阅

GROMACS教程：使用GROMACS计算MM-PBSA结合自由能

类别: 科   标签: gmx   阅读次数:   版权: (CC) BY-NC-SA ✕

基础知识

在分子模拟领域, 准确计算结合自由能(binding free energy)仍然是一个挑战. 为此, 人们发展了许多方法. 论文自由能计算方法及其在生物大分子体系中的适用性问题对这些方法有一些总结, 可供参考. 王喜军在一篇文章杂谈自由能计算，PMF，伞形抽样，WHAM中对一些基本概念进行了讲解. 在这些方法中, 自由能微扰(FEP)与热力学积分(TI)都是比较准确的成熟方法, 但计算量很大, 不适用于生物大分子体系. MM-PBSA(Molecular Mechanics-Poisson Bolzmann Surface Area, 分子力学泊松玻尔兹曼表面积)是一种对MD轨迹进行后处理以估计结合自由能的方法, 计算时会将溶剂视为均匀的连续介质, 并基于力场和隐式的连续介质模型, 对平衡轨迹中的许多帧进行平均, 以考虑温度的影响. 尽管MM-PBSA方法的准确度不如FEP和TI, 但这种方法的计算量小, 在分子识别, 区分结合的强弱方面是一种有效的方法, 因此在生物分子模拟和药物筛选领域应用广泛, 并已经成功地用于许多结合自由能的计算.

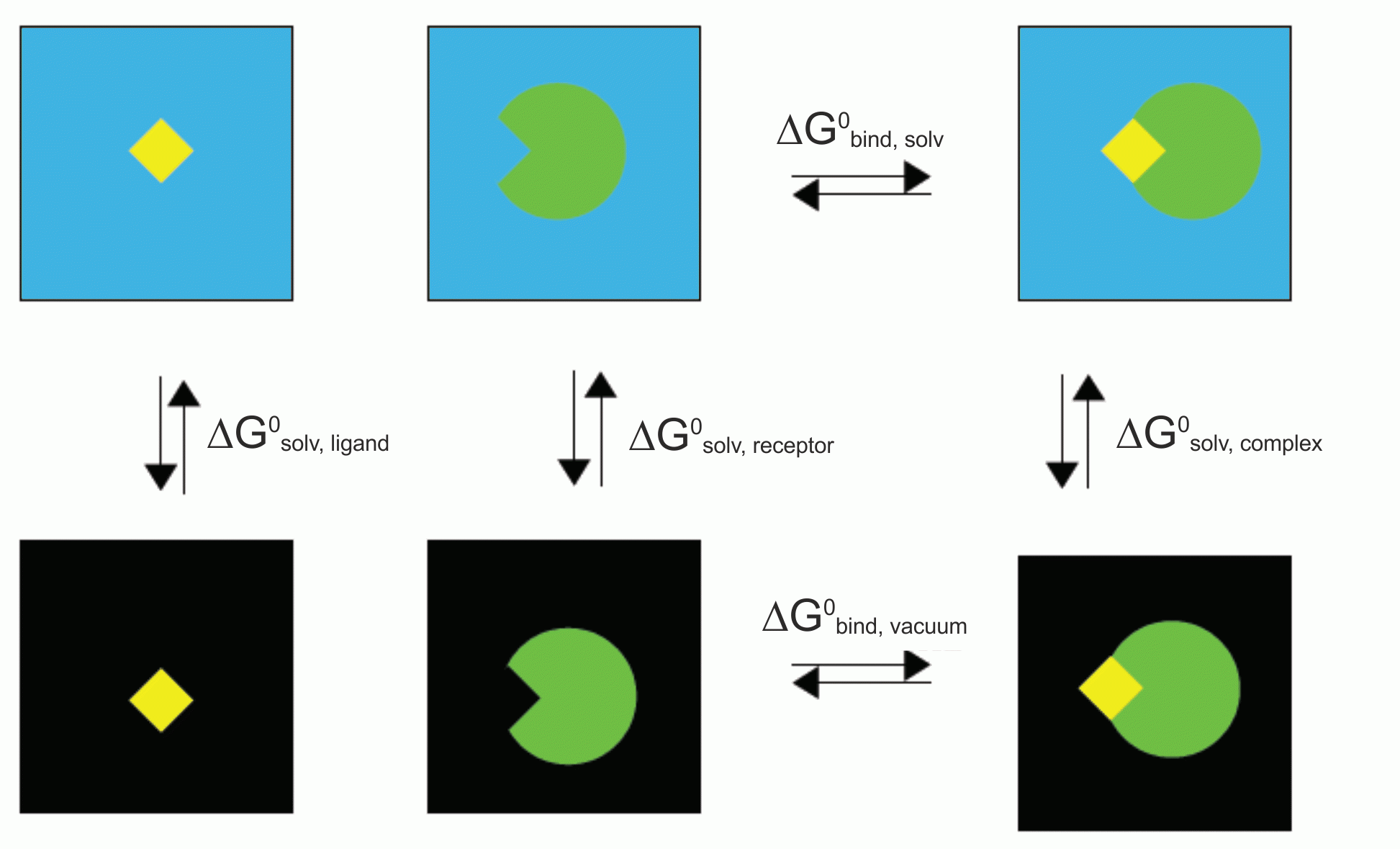
结合自由能定义为:

\[\D G_\text{bind} = G_\text{complex} - G_\text{free-protein} - G_\text{free-ligand}\]

根据定义, 在溶液中, 我们可将分子的自由能写为:

\[G = E_\text{gas}- TS_\text{gas} + G_\text{solvation}\]

其中的溶剂化自由能又可分解为极性部分和非极性部分:

\[G_\text{solvation} = G_\text{polar}+G_\text{nonpolar}\]

在MM-PBSA方法中, 气相的能量和熵的贡献根据MM方法计算:

\[\alg E_\text{gas} &= E_\text{MM}=E_\text{bond} + E_\text{angle} + E_\text{dihedral} + E_\text{vdw} + E_\text{coulomb} \\ S_\text{gas} &=S_\text{MM} \ealg\]

其中 \(E_\text{bond}\), \(E_\text{angle}\), \(E_\text{dihedral}\) 分别对应于键, 键角, 二面角的相互作用, \(E_\text{vdw}\) 和 \(E_\text{coulomb}\) 分别代表范德华和库仑静电相互作用.

MM-PBSA方法中的溶剂化能包含两部分, 极性溶剂化能和非极性溶剂化能. 极性溶剂化能来自于溶质和溶剂分子之间的静电相互作用, 计算时采用隐式的溶剂模型, 将溶剂视为连续的介质, 对相应的泊松玻尔兹曼方程进行线性化, 并数值求解.

\[G_\text{polar}=G_\text{PB}\]

非极性溶剂化自由能可根据经验的表面积方法进行计算, 因此也被称为表面溶剂化能. 计算时需要知道分子的溶剂可及表面积 \(A\) 与两个经验参数 \(\g\) 和 \(b\) :

\[G_\text{nonpolar} = G_\text{surface} = \g A + b\]

将上面的这些项结合起来, 就得到了MM-PBSA的自由能公式:

\[G = E_\text{MM}- TS_\text{MM} + G_\text{PB} + G_\text{surface}\]

实际计算时, 总的MM能量可利用GROMACS的工具进行计算. 计算时使用与模拟相同的的力场, 但注意当计算非键相互作用时不能使用截断. 数值求解PB方程一般使用APBS程序. 计算时, 需要指定立方格点的间距(可取0.5 Å), 还需要使用GROMOS的半径和电荷创建PQR文件. 纯水的介电常数使用 \(\e=78.45\), 溶质的介电常数一般取 \(\e=2\). 计算非极性溶剂化能的经验常数可使用 \(\g=0.0072\;\text{kcal/mol}\ \AA^2\), \(b=0\). 在APBS程序中表面积 \(A\) 由Shrake-Rupley数值方法计算的.

计算熵贡献时. 需要首先进行能量最小化(对非键相互作用不使用截断), 然后进行简正分析, 计算质量加权的Hessian矩阵, 并进行对角化, 利用得到的频率计算熵贡献:

\[S_\text{vib}=\Sum_i -R \ln(1-e^{-\b h\n_i})+{N_A \n_i e^{-\b h\n_i} \over T(1-e^{-\b h\n_i})}\]

其中 \(h\) 为普朗克常数, \(\n_i\) 为第 \(i\) 个频率, \(\b=1/k_BT\).

计算结合自由能时, 对蛋白质和配体复合物的平衡轨迹进行采样, 并分别计算复合物, 蛋白质, 配体的自由能, 根据 \[\D G_\text{bind} = G_\text{complex} - G_\text{free-protein} - G_\text{free-ligand}\] 即可得到结合自由能.

计算工具

对GROMACS用户而言, 长期以来没有一个方便的工具用于计算MM-PBSA自由能. 鉴于AMBER中有一个计算MM-PBSA的脚本mmpbsa.py, 所以以前的GROMACS用户往往先将得到的轨迹转换为AMBER格式, 然后在利用AMBER的工具进行自由能计算. 随着GROAMCS用户的逐渐增多, 目前, 已经有两个工具可以直接使用GROMACS的工具进行MM-PBSA自由能计算了.

1. GMXPBSAtool

这是基于bash/perl的脚本, 计算时调用已经安装的GROAMCS工具和APBS程序计算MM-PBSA. 脚本所起的作用主要是为GROAMCS工具和APBS程序准备输入文件, 并处理输出文件, 实际计算是由GROAMCS工具和APBS程序完成的. 因为是脚本程序, 不需要编译, 所以GMXPBSAtool使用比较方便, 可以很方便地进行大量计算. 程序修改也很方便, 只要清楚了各个程序的输入输出格式, 就可以用于不同版本的GROMACS和APBS.

程序包含三个脚本

  1. gmxpbsa0.sh: 初步计算. 只要为后面的计算进行设置, 包括: 检查输入文件, 从MD轨迹中抽取所需的帧, 使用APBS计算库仑作用的贡献. 如果在输入文件中定义了Alanine扫描, 也会对定义的残基进行Alanine突变.
  2. gmxpbsa1.sh: 计算极性和非极性的溶剂化能. 计算中最耗时的一步, 计算时可以并行.
  3. gmxpbsa2.sh: 统计所有帧的各项计算结果, 计算最终的结合自由能, 输出计算结果报告.

使用方法

遵照程序自带的文档HOW_TO_INSTALL, 解压后, 设置一下路径, 并保证当前使用的shell为bash, 即可使用. 当然前提是安装好GROMACS和APBS(安装方法在下面统一介绍).

运行时, 先在输入控制文件INPUT.dat中设置好GROMACS和APBS的路径, 再依次运行上面三个脚本即可.

运行结束后, Compare_MMPBSA.dat文件中列出了Alanine突变的计算结果, 相应的SUMMARY_FILES目录下保存了主要的结果.

2. g_MMPBSA

类似于GROMACS自带的工具, 使用方式也类似, GROAMCS用户可以很容易上手.

g_mmpbsa计算的结合自由能由以下部分组成:

计算时, 先使用g_mmpbsa分别计算每一部分, 所有计算完成后, 再按顺序运行程序附带的3个脚本进行后处理: MmPbSaStat.py计算平均结合能及其标准偏差/误差, MmPbSaDecomp.py进行能量分解, energy2fbc将能量转换为温度因子. 具体流程如下:

  1. 计算MM部分:

    g_mmpbsa -f traj.xtc -s topol.tpr -n index.ndx -mme -pdie 2 -decomp

    -mme指明计算范德华和库仑静电能

  2. 计算PB部分:

    g_mmpbsa -f traj.xtc -s topol.tpr -n index.ndx -i polar.mdp -nomme -pbsa -decomp

    使用-pbsa, 因为默认-nopbsa, 所以还需要使用-i提供溶剂化能参数输入文件
    使用-nomme是上一步已经计算了MM部分

  3. 计算SA部分:

    使用SASA模型: g_mmpbsa -f traj.xtc -s topol.tpr -n input.ndx -i apolar_sasa.mdp -nomme -pbsa -decomp -apol sasa.xvg -apcon sasa_contrib.dat

    使用SAV模型: g_mmpbsa -f traj.xtc -s topol.tpr -n input.ndx -i apolar_sav.mdp -nomme -pbsa -decomp -apol sav.xvg -apcon sav_contrib.dat

  4. 计算平均结合能:

    使用bootstrap方法: python MmPbSaStat.py -bs -nbs 2000 -m energy_MM.xvg -p polar.xvg -a apolar.xvg (or sasa.xvg)

  5. 能量分解:

    python MmPbSaDecomp.py -m contrib_MM.dat -p contrib_pol.dat -a contrib_apol.dat -bs -nbs 2000 -ct 999 -o final-contrib-energy.dat -om energymapin.dat

    必须按顺序写-m, -p, -a. 也可使用metafile.dat文件, 其中的内容为3个文件的路径(必须按照MM, polar, apolar的顺序). 我们所需要的能量均写在这里. final-contrib-energy.dat文件中为能量分解的具体内容, 另外一个输出文件energymapin.dat是为下一命令准备的.

  6. 转换为温度因子

    python energy2fbc -s md.tpr -i energymapin.dat -n input.ndx -c complex.pdb -s1 s1.pdb -s2 s2.pdb

    -s1, -s2为分链显示, s1和s2链的原子数相加必须与之前计算中体系的总原子数相等. 脚本会将残基按温度因子(b-factor)进行着色, 在PyMol中选择按b-factor着色即可看到效果.

编译

作者的网站上给出了二进制版本的g_mmpbsa程序, 如果你的机器够新, 一般可以直接使用. 使用前需要先安装GROMACS和APBS. 如果你使用Ubuntu系统, 安装GROMACS和APBS很方便

sudo apt-get install gromacs
sudo apt-get install apbs

然后将gmx_pbsa程序复制到选定的目录下(建议放于GROAMCS主目录下的bin中, 和其他GROAMCS工具放一起), 添加可执行属性: chmod u+x ./g_mmpbsa即可使用了.

由于作者编译gmx_pbsa时使用了Intel编译器的一些优化选项(如AVX, SSE之类), 致使在一些比较老的机器上使用程序时, 会出现FATAL: kernel too old. Segmentation fault或Illegal instruction (core dumped)之类的错误. 在这种情况下, 就只能在你自己的机器上重新编译了. 在编译g_mmpbsa前, 需要下面的一些库:

这些文件在GROMACS和APBS编译之后得到的. 如果你没有权限使用上面的命令安装GROMACS和APBS, 那你还需要自己编译GROMACS和APBS. 编译时, 最好对这三个程序使用相同的编译器, 否则出现错误的话, 不易解决.

  1. 编译GROMACS 4.6.5(新版本已经支持GMX 5.x)

    g_mmpbsa支持GROMACS–4.6.x, 尚未支持5.x. 编译时, GROMACS需要生成静态库, 因为g_mmpbsa不支持MPI, 不能并行, 因此编译GROMACS时, 必须明确地禁用MPI和GPU选项. 此外, 还需要注意fftw的单双精度问题, 需要安装双精度版本的fftw.

    tar -zxvf gromacs-4.6.5.tar.gz
cd gromacs-4.6.5
mkdir build
cd build
cmake ../ -DCMAKE_INSTALL_PREFIX=/opt/gromacs -DGMX_PREFER_STATIC_LIBS=ON -DGMX_GPU=off
make
make install

  2. 编译APBS 1.3

    g_mmpbsa目前也支持APBS–1.4, 编译方法请参考程序网站上的说明.

    编译时, 如果环境变量含有ifort, 会自动选择intel的ifort进行编译, 这样g_mmpbsa也应当使用ifort来编译.

    tar zxvf apbs-1.3-source.tar.gz
cd apbs-1.3-source/
./configure --prefix=/path/to/apbs-1.3
make
make install

  3. 编译fftw单双精度版

    cd fftw-3.1.2
./configure --enable-float --enable-mpi --prefix=/opt/fftw-3.1.2
make
make install
make distclean
./configure --disable-float --enable-mpi --prefix=/opt/fftw-3.1.2

  4. 编译g_mmpbsa

    tar zxvf RashmiKumari-g_mmpbsa-v1.1.0-7-gcf6c583.tar.gz
cd RashmiKumari-g_mmpbsa-cf6c583/
mkdir build
cd build
cmake -DGMX_PATH=/opt/gromacs \
-DAPBS_INSTALL=/opt/apbs \
-DAPBS_SRC=/path/to/apbs-1.3-source \
-DCMAKE_INSTALL_PREFIX=/opt/g_mmpbsa \
-DFFTW_LIB=/opt/fftw-3.3.4/lib ..
make
make install

  5. 完善Python环境

    g_mmpbsa附带的tools文件夹中包含了几个用于后处理的Python脚本. 如果直接执行脚本时出错, 那你需要对Python环境进行完善, 安装缺少的模块. 由于Pyhton版本众多, 注意要下载与已安装的Python版本匹配的模块. 网站Unofficial Windows Binaries for Python Extension Packages上提高各种版本的模块供下载, 需要的话可以下载.

几点说明

  1. 这两个工具都可以用于计算MMPBSA的结合能, 根据袁曙光的个人经验, 使用默认参数时, 在精度上GMXPBSA似乎优于g_mmpbsa而且使用也更方便.

  2. APBS程序可使用OpenMP进行并行, 通过环境变量控制使用的核/处理器数目, export OMP_NUM_THREADS=X

  3. APBS程序求解PB方程的速度有限, 因此体系大时, 计算很耗时. 卢本卓提出了一种求解PB方程的改进方法, 且发布了求解程序AFMPB. 如果使用AFMPB替代APBS, 应该可以提高计算速度.

  4. 在轨迹不平衡的情况下, 计算PB部分时可能会变得非常慢, 所以需要挑选足够平衡的轨迹进行计算

  5. 默认计算能量时, 每帧都会计算, 这样可能会特别费时. 在这种情况下你可以使用trjconv抽取一步分轨迹进行计算, 以减少运算量

    trjconv -f md.xtc -o trj_8-10ns -b 8000 -e 10000 -dt 100

  6. 在具体的应用中, 尤其是在多条蛋白质MD中, 会需要选择不同的链作为单体, 这时候可使用make_ndx命令将两条蛋白链分别设为不同的组.

  7. 对结合能进行能量分解可得到不同残基对总结合自由能的贡献, 用以考察每个残基对自由能的贡献大小. 这方面的一个应用可参考MM-PBSA Captures Key Role of Intercalating Water Molecules at a Protein-Protein Interface. 论文中所考察的蛋白质, 在某些氨基酸发生突变后, 与配体的结合能力会增加1000倍, 这主要是表面的水分子在起作用. 作者利用MM-PBSA方法计算了结合自由能, 发现天然的与突变后的结合自由能有明显的差异, 可以有效地区分结合的强弱.

参考资料

评论

◆本文地址: , 转载请注明◆
◆评论问题: https://jerkwin.herokuapp.com/category/3/博客, 欢迎留言◆
前一篇:　
后一篇:　
访问人次(2015年7月 9日起): | 最后更新: 2024-11-01 02:53:58 UTC | 版权所有 © 2008 - 2024 Jerkwin 个