空间分布函数SDF的计算及三维图示

2014-05-13 17:52:00 硕士生李耀对此文有贡献

基本概念

分子动力学模拟中常以径向分布函数(radical distribution function, RDF)来描述粒子周围环境的分布特性, 并表征其短程有序性. 分布函数的概念可推广到三维, 三维空间的分布函数被称为空间分布函数(spatial distribution function, SDF), 可定义为与粒子的局部数密度与平均数密度之比 $\Omega(x,y,z)={\rho(x,y,z) \over \bar \rho}$, 数学实质是三维的某种密度分布.

一般来讲, 三维密度函数的图示方法有好几种, 其中主要的几种在量子化学的轨道图示中都有使用过, 如点云图, 径向分布图, 角度分布图, 等值面图, 切面图. 此外还有几种图示方法是计算流体力学中常用的, 在化学中使用较少.

计算方法

SDF计算过程与具体体系相关, 不易统一, Gromacs提供了一个g_spatial的工具, 但使用不是很方便. 很多人使用gOpenMol, 如 Distrubutions of Counterions around DNA. Molecular Dynamics Simulations Results. 我没有使用过gOpenMol, 无法评论.

下面是SDF的计算方法

1. 中心分子: 确定要分析的目标分子
2. PBC平移: 将每一个目标分子平移至原点作为中心, 根据周期性边界条件(periodic boundary condition, PBC)对其他分子进行相应平移
3. 最佳叠合/旋转一致: 对PBC平移后的构型进行最佳叠合或旋转, 使中心分子取向一致
4. 统计密度: 利用中心分子取向一致后的构型统计其周围粒子的密度分布

几点说明

• PBC平移的方法可参考我的博文取整截断函数及其在PBC中的使用.

• 若每帧轨迹中含有N个目标分子, 则每帧轨迹最多可得到N个构型. 使用每个目标分子作为中心分子是为了充分利用每帧的数据, 如果你的轨迹文件时间很长, 每帧只使用一个中心分子也可以

• 最佳叠合/旋转一致过程我以前也简略说过. 如果中心分子在MD过程中构型变化不大, 或其关键部分是刚性的, 变化不大, 那么只要选择中心分子上不共线的三个原子, 第一个原子作原点, 第二个原子处于x轴正向, 第三个原子处于xy平面, z轴垂直于三个原子所在的平面, 将所有PBC平移后的构型都旋转至标准取向即可. 严格来说, 应该对中心分子做最佳叠合, 使所有中心分子相对于参考中心分子的位置的偏差(RMSD)最小. 这不是一个简单的工作, 但可利用四元数方法解决.

• 多个分子的叠合显示可利用Jmol或VMD. VMD支持的多帧XYZ文件, 原子类型及数目必须固定, 有时使用不便; Jmol支持的XYZ文件更宽泛, 但无法操控太大的文件.

• VMD处理大文件的能力很赞, 一百万个原子轻松, 再多点稍困难. 我最大操作四百万个原子, 比较卡了.

• 统计密度时, 一般是使用直角坐标, 将整个空间分为若干均匀的小格子, 然后统计每个小格子中出现的原子个数, 再除以小格子的体积, 平均, 得到原子的数密度, 将此密度与平均密度相比, 得到SDF.

• 统计密度时, 可只统计中心分子附近某一区域内的(可由RDF获知), 因离中心分子很远的地方SDF基本趋于均匀, 意义不大

• 一般需要对多帧轨迹进行计算统计, 直至算出的SDF数值收敛.

• 一般将SDF保存为cube文件. cube文件格式始于Gaussian, 但现在已基本成为标准格式了. 具体格式可参考Gaussian手册或卢天的博文 Gaussian型cube文件简介及读、写方法和简单应用.

• cube文件的可视化程序很多, 大凡好点的分子可视化程序都支持, 常用的如GaussView, VMD, Jmol, ChemCraft, Chemirea, gOpenmol. 如果要同时显示多个等值面, GaussView可能不是一个好的选择, VMD可能最简单, 具体方法可参考 VMD 画cube文件等密度面图（轨道或电子密度等）

代码

• CntAtm
• RotMol
• SDF

具体示例

以一帧含5000个水分子的构型为例, 计算水分子周围O原子的SDF.

1. 目标分子, 水分子, 此帧5000个
   

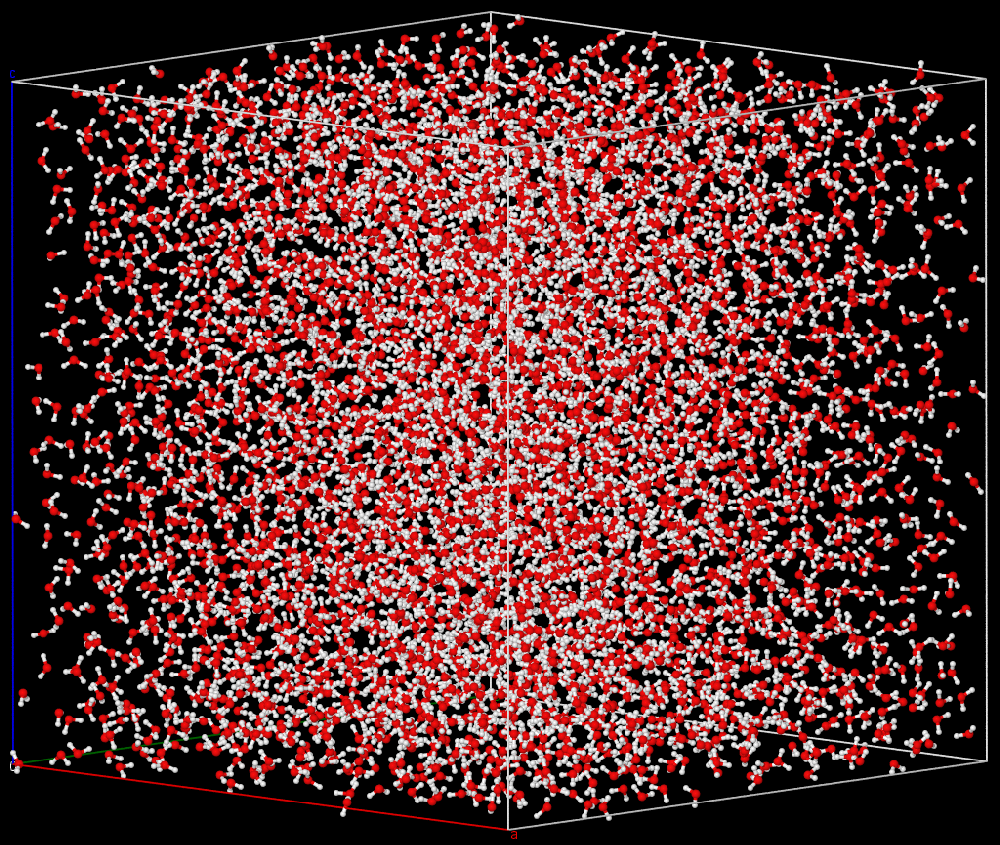
2. 以每个水分子为中心, 其余水分子PBC平移至[-L/2, L/2]范围内, 共得5000个构型. 其中一个如下
   

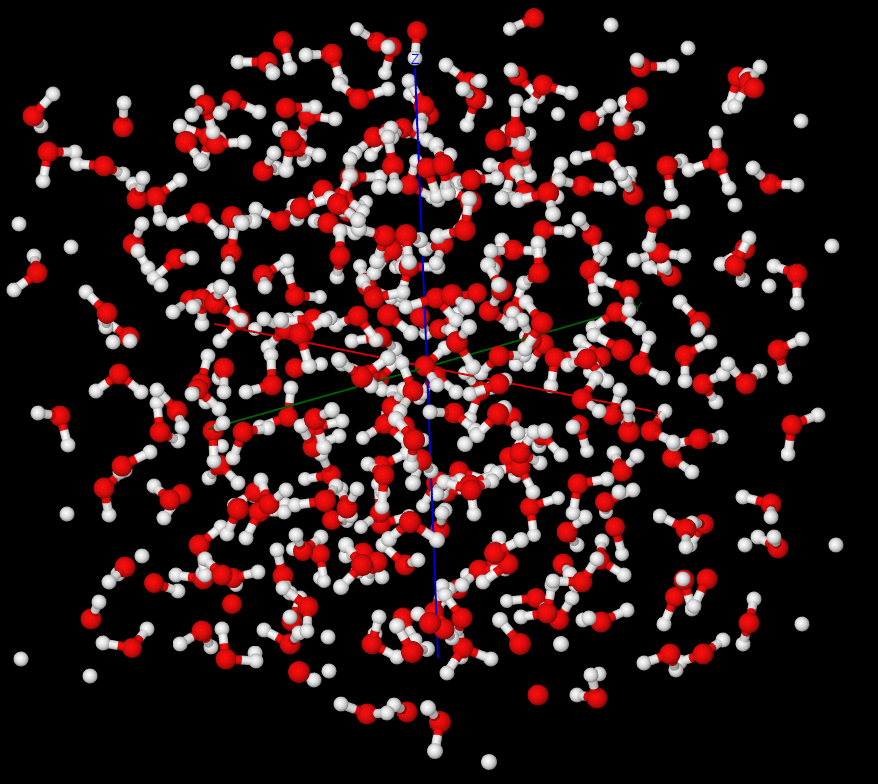
3. 将中心水分子进行叠加显示, 可见最佳叠合/旋转一致前, 由于取向随机, 中心O原子周围H原子基本成球状分布,
   
   中心水分子周围其他水分子分布也呈均匀分布
   

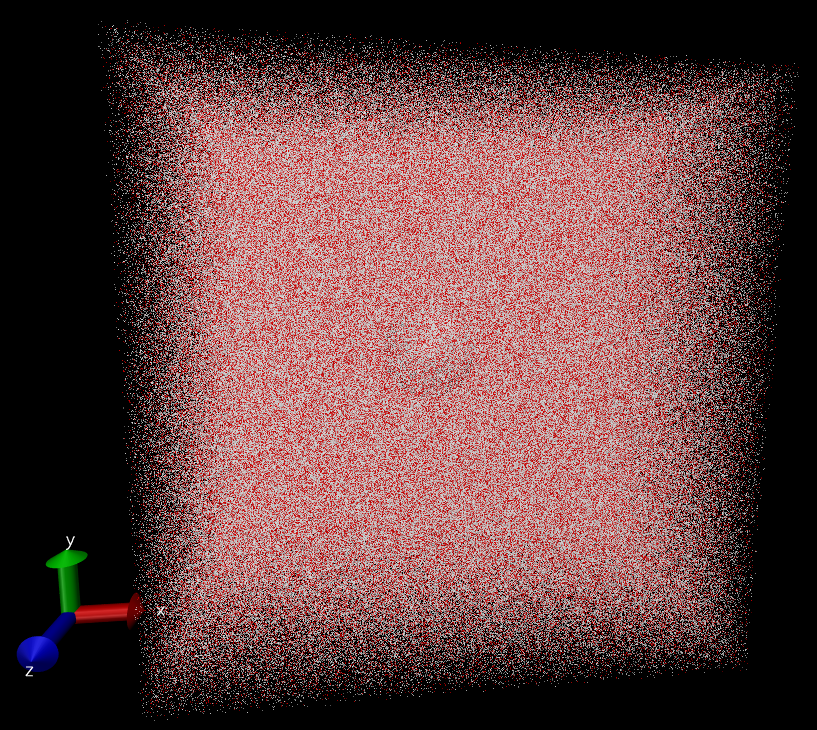
4. 将中心水分子旋转一致后, 中心O原子周围H原子分布与单个水分子类似, 但由于水分子构型在MD过程中有变化, 不会完全重合
   

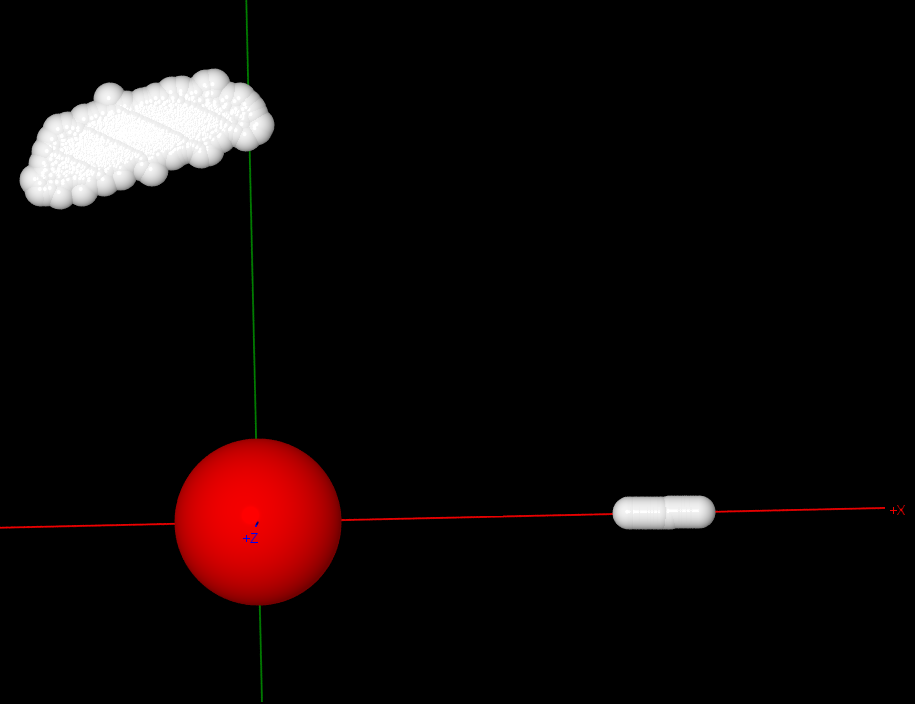
5. 旋转一致后, 中心水分子周围其他水分子的分布不再均匀, 显示出各向异性, 这种各向异性从叠合后的构型图也可看出,
   O原子分布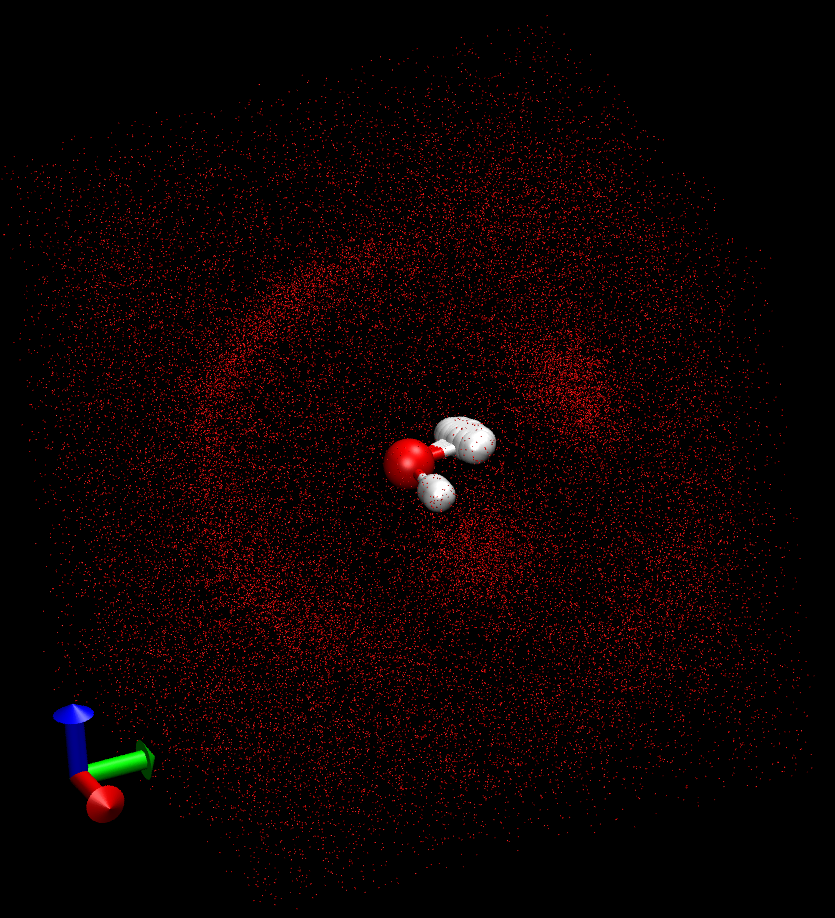
   H原子分布
   水分子分布

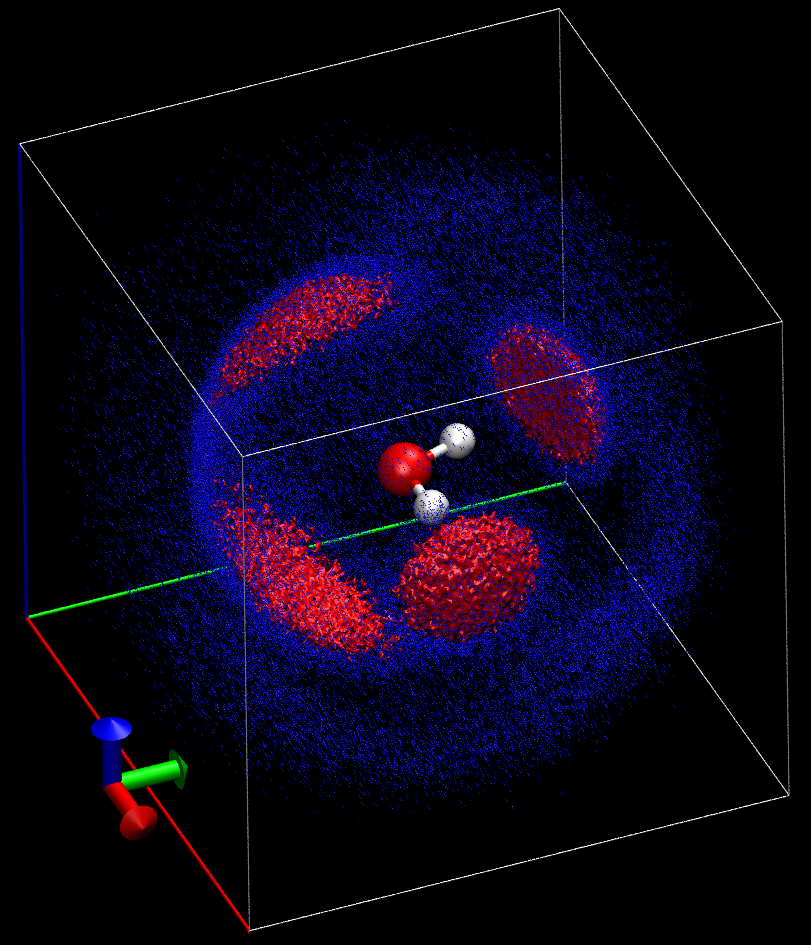
6. 计算cube文件, 利用VMD显示等值面, 两个不同值的等值面(蓝色为5, 红色为10)如下, 水分子周围H氢键的四面体结构很明显