2014-11-20 10:16:44
在数据可视化时, 人们常常使用颜色映射图, 就是将一定范围内的数据跟一定范围内的颜色对应起来, 不同的颜色表示数据的不同大小. 这样的图在展示的时候很直观, 很清晰, 也很吸引眼球, 所以在科技论文中常常可以看到.
很多人在做颜色映射图时, 没有特别留意选用什么样的颜色范围, 颜色和数据之间以什么方式对应. 大多数人直接使用了彩虹映射图(从红到蓝的线性映射, 类似可见光颜色, 很多软件的默认设置).
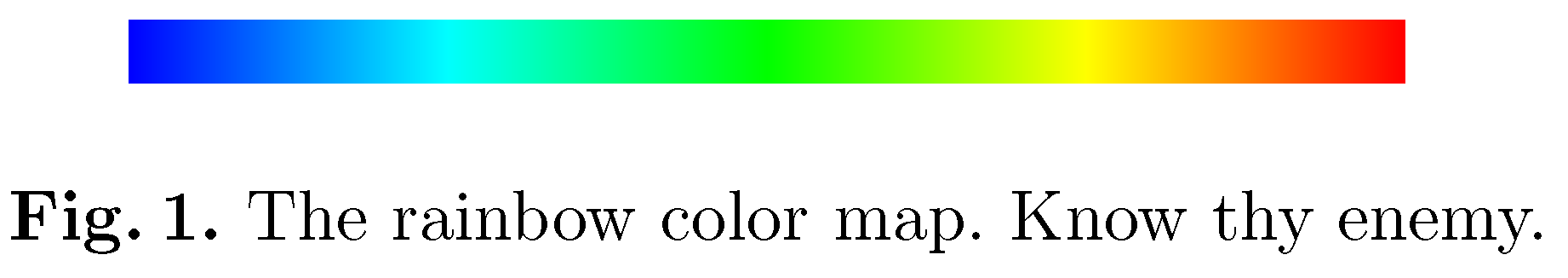
这种图看起来颜色多样, 给人很漂亮的感觉. 可细究起来, 这种彩虹映射图是非常差的一种颜色映射方案, 以致于有人专门写文章指出, Rainbow Color Map (Still) Considered Harmful. 简单说来, 彩虹映射方案的主要缺陷在于颜色不均匀, 不同颜色之间过渡不平滑, 在显示数据时很容易将一些细节淹没. 更详细的讨论可参看这篇文章, Why Should Engineers and Scientists Be Worried About Color?.
既然彩虹映射方案很差, 那什么样的颜色映射方案好呢? Brewer的文章就讨论了这个问题, 并专门提供了一些好的方案供你在线选择. 在作图时, 最好使用这些好的颜色映射方案. 虽然它们看起来可能没有彩虹映射方案那么炫, 但对于正确反映数据的特征很有帮助, 而这正是科学数据可视化中最重要的一点.
有人还提出了一种被称为分散颜色映射的方案, 并证实效果不错. 这个方案的论文, 数据, 代码可以在这里找到: Diverging Color Maps for Scientific Visualization. 具体的效果也请参考论文中的对比图.
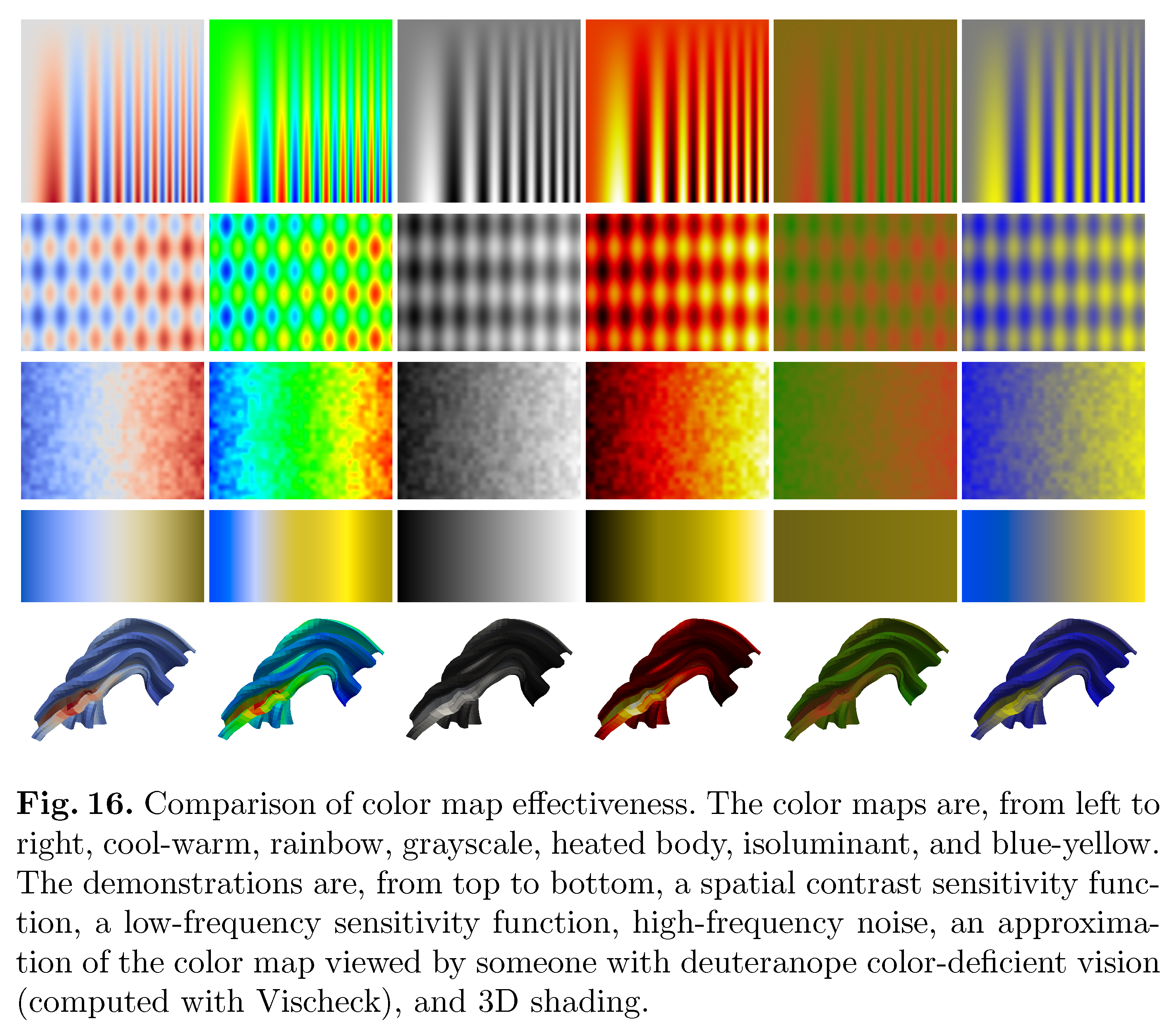
分散颜色映射方案的精确计算很复杂, 这样在使用时很不方便. 一个简单的解决方式就是将其颜色的RGB值拟合成简单的解析表达式.
根据上面网址给出的257个数据点(文件CoolWarmFloat257.csv), 我发现对红色R和蓝色B可以很好的利用高斯函数进行拟合,
对于绿色G, 我没有找到合适的单一解析表达式, 而只能以 $x=0.5$ 为分割点, 进行分段拟合, 前半段采用高斯函数, 后半段采用二次函数, 效果也还不错.
拟合采用的函数形式如下
\[\begin{align} \text{Gauss}(y_0, A, x_0, w, x) &= y_0+A \exp\left(-{(x-x_0)^2 \over 2w^2}\right) \\ \text{Circle}(y_0, a, b, x_0, x) &=y_0+b\sqrt{1-{(x-x_0)^2 \over a^2}} \end{align}\]下面是论文中给出的冷暖方案及其数据

x R G B RGB
0.0 59 76 192 #3B4CC0
0.03125 68 90 204 #445ACC
0.0625 77 104 215 #4D68D7
0.09375 87 117 225 #5775E1
0.125 98 130 234 #6282EA
0.15625 108 142 241 #6C8EF1
0.1875 119 154 247 #779AF7
0.21875 130 165 251 #82A5FB
0.25 141 176 254 #8DB0FE
0.28125 152 185 255 #98B9FF
0.3125 163 194 255 #A3C2FF
0.34375 174 201 253 #AEC9FD
0.375 184 208 249 #B8D0F9
0.40625 194 213 244 #C2D5F4
0.4375 204 217 238 #CCD9EE
0.46875 213 219 230 #D5DBE6
0.5 221 221 221 #DDDDDD
0.53125 229 216 209 #E5D8D1
0.5625 236 211 197 #ECD3C5
0.59375 241 204 185 #F1CCB9
0.625 245 196 173 #F5C4AD
0.65625 247 187 160 #F7BBA0
0.6875 247 177 148 #F7B194
0.71875 247 166 135 #F7A687
0.75 244 154 123 #F49A7B
0.78125 241 141 111 #F18D6F
0.8125 236 127 99 #EC7F63
0.84375 229 112 88 #E57058
0.875 222 96 77 #DE604D
0.90625 213 80 66 #D55042
0.9375 203 62 56 #CB3E38
0.96875 192 40 47 #C0282F
1.0 180 4 38 #B40426
拟合结果
\[\alg &R: 255 \times \text{Gauss}( 0.00973, 0.95734, 0.68447, 0.40538, x) \\ &G: \begin{cases} 255 \times \text{Gauss}( -0.70487, 1.57141, 0.51782, 0.54700, x)\; &x \in [0,0.5] \\ 255 \times \text{Circle}(-0.97384, 0.96412, 1.96264, 0.17749, x)\; &x \in (0.5,1.0] \end{cases}\\ &B: 255 \times \text{Gauss}( -0.05837, 1.05992, 0.28797, 0.39754, x) \ealg\]拟合效果图
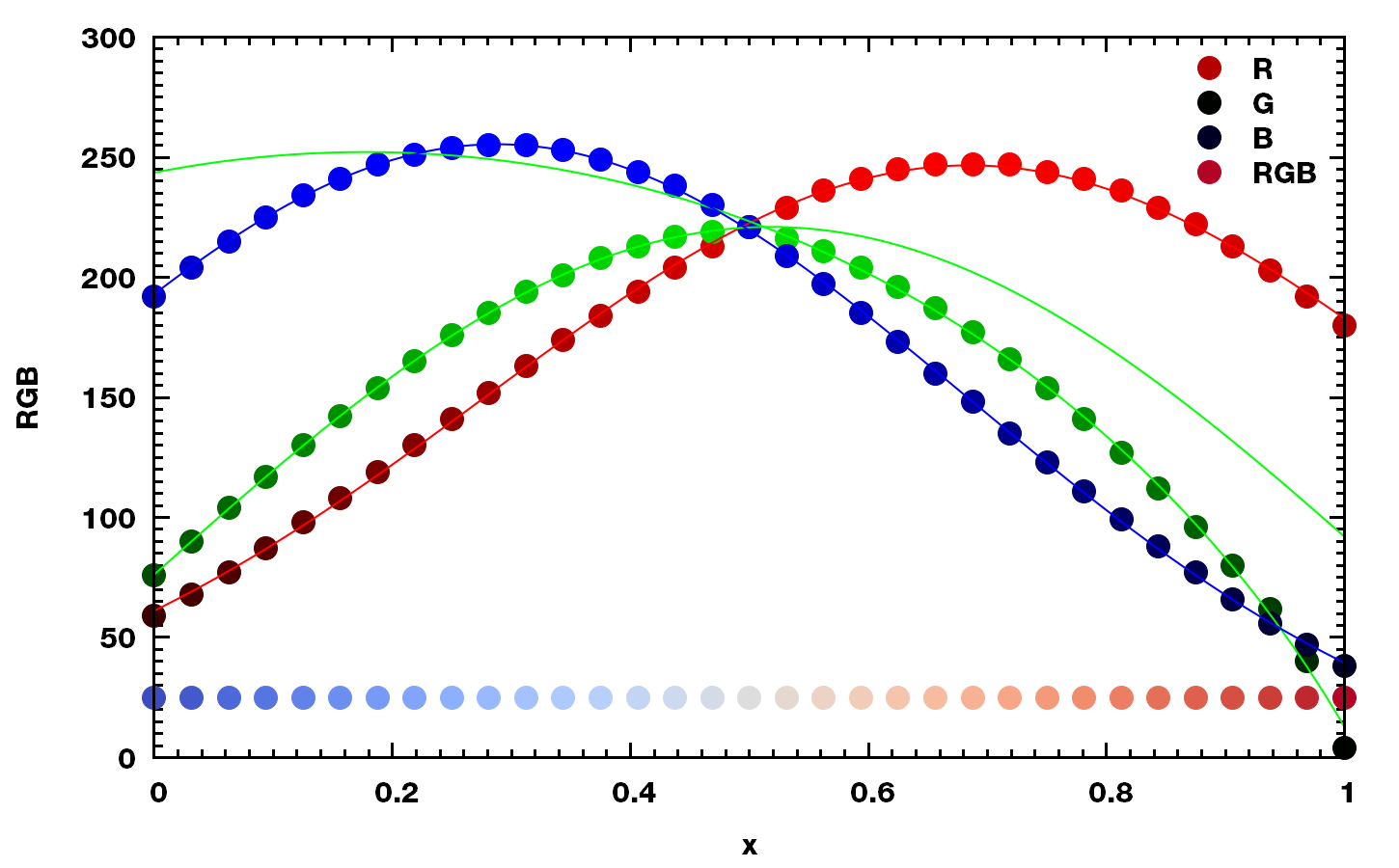
可见拟合效果相当不错, 展示数据时人眼觉察不到解析式效果与精确值效果之间的差异.
这种拟合解析式的方法可以同样运用到论文中给出的其他颜色方案.

更普遍的, 或许能直接给出任意方案的近似解析式. 我没有那么多时间, 有兴趣的人可以试着推广一下. 若得到了肯定的答案, 还烦请告知我.
