使用GROMACS计算粘度|Jerkwin

2018-03-08 21:10:52 整理: 高庆林; 补充: 李继存

0. 基础知识

维基百科 Viscosity
GROMACS手册粘度计算
参考文献
- Berk Hess; Determining The Shear Viscosity Of Model Liquids From Molecular Dynamics Simulations; J. Chem. Phys. 116(1): 209, 2002; 10.1063/1.1421362
- Lifeng Zhao, Tao Cheng, Huai Sun; On The Accuracy Of Predicting Shear Viscosity Of Molecular Liquids Using The Periodic Perturbation Method; J. Chem. Phys. 129(14): 144501, 2008; 10.1063/1.2936986
- Yanmei Song, Lenore L. Dai; The Shear Viscosities Of Common Water Models By Non-equilibrium Molecular Dynamics Simulations; Molecular Simulation 36(7-8): 560-567, 2010; 10.1080/08927021003720553
- A. P. Markesteijn, Remco Hartkamp, S. Luding, J. Westerweel; J. Chem. Phys. 136(13): 134104, 2012; 10.1063/1.3697977
- 王玲, 程涛, 李丰, 戴建兴, 孙淮; 新型胍盐离子液体剪切粘度性质的预测; 化学学报, 68(17): 1673-1680;

关键问题:

不同类型流体的粘度有什么区别?
哪种类型流体的粘度GROMACS可以计算?
使用的方法有什么限制?

以下为使用GROMACS的周期性微扰方法(PPM)计算水的粘度的简单流程, 供参考.

1. 创建水盒子, 构建拓扑文件并进行能量最小化

为计算粘度, 水盒子z方向的长度最好要取x/y方向长度的三倍以上, 因为z方向长度越大, 越容易收敛. 如果要做出x方向速度 $v_x$ 随z大小变化的完整剖面, z方向长度的最好超过 $2\p$.

这里我们选用 $4\times4\times12\ \text{nm}^3$ 的盒子, 填充4500个SPC/E模型的水分子. 可以使用packmol或GROMACS自带命令solvate填充盒子.

得到水盒子之后, 我们要创建拓扑文件. 使用的拓扑文件如下, 其中的参数来自于OPLS-AA力场. 我们没有在拓扑文件中使用#include语句, 而是直接添加了需要的内容(原子类型等), 这并非必要, 只不过更容易理解拓扑文件的结构.

对水盒子进行能量最小化, 消除不合理的接触. 对于水盒子这样简单的体系来说, 不进行能量最小化也完全没有问题. 但如果模拟其他的分子, 最好还是先进行一下能量最小化, 避免后面预平衡的时候发生崩散的情况.

2. NVT预平衡

对简单的水盒子来水, 这一步骤并非必要, 但模拟其他分子时, 最好不要忽略这一步骤.

使用tcoupl = v-rescale进行NVT预平衡.

3. NPT预平衡

对水盒子进行NPT预平衡, 使其密度达到合理值.

首先使用tcoupl = v-rescale, pcoupl = berendsen进行初步的快速平衡.

待温度和压力达到设定值后, 换用tcoupl = nose-hoover, pcoupl = Parrinello-Rahman进行更长时间的精确平衡.

盒子越大, 分子越复杂, 所需预平衡时间越长. 我们进行1 ns的NPT预平衡.

4. NVT预平衡

使用NPT预平衡所得的最后一步构型作为初始构型进行NVT预平衡. 选择初始构型的更好方法是使用NPT预平衡中瞬时盒子大小最接近平均大小, 或瞬时压力最接近设定压力的那帧.

使用tcoupl = nose-hoover, pcoupl = no进行NVT预平衡.

预平衡所需的模拟时间要根据体系而定. 对简单的分子, 纳秒级别足够了.

5. NVT非平衡(粘度)模拟

使用NVT预平衡所得的最后一步构型进行非平衡模拟以计算粘度.

模拟时仍使用NVT系综, tcoupl = nose-hoover.

尽量提高能量与trr轨迹的输出频率, 如nstxout = 10, nstvout = 10, nstxout-compressed = 1, nstenergy = 1, nstcalcenergy = 1. 这是因为计算粘度和速度剖面时所用的帧数越多越好.

打开非平衡模拟选项cos_acceleration = 0.025. 这里设置的加速度振幅数值不能太大, 也不能太小, 具体什么值合适有时需要测试. 原因参考前面提到的文献.

不同的模拟条件会产生相应的误差. 目前使用PPM方法计算水的粘度会有不同程度的低估, 尤其是在低温条件下, 具体情况需要看相关的文献. 理论上较大的模拟体系, 较小的加速度振幅下测得的粘度会更加接近实验值, 但这需要长时间的抽样并进行多次模拟取平均.

具体需要进行多长时间的模拟, 需要根据实际情况确定. 模拟体系越大, 需要的模拟时间越长. 为了能在相同条件下增加抽样数, 减少计算误差, 模拟时间越长越好.

6. 计算粘度和速度剖面

通过自己编程来计算粘度存在一定的难度, 所以我们尽量使用GROMACS已有的命令来达到目的.

可以使用gmx energy抽取粘度的倒数, 然后换算成粘度. 但这种方法有时波动很大, 所以必须保证所得结果收敛.

Energy         Average   Err.Est.       RMSD  Tot-Drift
-------------------------------------------------------------------------------
1/Viscosity    1456.95        3.5    121.793    11.4993  (m s/kg)

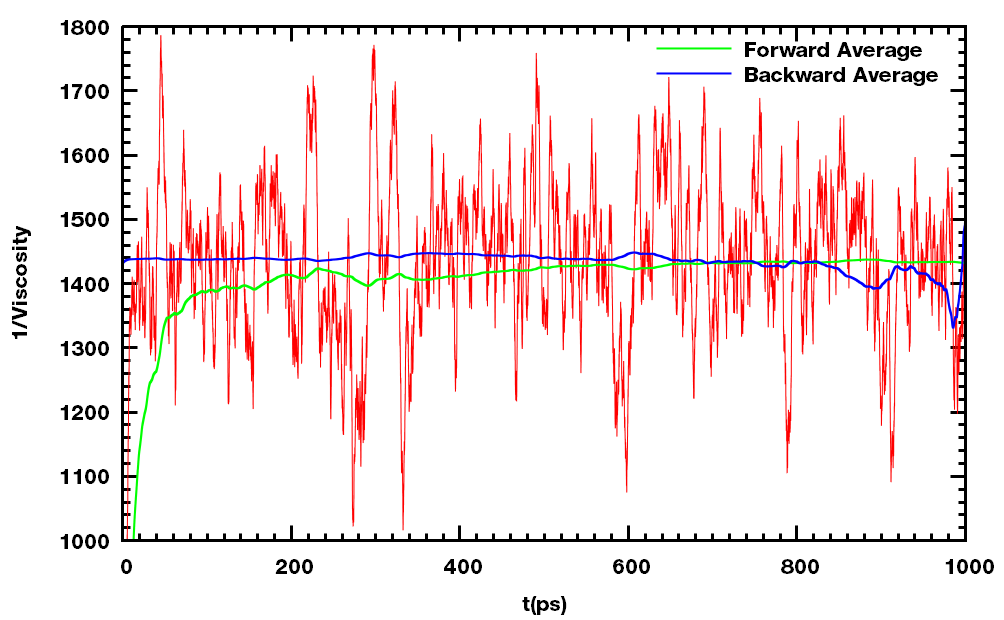
通过这种方法计算25℃下水的粘度, 结果为0.6836 mPa·s, 实验值为0.894 mPa·s. 目前文献报道的最好结果是0.72 mPa·s. 所以, 可能需要适当的调节参数以及采用不同的模型来得到更好的结果.

也可以计算z-vx速度剖面, 然后拟合得到粘度. 需要注意的是, 至少需要相同数量级的模拟时间来建立合理的速度分布.

统计速度剖面时, 既可以使用分子的质心速度, 也可以使用质量平均速度. 对小分子这二者区别不大, 对长链分子, 质量平均速度可能更好, 但需要测试才能知道.

计算速度剖面的脚本如下.

zvx.bsh
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41	awk ' BEGIN { # 定义原子质量 Mas["C"]=12.01; Mas["H"]=1.008; Mas["O"]=16.00; Mas["N"]=14.01; Mas["P"]=30.97 Ntot=1000 # 定义要计算的帧数 YesCOM=1 # 统计质心速度还是原子速度 Zmin=0; Zmax=10.6; dZ=0.2 # 定义计算区间, 分格间距 Nfrm=0; N=int((Zmax-Zmin)/dZ) for(i=0; i<=N; i++) { Z[i]=Zmin+idZ; Vx[i]=0; Mtot[i]=0; Nwat[i]=0 } } # 此行只含一列, 且此列皆为数字, 说明此行为原子数目行. /[0-9]+/为正则表达式 NF==1 && $1~/[0-9]+/{ Nfrm++ } !YesCOM && NF>6 { atm=substr($2,1,1); m=Mas[atm] # 提取第二列的第一个字母, 也即元素符号, 获取其质量 z=$(NF-3); i=int((z-Zmin)/dZ) Mtot[i] += m Vx[i] += m$(NF-2) # x方向速度 if(Nfrm>Ntot) exit } YesCOM && NF>6 && $2~/OW/ { # 根据 OW 原子统计质心速度 z = Mas["O"]$(NF-3); vx = Mas["O"]$(NF-2) # O 的z坐标, x方向速度 getline; z += Mas["H"]$(NF-3); vx += Mas["H"]$(NF-2) # H1的 getline; z += Mas["H"]$(NF-3); vx += Mas["H"]$(NF-2) # H2的 M=Mas["O"]+2*Mas["H"] z /= M; vx /= M # 质心坐标和速度 i=int((z-Zmin)/dZ) Nwat[i]++; Vx[i] += vx if(Nfrm>Ntot) exit } END { print "# Z: ["Zmin":"Zmax":"dZ"] Frames: " Nfrm if(YesCOM) { for(i=0; i<=N; i++) if(Nwat[i]>0) printf"%f %f\n", Z[i], Vx[i]/Nwat[i] } if(!YesCOM) { for(i=0; i<=N; i++) if(Mtot[i]>0) printf"%f %f\n", Z[i], Vx[i]/Mtot[i] } } ' traj.gro >zvx.xvg

zvx.bsh

awk ' BEGIN {
	# 定义原子质量
	Mas["C"]=12.01; Mas["H"]=1.008;
	Mas["O"]=16.00; Mas["N"]=14.01; Mas["P"]=30.97

	Ntot=1000                  # 定义要计算的帧数
	YesCOM=1                   # 统计质心速度还是原子速度
	Zmin=0; Zmax=10.6; dZ=0.2  # 定义计算区间, 分格间距
	Nfrm=0; N=int((Zmax-Zmin)/dZ)
	for(i=0; i<=N; i++) { Z[i]=Zmin+i*dZ; Vx[i]=0; Mtot[i]=0; Nwat[i]=0 }
}

# 此行只含一列, 且此列皆为数字, 说明此行为原子数目行. /[0-9]+/为正则表达式
NF==1 && $1~/[0-9]+/{ Nfrm++ }

!YesCOM && NF>6 {
		atm=substr($2,1,1); m=Mas[atm] # 提取第二列的第一个字母, 也即元素符号, 获取其质量
		z=$(NF-3); i=int((z-Zmin)/dZ)
		Mtot[i] += m
		Vx[i] += m*$(NF-2) # x方向速度
	if(Nfrm>Ntot) exit
}

YesCOM && NF>6 && $2~/OW/ {   # 根据 OW 原子统计质心速度
			 z  = Mas["O"]*$(NF-3); vx  = Mas["O"]*$(NF-2) # O 的z坐标, x方向速度
	getline; z += Mas["H"]*$(NF-3); vx += Mas["H"]*$(NF-2) # H1的
	getline; z += Mas["H"]*$(NF-3); vx += Mas["H"]*$(NF-2) # H2的

	M=Mas["O"]+2*Mas["H"]
	z /= M; vx /= M    # 质心坐标和速度
	i=int((z-Zmin)/dZ)
	Nwat[i]++; Vx[i] += vx
	if(Nfrm>Ntot) exit
}

END {
	print "# Z: ["Zmin":"Zmax":"dZ"]    Frames: " Nfrm
	if(YesCOM)  { for(i=0; i<=N; i++) if(Nwat[i]>0) printf"%f %f\n", Z[i], Vx[i]/Nwat[i] }
	if(!YesCOM) { for(i=0; i<=N; i++) if(Mtot[i]>0) printf"%f %f\n", Z[i], Vx[i]/Mtot[i] }
}
' traj.gro >zvx.xvg

需要注意的是, 使用这个脚本计算速度剖面时, 需要的构型文件traj.gro可能巨大, 脚本的处理速度也有点慢. 一种解决方法就是使用编译型语言直接读取trr文件, 具体方法参见GROMACS二进制文件的读取.

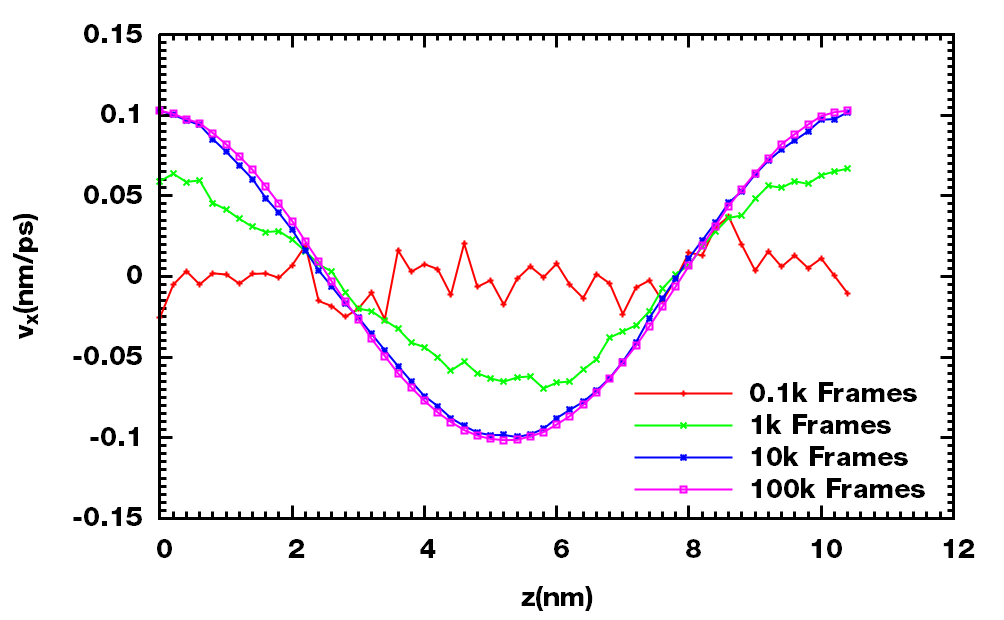
文献提到在模拟时间足够长的情况下, 会得到余弦形式的速度剖面, 所以可以使用速度剖面来判断选取的加速度振幅是否符合Hess的理论. 统计足够多的构型应该可以得到正常的余弦速度剖面. 下面是统计100, 1000, 10000, 100000帧时z-vx的速度剖面:

理论上, 速度剖面的形式如下

\[v_x(z)=V\cos \left({2\p z \over l_z} \right)\] \[V=A {\r \over \h} \left( {l_z \over 2\p} \right)^2\]

其中, $A$ 为加速度振幅, 对于NVT系综来说, 密度 $\r$ 和 $l_z$ 的大小是不变的. 通过拟合速度剖面可以得到 $V$. 这样就可以间接求出粘度

\[\h ={A \over V}\r \left( {l_z \over 2\p} \right)^2\]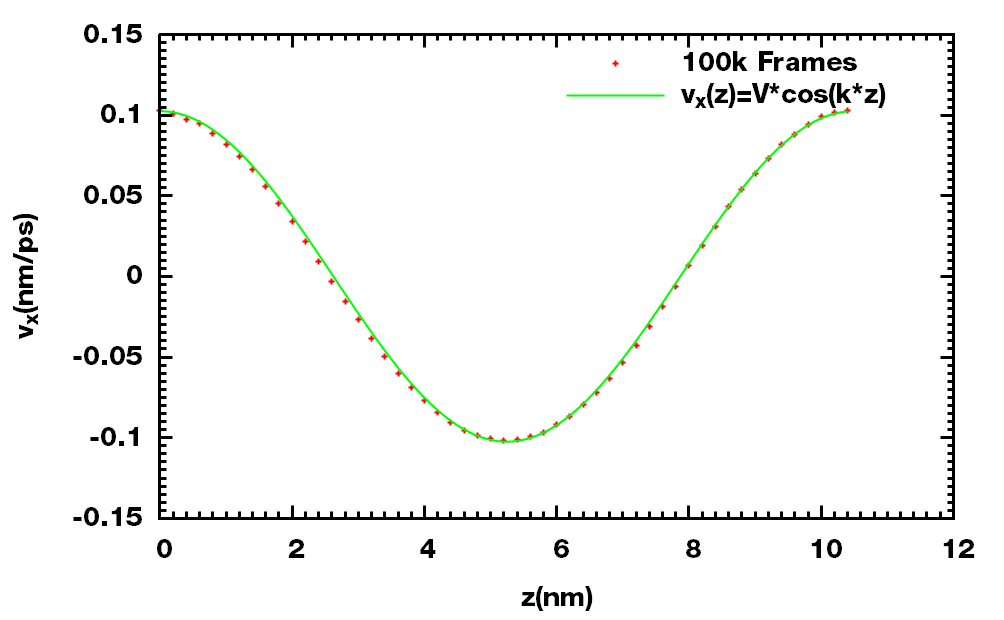

拟合得到V = 0.102462, k = 0.598828, 进而可计算出粘度

\[\h={\r A \over k^2 V}=0.6826 \ \text{mPa} \cdot \text{s}\]

与GROMACS给的数值相比, 差距不大.

此外, 在文献中还有对加速度振幅进行外推的处理方法, 供参考.

附: 模拟文件及命令

下载示例文件

模拟命令总结

gmx grompp -f em.mdp -o em.tpr
gmx mdrun  -v -deffnm em

gmx grompp -f npt1.mdp -c em.gro -o npt1.tpr
gmx mdrun  -v -deffnm npt1

gmx grompp -f npt2.mdp -c npt1.gro -o npt2.tpr
gmx mdrun  -v -deffnm npt2

gmx grompp -f nvt.mdp -c npt2.gro -o nvt.tpr
gmx mdrun  -v -deffnm nvt

gmx grompp -f vis.mdp -c nvt.gro -o vis.tpr
gmx mdrun  -v -deffnm vis

gmx trjconv -f vis.trr -s vis.tpr -o traj.gro
bash zvx.bsh