- 2021-11-06 23:16:43
gmx_puckering的背景说明见前一篇.
模拟流程
- 使用
AmberTools构建一个最简单的含两个糖环的多糖分子, 并输出Amber格式的拓扑和坐标 - 使用
acpype将Amber格式的坐标和拓扑转换为GROMACS格式 - 使用
gmx editconf -d 1将盒子修改为合适大小 - 为简单起见, 不填充溶剂, 只做真空中的NVT模拟, 这样环的构象变化快些, 多些
- 使用
gmx_puckering分析环构象
gmx_puckering分析环构象
gmx_puckering可分析单个环, 也可以同时分析多个环. 需要注意的是原子索引编号的排列顺序. 对五元环, 原子排列顺序必须是O2 C5 C4 C3 C2, 对六元环则是O5 C1 C2 C3 C4 C5. 如果名称不匹配, 程序会给出警告. 不同排列顺序是否影响结果, 待考.
下面是gmx_puckering的说明文档:
:-) gmx_puckering (-:
written 2007 by Oliver Stueker
revised 2021 by Jicun Li
GNU General Public License
DESCRIPTION
gmx_puckering is an analysis-tool for calculating the Cremer-Pople ring puckering
parameters of Pyranoses and Hexanoses within a given GROMACS trajectory file.
The index file needs to contain atom-sextuples or atom-quintuples in the order:
* O2 C5 C4 C3 C2 for Pyranoses, or
* O5 C1 C2 C3 C4 C5 for Hexanoses or
as defined by Cremer and Pople in
Cremer, D.; Pople, J. A., General definition of ring puckering coordinates,
J. Am. Chem. Soc. 1975, 97, (6), 1354-1358.
If the number of atoms in the group is not divisible by the ringsize give
by -i the program will give an Error and exit. The program will also chec
if the atomnames match to the scheme given above and give a warning if th
names don't match, which can be suppressed by using the -noname option.
Following plots are available:
-o cp_Q-theta-phi.xvg Q/Theta/Phi vs. Time
-otp cp_theta-phi.xvg Theta vs. Phi
-od cp_dtheta-dphi.xvg Distribution of Theta/Phi
-or cp_ring.xvg IUPAC Canonical Ring Conformation
Acknowledgments:
* GROMACS - http://www.gromacs.org
* g_puckering of Oliver Stueker - http://www.gromacs.org/Downloads/User_contributions/Other_software
* mdxvu of Mark J. Forster - http://sourceforge.net/projects/mdxvu/
Option Filename Type Description
------------------------------------------------------------
-s topol.tpr Input Structure+mass(db): tpr tpb tpa gro g96 pdb
xml
-f traj.xtc Input Generic trajectory: xtc trr trj gro g96 pdb
-n index.ndx Input Index file
-o cp_Q-theta-phi.xvg Output xvgr/xmgr file
-otp cp_theta-phi.xvg Output, Opt. xvgr/xmgr file
-od cp_dtheta-dphi.xvg Output, Opt. xvgr/xmgr file
-or cp_ring.xvg Output, Opt. xvgr/xmgr file
Option Type Value Description
------------------------------------------------------
-nice int 0 Set the nicelevel
-b time 0 First frame (ps) to read from trajectory
-e time 0 Last frame (ps) to read from trajectory
-dt time 0 Only use frame when t MOD dt = first time (ps)
-[no]w bool no View output xvg, xpm, eps and pdb files
-i int 6 Size of Ring
-[no]v bool no Be loud and noisy
-[no]dist bool yes Warn if distance between neighboring Ringatoms is
larger that 0.3 nm.
-[no]name bool yes Warn if Atomnames don't match with Definition by
Cremer & Pople.输出文件最多有4个,
cp_Q-theta-phi.xvg: CP坐标(Q, θ, φ)随时间变化图- ` cp_theta-phi.xvg`: (θ, φ)图, 或称极性图, 类似蛋白二级结果的拉氏图
cp_dtheta-dphi.xvg: θ和φ的分布图- ` cp_ring.xvg`: 环构象随时间变化的图
前3个文件的绘制无甚可言, 第4个环构象文件的绘制值得深入思考一下.
环构象数据的绘制
对于环构象随时间演化数据, 绘制其构象编号的演化可以, 但不直观. 绘制构象的名称, 类似蛋白二级结构图, 好些, 但仍不易识别各个构象之间的关系. 更好的方法是将其绘制在球面上, 因为三个CP坐标相当于球坐标. 但这样得到的图形是三维的, 在平面中展示不方便, 也会出现遮挡. 退而求其次, 可以考虑将球面展开, 绘制成平面图, 类似绘制世界地图的做法. 由于球面是不可展曲面, 展开成平面时必定存在变形, 所以需要考虑使用哪种投影. 常用的投影方法有很多种, 维基上有个列表, ArcGIS Pro的文档中也有一些说明.
最简单的方法, 直接以(θ,φ)作为平面坐标绘制, 相当于球半径无穷大时的情形. 这样失真最大, 无法感受各点之间的空间关系.
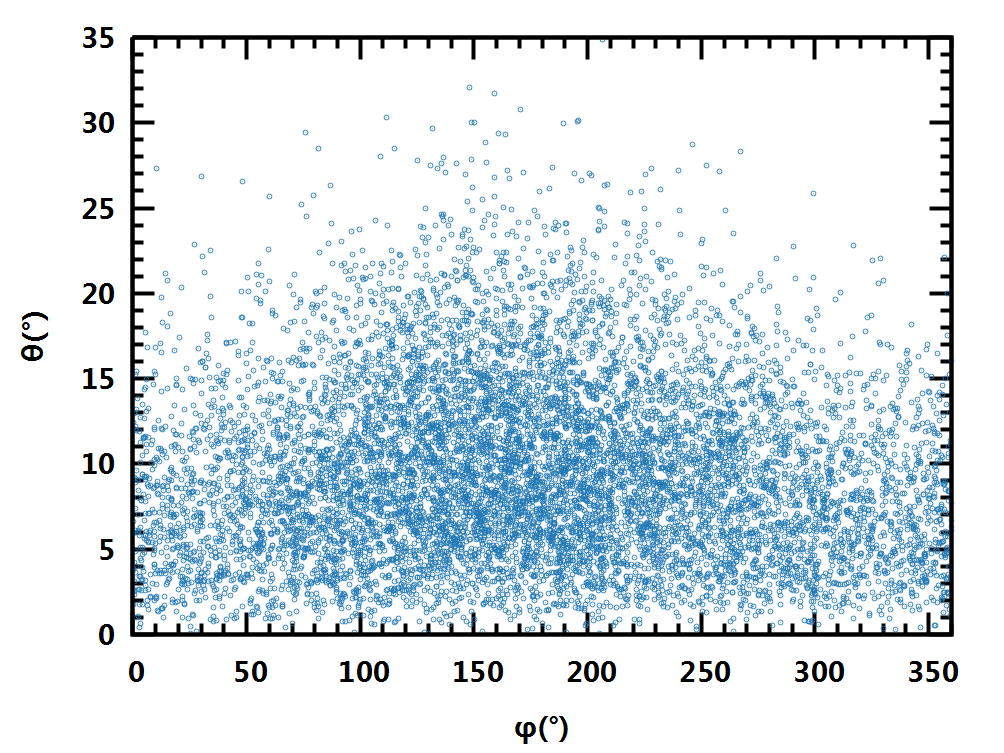
更高级点的投影方法, 各有侧重, 有的保持距离角度不变, 如Mercator投影, 方便用作航海图; 有的保持面积不变, 如Hammer-Aitoff投影, 正弦投影, 用作特定领域; 有的采取折衷方案, 尽量最小化各种偏差, 如Winkel三重投影, 可绘制通用地图. 这几种投影方法都有显式方程, 很方便使用.
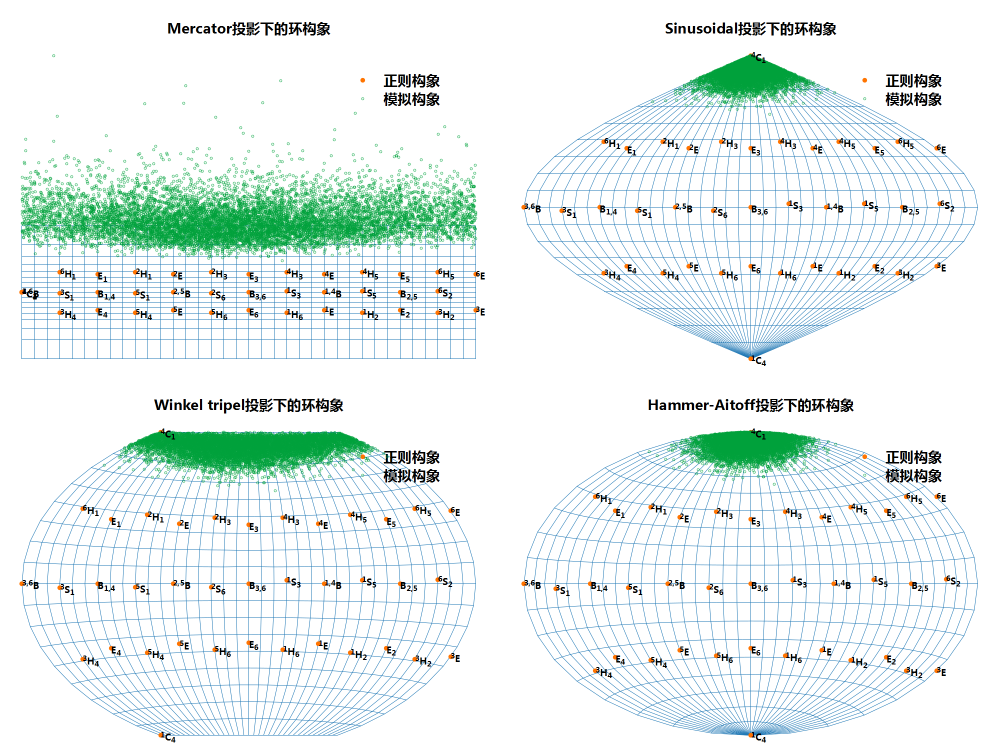
对比一下可看到, Hammer-Aitoff投影和正弦投影看起来效果更好些.
