哲●科●文Jerkwin 类别 标签 链接 关于 订阅

水溶液体系成笼分析程序cagen

类别: 科   标签: gmx 数理 编程   阅读次数:   版权: (CC) BY-NC-SA ✕

在对水溶液体系, 特别是气体水合物体系的模拟结果进行分析时, 常需要分析水分子借助氢键网络所形成的笼子. 甲烷水合物的常见构型sI, sII等就是以笼子形状区分的. 常见的相关模拟论文中通常会统计各种笼子数目与形态的变化. 目前我能查到的成笼分析程序有

其中GRADE是开源的, 其他程序要么不开源, 要么过于久远不易获得. 可惜的是GRADE只能识别几种常规的笼形(常见sI水合物为5¹²和5¹²-6², sII为5¹²和5¹²-6⁴). 实际应用中, 仅识别5, 6元环并不够, 总有其他各种奇形怪状的多面体值得研究, 一般需要识别4, 5, 6, 8元环及其组合. 然而要将GRADE代码扩展到能够识别任意笼形并不容易.

鉴于很多做水合物模拟的人需要进行成笼分析, 我就思考了一下这个问题, 得到了一些想法, 并初步编写了一个C++程序以验证想法的可行性.

定义分析问题

汝果欲学诗，工夫在诗外

我们先来考虑一下这个问题的定义. 处理任何问题的起点都是明确它的定义. 有些问题不易解决, 就在于没有良好定义. 良好地定义问题等于解决了问题的一半.

要进行成笼分析, 必须首先明确笼子的定义. 广义地说, 所谓笼子就是一个多面体区域, 由顶点, 边, 面等几何元素构成区域的内外分界面, 区域内部也可以存在一些东西. 这样定义的广义笼子最普遍通用, 但很难处理, 因为有太多可能性. 基于我们的目的, 可以将笼子定义得更狭义具体一些. 首先, 我们只考虑近似凸多面体, 因为非凸多面体更难处理, 数学上除了将其划分为更小的凸多面体外也没有太多处理办法. 其次, 我们不考虑复杂的笼子, 只考虑单笼, 即笼子只能相邻而不能互相嵌套穿插重叠. 一个笼子内部也不会包含其他笼子或者片段. 这样问题就简单了不少. 我们要找的笼子是凸多面体, 所以只要考虑由几个多边形封闭形成的空间即可. 为此, 我们可以首先找到各种多边形. 在此基础上, 根据边的相连接性拼合起来形成笼子.

接下来的问题是找多边形. 多边形是由几条边连接成的环, 所以要首先找到这些边, 然后根据边找到环, 形成多边形. 要找到边, 那首先需要定义顶点之间存在边的条件. 这样我们就将问题倒推到了要处理的最小元素–顶点. 解决问题的时候将这个过程反过来, 从顶点(原子)开始, 连点成边(键), 连边成面(多边形, 环), 连面成体(笼).

问题定义明确了, 下面就要看看能否将其化归为数学上已知的问题. 很多时候一些特定领域的问题都是数学上早已研究过并解决了的问题, 不需要重复发明更拙劣的轮子. 我们所考虑的这个要寻找顶点, 边, 面, 体的问题, 实际上是图论中的经典问题. 在图论中, 环也称为圈(cycle, loop), 无交叉的圈称为无弦圈(chordless cycle). 根据顶点连接关系找到圈的方法, 属于遍历问题, 采用深度优先搜索即可. 虽然也可以像GRADE那样采用多重循环的方法, 但代码写起来很麻烦, 也不好处理任意的多元环. 可以参考的资料罗列如下:

如何根据得到的多边形(环)组合得到多面体(笼子)是另一个难点. 目前文献上有两类方法. 一类是GRADE采用的cup方法或者其变体, 就是从一个环开始, 将与其有邻边的其他环拼接起来形成杯, 再由杯拼接成笼子. 这种方法容易理解, 处理起来却麻烦, 因为要根据环的连接信息和取向不断调整. 另一类方法是FSICA采用的遮掩方法, 简单说来就是将空间分格子, 得到很多格点, 以每个格点为起始点, 测试其周围是否存在笼子. 这类方法思路可取, 但做法过于简陋笨重, 找到的笼子也未必符合我们的要求. 我觉得除上述两类方法外还可以试试以下两类方法:

关于射线, 三角形相交的参考:

难点

可以想见的

代码

其流程如下

Windows下可执行程序及其测试文件见gmxtools.

使用说明

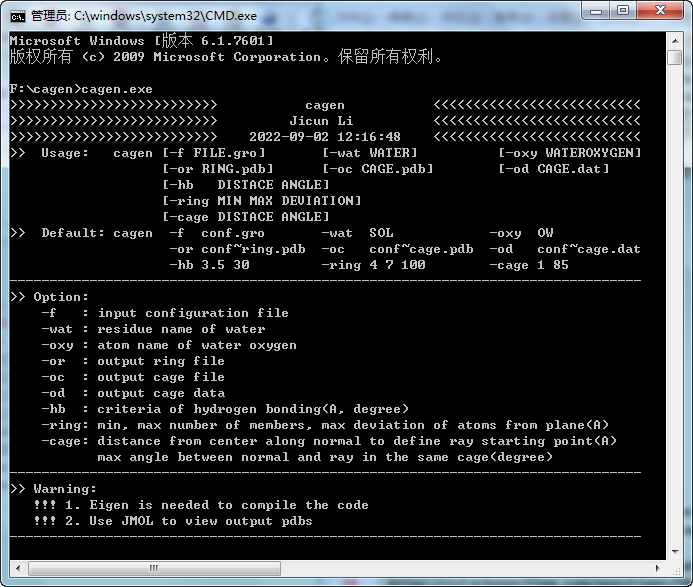
命令行选项:

示例

测试文件

测试结果

第1个测试文件 只含一个笼子5¹²-6⁴,

cagen -f conf1_512-64.gro
>>>>>>>>>>>>>>>>>>>>>>>>>>           cagen           <<<<<<<<<<<<<<<<<<<<<<<<<<
>>>>>>>>>>>>>>>>>>>>>>>>>>         Jicun Li          <<<<<<<<<<<<<<<<<<<<<<<<<<
>>>>>>>>>>>>>>>>>>>>>>>>>>    2022-09-02 12:16:48    <<<<<<<<<<<<<<<<<<<<<<<<<<
>>  Usage:   cagen [-f FILE.gro]       [-wat WATER]          [-oxy WATEROXYGEN]
				   [-or RING.pdb]      [-oc CAGE.pdb]        [-od CAGE.dat]
				   [-hb   DISTACE ANGLE]
				   [-ring MIN MAX DEVIATION]
				   [-cage DISTACE ANGLE]
>>  Default: cagen  -f  conf.gro       -wat  SOL            -oxy  OW
					-or conf~ring.pdb  -oc   conf~cage.pdb  -od   conf~cage.dat
					-hb 3.5 30         -ring 4 7 100        -cage 1 85
-------------------------------------------------------------------------------
>> Option:
	-f   : input configuration file
	-wat : residue name of water
	-oxy : atom name of water oxygen
	-or  : output ring file
	-oc  : output cage file
	-od  : output cage data
	-hb  : criteria of hydrogen bonding(A, degree)
	-ring: min, max number of members, max deviation of atoms from plane(A)
	-cage: distance from center along normal to define ray starting point(A)
		   max angle between normal and ray in the same cage(degree)
-------------------------------------------------------------------------------
>> Warning:
   !!! 1. Eigen is needed to compile the code
   !!! 2. Use JMOL to view output pdbs
-------------------------------------------------------------------------------

>>>> Settings
	 conf  File: conf1_512-64.gro
	 ring  File: conf~ring.pdb
	 cage  File: conf~cage.pdb
	 data  File: conf~cage.dat
	 water Name: SOL
	 OW    Name: OW
	 hb    Criteria: 3.5(A)  30(degree)
	 ring  Criteria: 4 7 100(A)
	 cage  Criteria: 1(A)  85(degree)
>>>> System
	 numAtom:  112
	 degree:   size=  112            capacity=  112
	 resName:  size=  112            capacity=  112
	 atmName:  size=  112            capacity=  112
	 atmXYZ:   size=  112    3       capacity=  112    3
	 isOW:     size=  112            capacity=  128
	 isEdge:   size=  112  112       capacity=  112  128
>>>> Water
	 OW:       28
	 numNode:  size=   28            capacity=   28
	 distRing: size=   28            capacity=   28
	 centRing: size=   28    3       capacity=   28    3
	 normRing: size=   28    3       capacity=   28    3
	 tangRing: size=   28    7   12  capacity=   28    7   12
	 nearRing: size=   28   28       capacity=   28   28
	 edgeList: size=  112            capacity=  112
	 ringList: size=   28   28       capacity=   28   28
	 cageList: size=   56   28       capacity=   56   28
	 cageNorm: size=   56            capacity=   56
>>>> Node degree:
>>>> Edge Size: 84
>>>> Edge Size (degree>1): 84
>>>> Find all Rings     Iter: 1601     Time(s): 0.002
	 Ring: 16
>>>> Ring Info.
	 numNode:  size=   16            capacity=   28
	 distRing: size=   16            capacity=   28
	 centRing: size=   16    3       capacity=   28    3
	 normRing: size=   16    3       capacity=   28    3
	 tangRing: size=   16    7   12  capacity=   28    7   12
	 nearRing: size=   16   16       capacity=   28   16
	 ringList: size=   16    6       capacity=   28    6
	 cageList: size=   32   16       capacity=   56   16
>>>> Fit Ring to Plane      Time(s): 0.002
	 Ring: 16
>>>> Neighbor all Rings     Time(s): 0.001
>>>> Write Rings to File
>>>> Determin Ring Occulasion     Time(s): 0
>>>> Conect Rings to Cage         Time(s): 0
	 Cages: 32
>>>> Deduplicate Cages            Time(s): 0
	 Cages: 1
>>>> Write Cages to File

识别笼型时先根据氢键判据确定两个水分子之间是否存在氢键, 再由此确定出所有可能的环(默认为4元环到7元环), 并拟合每个环平面的方程, 计算其法向, 以及环中原子偏离环平面的最大距离, 如果此最大距离小于设定值(默认100 Å), 则认为此环存在.

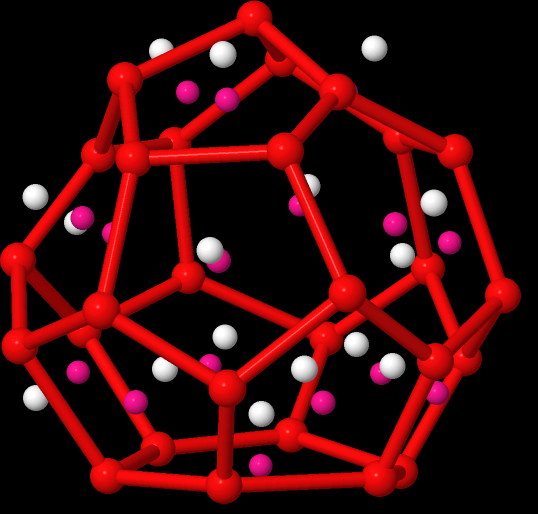
环构型输出文件中, 紫红原子对应环的中心, 白色原子对应环的法向, 由环中心出发的法线长度为1 Å(默认值).

以每个环的法线点为起始点, 向其他环中心连线, 如果此连线与法线的夹角小于85°(默认值), 则认为其他环可能处于同一笼中, 因此进行遮掩计算. 如果连线不会与任何一个环三角形相交, 且其他环与起始环可相连, 则它们处于同一笼中.

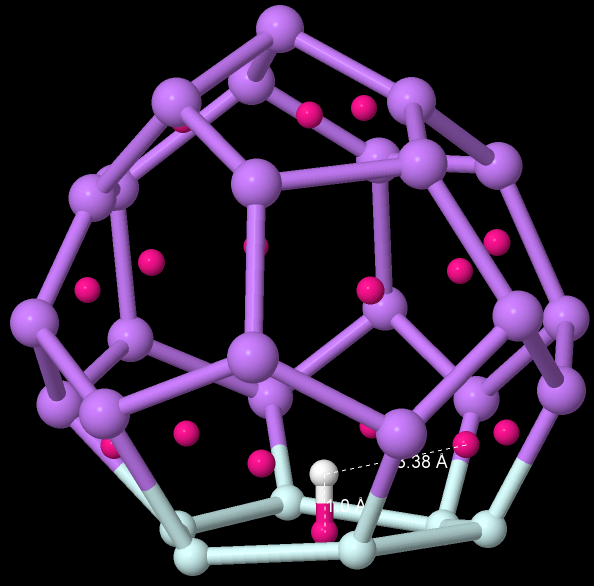
第7个测试文件 为甲烷与水的混合溶液, 基本相当于甲烷的水溶液, 使用默认条件识别的笼子很多, 且有些奇怪的笼子. 这说明单纯使用欧拉多面体公式作为封闭笼子的的判据有时并不够, 因为有些非凸的笼子也是符合这个公式的. 初步的处理方法是调整成环判据的偏离值, 剔除那些偏离平面过大的环.

第8个测试文件 为甲烷水合物, 使用默认条件识别的笼子并不多, 大部分都是比较常规的笼子.

待完善

◆本文地址: , 转载请注明◆
◆评论问题: https://jerkwin.herokuapp.com/category/3/博客, 欢迎留言◆
前一篇:　VMD的图形矩阵及其应用
后一篇:　关于分子动力学模拟的可重复性
访问人次(2015年7月 9日起): | 最后更新: 2024-11-01 02:53:58 UTC | 版权所有 © 2008 - 2024 Jerkwin 个