本手册已过时, 不再更新. 如果需要最新手册, 请加入下方QQ群.
- 3.1 简介
- 3.2 周期性边界条件
- 3.3 组的概念
- 3.4 分子动力学
- 3.5 壳层分子动力学
- 3.6 约束算法
- 3.7 模拟退火
- 3.8 随机动力学
- 3.9 Brown动力学
- 3.10 能量最小化
- 3.11 简正模式分析
- 3.12 自由能计算
- 3.13 副本交换动力学
- 3.14 主成分动力学抽样
- 3.15 扩展系综动力学
- 3.16 并行
- 3.17 区域分解
- 3.18 隐式溶剂模型
3.1 简介
在本章中, 我们首先介绍GROMACS用到的一些基本概念: 周期性边界条件 (3.2节)和 组 (3.3节). MD算法将在3.4节介绍: 首先给出算法的整体形式, 然后在后面的小节中进行详细说明. (简单的)EM(Energy minimization, 能量最小化)算法在3.10节说明. 用于特殊目的动力学的一些其他算法在此后进行说明.
有几个问题是人们普遍关心的. 在所有情况下, 必须定义由分子组成的 体系. 而分子又是由定义了相互作用形式的粒子组成. 关于分子 拓扑结构 和 力场 的详细描述以及力的计算将在第四章讨论. 在本章中, 我们只讨论算法的其他方面, 如配对列表(pair list)的生成, 速度和位置的更新, 与外部温度和压力的耦合, 约束的保持. 对MD模拟数据的 分析 将在第八章讨论.
3.2 周期性边界条件
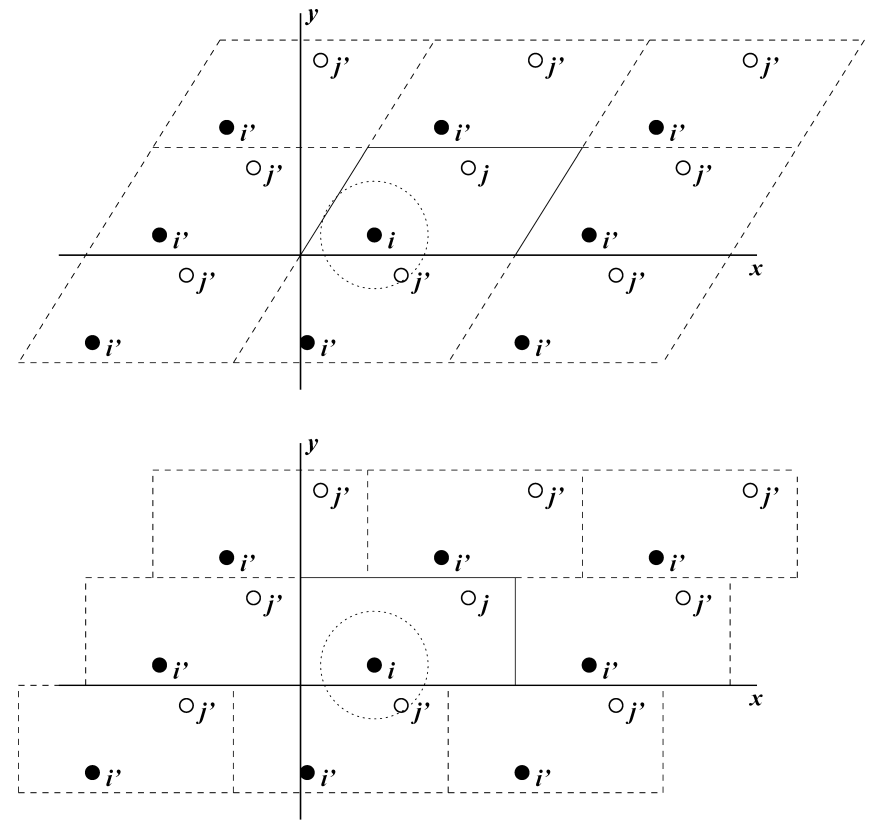
对有限的体系, 减小边缘效应的经典方法是应用 周期性边界条件. 将待模拟体系的原子放到一个空间填充(space-filling)的盒子中, 周围是体系自身平移后的副本(图 3.1). 因此, 体系不存在边界, 由孤立团簇的多余边界导致的问题现在被由周期性条件引起的问题所取代. 如果体系具有晶体结构, 这样的边界条件符合预期(尽管运动自然被限制于周期性运动, 且其波长与盒子适应). 如果希望模拟非周期性体系, 如液体或溶液, 周期性就会带来误差. 此误差可以通过比较不同尺寸体系的模拟结果进行评估. 比起由不自然的真空边界引起的误差, 周期性边界引起的误差更小一些.
用于空间填充的元胞的有几种可能的形状. 其中的一些, 如 菱形十二面体 与 截角八面体 [18]比立方体更接近于球形, 并因此更适合用于研究溶液中近似球形的大分子, 这是由于对给定的大分子映像的最小距离, 填充这两种形状的盒子需要的溶剂分子更少. 同时, 菱形十二面体和截角八面体是 三斜晶胞 的特殊情况, 而三斜晶胞是最一般的空间填充元胞, 组成了所有可能的空间填充形状[19]. 出于这个原因, GROMACS是基于三斜晶胞的.
GROMACS使用周期性边界条件, 并结合了 最小映像约定: 对短程非键相互作用, 每个粒子只考虑它的一个最近的映像. 对长程静电相互作用, 这有时不够准确, 因此GROMACS还采用了点阵加和的方法, 如Ewald加和, PME和PPPM.
GROMACS支持任何形状的三斜盒子. 模拟盒(元胞)由3个盒矢量 \(\mathbf{a,b,c}\) 定义. 盒矢量必须满足以下条件:
\[a_y=a_z=b_z=0 \tag{3.1}\]
\[a_x > 0, \; b_y > 0, \; c_z > 0 \tag{3.2}\]
\[\abs{b_x} \le {1\over2} a_x, \; |c_x| \le {1\over2} a_x, \; |c_y| \le {1\over2} b_y \tag{3.3}\]
通过旋转盒子, 总可以使得等式3.1成立, 不等式(3.2)和(3.3)也总可以通过增减盒矢量使其成立.
即便使用三斜盒子进行模拟, 为了提高计算效率, GROMAC始终将粒子放在长方体空间内, 对二维体系的图示见图3.1. 因此, 从输出的轨迹来看, 模拟好像是在长方体盒子中进行的. trjconv程序可用于转换轨迹, 以便在不同的元胞中显示.
模拟时也可不使用周期性边界条件, 但当模拟孤立的分子团簇时, 使用一个很大的周期性盒子通常效率更高, 这是因为快速的格点搜索只能在周期性体系中使用.
| 盒子类型 | 映像距离 | 盒子体积 | 盒矢量 abc | 盒矢量夹角 |
|---|---|---|---|---|
| 立方 | \(d\) | \(d^3\) | \(d\) 0 0 0 \(d\) 0 0 0 \(d\) |
\(90^{\circ}\) \(90^{\circ}\) \(90^{\circ}\) |
| 菱形十二面体(XY-正方) | \({1\over2}\sqrt2 d^3\) \(0.707d^3\) |
\(d\) 0 \({1\over2}d\) 0 \(d\) \({1\over2}d\) 0 0 \({1\over2}\sqrt2 d\) |
\(60^{\circ}\) \(60^{\circ}\) \(90^{\circ}\) | |
| 菱形十二面体(XY-六角) | \(d\) \({1\over2}d\) \({1\over2}d\) 0 \({1\over2}\sqrt3 d\) \({1\over6}\sqrt3 d\) 0 0 \({1\over3}\sqrt6 d\) |
|||
| 截角八面体 | \({4\over9}\sqrt3 d^3\) \(0.770 d^3\) |
\(d\) \({1\over3}d\) -\({1\over3}d\) 0 \({2\over3}\sqrt2 d\) \({1\over3}\sqrt2 d\) 0 0 \({1\over3}\sqrt6 d\) |
\(71.53^{\circ}\) \(109.47^{\circ}\) \(71.53^{\circ}\) |
3.2.1 一些有用的盒子类型
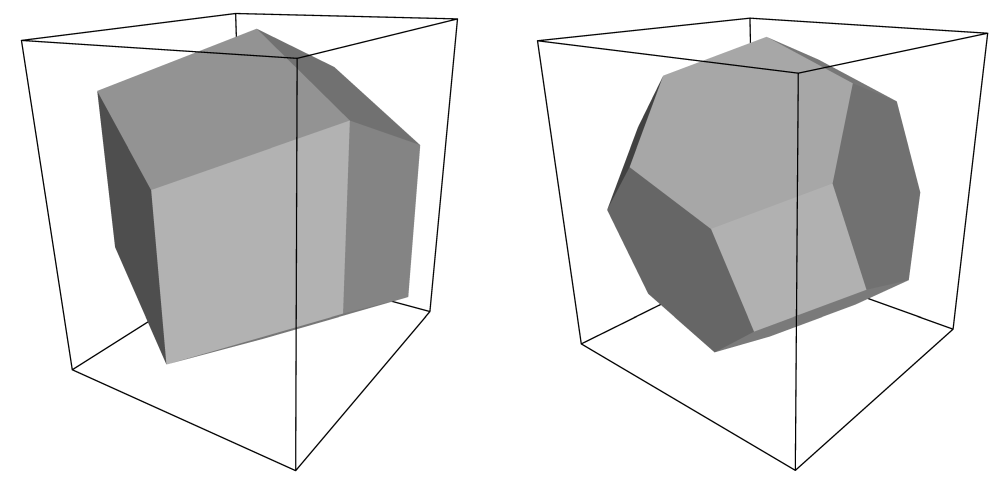
表3.1列出了用于模拟溶液体系的三种最常用的盒子类型. 菱形十二面体(图3.2)是最小, 最规则的空间填充元胞. 12个映像元胞的每一个具有相同的距离, 其体积是具有相同映像距离的立方体体积的71%. 当模拟溶液中球形或柔性的分子时, 这样可以节省约29%的CPU时间. 有两种不同取向的菱形十二面体满足方程3.1, 3.2和3.3. 程序editconf生成与xy平面有正方截面的菱形十二面. 之所以选择这个取向, 是因为该取向的菱形十二面的前两个盒矢量与x轴和y轴重合, 因此容易理解. 另一取向可用于膜蛋白的模拟. 这时它在xy平面的截面是一个六边形, 其面积比具有相同的映像距离的正方形的面积小14%. 为获得最佳间距, 可以改变盒子的高度(\(c_z\)). 这种盒子形状不仅可以节省CPU时间, 也可以使蛋白质的分布更加均匀.
3.2.2 截断限制
最小映像约定意味着, 用于截断非键相互作用的截断半径不能超过最短盒矢量的一半:
\[R_c < {1\over2} \text{min} (\lVert \mathbf a \rVert, \lVert \mathbf b\rVert, \lVert \mathbf c\rVert) \tag{3.4}\]
否则将会有多个映像出现在力的截断距离内. 当研究溶液中的大分子——如蛋白质——时, 仅考虑这个限制是不够的: 原则上, 单个的溶剂分子应该无法同时“看到”大分子的两侧. 这意味着, 每个盒矢量的长度都必须超过大分子在该方向的长度 再加上 两倍的截断半径 \(R_c\). 但人们经常不严格遵守这个限制, 以便稍微减少溶剂层从而节约计算成本. 出于效率的考虑, 三斜盒子的截断更受限制. 对格点搜索的额外限制弱一些:
\[R_c < \text{min}(a_x, b_y, c_z) \tag{3.5}\]
对简单搜索的额外限制更强:
\[R_c < {1\over2} \text{min}(a_x, b_y, c_z) \tag{3.6}\]
每个元胞(立方, 长方或三斜)都被26个平移的映像所包围. 因此一个特定的映像始终可以用指向27个 平移矢量 之一的索引来指认, 并通过对索引矢量进行平移来构建(见3.4.3). 约束式(3.5)保证了只需要考虑26个映像.
3.3 组的概念
GROMACS的MD和分析程序可对用户自定义的原子 组 进行一些操作. 组的最大数目为256, 但每个原子最多只能属于六类不同的组. 这六类组如下:
温度耦合组 对每个温度耦合组可单独定义温度耦合参数(参考温度, 时间常数, 自由度数目, 参见3.4.4). 例如, 在高分子溶液中, 相比高分子, 溶剂分子(力和积分的误差使其容易产生更多热效应)可以使用更短的时间常数与热浴耦合, 又如, 可以将表面的温度维持得低于比吸附分子的温度. 可以定义许多不同的温度耦合组. 也请参看下面质心组.
冻结组 属于冻结组的原子在模拟过程中始终保持静止. 在平衡体系的过程中这是很有用的, 例如, 可避免不当放置的溶剂分子对蛋白质的原子产生不合理的碰撞, 尽管对受保护原子添加约束势可以得到同样的效果. 如果需要, 冻结选项可仅仅用于原子的一个或两个坐标, 从而将原子冻结在一个平面或一条直线上. 当一个原子被部分冻结时, 它所受约束仍然可以使它移动, 即便是在冻结方向上. 一个被完全冻结的原子不能被它所受的约束移动. 可定义许多冻结组. 冻结坐标不受压力缩放影响;在某些情况下, 这可能会产生无用的结果, 尤其是与约束同用时(在这种情况下, 你会得到非常大的压力). 因此, 我们建议避免将冻结组与约束和压力耦合混合使用. 为了平衡体系, 可以先在使用冻结进行等体积模拟时, 然后再使用位置约束与恒压模拟.
加速组 加速组的每个原子上会被加上一个加速度 \(\bi a^g\), 这等同于受到一个外力. 利用这个特性可驱使体系进入非平衡态, 并进行非平衡MD模拟以计算输运性质.
能量监测组 在模拟中, 所有能量监测组之间的交叉相互作用都会被考虑, 且对Lennard-Jones项和库仑项的计算是分开进行的. 原则上, 最多可定义256组, 但这样将会计算256×256项相互作用!最好保守地使用.
能量监测组之间的所有非键相互作用都可以被排除在外(参见7.3节). 在能量监测组中被排除的粒子对不会被放入配对列表, 当不需要计算体系中的某些相互作用时, 这样做可以显著提高模拟速度.
质心组 GROMACS可以移除质心(center of mass, COM) 的运动, 无论是整个体系的质心还是或原子组的质心. 后者(移除原子组的质心)是有用的, 比如, 对于存在有限的阻止质心运动的摩擦的体系(如气体体系). 对温度耦合与质心运动移除使用相同的组是合理的.
压缩位置输出组 为了进一步减小压缩轨迹文件(.xtc或.tng)的大小, 可以仅仅存储一部分粒子的轨迹. 所有标记为压缩组的会被保存, 其他则不会. 如果没有指定这样的输出组, 所有的原子坐标都将被保存到压缩轨迹文件.
GROMACS工具中组的使用将在8.1节详述.
3.4 分子动力学
MD的整个流程见图3.3. 每次运行MD或EM都需要体系中所有粒子一组初始坐标和(可选的)初始速度作为输入. 本章不介绍如何获得它们; 对于如何设置并实际运行MD, 请参考www.gromacs.org上的在线手册.

3.4.1 初始条件
拓扑和力场
必须读入体系的拓扑, 它包含了对力场的说明. 力场和拓扑将分别在第四章和第五章进行说明. 所有这些信息都是固定的, 在运行过程中始终不变.
坐标和速度
然后, 在开始运行前, 需要知道盒子的尺寸, 所有粒子的坐标和速度. 盒子的尺寸和形状是由三个矢量(9个数字) \(\bi b_1, \bi b_2, \bi b_3\) 决定的, 它们代表了周期性盒子的三个基矢量.
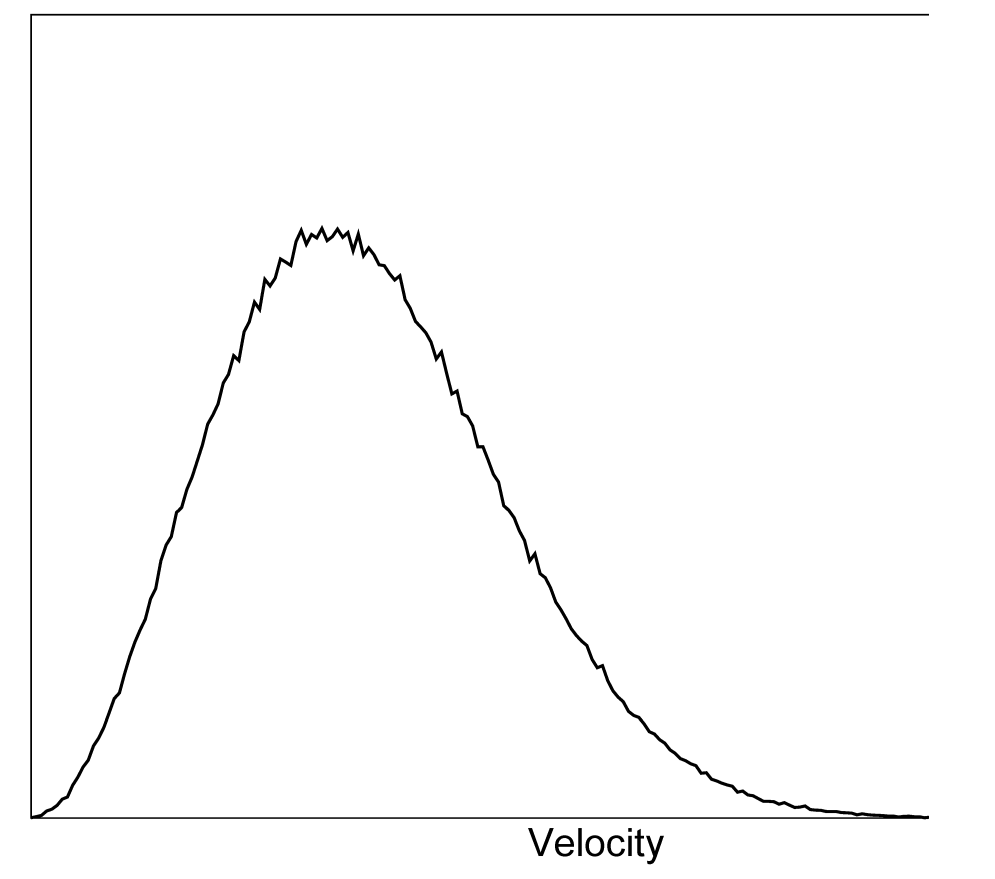
如果从 \(t=t_0\) 开始运行, 必须知道 \(t=t_0\) 时刻的坐标. 如果以 \(\D t\) 为时间步长, 使用默认的 蛙跳式算法 更新时间步(参见3.4.4节), 还需要知道 \(t=t_0-{1\over2}\D t\) 时刻的速度. 如果没有可用的速度, 程序可以根据给定的绝对温度 \(T\) 产生所需要的初始原子速度 \(v_i, i=1 ... 3N\) (图3.4):
\[p(v_i)=\sqrt{ {m_i \over 2\p kT } } \exp\left(-{m_iv_i^2 \over 2kT} \right) \tag{3.7}\]
其中 \(k\) 为玻耳兹曼常数(见第二章). 为此, 会使用产生12个随机数 \(R_k\), \(0 \le R_k < 1\) 并从其和中减去6的方法来产生服从正态分布的随机数. 结果会乘上速度分布的标准偏差 \(\sqrt{kT/m_i}\). 因为由此得到的总能量不会精确地对应于所需的温度 \(T\), 需要进行校正: 首先移除质心的运动, 然后再对所有的速度进行缩放, 以使总能量恰好对应于 \(T\)(参见公式3.18).
质心运动
正常情况下, 在每一步中都会将质心的速度设置为零, 体系(通常)不受净的合外力作用, 其质心速度应该保持不变. 然而在实际中, 更新算法会导致质心速度发生缓慢的变化, 并因此使得体系的总动能发生变化, 特别是使用温度耦合时. 如果不对这种变化进行处理, 长时间后质心会有明显的运动, 温度也出现显著异常. 体系的整体转动也会导致同样的问题, 但只出现在孤立团簇的模拟中. 在填满盒子的周期性体系中, 整体转动会与其它自由度耦合, 不会导致这个问题.
3.4.2 近邻搜索
正如在第四章提到的, 内力或者由固定(静态)列表产生, 或者由动态列表产生. 后者包含了任意粒子对之间的非键相互作用. 当计算非键力时, 将所有粒子置于长方体盒子中计算更容易. 如图3.1所示, 可以通过一定的方法将三斜盒转换为长方盒. 所以GROMACS的输出坐标总是处于一个长方盒中, 即使模拟时使用了十二面体盒子或三斜盒子. 方程3.1保证了我们可以通过如下方法重置粒子使其处于长方盒中: 先沿盒矢量 \(\bi c\) 移动, 再沿 \(\bi b\) 移动, 最后沿 \(\bi a\) 移动. 根据三个限制性方程3.3, 3.4和3.5, 我们可以利用不超过一倍盒矢量的线性组合找到14个最近的三斜盒子映象.
配对列表的生成
只需要对一些粒子对 \(i, j\) 之间的非键配对力进行计算, 在这些粒子对中, 粒子 \(i\) 和 \(j\) 的最近映象之间的距离 \(r_{ij}\) 小于给定的截断半径 \(R_c\). 如果彼此之间的相互作用已完全被键合作用所考虑, 一些满足这一条件的粒子对仍然会被排除. GROMACS使用了一个 配对列表, 其中包含了那些必须计算彼此之间非键力的粒子对. 这个列表中包含原子 \(i\), 原子 \(i\) 的位移向量, 距离原子 \(i\) 的这个特殊映象rlist范围内的所有粒子 \(j\). 该列表每nstlist步更新一次, nstlist的典型值为10. 有一个选项可用来计算每个粒子所受到的总的非键力, 这些力来源于围绕列表截断值, 即距离在rlist和rlistlong之间的壳层中的所有粒子. 在更新配对列表时, 会计算这些力, 并在随后的nstlist中保持不变.
为创建邻区列表, 必须找到与给定粒子相近(即在邻居列表截断内)的所有粒子. 这种搜索通常被称为邻区搜索(NS, neighbor search)或对搜索(pair search), 涉及到周期性边界条件和映象的确定(参见3.2节). 搜索算法的复杂度为 \(O(N)\), 尽管更简单的 \(O(N^2)\) 算法在一定条件下仍然可用.
邻区截断方案: 原子组与Verlet缓冲
从4.6版本开始, GROMACS支持两种不同的截断方案设置: 最初的基于原子组的方案和使用Verlet缓冲区的方案. 它们之间存在一些非常重要的区别, 这些区别可能会影响计算结果, 计算性能和某些功能的支持情况. 组方案(几乎)可以像Verlet方案一样运行, 但这将导致性能降低. 对在模拟中常用的水分子, 组方案特别快, 但在最近的x86处理器中, 这种优势消失了, 因为可以在Verlet方案的实现中使用更好的指令级并行. 在5.0版本中已经不再提倡使用组方案了, 将来的版本中将会删除此方案.
在组方案中, 近邻列表由至少含一个原子的原子对构成. 这些原子组最初是电荷组(参见3.4.2节), 但对长程静电进行了妥善处理, 性能是它们唯一的优势. 几何中心在截断距离内的两个组会被放入近邻列表中. 在一定数目的MD模拟步中, 会计算所有原子对(每个电荷组一个)之间的相互作用力, 直到下一次更新近邻列表. 这种设置高效, 因为近邻搜索只检查电荷组对, 而不是原子对(对三原子水模型可节约 \(3\times 3=9\) 倍), 而且还可以优化非键合力的计算内核, 比如说一个水分子“组”. 没有明确的缓冲时, 由于一些原子对处于截断距离之内却没有相互作用, 而一些原子对处于截断距离之外却有相互作用, 这种设置会导致能量的漂移. 可能有以下原因:
- 原子在两次近邻搜索之间穿过了截断区域, 和/或
- 对包含一个以上原子的电荷组, 当电荷组的几何中心移动到截断距离以外/内时, 会导致一部分原子对移动到截断距离以内/外.
显式地为近邻列表增加一个缓冲会消除这些问题, 但这需要较高的计算成本. 问题的严重程度取决于体系, 你感兴趣的性质, 以及截断距离的设置.
Verlet截断方案默认使用缓冲对列表. 它也使用了原子团簇, 但这些不像在组方案中是静态的. 相反, 团簇以空间定义, 包含4个或8个原子, 使用如SSE, AVX和GPU的CUDA等可方便地对此进行流计算. 在近邻搜索步骤中, 使用Verlet缓冲创建对列表, 即对列表的截断距离大于相互作用的截断距离. 在计算非键力的内核中, 只有当一个原子对在特定时间步处于截断距离之内时, 这个力才会被加入到近邻列表中. 当原子在两次对搜索步骤中移动时, 这确保了几乎所有处于截断距离内的原子之间的力都会被计算. 我们说, 几乎 所有的原子, 是因为GROMACS使用了一个固定的对列表更新频率以提高效率. 一个处于截断距离外的原子对, 在这样固定的步数中, 可能移动得足够多以致处于截断距离之内. 这种小概率事件会导致小的能量漂移, 而且概率的大小取决于温度. 当使用温度耦合时, 给定能量漂移的一定容差, 可以自动确定缓冲大小.
在mdp文件中Verlet方案的设置为:
cutoff-scheme = Verlet
Verlet-buffer-tolerance = 0.005
Verlet缓冲的大小由后一选项决定, 这里使用了默认设置: 在一对原子中每个原子的能量误差为0.005 kJ/mol/ps. 需要注意的是, 在配对能量的误差会相互抵消, 这对总能量漂移的影响通常至少比容差小一个数量级. 此外, 总能量的漂移受许多其他因素影响, 通常, 来自约束算法的贡献占主导地位.
对等能量(NVE)模拟, 缓冲大小由对应于速度(无论由何种合适的方法产生, 或由输入文件提供)的温度来决定. 此外, 容差可以设置为–1, 并手动指定缓冲: rlist > max(rcoulomb, rvdw). 得到合理缓冲大小的最简单方法是: 利用NVT的mdp文件并将目标温度设定为NVE模拟中你希望使用的温度, 然后将grompp打印出的缓冲大小移植到NVE的mdp文件中.
基于粒子团簇实现的Verlet截断方案非常高效. 最简单的例子是包含4个粒子的团簇. 然后基于团簇对构建对列表. 团簇对搜索比基于粒子对的搜索快得多, 因为一次可以将 \(4 \times 4= 16\) 个粒子置于列表中. 然后就可以一次计算这16个粒子对之间的非键相互作用, 这可以很好地映射到SIMD单元, 它一次可以执行多个浮点运算(例如基于SSE, AVX, GPU的CUDA, BlueGene FPUs). 在绝大多数类型的体系中, 这种非键相互作用的计算内核要比组方案的内核快很多, 除了在短SIMD宽度的处理器上, 对水分子不使用缓冲对列表时. 后者在(生物)分子模拟中很常见, 所以为了达到最快速度, 值得比较两种方案的性能.
由于Verlet截断方案在4.6版本的GROMACS中才推出, 所以它并不支持组方案中的所有功能. Verlet截断方案支持一些组方案不支持的功能, 表3.2给出了两种截断方案中不(完全)支持的功能.
| 非键相互作用特性 | 组 | Verlet | |
|---|---|---|---|
| 无缓冲截断方式 | √ | 非默认 | |
| 精确截断 | 移位/切换 | √ | |
| 移位相互作用 | 力+能量 | 能量 | |
| 切换势能 | √ | √ | |
| 切换力 | √ | √ | |
| 非周期性体系 | √ | Z+墙 | |
| 隐式溶剂 | √ | ||
| 自由能微扰的非键相互作用 | √ | √ | |
| 组能量贡献 | √ | CPU(而非GPU) | |
| 能量组排除 | √ | ||
| AdResS多尺度 | √ | ||
| OpenMP多线程 | 仅PME | √ | |
| GPU原生支持 | √ | ||
| Lennard-Jones PME | √ | √ | |
能源漂移与对列表缓冲
对于一个正则系综(NVT), 由有限的Verlet缓冲大小所造成的平均能量误差, 可以由截断处的原子位移和势能形状来确定. 在温度 \(T\) 下, 一个质量为 \(m\) 的自由粒子, 其一维方向上的位移在时间 \(t\) 内的分布为高斯分布, 均值为0, 方差为 \(\s^2=tk_BT/m\). 对两个原子之间的距离, 其方差变为 \(\s^2 = \s_{12}^2 = t k_B T(1/m_1 +1/m_2)\). 注意, 在实际过程中, 时间 \(t\) 内粒子通常还会与其他粒子相互作用, 所以实际的位移分布会窄得多. 给定非键相互作用的截断距离 \(r_c\), 对列表截断距离 \(r_l=r_c+r_b\). 当类型为1的粒子被数密度为 \(\r_2\) 的粒子类型2包围, 粒子间距从 \(r_0\) 变到 \(r_t\) 时, 我们可以得到在时间 \(t\) 之后1和2两种类型的粒子之间的相互作用的平均能量误差:
\[\alg \langle \D V \rangle & = \int_0^{r_c} \int_{r_l}^\infty 4 \p r_0^2 \r_2 V(r_t)G\left({r_t-r_0 \over \s} \right) \rmd {r_0} \rmd{r_t} \tag{3.8} \\ & \approx \int_{-\infty}^{r_c} \int_{r_l}^\infty 4 \p r_0^2 \r_2 \bigg[ V'(r_c)(r_t-r_c)+ \\ &\phantom{\approx \int_{-\infty}^{r_c} \int_{r_l}^\infty 4 \p r_0^2 \r_2 \bigg[{}\ } V''(r_c){1\over2}(r_t-r_c)^2 \bigg] G\left({r_t-r_0 \over \s}\right) \rmd {r_0} \rmd{r_t} \tag{3.9} \\ & \approx 4\p(r_l+\s)^2 \r_2 \int_{-\infty}^{r_c} \int_{r_l}^\infty \bigg[ V'(r_c)(r_t-r_c)+ \\ &\phantom{\approx 4\p(r_l+\s)^2 \r_2 \int_{-\infty}^{r_c} \int_{r_l}^\infty \bigg[{}\ } V''(r_c){1\over2}(r_t-r_c)^2 + \\ &\phantom{\approx 4\p(r_l+\s)^2 \r_2 \int_{-\infty}^{r_c} \int_{r_l}^\infty \bigg[{}\ } V'''(r_c){1\over6}(r_t-r_c)^3 \bigg] G\left({r_t-r_0 \over \s}\right) \rmd {r_0} \rmd{r_t} \tag{3.10} \\ & = 4\p(r_l+\s)^2 \r_2 \bigg\{ {1\over2} V'(r_c) \left[ r_b \s G\left(r_b\over\s\right)-(r_b^2+\s^2)E\left(r_b\over\s\right) \right] + \\ &\phantom{= 4\p(r_l+\s)^2 \r_2 \bigg\{ {}\ } {1\over6} V''(r_c) \left[ \s(r_b^2+2\s^2) G\left(r_b\over\s\right)-r_b(r_b^2+3\s^2)E\left(r_b\over\s\right) \right] + \\ &\phantom{= 4\p(r_l+\s)^2 \r_2 \bigg\{ {}\ } {1\over24} V'''(r_c) \left[ r_b\s(r_b^2+5\s^2) G\left(r_b\over\s\right)-(r_b^4+6r_b^2\s^2+3\s^2)E\left(r_b\over\s\right)\right] \bigg\} \tag{3.11} \ealg\]
其中 \(G\) 为零均值单位方差的高斯分布, \(E(x)={1\over2}\text{erfc}(x/\sqrt 2)\). 我们总是希望得到的误差很小, 所以 \(\s\) 比 \(r_c\) 和 \(r_l\) 都小, 这样上述方程中的近似很好, 因为高斯分布衰减很快. 能量误差需要对所有粒子对类型进行平均, 并对粒子数进行加权. 在GROMACS中我们不允许粒子对类型之间的误差抵消, 所以我们对绝对值进行平均. 为获得单位时间的平均能量误差, 需要将平均能量误差除以近邻列表时间长度 \(t=(\text{nslist}-1)\times \text{dt}\). 此函数不能解析地得到, 因此对给定的目标漂移, 我们使用二分法来获得缓冲大小 \(r_b\). 我们还注意到, 在实际中误差通常比这里估计的小很多, 如凝聚相中粒子的位移会比自由移动粒子的位移小得多, 这里使用了这个假定.
当存在(键)约束时, 一些粒子的自由度会变少. 这会减少能量误差. 一个具有两个自由度的粒子任意方向上的位移并不是高斯分布, 而是服从余误差函数:
\[{\sqrt \p \over 2\sqrt 2 \s} \text{erfc}\left({|r| \over \sqrt 2 \s} \right) \tag{3.12}\]
其中 \(\s^2\) 为 \(k_BT/m\). 没有办法解析地对此分布进行积分以获得能量误差. 但我们可以使用缩放和移位高斯分布来得到紧上界(这里未给出). 这种高斯分布可用于计算能量误差, 如上所述. 现在我们来考虑约束粒子, 即具有2个或更少自由度的粒子, 它们通过约束连接到其他粒子上, 其他粒子的总质量至少为约束粒子本身质量1.5倍. 对具有单个约束的粒子, 沿约束方向的总质量至少是2.5倍, 这样沿约束方向的位移方差至少减少为原来的1/6.25. 由于高斯分布衰减非常迅速, 这有效地移除了来自位移的一个自由度. 多重约束会减少更多位移, 但因为会变得非常复杂, 我们将那些粒子视为只有2个自由度的粒子.
还有一个重要的实现细节, 可减少因有限的Verlet缓冲列表大小造成的能量误差. 上述推导假定了粒子对列表. 然而, GROMACS实现时使用了团簇对列表以提高效率. 在大多数情况下, 对列表包含4个粒子组成的团簇之间的对, 也称为 \(4\times4\) 列表, 但也可以是 \(4\times8\)(GPU CUDA内核和AVX 256位单精度内核)或 \(4\times2\)(SSE双精度内核). 这意味着对列表比相应的 \(1\times1\) 列表高效得多. 这样稍微超出对列表截断时, 列表中仍然会有一大部分粒子. 这些粒子所占的总粒子的分数可以在模拟中确定, 并精确地根据一些合理的假设进行估计. 随着对列表范围的增加, 这些粒子分数减小, 意味着可以使用较小的缓冲. 对于典型的全原子模拟, 使用0.9 nm截断, 这个分数大约是0.9, 可使能量误差减少到原来的1/10. 在自动Verlet的缓冲计算时考虑了这种减少, 这样得到的缓冲尺寸较小.
由图3.5可以看出, 对小的缓冲大小, 由于误差抵消, 总能量漂移比对能量误差容差小得多. 对于较大的缓冲大小, 误差估计比总能量漂移高6倍, 或者缓冲估计大0.024 nm. 这是因为质子自由移动不能超过18 fs, 但振动可以.
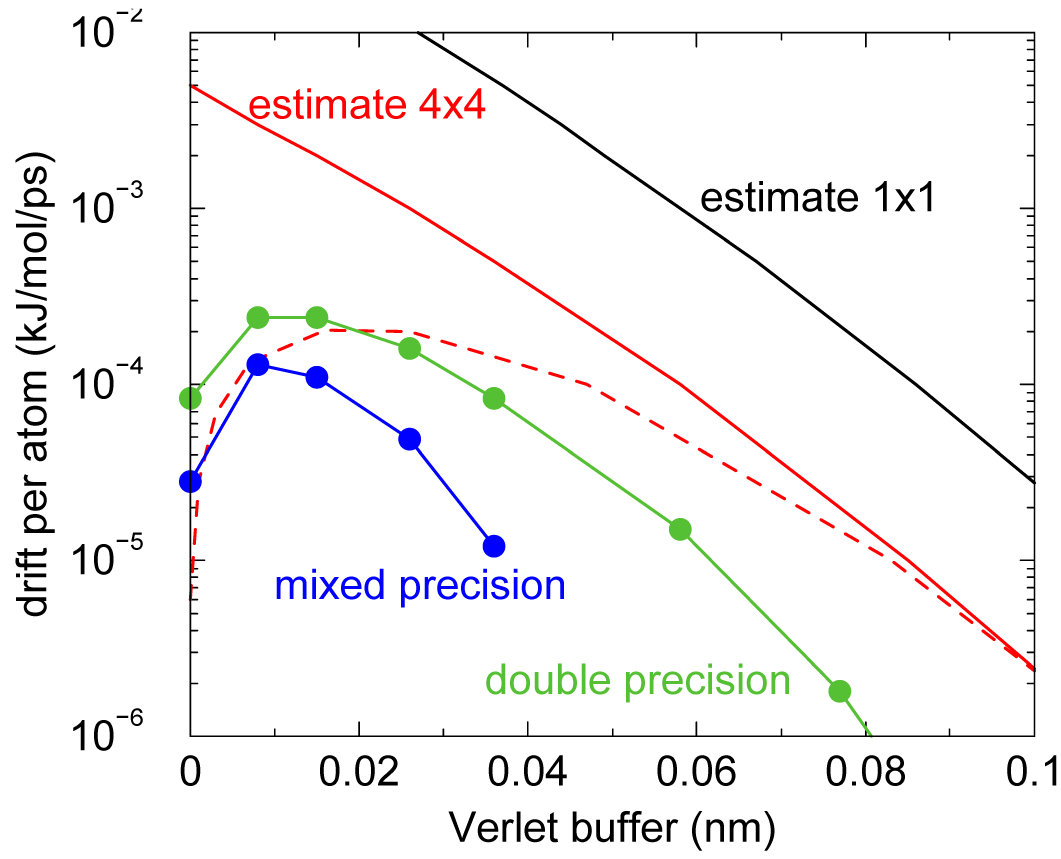
ewald-rtol设置为 \(10^{-5}\); 该参数影响截断处的势能形状. 图中显示了因有限Verlet缓冲大小, 对 \(1\times1\) 和 \(4\times4\) 原子对列表, 不使用和使用(虚线)正负误差抵消时引起的误差估计. 图中显示的实际能源漂移在模拟时使用了双精度和混合精度. 使用单精度时, 由SETTLE约束算法的舍入误差引起的漂移在缓冲尺寸很大时变为负值. 注意, 缓冲大小为零时, 实际漂移很小, 因为正的(H-H)和负的(O-H)能量误差会相互抵消.截断假象与切换相互作用
使用Verlet方案时, 可以平移对势使其在截断处为零, 以保证势能等于力的积分. 在组方案中, 只有当势能满足在截断距离处的值为零时, 才可以保证势能等于力的积分. 然而, 当力在截断处不为零时仍会引起能量漂移. 这种影响非常小, 通常觉察不到, 因为其它积分误差(如来自约束的)可能占主到地位. 为完全避免截断假象, 可以将非键力在到达近邻列表截断前精确地切换至零(在GROMACS中有几种方式完成, 见4.1.5节). 这样就形成一个大小等于近邻列表截断, 小于最长相互作用截断的缓冲.
使用组截断方案, 也可以选择让mdrun只在需要时才更新近邻列表, 也就是当一个或多个粒子从它们所属的电荷组(见3.4.2节)的几何中心移动的距离超过半个缓冲大小时, 中心由前一步的近邻搜索决定. 此选项可保证没有截断假象, 注意, 对较大的体系, 这种计算的代价很高, 因为近邻列表更新频率将由移动稍微超过半个缓冲长度的一两个粒子决定(这甚至都不意味着近邻列表无效), 而99.99%的粒子近邻列表依然有效.
简单搜索
由于方程3.1和3.6, 连接处于截断距离 \(R_c\) 内的映象的向量 \(\bi r_{ij}\) 可通过下面方法获得:
\[\alg \bi r''' &= \bi r_j-\bi r_i \tag{3.13} \\ \bi r'' &= \bi r'''-\bi c * \text{round}(r_z'''/c_z) \tag{3.14} \\ \bi r' &= \bi r''-\bi b * \text{round}(r_y''/b_y) \tag{3.15} \\ \bi r_{ij} &= \bi r'-\bi a * \text{round}(r_x'/a_x) \tag{3.16} \\ \ealg\]
当需要计算三斜盒子中两粒子间的距离时, 它们不服从方程3.1, 需要将许多盒向量的组合进行移位, 以找到最近的映象.
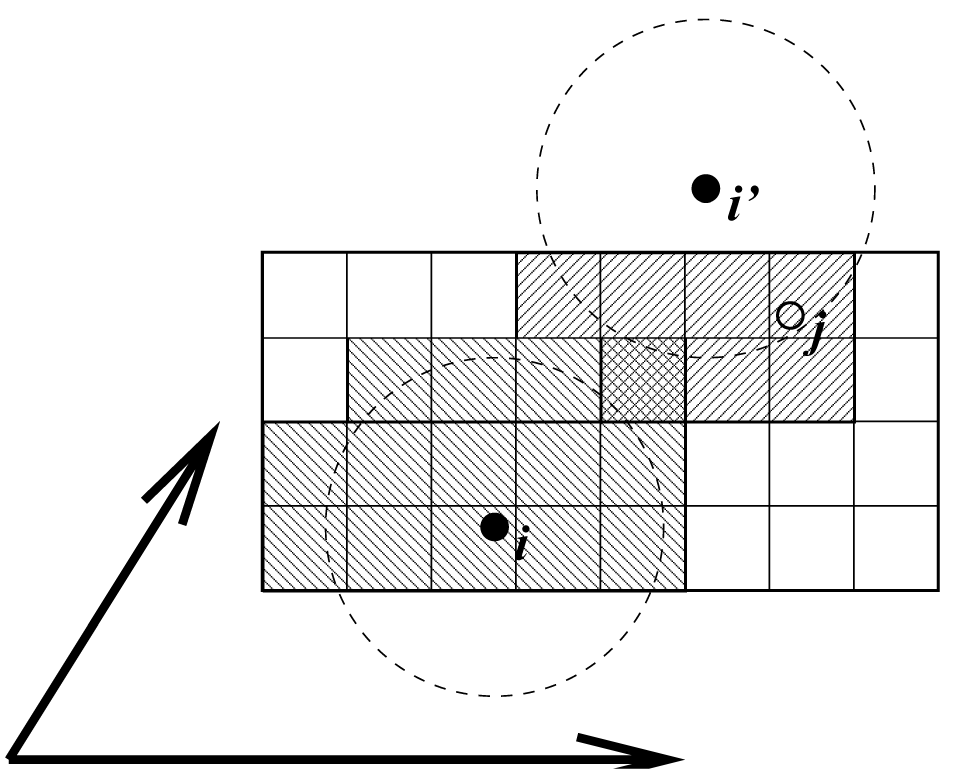
格点搜索
格点搜索示意图见图3.6. 所有粒子被置于NS格点上, 每一方向上的最小间距 \(\ge R_c/2\). 在每一盒向量方向上, 粒子 \(i\) 有三个映象. 对每一方向映象可能是–1, 0或1, 相应于平移–1, 0或+1个盒向量. 对 \(i\) 的近邻, 我们不是先搜索周围的NS格点单元再计算映象, 而是先构造映象再搜索对应 \(i\) 的映象的近邻. 如图3.6所示, 对 \(i\) 的不同映象, 一些格点单元的搜索次数会查过一. 这并不是一个问题, 因为由于最小映象约定, 最多只有一个映象能够“看到”粒子 \(j\). 对每个粒子, 搜索的近邻单元少于125(53)个. 因此, 算法对粒子数是线性标度的. 虽然前因子很大, 当粒子数超过几百时, 标度行为使得算法远优于标准的 \(O(N^2)\) 算法. 格点搜索对长方盒子与三斜盒子同样快. 这样对大多数蛋白质和多肽模拟, 使用菱形十二面体盒子更好.
电荷组
最初引入电荷组是为了减少库仑相互作用的截断假象. 使用普通截断时, 当带(部分)电荷的原子移进移出截断半径时, 势能与力会出现明显的跃变. 当所有化学基团的净电荷为零时, 通过移动净电荷为零的原子组进出近邻列表可以减小这些跃变. 这些原子组被称为电荷组. 这种方法将截断效应从电荷电荷水平降低到衰减快得多的偶极偶极水平. 随着全范围静电方法的出现, 如粒子网格Ewald方法(见4.8.2节), 不再需要使用电荷组来提高精度了. 依赖于如何创建近邻列表, 如何计算相互作用, 电荷组甚至可能对精度和效率有小的负面影响.
但仍然有一个重要原因来使用“电荷组”: 组截断方案的效率. 当适用时, 近邻搜索基于在分子拓扑中定义的电荷组进行. 若两个电荷组原子的 几何中心 之间的最近映象距离小于截断半径, 对列表中会包含电荷组之间的所有原子对. 例如, 对水体系的近邻搜索, 当每个分子被视为一个电荷组时 会快32=9倍. 另外, 计算水中原子受力的高度优化的循环只能用于水分子中的所有原子形成单个电荷组的情况. 目前使用 近邻搜索组 可能更合适, 但由于历史原因仍保留了名称电荷组. 当发展新的力场时, 建议使用3到4个原子的电荷组以获得最佳性能. 对全原子力场这相对容易, 因为可以简单地把氢原子, 一些情况下的氧原子, 置于与其相连的重原子相同的电荷组中, 如CH3, CH2, CH, NH2, NH, OH, CO2, CO.
使用Verlet截断方案时, 电荷组被忽略.
3.4.3 计算力
势能
当计算力时, 同时会计算每项相互作用的势能. 总势能是所有项的加和, 如Lennard-Jones项, 库仑项和键合项. 也可以计算 能量监测组 对这些项的贡献, 组成能量监测组的原子可以单独定义(参见3.3节).
动能和温度
对含有 \(N\) 个粒子的体系, 温度由总动能给出:
\[E_{\text{kin} }={1\over2} \sum_{i=1}^N m_i v_i^2 \tag{3.17}\]
由此可计算绝对温度 \(T\):
\[{1\over2}N_{\text{df} }kT=E_{\text{kin} } \tag{3.18}\]
其中 \(k\) 为玻尔兹曼常数, \(N_{\text{df} }\) 为自由度数, 可根据下式计算:
\[N_{\text{df} } = 3N-N_c-N_{\text{com} } \tag{3.19}\]
这里 \(N_c\) 为施加在体系上的 约束 的数目. 在进行分子动力学模拟时, 必须去除 \(N_{\text{com} }=3\) 个额外的自由度, 因为三个质心速度是运动常量, 通常设置为零. 当在真空中进行模拟时, 绕质心的转动也可以被去除, 这种情况下 \(N_{\text{com} }=6\). 当使用一个以上的温度耦合组时, 第 \(i\) 组的自由度数目为:
\[N_{\text{df} }^i=(3N^i-N_c^i) {3N-N_c-N_{\text{com} } \over 3N-N_c} \tag{3.20}\]
当计算三斜体系的压力, 或者体系受到剪切力作用时, 将动能写成张量形式能带来方便
\[\bi E_{\text{kin} }={1\over2}\sum_i^N m_i \bi v_i \otimes \bi v_i \tag{3.21}\]
压力和维里
压力张量 \(\bi P\) 可以通过动能 \(E_{\text{kin} }\) 和维里 \(\bi \X\) 的差值来计算:
$$ \bi P={2\over V}(\bi E_{\text{kin}}-\bi \X) \tag{3.22}$$
其中 \(V\) 为盒子的体积. 在各向同性体系中被用于压力耦合的标量压力 \(P\) 为:
\[P = \text{trace} (\bi P)/3 \tag{3.23}\]
维里张量 \(\bi \X\) 定义为:
\[\bi \X = -{1\over2} \Sum_{i < j} \bi r_{ij} \otimes \bi F_{ij} \tag{3.24}\]
GROMACS计算维里的实现方法请参考B.1节.
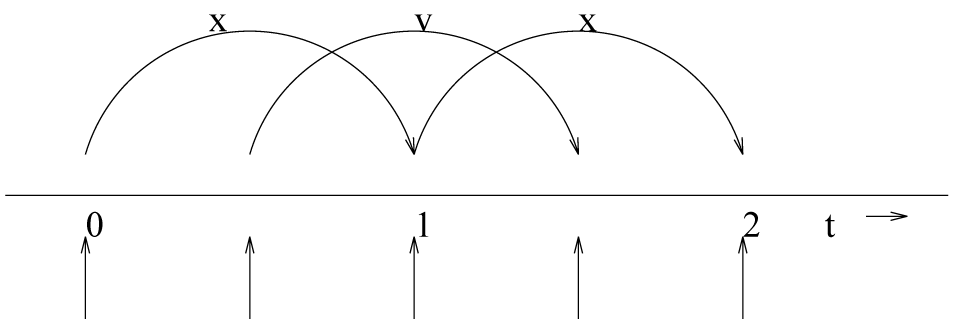
3.4.4 蛙跳式积分方法
GROMACS中默认的MD积分方法是所谓的 蛙跳式算法 [20], 用于积分运动方程. 当需要非常精确的积分方法并采用温度和/或压力耦合时, 使用速度Verlet积分方法可能更好(参见3.4.5节). 蛙跳式算法使用了 \(t\) 时刻的位置 \(\bi r\) 和 \(t-{1\over2}\D t\) 时刻的速度 \(\bi v\), 根据 \(t\) 时刻的位置计算出力 \(\bi F(t)\), 并利用下面的方法更新位置和速度
\(\alg \bi v(t+{1\over2}\D t) &= \bi v(t-{1\over2}\D t)+{\D t\over m}\bi F(t) \tag{3.25} \\ \bi r(t+\D t) &= \bi r(t)+\D t \bi v(t+{1\over2}\D t) \tag{3.26} \ealg\)
图3.7是蛙跳式算法的形象说明. 它产生的轨迹与Verlet算法[21]完全一样, 它更新位置的方法是
\[\bi r(t +\D t)=2 \bi r(t)-\bi r(t-\D t) +{1\over m} \bi F(t)\D t^2 + O(\D t^4) \tag{3.27}\]
蛙跳式算法对 \(\bi r\) 具有三阶精度, 并且时间可逆. 关于此算法的优点以及与其他时间积分算法的比较, 请参看文献[22].
为考虑温度耦合和压力耦合并扩展以包含约束守恒, 我们修改了运动方程, 详细情况将在后面进行讨论.
3.4.5 速度verlet积分方法
GROMACS也实现了速度Verlet算法[23], 尽管它与所有选项的整合还没有完全好. 在速度Verlet方法中, 利用 \(t\) 时刻的位置 \(\bi r\) 和速度 \(\bi v\) 积分运动方程, 并不需要前半步时刻的速度.
\(\alg \bi v(t+{1\over2}\D t) &= \bi v(t)+{\D t \over 2m} \bi F(t) \tag{3.28} \\ \bi r(t+\D t) &= \bi r(t)+\D t \bi v(t+{1\over2}\D t) \tag{3.29} \\ \bi v(t+\D t) &= \bi v(t+{1\over2}\D t)+{\D t \over 2m} \bi F(t+\D t) \tag{3.30} \ealg\)
或者, 等价地,
\(\alg \bi r(t+\D t) &= \bi r(t)+\D t \bi v + {\D t^2 \over 2m} \bi F(t) \tag{3.31} \\ \bi v(t+\D t) &= \bi v(t)+{\D t \over 2m}[\bi F(t)+ \bi F(t+\D t)] \tag{3.32} \ealg\)
不使用温度或压力耦合, 并从 对应 的起始点出发, 蛙跳式方法和速度Verlet方法会给出完全相同的轨迹, 你可以容易地利用上面给出的方程证明这一点. 给定一个具有 相同 起始点 \(\bi x(0)\) 和 \(\bi v(0)\) 的起始文件, 蛙跳式方法和速度Verlet方法 不会 给出相同的轨迹, 因为蛙跳式方法的速度对应于 \(t=-{1\over2}\D t\) 时刻, 而速度Verlet方法会认为它们对应于 \(t=0\) 时刻.
3.4.6 理解可逆的积分方法: Trotter分解
为进一步理解速度Verlet和蛙跳式积分方法之间的关系, 我们引入动力学中的可逆Trotter公式, 它对于理解GROMACS的热浴和压力浴的实现也是非常有用的.
对一个耦合一阶微分方程系统, 可利用演化算符用得到体系从 \(t=0\) 时刻到 \(t\) 时刻的演化
\(\alg \G(t) &= \exp(iLt) \G(0) \\ iL &= \dot \G \cdot \nabla_\G \tag{3.33} \ealg\)
其中 \(L\) 为Liouville算符, \(\G\) 为自变量(位置和速度)的多维向量. 将精确算符的一个短时间近似, 在 \(\D t=t/P\) 时刻是精确的, 连续应用 \(P\) 次可使体系演化为
\[\G(t)=\prod_{i=1}^P \exp(iL\D t) \G(0) \tag{3.34}\]
对NVE动力学, Liouville算子为
\[iL=\Sum_{i=1}^N \bi v_i \cdot \nabla_{\bi r_i} + \Sum_{i=1}^N {1 \over m_i} \bi F(r_i) \cdot \nabla_{\bi v_i} \tag{3.35}\]
它可以被分解为两个算符的加和
\(\alg iL_1 &= \Sum_{i=1}^N {1 \over m_i} \bi F(r_i) \cdot \nabla_{\bi v_i} \\ iL_2 &= \Sum_{i=1}^N \bi v_i \cdot \nabla_{\bi r_i} \tag{3.36} \ealg\)
这样, 真正动力学在短时间内, 对称可逆的近似为
\[\exp(iL\D t) = \exp(iL_2{1\over2}\D t) \exp(iL_1 \D t) \exp(iL_2{1\over2}\D t)+O(\D t^3) \tag{3.37}\]
这对应于速度Verlet积分方法. 第一个 \({1\over2}\D t\) 指数项对应于半个速度步, 第二个 \(\D t\) 指数项对应于一个完整的速度步, 最后的 \({1\over2}\D t\) 指数项是最终的半个速度步. 对于未来时刻 \(t=n\D t\), 上式变为
\(\alg \exp(iLn\D t) &\approx &\left( \exp(iL_2{1\over2}\D t) \exp(iL_1 \D t) \exp(iL_2{1\over2}\D t) \right)^n \\ & \approx &\exp(iL_2{1\over2}\D t) \left( \exp(iL_1 \D t) \exp(iL_2 \D t) \right)^{n-1} \\ & &\exp(iL_1 \D t) \exp(iL_2{1\over2}\D t) \tag{3.38} \ealg\)
利用这种形式, 我们可以很容易看到的不同Verlet积分方法之间的差异. 蛙跳式积分方法可以看作使用方程3.37的 \(\exp(iL_1 \D t)\) 项代替半步速度项启动, 得到
\[\exp(iL n \D t) = \exp(iL_1 \D t) \exp(iL_2 \D t) +O(\D t^3) \tag{3.39}\]
这里, 速度的整步处于 \(t-{1\over2}\D t\) 和 \(t+{1\over2}\D t\) 之间, 因为它是速度Verlet中速度半步的组合. 对未来的时刻 \(t=n\D t\), 此式变为
\[\exp(iL n \D t) \approx \left( \exp(iL_1 \D t) \exp(iL_2 \D t) \right)^n \tag{3.40}\]
虽然上式初看起来不对称, 只要整个速度步处于 \(t-{1\over2}\D t\) 和 \(t+{1\over2}\D t\) 之间, 这就是在循环中的不同地方启动速度Verlet的一种简单方法.
尽管蛙跳式方法和速度Verlet方法得到的轨迹和势能完全相同, 动能和温度并不一定相同. 标准的速度Verlet方法使用 \(t\) 时刻的速度计算动能, 因而只有 \(t\) 时刻的温度, 动能是对所有粒子的加和
\(\alg KE_{\text{full} }(t) &= \Sum_i \left({1\over 2m_i}\bi v_i(t) \right)^2 \\ &=\Sum_i {1\over 2m_i} \left({1\over 2}\bi v_i(t-{1\over2}\D t) + {1\over 2}\bi v_i(t+{1\over2}\D t) \right)^2 \tag{3.41} \ealg\)
平方出现于平均的 外部. 标准的蛙跳式方法基于时间步 \(t+{1\over2}\D t\) 和 \(t-{1\over2}\D t\) 的平均动能来计算 \(t\) 时刻的动能, 或对所有粒子的加和
\[KE_{\text{average} }(t) =\Sum_i {1\over 2m_i} \left({1\over 2}\bi v_i(t-{1\over2}\D t)^2 + {1\over 2}\bi v_i(t+{1\over2}\D t)^2 \right) \tag{3.42}\]
其中平方处于平均的 内部.
速度Verlet方法的非标准形式会对动能 \(KE(t+{1\over2}\D t)\) 和 \(KE(t-{1\over2}\D t)\) 进行平均, 与蛙跳式方法相同. GROMACS现在也实现了这种方法(利用.mdp文件中的md-vv-avek选项). 无温度耦合和压力耦合时, 半步动能平均的速度Verlet方法和蛙跳式方法在数值精度内是完全相同的. 但是, 对于控温和控压方案, 半步动能平均的速度Verlet方法和蛙跳式方法会有所不同, 我们将在控温器和控压器部分对此进行讨论.
对于给定的步长, 半步平均的动能和温度稍微准确一些; 比起整步动能(使用md-vv), 采用半步平均的动能(md和md-vv-avek)得到的平均动能的差异更接近于小步长极限情况下获得的动能. 对NVE模拟, 这种差别通常不明显, 因为粒子的位置与速度仍然完全相同; 差别在于模拟温度含义的 解释, 而 不 在于所产生的轨迹. 虽然半步平均方法得到的动能更精确, 意味着当时间步长变大时它受的影响小些, 但这种方法的噪声更大. 与整步动能方法相比, 半步平均动能方法得到的体系总能量(动能和势能的总和)的RMS偏差更大(在大多数情况下约高一倍). 漂移仍然是相同的, 并且轨迹也完全相同.
对NVT模拟, 两种方法 将 会有差异, 正如控温部分所讨论的, 因为会调节粒子的速度以使得模拟的动能, 以任何一种方式计算,都能达到与设定温度相应的分布. 在这种情况下, 三种方法不会给出完全相同的结果.
由于速度和位置都定义于同一时刻 \(t\), 速度Verlet积分方法可用于一些方法中, 特别是那些严格正确的控压方法, 实际上这些控压方法不能使用蛙跳式积分方法. 相比蛙跳式积分方法, 速度Verlet方法多耗费的时间可以忽略不计, 但目前需要的通讯调用多一倍. 在大多数情况下, 尤其是对于大的体系,其通讯速度对并行化非常重要, 热力学系综之间的差异以 \(1/N\) 极限消失. 当只需要NVT系综时, 蛙跳式可能是首选的积分方法. 对控压模拟, 热力学细节非常重要, 只有速度Verlet方法能给出真正的系综. 在任一情况下, 都可能需要采用双精度进行模拟以得到正确的热力学校正细节.
3.4.7 双程截断
为了节省计算时间, 相比变化迅速的力, 对变化缓慢的力计算时所用的频率可以低些. 在GROMACS中, 可以对短程和长程非键相互作用采用这样的多重时间步长分解. 直到GROMACS 4.0版本, 对此都采用了一种不可逆的积分方案, 这种方案也被用于GROMOS模拟包: 每 \(n\) 步计算一次长程力, 随后将这些值(不加修改)用于方程3.25中的后面 \(n-1\) 积分步. 这种不可逆的方案能量守恒性不好, 取样可能不充分. 从4.5版本开始, 采用了可逆Trotter分解方案的蛙跳式方法[24]. 在这种积分方法中, 每 \(n\) 步计算一次长程力, 然后使用时间步长 \(\D t_{LR}=n\D t\) 将其应用到方程3.25中的速度,
\[\bi v(t+{1\over2}\D t)=\begin{cases} \bi v(t-{1\over2}\D t)+{1\over m}[\bi F_\text{SR}(t)+n\bi F_\text{LR}(t)\D t]&, &\; \text{step} \% n=0 \\ \bi v(t-{1\over2}\D t)+{1\over m}\bi F_\text{SR}(t)\D t &, &\; \text{step} \% n \ne 0 \\ \end{cases} \tag{3.43}\]
参数 \(n\) 等于近邻列表的更新频率. 在4.5版本中, 多重时间步的速度Verlet方案进尚未完全实现.
一些其他的模拟程序对键合力和/或PME网格力使用多重时间步长方法. 在GROMACS中, 我们(还)没有实现这个方法, 因为我们有着不同的想法. 键可以被约束(这也是对物理量子振子的更佳近似), 这允许将最小时间步长增加至更大值. 这不仅将计算力的次数减半, 也将更新计算的次数减半. 对于更大的时间步长, 涉及氢原子的键角振动可以使用虚拟相互作用位点移除(见6.8节), 这使得最短时间步达到多时间步方案中PME网格的更新频率.
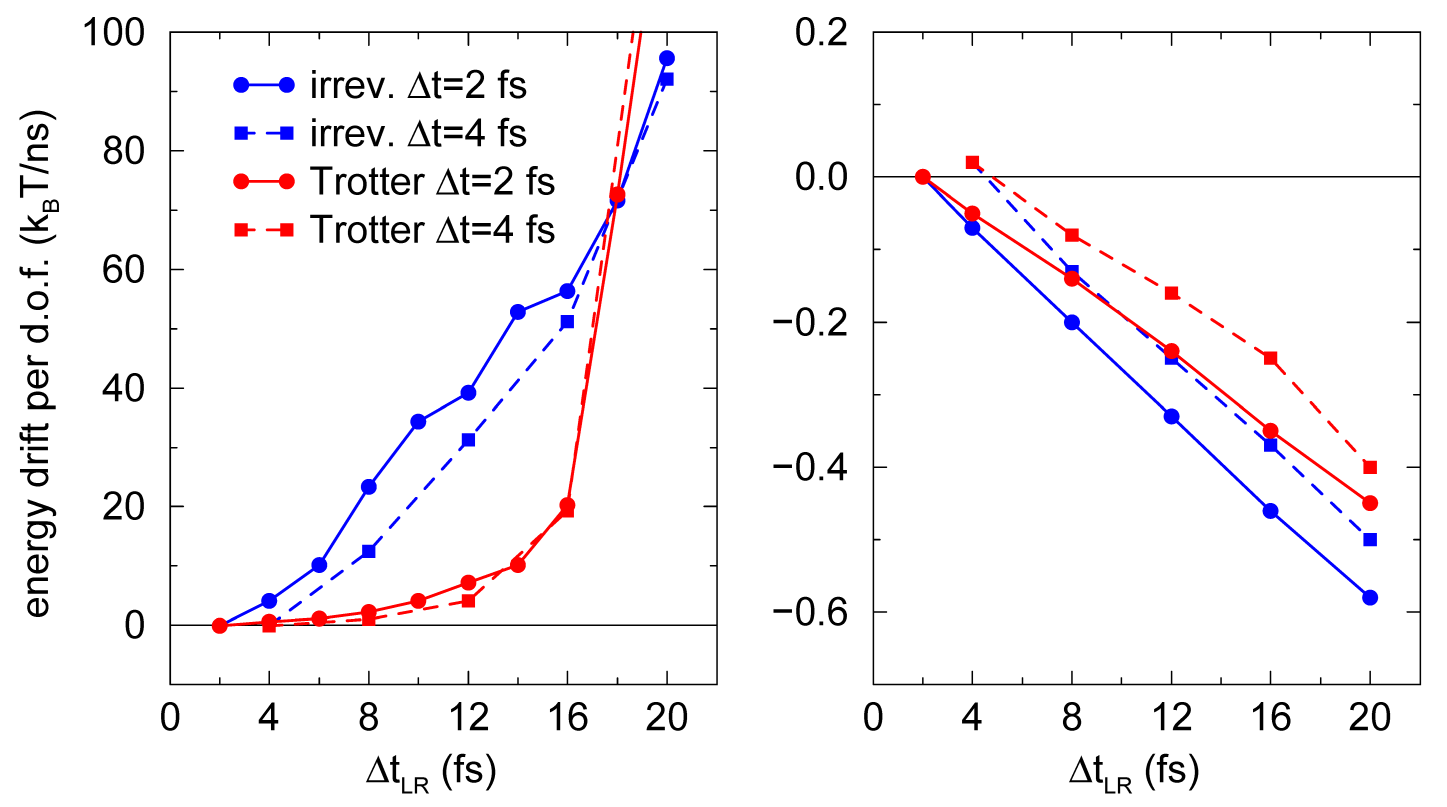
作为一个例子, 我们在如3.8中展示了积分300 K温度下SPC/E水体系运动方程的能量守恒性. 为避免截断效应, 使用了反应场, \(\e_{RF}=\infty\) 和移位Lennard-Jones相互作用. 二者都使用了缓冲. 长程相互作用在1.0和1.4 nm之间进行计算. 从图3.7可以看到, 对静电相互作用, 直到 \(\D t_{LR}=16\) fs, Trotter方案的能量守恒性都要好一个数量级. 静电相互作用强烈地依赖于水分子变化很快的取向. 对Lennard-Jones相互作用, 能量漂移与 \(\D t_{LR}\) 呈线性关系, 大致比静电小两个数量级. Lennard-Jones力比库仑力小, 它们主要受水分子的平动影响, 而不是转动.
3.4.8 温度耦合
直接使用的分子动力学模拟对应于NVE系综(粒子数不变, 体积不变, 能量恒定的系综), 我们希望计算的大多数物理量实际上对应于等温(NVT)系综, 也被称为正则系综. GROMACS可以使用Berendsen的 弱耦合 方案[25], 通过Andersen恒温器的随机化[26], 扩展系综的Nose-Hoover方案[27, 28], 或速度重缩放方案[29]来模拟恒温过程, 这些方案各自的优缺点将在下面介绍.
还有其他一些原因使得我们需要对体系的温度进行调控(平衡过程中的漂移, 力截断和积分误差引起的漂移, 外力或摩擦力导致的加热), 但从热力学的观点来看, 这并不是完全正确的. 在某些情况下, 这些做法只是掩盖了问题(增加了体系的温度), 而没有从根本上解决问题(动力学与真实物理过程之间存在的偏差). 对于大的体系, 系综平均引起的误差, 用于消除温度缓慢漂移的控温对结构性质的影响几乎可以忽略. 但如果没有进行完全的综合比较, 在解释模拟结果时必须谨慎.
Berendsen温度耦合
Berendsen算法模仿了与给定温度 \(T_0\) 的外部热浴相连, 并具有一级动力学特征的弱耦合. 参考文献[30]将它与Nose-Hoover方案进行了比较. 该算法的效果是, 根据下式慢慢校正体系温度对 \(T_0\) 的偏差:
\[{dT \over dt} = {T_0-T \over \t} \tag{3.44}\]
这意味着温度偏差指数衰减, 其时间常数为 \(\t\). 这种耦合方法的优点是, 耦合的强度可以改变以适应用户的需要: 对于以平衡为目的模拟可采取很小的时间常数(如0.01 ps); 但对于可靠的平衡模拟, 可采用更大的时间常数(如0.5 ps), 在这种情况下, 它几乎不会影响动力学的守恒性.
Berendsen恒温可降低动能的涨落. 这意味着, 它不会产生正确的正则系综, 所以严格来说, 采样是不正确的. 引入误差的标度为 \(1/N\), 因此对于非常大的体系, 大部分系综平均值不会受到显著影响, 除了动能本身的分布. 然而, 涨落性质, 如热容量, 将受到影响. 后面将要描述的速度重缩放恒温器[29]是一种与此类似的控温方法, 但能产生正确的系综.
流入或流出体系的热量受到对每个粒子的速度进行重新缩放的影响, 缩放每步或每 \(n_{\text{tc}}\) 步进行一次, 使用一个与时间相关的因子 \(\l\), :
\[\l=\left[ 1+{n_{\text{TC}} \D t \over \t_T} \left\{ {T_0 \over T(t-{1\over2}\D t)}-1\right\} \right] \tag{3.45}\]
参数 \(\t_T\) 接近但不完全等于温度耦合的时间常数 \(\t\) (方程3.44):
\[\t=2C_V \t_T / N_{df} k \tag{.46}\]
其中 \(C_V\) 为体系总的热容, \(k\) 为玻尔兹曼常数, \(N_{df}\) 为总的自由度数. \(\t \ne \t_T\) 的原因在于, 缩放速度引起的动能变化会部分地在动能和势能之间进行重新分布, 因此, 温度的变化小于缩放能量. 实际上, 比值 \(\t/\t_T\) 的范围从1(气体)到2(简谐固体)到3(水). 当我们使用术语“温度耦合时间常数”时, 我们指的是参数 \(\t\). 注意 缩放因子 \(\l\) 在实际中被限制在 \(0.8<=\l<=1.25\) 的范围内, 以避免当其过大时导致模拟体系崩溃. 在正常使用中, \(\l\) 总是会更接近1.0.
速度重缩放温度耦合
速度重缩放恒温器[29]本质上是一个Berendsen恒温器(见上文), 并附加了一个随机项, 以保证能够给出正确的动能分布, 使用时根据下面的公式对动能进行修改:
\[dK = (K_O-K){dt \over \t_T}+2 \sqrt{ {K K_0 \over Nf} } {dW \over \sqrt \t_T} \tag{3.47}\]
其中 \(K\) 为动能, \(N_f\) 为自由度数, \(dW\) 为Wiener过程. 除了随机数种子外, 没有另外的参数. 这种温控器能够产生正确的正则系综, 仍然具有Berendsen温控器的优点: 温度偏差一阶衰减, 无振荡. 当使用 \(NVT\) 系综时, 守恒的能量会被写入到能量文件和log文件.
Andersen温控器
保持恒温系综的一种简单的方式如下, 使用 \(NVE\) 积分方法, 并周期性地从麦克斯韦-玻尔兹曼分布中重新选择粒子的速度. [26] 这可以通过每 \(\t_T/\D t\) 步同时(大规模碰撞)将所有粒子的速度进行随机化(andersen-massive), 或通过每步以小概率, 等于 \(\D t/\t\), 随机化每个粒子(andersen), 在这两种情况下, \(\D t\) 为时间步长, \(\t_T\) 为特征的耦合时间尺度. 由于约束的操作方式, 同一约束组中所有粒子的速度必须同时随机化. 由于并行问题, andersen选项目前(5.0)还不能用于含有约束的体系. andersen-massive的使用不受约束限制. 此温控器也是目前唯一可与速度Verlet算法一同使用的, 因为它在每个时间步的直接对速度进行操作.
这个算法完全避免了其他恒温算法具有的一些遍历性问题, 像能量不能在体系的能量去耦合组分间来回流动, 如在速度缩放运动中. 但是, 它可以通过随机化体系的相关运动降低体系的动能, 包括减慢采样, 当 \(\t_T\) 处于中等水平时(小于10 ps). 因此, 该算法通常不能用于考察体系的动力学或输运性质. [31]
Nose-Hoover温度耦合
Berendsen弱耦合算法可以非常高效地将体系弛豫到到目标温度, 但是, 一旦系统达到平衡, 维持正确的正则系综更重要. 很可惜, 弱耦合方案并不能满足这一点.
为了使用正则系综模拟, GROMACS还支持扩展系综方法. 这种方法首先由Nose提出[27], 后经Hoover修改[28]. 通过在运动方程中引入一个热容器和一个摩擦项, 方法对体系的哈密顿量进行了扩展. 摩擦力正比于每个粒子的速度和摩擦参数 \(\x\) 的乘积. 这个摩擦参数(或“热浴”变量)是一个完全的动力学量, 有着自己是动量(\(p_\x\))和运动方程; 其时间导数由当前动能和参考温度之间的差值来计算.
在这个公式中, 图3.3中粒子的运动方程被替换为:
\[{d^2 \bi r_i \over dt^2}={\bi F_i \over m_i}-{p_\x \over Q}{d \bi r_i \over dt} \tag{3.48}\]
其中热浴参数 \(\x\) 的运动方程为:
\[{d p_\x \over dt}=(T_0-T) \tag{3.49}\]
参考温度以 \(T_0\) 表示, 而 \(T\) 为体系当前的瞬时温度. 耦合强度由常数 \(Q\) (通常被称为容器的“质量参数”)和参考温度共同决定[1]
Nose-Hoover运动方程的守恒量并不是总能量, 而是
\[H=\Sum_{i=1}^N {\bi p_i \over 2m_i}+U(\bi r_1, \bi r_2,...,\bi r_N)+{p_\x^2 \over 2Q}+N_f kT\x \tag{3.50}\]
其中 \(Nf\) 为总的自由度数.
依我们看, 利用质量参数来描述耦合强度让人有点难以理解, 特别是它还依赖于参考温度(在一些实现中 \(Q\) 的定义还和体系的自由度数有关). 为了维持耦合强度, \(Q\) 的改变必须正比于参考温度的改变. 基于这个原因, 我们更愿意让GROMACS用户使用体系和容器之间动能的振荡周期 \(\t_T\) 来代替 \(Q\), 它通过下式直接与 \(Q\) 和 \(T_0\) 相关:
\[Q={\t_T^2 T_0 \over 4 \p^2} \tag{3.51}\]
这为选择Nose-Hoover耦合强度(弱耦合弛豫与此类似)提供了一个更为直观的方式, 并且 \(\t_T\) 与体系的大小和参考温度无关.
然而, 要特别注意弱耦合方案和Nose-Hoover算法的区别: 使用弱耦合你将得到一个具有强烈阻尼的 指数弛豫, 而Nose-Hoover方法产生 振荡弛豫. Nose-Hoover耦合需要的实际弛豫时间 比你选择的振荡周期要大几倍. 这些振荡(相比于指数弛豫)也意味着时间常数通常应该比弱耦合所使用的弛豫时间大4–5倍, 但你可以根据情况改变.
Nose-Hoover动力学在简单的体系, 如谐振子集合中, 可能是非遍历的, 这意味着即使模拟运行了无限长时间, 也只能对相空间的一小部分进行采样. 因此, 人们发展了Nose-Hoover链方法, 其中每个的Nose-Hoover控温器都有自己的Nose-Hoover恒温器来控制其温度. 当恒温器链的长度趋向无限时, 可以保证过程是遍历的. 只使用几个链可以大大提高遍历性, 但最近的研究表明, 体系仍然是非遍历的, 并且仍然不完全清楚其实际影响[32]. 目前, 链的默认数目为10, 但用户可以更改. 在使用Nose-Hoover链的情况下, 方程修改为下面的形式以包含恒温粒子链[33]:
\(\alg {d^2 \bi r_i \over d t^2} &= {\bi F_i \over m_i}-{p_{\x_1} \over Q_1}{d\bi r_i \over dt} \\ {d p_{\x_1} \over d t} &= (T-T_0)-p_{\x_1}{p_{\x_2} \over \x_2} \\ {d p_{\x_{i=2...N} } \over d t} &= \left( {p_{\x_{i-1} }^2 \over Q_{i-1}} -kT \right) -p_{\x_i} {p_{\x_{i+1}} \over Q_{i+1}} \\ {d p_{\x_N} \over d t} &= \left( {p_{\x_{N-1} }^2 \over Q_{N-1}} -kT \right) \ealg \tag{3.52}\)
Nose-Hoover链的守恒量为
\[H=\Sum_{i=1}^N {\bi p_i \over 2m_i}+U(\bi r_1, \bi r_2, ...,\bi r_N)+\Sum_{k=1}^M {p_{\x_k}^2 \over 2Q_k'}+ N_f kT \x_1 + kT \Sum_{k=2}^M \x_k \tag{3.53}\]
Nose-Hoover恒温器变量的值与速度一般不包含在输出中, 因为它们会占用相当大的空间并且通常对于分析模拟结果不是很重要. 但是, 可以通过定义环境变量GMX_NOSEHOOVER_CHAINS, 将链中所有Nose-Hoover粒子的位置和速度输出到.edr文件中. 在目前的版本中, 蛙跳式积分方法只能使用长度为1的Nose-Hoover链, 但在以后的版本中可能会支持更长的链.
如在积分方法那节讲的, 对于温度耦合, 速度Verlet方法和蛙跳式算法在试图匹配参考温度时, 对温度的计算有所不同. 速度Verlet(md-vv)使用了整步动能, 而蛙跳式缩放和md-vv-avek使用了半步平均的动能.
通过再次考查Trotter分解, 我们可以更好地理解这些等温积分方法之间的差异. 对Nose-Hoover动力学(为简单起见, 使用的链长 \(N=1\), 更多细节请参考文献[34]), 将Liouville算子劈分为
\[iL=iL_1+iL_2+iL_{\text{NHC} } \tag{3.54}\]
其中,
\(\alg iL_1 &=\Sum_{i=1}^N \left[{\bi p_i \over m_i}\right] \cdot {\partial \over \partial \bi r_i} \\ iL_2 &=\Sum_{i=1}^N {\bi F_i \cdot {\partial \over \partial \bi p_i} } \\ iL_{\text{NHC} } &= \Sum_{i=1}^N -{p_\x \over Q} \bi v_i \cdot \nabla \bi v_i + {p_\x \over Q} {\partial \over \partial \x} + (T-T_0) {\partial \over \partial p_\x} \ealg \tag{3.55}\)
对于使用Nose-Hoover温度控制的标准速度Verlet方法, 上式变为
\(\alg \exp(iL\D t)=\; &\exp(iL_{\text{NHC} }\D t/2) \exp(iL_2 \D t/2) \\ &\exp(iL_1 \D t) \exp(iL_2 \D t/2) \exp(iL_{\text{NHC} }\D t/2) + O(\D t^3) \ealg \tag{3.56}\)
对于使用md-vv-avek的半步平均温度控制, 这种分解不适用, 因为我们在第二速度步完成前不可能得到整步的温度. 然而, 我们可以通过交换分解中NHC和速度部分的位置构造另一个分解, 它仍然是可逆的,
\(\alg \exp(iL\D t)=\; &\exp(iL_2 \D t/2) \exp(iL_{\text{NHC} }\D t/2) \exp(iL_1 \D t) \\ &\exp(iL_{\text{NHC} }\D t/2) \exp(iL_2 \D t/2) + O(\D t^3) \ealg \tag{3.57}\)
利用这种形式我们可以很容易地看出各种速度Verlet积分方法之间的差异. 蛙跳式积分方法可视为以方程3.57 $$\exp(iL_1\D t)$ 之前的项开始, 得到:
\(\alg \exp(iL\D t)=\; & \exp(iL_1 \D t) \exp(iL_{\text{NHC} }\D t/2) \\ &\exp(iL_2 \D t) \exp(iL_{\text{NHC} }\D t/2) + O(\D t^3) \ealg \tag{3.58}\)
然后使用了一些代数技巧来求解, 因为有一些量在实际计算之前就需要知道[35].
组内温度耦合
在GROMACS中, 温度耦合可用于原子组, 通常是蛋白质和溶剂. 引入这种算法的原因是, 由于各种不同的效应, 包括截断等等, 不同组分之间的能量交换并不完美. 如果现在整个体系耦合到一个热浴, 水(受到的截断噪声最大)将倾向于升温, 而蛋白质会冷却. 这通常会导致二者之间有100 K的温度差异. 通过使用合适的静电方法(PME), 这些差异会小很多, 但仍然不可忽视. 组内温度耦合的参数中在mdp文件中给出. 最近的研究表明, 蛋白质和水之间细微的温度差异, 实际上可能是虚假的, 是由时间步长有限时计算温度的方式导致的, 非常大的温度差异很可能是体系严重出错的标志, 应该仔细检查[36].
应该提到一种特殊情况: 可以只对体系的一部分进行温度耦合, 而其它部分不进行温度耦合. 这可以通过对那些不进行恒温的组指定–1的时间常数 \(\t_T\) 来实现. 如果只有体系的一部分进行恒温, 体系最终仍然会收敛到一个NVT体系. 实际上, 有一个建议可尽量降低离散时间步长所造成的温度误差: 如果对水使用了约束, 那么应该只对水的自由度进行恒温, 而不是蛋白质的自由度, 因为蛋白质更高频率的模式可能会导致温度与“真实”温度有更大的偏差, 这里的真实温度指的是使用小的时间步长得到的温度[36].
3.4.9 压力耦合
与温度耦合类似, 体系也可以耦合到一个“压力浴”. GROMACS既支持每步重新缩放坐标与盒矢量的Berendsen算法[25], 扩展系综的Parrinello-Rahman方法[37, 38], 也支持速度Verlet的一种变形, Martyna-Tuckerman-Tobias-Klein (MTTK)方法的压力控制[34]. Parrinello-Rahman和Berendsen方法可以与任何上述的温度耦合方法联用; MTTK只能与Nose-Hoover温度控制方法联用.
Berendsen压力耦合
Berendsen算法会利用矩阵 \(\bi \m\) 重新缩放坐标和盒矢量, 每步或每 \(n_{\text{PC} }\) 步一次, 压力向给定参考压力 \(\bi P_0\) 的弛豫符合一级动力学特征
\[{\rmd{\bi P} \over \rmd t}={\bi P_0- \bi P \over \t_p} \tag{3.59}\]
缩放矩阵 \(\bi \m\) 由下式给出
\[\m_{ij}=\d_{ij} - {n_{\text{PC} } \D t \over 3 \t_p} \b_{ij}\{P_{0ij}-P_{ij}(t)\} \tag{3.60}\]
这里, \(\bi \b\) 为体系的等温压缩系数. 大多数情况下, 它是一个对角矩阵, 且对角线上的值相等, 这个值通常是未知的, 但完全可以采取一个粗略的估计值, 因为 \(\bi \b\) 的值仅影响压力弛豫的非临界时间常数, 而不影响平均压力本身. 1个标准大气压, 300 K条件下, 水的 \(\b= 4.6 \times 10^{-10} \text{Pa}^{-1} = 4.6 \times 10^{-5} \text{bar}^{-1}\), 相应于 \(7.6 \times 10^{-4}\) MD单位(参见第二章). 大多数其它的液体具有与此相近的值. 当缩放具有完全的各向异性时, 必须旋转体系使其服从方程 3.1. 缩放时, 旋转采用一阶近似, 通常小于10-4. 实际的缩放矩阵 \(\bi \m'\) 为
\[\bi \m' =\pmat \m_{xx} & \m_{xy}+\m_{yx} & \m_{xz}+\m_{zx} \\ 0 & \m_{yy} & \m_{yz}+\m_{zy} \\ 0 & 0 & \m_{zz} \\ \epmat \tag{3.61}\]
速度既不缩放, 也不旋转.
在GROMACS中, Berendsen缩放也可以各向同性地进行, 这意味着, 使用对角元素为 \(\text{trace}(\bi P)/3\) 的对角矩阵代替 \(\bi P\). 对存在界面的体系, 半各向同性缩放可能有用. 在这种情况下, 在 \(x/y\) 方向上进行各向同性缩放, 而在 \(z\) 方向上进行独立的缩放. 将 \(x/y\) 或 \(z\) 方向上的压缩系数可以设置为零, 以便只在另一方向上进行缩放.
如果允许完全的各向异性变形并使用约束, 你可能必须使用更缓慢的缩放, 或是减少时间步长以避免约束算法导致的误差. 需要注意的是, 尽管Berendsen控压算法在模拟时能产生正确的平均压力, 但它不能得到精确的NPT系综, 而且目前尚不完全清楚这种方法可能导致的误差.
Parrinello-Rahman压力耦合
若压力或体积的涨落就其自身而言非常重要(例如, 计算热力学性质), 特别是对于小的体系, 弱耦合方案可能存在的一个问题, 这种方案没有很好地定义精确的系综, 模拟的并不是真正的NPT系综.
GROMACS也支持使用Parrinello-Rahman方法[37, 38]的等压模拟, 这种方法类似于Nose-Hoover温控方法, 理论上能给出真正NPT系综. 使用Parrinello-Rahman恒压器, 以矩阵 \(\bi b\) 表示的盒矢量服从矩阵运动方程[2]
\[{\rmd{\bi b^2} \over \rmd{t^2} }=V \bi W^{-1} \bi b^{'-1}(\bi P-\bi P_{ref}) \tag{3.62}\]
其中 \(V\) 代表盒子的体积, \(\bi W\) 为决定耦合强度的矩阵参数. 矩阵 \(\bi P\) 和 \(\bi P_{ref}\) 分别是当前压力和参考压力.
和Nose-Hoover耦合一样, 粒子的运动方程也改变了. 在大多数情况下, 你将联合使用Parrinello-Rahman恒压器与Nose-Hoover恒温器, 为简单起见, 我们这里只给出Parrinello-Rahman导致的变化:
\(\alg {\rmd {\bi r_i^2} \over \rmd {t^2}} &= {\bi F_i \over m_i} -\bi M {\rmd{\bi r_i} \over \rmd t} \tag{3.63} \\ \bi M &= \bi b^{-1} \left[\bi b {\rmd{\bi b'} \over \rmd t}+ {\rmd{\bi b} \over \rmd t} \bi b' \right] \bi b^{'-1} \tag{3.64} \ealg\)
(逆)质量参数矩阵 \(\bi W^{-1}\) 决定了耦合的强度, 以及盒子如何变形. 如果 \(\bi W^{-1}\) 的对应元素为0, 盒子的限制条件(3.1)会自动满足. 由于耦合强度也取决于盒子的大小, 我们更愿意在GROMACS中自动计算盒子的大小. 你只需要在输入文中提供近似的等温压缩系数 \(\bi \b\) 和压力的时间常数 \(\t_P\) (\(L\) 为盒矩阵元素的最大值):
\[(\bi W^{-1})_{ij} = {4 \p^2 \b_{ij} \over 3 \t_p^2 L} \tag{3.65}\]
正如在Nose-Hoover恒温器, 你应该认识到, Parrinello-Rahman时间常数并 不 等同于Berendsen压力耦合算法中使用的弛豫时间. 大多数情况下, 对于Parrinello-Rahman耦合, 你需要使用4–5倍大的时间常数. 如果压力离平衡态非常远, Parrinello-Rahman耦合会导致盒子产生非常大的振荡甚至最终导致运行崩溃. 在这种情况下, 你可能必须增加时间常数, 或(更好的办法)先使用弱耦合方案达到目标压力, 等系统平衡后再切换到Parrinello-Rahman耦合. 此外, 使用蛙跳式算法时, 在整个时间步骤完成之前不能得到 \(t\) 时刻的压力, 因此必须使用上一步中的压力, 这使得算法不是直接可逆的, 并且可能不适合进行高精度的热力学计算.
表面张力耦合
当周期性体系中包含一个以上的相, 且这些相被平行于 \(xy\) 表面的表面所隔离时, 表面张力和压力的 \(z\) 分量会与压力浴相耦合. 目前, 这只适用于GROMACS中的Berendsen压力耦合算法. 平均表面张力 \(\g(t)\) 可以通过法向压力与横向压力之间的差值来计算
\(\alg \g(t) &={1\over n}\int_0^{L_z} \left\{ P_{zz}(z,t) - {P_{xx}(z,t)+P_{yy}(z,t) \over 2} \right\} \rmd z \tag{3.66} \\ &= {L_z\over n}\left\{ P_{zz}(t) - {P_{xx}(t)+P_{yy}(t) \over 2} \right\} \tag{3.67} \ealg\)
其中 \(L_z\) 为盒子的高度, \(n\) 为表面的数目. z方向的压力通过使用 \(\m_{zz}\) 缩放盒子的高度进行校正
\(\alg \D P_{zz} &={\D t \over \t_p} \{P_{0zz}-P_{zz}(t) \} \tag{3.68} \\ \m_{zz} &=1+\b_{zz} \D P_{zz} \tag{3.69} \ealg\)
除缺少 \(1/3\) 这个因子外, 法向压力耦合的校正与此类似. \(z\) 方向上的压力校正, 被用于得到表面张力相对于参考值 \(\g_0\) 的正确收敛值. \(x/y\) 方向盒子长度的校正因子为
\[\m_{x/y}=1+{\D t \over 2 \t_p} \b_{x/y} \left( {n\g_0 \over \m_{zz} L_z} -\left\{P_{zz}(t) + \D P_{zz}-{P_{xx}(t)+P_{yy}(t) \over 2} \right\} \right) \tag{3.70}\]
相比法向压力耦合, \(\b_{zz}\) 的值更关键. 正常情况下不正确的压缩系数仅仅缩放 \(\t_p\), 但对表面张力耦合还会影响表面张力的收敛性. 当 \(b_{zz}\) 设为零时(盒子的高度不变), \(\D P_{zz}\) 也设为零, 以获得正确的表面张力.
MTTK压力控制算法
正如上一节所讲, 蛙跳式积分方法一个缺点在于恒压模拟, 因为计算压力需要整个时间步内的维里和动能, 对蛙跳式积分方法, 这些信息 直到 整个时间步完成之后才能得到.
速度Verlet方法确实可以计算, 但需要额外的全局通讯作为代价, 并计算真正的NPT系综, 忽略任何积分误差.
综合了压力耦合和温度耦合的完整方程, 这里称其为MTTK方程(Martyna-Tuckerman-Tobias-Klein), 取自Martyna等[34]和Tuckerman[39]的论文, . 为方便, 我们引入 \(\e=(1/3) \ln(V/V_0)\), 其中 \(V_0\) 为参考体积. \(\e\) 的动量为 \(v_\e = p_\e/W =\dot{\e}=\dot V/3V\), 并定义 \(\a=1+3/N_{dof}\) (参见参考文献[39])
等压方程为
\(\alg \dot{\bi r}_i &= {\bi p_i \over m_i}+{p_\e \over W} \bi r_i \\ {\dot{\bi p_i} \over m_i} &= {1\over m_i} \bi F_i -\a {p_\e \over W} {\bi p_i \over m_i} \tag{3.71} \\ \dot \e &= {p_\e \over W} \\ {\dot{p_\e} \over W} &={3V \over W}(P_{\text{kin} }-P) +(\a-1)\left( \Sum_{i=1}^N {\bi p_i^2 \over m_i}\right) \\ \tag{3.72} \ealg\)
其中
\[P_{\text{int} } = P_{\text{kin} } - P_{\text{vir} }={1\over 3V}\left[\Sum_{i=1}^N \left({\bi p_i^2 \over 2 m_i}-\bi r_i \cdot \bi F_i \right) \right] \tag{3.73}\]
包含 \(\a\) 的项可保证相空间不可压缩[39]. \(\e\) 加速度项可以改写为
\[{\dot{p_\e} \over W} = {3V \over W}(\a P_{\text{kin} }-P_{\text{vir} }-P) \tag{3.74}\]
对速度项, 这些方程变为
\(\alg \dot{\bi r_i} &= \bi v_i + v_\e \bi r_i \\ \dot{\bi v_i} &= {1\over m_i} \bi F_i -\a v_\e \bi v_i \\ \dot \e &= v_\e \\ \dot{v_\e} &= {3V \over W}(P_{\text{int} }-P)+(\a-1)\left(\Sum_{i=1}^N {1\over2} m_i \bi v_i^2 \right) \\ P_{\text{int} } &= P_{\text{kin} } - P_{\text{vir} }={1\over 3V}\left[ \Sum_{i=1}^N \left({1\over2} m_i \bi v_i^2 -\bi r_i \cdot \bi F_i \right) \right] \tag{3.75} \ealg\)
对于这些方程, 守恒量为
\[H= \Sum_{i=1}^N {\bi p_i^2 \over 2 m_i} +U(\bi r_1, \bi r_2, ..., \bi r_N)+{p_\e \over 2W} +PV \tag{3.76}\]
下一步是添加温度控制, 添加Nose-Hoover链, 并将其添加到恒压器自由度. 令 \(\h\) 为恒压器的Nose-Hoover变量, \(Q'\) 为恒压器的恒温器常数, 我们得到
\(\alg \dot{\bi r}_i &= {\bi p_i \over m_i}+{p_\e \over W} \bi r_i \\ {\dot{\bi p}_i \over m_i} &= {1\over m_i} \bi F_i -\a {p_\e \over W} {\bi p_i \over m_i} - {p_{\x_1} \over Q_1} {\bi p_i \over m_i} \\ \dot \e &= {p_\e \over W} \\ {\dot{p_\e} \over W} &={3V \over W}(\a P_{\text{kin} }-P_{\text{vir} }-P) - {p_{\h_1} \over Q_1'} p_\e \\ \dot{\x}_k &= {p_{\x_k} \over Q_k} \\ \dot \h_k&= {p_{\h_k} \over Q_k'} \\ \dot p_{\x_k} &= G_k -{p_{\x_{k+1} } \over Q_{k+1} } \qquad k=1,...,M-1 \\ \dot p_{\h_k} &= G_k' -{p_{\h_{k+1} } \over Q_{k+1}' } \qquad k=1,...,M-1 \\ \dot p_{\x_M} &= G_M \\ \dot p_{\h_M} &= G_M' \tag{3.77} \ealg\)
其中
\(\alg P_{\text{int} } &= P_{\text{kin} } - P_{\text{vir} } = {1\over 3V}\left[ \Sum_{i=1}^N \left({\bi p_i^2 \over 2m_i}-\bi r_i \cdot \bi F_i \right)\right] \\ G_1 &=\Sum_{i=1}^N {\bi p_i^2 \over 2m_i}-N_f kT \\ G_k &= {p_{\x_{k-1}}^2 \over 2 Q_{k-1}} - kT \;\; k=1,..., M \\ G_1' &= {p_\e^2 \over 2W} -kT \\ G_k' &= {p_{\h_{k-1}}^2 \over 2 Q_{k-1}'} - kT \;\; k=1,..., M \tag{3.78} \ealg\)
现在的守恒量为
\(\alg H &=\Sum_{i=1}^N {\bi p_i^2 \over 2m_i}+U(\bi r_1, \bi r_2, ..., \bi r_N)+{p_\e^2 \over 2W}+PV \\ &+\Sum_{k=1}^M {p_{\x_k}^2 \over 2Q_k} + \Sum_{k=1}^M {p_{\h_k}^2 \over 2Q_k'} + N_f kT \x_1 + kT \Sum_{k=2}^M \x_k +\Sum_{k=2}^M \h_k \tag{3.79} \ealg\)
回到Trotter分解形式, 对压力控制和温度控制[34]我们得到:
\[iL=iL_1+iL_2+iL_{\e,1}+iL_{\e,2}+iL_{\text{NHC-baro} }+iL_{\text{NHC} } \tag{3.80}\]
其中, “NHC-baro”对应于恒压器的Nose-Hoover链, NHC对应于粒子的NHC
\(\alg iL_1 &= \Sum_{i=1}^N \left[{\bi p_i \over m_i}+{p_\e \over W} \bi r_i \right] \cdot {\partial \over \partial \bi r_i} \tag{3.81} \\ iL_2 &= \Sum_{i=1}^N \bi F_i -\a {p_\e \over W} \bi p_i \cdot {\partial \over \partial \bi p_i} \tag{3.82} \\ iL_{\e,1} &= {p_\e \over W} {\partial \over \partial \e} \tag{3.83} \\ iL_{\e,2} &= G_\e {\partial \over \partial p_\e} \tag{3.84} \ealg\)
其中
\[G_\e = 3V(\a P_{\text{kin}} - P_{\text{vir}} -P) \tag{3.85}\]
用Trotter分解, 我们得到
\(\alg \exp(iL\D t) = \;\; & \exp(iL_{\text{NHC-baro} } \D t/2) \exp(iL_{\text{NHC} } \D t/2) \\ &\exp(iL_{\e,2} \D t/2) \exp(iL_2 \D t/2) \\ &\exp(iL_{\e,1} \D t) \exp(iL_1 \D t) \\ &\exp(iL_2 \D t/2) \exp(iL_{\e,2} \D t/2) \\ &\exp(iL_{\text{NHC} } \D t/2) \exp(iL_{\text{NHC-baro} } \D t/2) +O(\D t^3) \tag{3.86} \ealg\)
\(\exp(iL_1 \D t)\) 作用来自于微分方程 \(\dot{\bi r}_i=\bi v_i+v_\e \bi r_i\) 的解, 其中 \(\bi v_i=\bi p_i/m_i\), \(v_\e\) 为常数, 初始条件为 \(\bi r_i(0)\), 在 \(t=\D t\) 时刻进行计算. 这样可以得到
\[\bi r_i(\D t)=\bi r_i(0) e^{v_\e \D t} + \D t \bi v_i(0)e^{v_\e \D t/2} {\sinh(v_\e \D t/2) \over v_\e \D t/2} \tag{3.87}\]
\(\exp(iL_2 \D t/2)\) 作用来自于微分方程 \(\dot{\bi v}_i={\bi F_i \over m_i}-\a v_\e \bi v_i\) 的解, 得到
\[\bi v_i(\D t/2)=\bi v_i(0) e^{-\a v_\e \D t/2} + {\D t\over 2m_i} \bi F_i(0)e^{-\a v_\e \D t/4} {\sinh(\a v_\e \D t/4) \over \a v_\e \D t/4} \tag{3.88}\]
md-vv-avek使用完整步的动能来确定压力控制的压力, 但使用半步平均动能来确定温度, 这可以写为Trotter分解
\(\alg \exp(iL\D t) = \;\; & \exp(iL_{\text{NHC-baro} } \D t/2) \exp(iL_{\e,2} \D t/2)\exp(iL_2 \D t/2) \\ &\exp(iL_{\text{NHC} } \D t/2) \exp(iL_{\e,1} \D t) \exp(iL_1 \D t) \exp(iL_{\text{NHC} } \D t/2) \\ & \exp(iL_2 \D t/2) \exp(iL_{\e,2} \D t/2) \exp(iL_{\text{NHC-baro} } \D t/2) +O(\D t^3) \tag{3.89} \ealg\)
使用约束时, 这些方程会变得更为复杂, 对约束力需要迭代求解每个方程. 对迭代细节的讨论超出了本手册的范围; 我们鼓励读者参看文献[40]中的实现.
温度和压力耦合的不频繁计算
温度和压力的控制需要全局通信来计算的动能和维里, 对大的体系, 如果在每一步都进行会使计算变得十分耗时. 我们可以重排Trotter分解, 给出另一种可逆的辛积分方法, 每 \(n\) 步进行一次而不是每步一次. 当耦合时间步长过大时, 这些新的积分方法将发散, 因为辅助变量积分不收敛. 然而, 在大多数情况下, 长的耦合时间更合适, 因为他们对动力学的扰动小些[34].
使用Nose-Hoover温度控制时, 标准的速度Verlet方法有如下的Trotter展开
\(\alg \exp(iL\D t) \approx \;\; &\exp(iL_{\text{NHC} } \D t/2) \exp(iL_2 \D t/2) \\ &\exp(iL_1 \D t) \exp(iL_2 \D t/2)\exp(iL_{\text{NHC} } \D t/2) \tag{3.90} \ealg\)
如果相对于系统运动, Nose-Hoover链的运动足够慢, 对速度Verlet方法, 我们可以写出一个进行 \(n\) 步的积分方法
\(\alg \exp(iL\D t) \approx \;\; &\exp(iL_{\text{NHC} }(n\D t/2)) [\exp(iL_2 \D t/2) \\ &\exp(iL_1 \D t) \exp(iL_2 \D t/2)]^n \exp(iL_{\text{NHC} }(n\D t/2)) \tag{3.91} \ealg\)
对于压力控制, 这成为
\(\alg \exp(iL\D t) \approx \;\; & \exp(iL_{\text{NHC-baro} }(n\D t/2)) \exp(iL_{\text{NHC} }(n\D t/2)) \\ &\exp(iL_{\e,2}(n\D t/2)) [ \exp(iL_2 \D t/2) \\ &\exp(iL_{\e,1} \D t) \exp(iL_1 \D t) \\ &\exp(iL_2 \D t/2)]^n \exp(iL_{\e,2}(n\D t/2)) \\ &\exp(iL_{\text{NHC} }(n\D t/2)) \exp(iL_{\text{NHC-baro} }(n\D t/2)) \tag{3.92} \ealg\)
其中对盒子体积的积分每步都进行, 但对辅助变量的积分每 \(n\) 步一次.
3.4.10 完整的更新算法
使用蛙跳式积分方法时, 更新速度和坐标的完整算法见图3.9. 步骤4的SHAKE算法在下面进行说明.
GROMACS具有“冻结”(防止运行)选中粒子的规定, 这些粒子必须被定义为“冻结组”. 这是使用 冻结因子 \(\bi f_g\) 实现的, 冻结因子时一个向量, 对每个冷冻组都不相同(参见3.3节). 此向量只包含零(冻结)或1(不冻结). 当我们考虑冻结因子和外部加速度 \(\bi a_h\) 时, 速度的更新算法变为
\[\bi v(t+{\D t \over 2}) = \bi f_g * \l * \left[ \bi v(t-{\D t \over 2}+{\bi F(t) \over m} \D t + \bi a_h \D t \right] \tag{3.93}\]
其中 \(g\) 和 \(h\) 为组索引, 每个原子都不同.

3.4.11 输出步
MD运行的最重要输出是 轨迹文件, 它包含了规则间隔时刻粒子的坐标和(可选的)速度. 轨迹文件包含许多帧, 每帧可能包括位置, 速度和/或力, 以及模拟体积尺寸, 积分步, 积分时间等信息. 时间的解释与所选择的积分方法有关, 如上所述. 对速度Verlet积分方法, 标记时刻 \(t\) 的速度是那个时刻的速度. 对于其他积分方法(如蛙跳式, 随机动力学), 标记时刻 \(t\) 的速度是 \(t-{1\over2}\D t\) 时刻的速度.
由于轨迹文件很长, 不要每一步都保存! 为保留所有信息, 每15步输出一帧就够了, 因为对体系中最大频率的每一周期至少使用了30步, 并且Shannon的采样定理指出, 对带限信号, 最大频率的每一周期进行两次采样就包含了所有可用的信息. 但这样做仍然会得到很大的文件! 所以, 如果对最高频率不感兴趣, 每ps进行10或20此采样就够了. 注意由频闪效应导致的高频运动失真, 这被称为混叠: 较高的频率相对采样频率出现镜像, 显得频率较低.
GROMACS也可以将模拟体系一部分坐标的精度进行降低, 并写入到特殊的压缩格式的轨迹文件. 所有其他的工具可以读取和写入这种格式. 参见7.3节关于如何设置.mdp文件以便使用mdrun此功能的详细信息.
3.5 壳层分子动力学
GROMACS可以使用Dick和Overhauser的壳层模型来模拟极化率[41]. 在这个模型中, 表示电子自由度的壳层粒子通过弹性势连接到原子核上. 在模拟的每一步, 都会对相对于壳层位置的势能进行最小化(见后面). GROMACS中的壳层模型已经成功用于N2[42]和水[43].
3.5.1 优化壳层位置
壳层粒子 \(S\) 上的力 \(\bi F_S\) 可分解为两部分,
\[\bi F_S=\bi F_{bond}+\bi F_{nb} \tag{3.94}\]
其中 \(\bi F_{bond}\) 代表表示极化能量的分量, 通常以简谐势代替, \(\bi F_{nb}\) 为库仑与van der Waals相互作用的加和. 如果我们假定 \(\bi F_{nb}\) 几乎为常数, 就可以解析地导出壳层的最佳位置, 即 \(bi F_S=0\) 的位置. 若壳层S连接到原子A:
\[\bi F_{bond}=k_b(\bi x_S-\bi x_A) \tag{3.95}\]
在迭代求解过程中, 设 \(n\) 次迭代的位置为 \(\bi x_S(n)\), 则在第 \(n\) 次迭代中,
\[\bi F_{nb}=\bi F_S-k_b(\bi x_S(n)-\bi x_A) \tag{3.96}\]
由此壳层的最佳位置符合下面的关系
\[\bi F_S-k_b(\bi x_S(n)-\bi x_A)+k_b(\bi x_S(n+1)-\bi x_A)=0 \tag{3.97}\]
若记
\[\D \bi x_S=\bi x_S(n+1)-\bi x_S(n) \tag{3.98}\]
最终得到
\[\D x_S=\bi F_S/k_b \tag{3.99}\]
这样就得到了优化壳层位置时计算下一步尝试的算法
\[\bi x_S(n+1)=\bi x_S(n)+\bi F_S/k_b \tag{3.100}\]
3.6 约束算法
在GROMACS中可以使用LINCS(默认)或传统的SHAKE方法来施加约束.
3.6.1 SHAKE
SHAKE算法[44]将一组不受约束的坐标 \(\bi r'\) 转变为一组坐标 \(\bi r''\), 使其满足一系列距离约束条件, 使用一组 \(\bi r\) 作为参考,
\[\text{SHAKE}(\bi r' \rightarrow \bi r''; \bi r) \tag{3.101}\]
算法所起的作用与求解一组约束运动方程的Lagrange乘子相同. SHAKE需要指定 相对容差. 算法会继续直到所有的约束都处于相对容差之内. 若由于偏差太大, SHAKE不能重置坐标, 或迭代次数超过指定数目, 会给出错误信息.
假定运动方程必须满足 \(K\) 个完整可积分约束, 表述为
\[\s_k(\bi r_1...\bi r_N)=0; \; k=1...K \tag{3.102}\]
例如 \((\bi r_1-\bi r_2)^2-b^2=0\). 力的定义为:
\[-{\partial \over \partial \bi r_i} \left(V+\Sum_{k=1}^K \l_k \s_k\right) \tag{3.103}\]
其中 \(\l_k\) 为Lagrange乘子, 必须求解它们以满足约束方程. 上面求和的第二部分决定了 约束力 \(\bi G_i\), 定义为:
\[\bi G_i=-\Sum_{k=1}^K \l_k \opar {\s_k}{\bi r_i} \tag{3.104}\]
在蛙跳式或Verlet算法中, 由约束力引起的位移为 \((\bi G_i/m_i)(\D t)^2\). 求解Lagrange乘子(进而位移)需要求解一组二度耦合的方程, 这可使用SHAKE方法迭代求解. 对于刚性水分子的特殊情况, 这种模拟构成了超过了80%的模拟体系, 我们已经实现了SETTLE算法(见5.5节)[45].
对速度Verlet, 必须施加额外的约束, 以约束第二个半速度步的速度, 并去除平行于键向量的任何速度分量, 这一步骤被称为RATTLE, Andersen的论文中对其有更详细的论述[46].
3.6.2 LINCS
LINCS算法
在未约束的一步更新之后, LINCS算法会将键重置为它们的正确长度. 这个方法不进行迭代, 总是包含两个步骤. 尽管LINCS方法基于矩阵, 但并不需要进行矩阵乘法. LINCS方法比SHAKE方法更稳定, 也更快, 但只能用于键约束和孤立的键角约束, 如OH的质子键角. 由于其稳定性, LINCS特别适用于Brown动力学. LINCS有两个参数, 在后文的参数节中将会解释. 并行版本的LINCS, P-LINCS, 将在3.17.3节介绍.
LINCS公式
考虑 \(N\) 个粒子的体系, 粒子位置由 \(3N\) 向量 \(\bi r(t)\) 给出. 分子动力学中的运动方程由牛顿定律给出:
\[{\mathrm d^2 \bi r \over \mathrm d t^2} = \bi M^{-1} \bi F \tag{3.105}\]
其中 \(\bi F\) 为 \(3N\) 个力向量, \(\bi M\) 为 \(3N \times 3N\) 的对角矩阵, 包含了粒子的质量. 体系受到 \(K\) 个与时间无关的约束方程
\[g_i(\bi r) =|\bi r_{i_1}-\bi r_{i_2}|-d_i=0 \;\; i=0,...,K \tag{3.106}\]
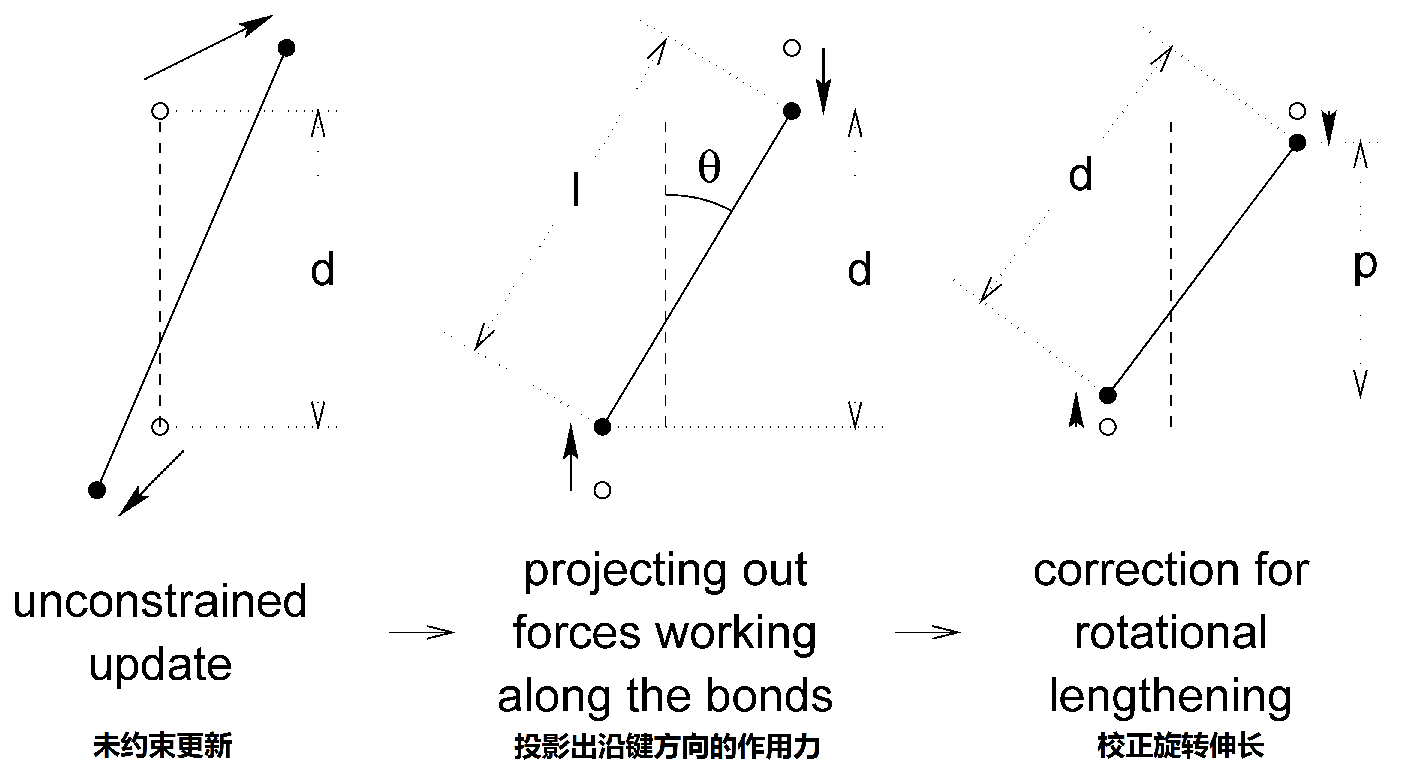
在数值积分方案中, LINCS会在一个未约束的更新之后施加, 如SHAKE一样. LINCS算法分两步工作(见图3.10). 在第一步中, 新键到旧键的投影被设置为零, 在第二步中, 对因旋转导致的键伸长进行校正. 第一步与第二步的计算非常相似. 算法的完整推导见[47], 这里只给出第一步的一个简短说明.
对约束方程的梯度矩阵使用新的记号, 记为
\[B_{hi}=\opar {g_H}{r_i} \tag{3.107}\]
注意 \(\bi B\) 为 \(K\times 3N\) 的矩阵, 包含了约束的方向. 下列方程显示了新的约束坐标 \(\bi r_{n+1}\) 与未约束坐标 \(\bi r_{n+1}^{unc}\) 的关系
\[\bi r_{n+1}=(\bi I-\bi T_n \bi B_n)\bi r_{n+1}^{unc}+\bi T_n \bi d = \\ \bi r_{n+1}^{unc}-\bi M^{-1}\bi B_n (\bi B_n \bi M^{-1} \bi B_n^T)^{-1} (\bi B_n \bi r_{n+1}^{unc}-\bi d) \tag{3.108}\]
其中 \(\bi T=\bi M^{-1}\bi B^T(\bi B\bi M^{-1}\bi B^T)^{-1}\). 由方程3.105, 3.106推导此方程的过程可参见[47].
第一步并未将实际键的长度设置为需要的长度, 而是将新键投影到旧键的方向上. 为校正键 \(i\) 的旋转, 键在原先方向上的投影 \(p_i\) 被设置为
\[p_i=\sqrt{2d_i^2-l_i^2} \tag{3.109}\]
其中 \(l_i\) 为经第一步投影后键的长度. 校正后的位置为
\[\bi r_{n+1}^* =(\bi I -\bi T_n\bi B_n)\bi r_{n+1}+\bi T_n \bi p \tag{3.110}\]
对旋转效应的校正实际上是一个迭代过程, 但在MD过程中只进行了一步. 对每一约束, 经过这一校正后, 约束的相对偏差将小于0.0001. 在能量最小化中, 这可能不够精确, 因此, 迭代次数被设置为展开的阶数(见后文).
约一半的CPU时间被用于对约束耦合矩阵 \(\bi B_n \bi M^{-1}\bi B_n^T\) 进行求逆, 而且必须每步进行一次. \(K\times K\) 矩阵的对角元素为 \(1/m_{i_1}+1/m_{i_2}\). 只有当两个键相连时非对角元素才不为零, 而是 \(\cos\f/m_c\), 其中 \(m_c\) 为连接两个键的原子质量, \(\f\) 为键之间的夹角.
使用幂展开方法对矩阵 \(\bi T\) 求逆. 为此引入 \(K\times K\) 的矩阵 \(\bi S\), 其元素为矩阵 \(\bi B_n \bi M^{-1}\bi B_n^T\) 对角元素平方根的倒数. 这一矩阵可用于将耦合矩阵的对角元素变换为1:
\[(\bi B_n \bi M^{-1}\bi B_n^T)^{-1}=\bi S \bi S^{-1} (\bi B_n \bi M^{-1}\bi B_n^T)^{-1} \bi S^{-1} \bi S \\ =\bi S (\bi S \bi B_n \bi M^{-1}\bi B_n^T \bi S)^{-1} \bi S=\bi S(\bi I-\bi A_n)^{-1} \bi S \tag{3.111}\]
矩阵 \(\bi A_n\) 是对称的稀疏矩阵, 对角元素中含有零, 因此可以使用一个简单的技巧来计算其逆矩阵
\[(\bi I-\bi A_n)^{-1}=\bi I+\bi A_n+\bi A_n^2+\bi A_n^3+... \tag{3.112}\]
这种求逆方法只有当所有 \(\bi A_n\) 本征值的绝对值都小于1时才使用. 对只含有键约束的分子, 其连接度非常低, 这个条件总是成立, 即使有环状结构出现也是一样. 对含有键角约束的分子, 可能会有问题. 使用额外的距离约束来约束键角, 可以引入多个小的环状结构. 这样分子的连接度变高, 本征值变大. 因此LINCS方法 不能 应用于耦合键角约束.
对所有键都进行约束的分子, \(\bi A_n\) 的本征值约为0.4, 这意味着在展开方程3.112中, 每增大一个阶数, 偏差会下降为原来的0.4. 但对相对孤立的三角约束, 最大的本征值大约为0.7. 当使用额外的角约束移除醇类基团中含氢的键角振动, 或当使用LINCS约束水分子, 如使用柔性约束时, 会导致这些三角约束出现. 这些三角约束的收敛速度比其他约束慢两倍. 因此, 从GROMACS 4.0版本开始, 一些额外的项被添加到这些三角约束的展开中
\[(\bi I-\bi A_n)^{-1} \approx \bi I+\bi A_n+...+\bi A_n^{N_i}+\left(\bi A_n^*+...+\bi A_n^{*N_i} \right) \bi A_n^{N_i} \tag{3.113}\]
其中 \(N_i\) 为正常的展开阶数, \(\bi A^*\) 只包含 \(\bi A\) 中处于刚性三角耦合约束内的元素, 所有其他元素为零. 使用这种方法, 角约束的精度接近其他约束的精度, 同时确定展开所需要的一系列矩阵矢量乘法只需要对几个约束耦合进行. 这一过程在P-LINCS的论文[48]中有说明.
LINCS参数
LINCS精度取决于展开方程3.112中矩阵的数目. 对MD计算四阶展开就足够了; 对Brown动力学, 使用大的时间步长时, 可能需要八阶展开. 展开阶数是*.mdp文件中的一个参数. LINCS的实现方式使得其算法不可能失败. 即使不可能重置约束时, LINCS也将创建一个尽可能满足约束构型. 然而, 当在某一步中键的旋转超过了预先定义的角度时, LINCS会给警告. 这一角度用户可以在*.mdp文件中设置.
3.7 模拟退火
GROMACS支持众所周知的模拟退火方法. 你甚至可以独立地将多个原子组和任意数目的参考温度进行耦合, 参考温度在模拟中会改变. 对温度耦合中的每一组, 退火是通过简单地改变当前的参考温度实现的. 因此, 实际的弛豫和耦合性质取决于你使用的热浴类型与耦合强度. 由于参考温度会变化, 请务必记住体系温度 不会 瞬时达到参考值–你必须考虑到耦合算法内在的弛豫时间. 如果退火参考温度的改变快于温度弛豫, 当它们之间相差过大时, 模拟可能会崩溃.
退火策略是对每个组指定一系列相应的时间和参考温度. 你还可以选择只使用单个序列(退火完成后温度将耦合到最后的参考值), 或是使用周期性退火, 当退火序列完成后重新从第一个参考温度开始. 在模拟中, 你可以混合配合使用两种退火类型和不退火的组.
3.8 随机动力学
随机或速度Langevin动力学在牛顿运动方程中增加了摩擦项和噪声项:
\[m_i {\mathrm d^2 \bi r_i \over \rmd {t^2} } = -m_i \g_i {\rmd {\bi r_i} \over \rmd t}+\bi F_i(\bi r)+\mathring{\bi r}_i \tag{3.114}\]
其中 \(\g_i\) 为摩擦常数[1/ps], \(\mathring {\bi r}_i\) 为噪声过程, 满足 \(\langle \mathring r_i(t) \mathring r_j(t+s) \rangle=2m_i \g_i k_B T \d(s)\d_{ij}\). 当与体系的时间尺度相比, \(1/\g_i\) 较大时, 随机动力学可视为具有随机温度耦合的分子动力学. 与使用Berendsen温度耦合的MD相比, SD的优势在于它产生的系综是已知的. 模拟真空中的体系时, SD还有另外一个优点: 对整个平动转动自由度不存在误差累积. 当 \(1/\g_i\) 小于体系的时间尺度时, 动力学与MD完全不同, 但取样仍然正确.
在GROMACS中有两种算法可用于积分方程3.114: 简单有效的方法和更复杂的蛙跳式算法[49]. 后一方法现在已经废弃. 这两种积分方法的精度等价于常规MD的蛙跳式积分方法与速度Verlet积分方法的精度, 不同在于存在约束时复杂SD积分方法的采样温度稍微过高(尽管误差小于使用整步速度动能项的速度Verlet积分方法). 简单积分方法几乎与等同于常用的离散Langevin方程方法, 但以脉冲方式施加摩擦项与速度项[50]. 简单积分方法如下:
\[\alg \bi v' &= \bi v(t-{1\over2}\D t)+{1\over m}\bi F(t) \D t \tag{3.115} \\ \D \bi v &= -\a \bi v'(t+{1\over2}\D t)+\sqrt{ {k_B T\over m}(1-\a^2)} \bi r_i^G \tag{3.116} \\ \bi r(t+\D t) &= \bi r(t)+ \left(\bi v'+{1\over2}\D t\right) \D t \tag{3.117} \\ \bi r(t+{1\over2}\D t) &= \bi v'+\D \bi v \tag{3.118} \\ \a &= 1-e^{-\g \D t} \tag{3.119} \ealg\]
其中 \(\bi r_i^G\) 为服从高斯分布的噪声, 其 \(\m=0\), \(\s=1\). 算法首先在无摩擦与噪声的情况下更新整个时间步的速度, 获得 \(\bi v'\), 这完全与蛙跳式的常规更新相同. 然后在 \(t+\D t\) 步以脉冲方式施加摩擦与噪声. 这种方案的优点在于依赖速度的项在整个时间步中都起作用, 由于对力的积分取决于坐标与速度, 这样就使得方案对力进行正确积分很简单, 如在约束和耗散粒子动力学(DPD, dissipative particle dynamics, 还未实现)情况下. 有约束时, 坐标更新方程3.117会被划分为常规的蛙跳式更新与 \(\D \bi v\). 这些更新都完成后, 再对坐标和速度施加约束.
在已废弃的复杂方法中, 在每个积分步对每个自由度需要四个高斯随机数, 有约束时, 每个积分步坐标需要约束两次. 取决于力的计算代价, 这可能会占用显著一部分模拟时间. 精确地对随机动力学进行继续运行是不可能的, 因为在模拟过程中没有存储随机数产生器的状态.
当使用SD控温时, \(\g\) 的合适值可取0.5 ps-1, 因为这样得到的摩擦低于水的内摩擦, 同时仍能提供有效的控温.
3.9 Brown动力学
在高摩擦的极限情况下, 随机动力学退化为Brown动力学, 也被称为位置Langevin动力学. 它施加于过阻尼体系, 即惯性效应可忽略的体系. 方程为
\[{\mathrm d \bi r_i \over \rmd t}={1\over \g_i} \bi F_i(\bi r)+\mathring {\bi r}_i \tag{3.120}\]
其中 \(\g_i\) 为摩擦系数[amu/ps], \(\mathring {\bi r}_i(t)\) 为噪声过程, 满足 \(\langle \mathring r_i(t) \mathring r_j(t+s) \rangle=2\d(s)\d_{ij} k_B T/\g_i\). 在GROMACS中, 使用简单的显示方案进行上面的方程进行积分:
\[\bi r_i(t+\D t) = \bi r_i(t) +{\D t\over \g_i} \bi F_i(\bi r(t)) +\sqrt{ 2k_B T{\D t\over \g_i} } \bi r_i^G \tag{3.121}\]
其中 \(\bi r_i^G\) 为服从高斯分布的噪声, 其 \(\m=0\), \(\s=1\). 摩擦系数 \(\g_i\) 可以取为对所有粒子相同, 或者取为 \(\g_i=m_i \g_i\), 其中的摩擦系数 \(\g_i\) 对不同组的原子可取不同值. 由于假定体系处于过阻尼状态, 因此可以使用大的时间步长. 应使用LINCS方法进行约束, 因为SHAKE方法对大的原子位移不收敛. BD是mdrun程序的一个选项.
3.10 能量最小化
GROMACS中的能量最小化可以使用最速下降, 共轭梯度, 或L-BFGS(有限内存的Broyden-Fletcher-Goldfarb-Shanno准牛顿最小化, 我们倾向于使用简称). EM只是mdrun程序的一个选项.
3.10.1 最速下降
尽管最速下降方法确实不是最有效的搜索算法, 它很稳健, 并且易于实现.
定义代表所有 \(3N\) 个坐标的向量 \(\bi r\). 初始时, 必须给出的最大位移值 \(h_0\) (例如0.01 nm).
首先计算力 \(\bi F\) 和势能. 新位置的计算方法如下:
\[\bi r_{n+1}=\bi r_n+{\bi F_n \over \max(|\bi F_n|)} h_n \tag{3.122}\]
其中 \(h_n\) 为最大位移, \(\bi F_n\) 为力, 也即势能 \(V\) 的负梯度. \(\max(|\bi F_n|)\) 表示力分量绝对值的最大值. 再次计算新位置的力与能量,
- 若 \(V_{n+1} \lt V_n\), 则接受新位置, 令 \(h_{n+1}=1.2h_n\)
- 若 \(V_{n+1} \ge V_n\), 则拒绝新位置, 令 \(h_{n+1}=0.2h_n\)
当力的计算次数达到用户指定的数目(如100), 或力(梯度)分量绝对值的最大值小于设定值 \(\e\) 后, 算法停止. 由于力的截断会使能量计算产生一些噪声, 停止条件不应该设得过高, 以免算法迭代无法结束. \(\e\) 的合理值可以根据简谐振子在温度 \(T\) 下的受到的根均方力 \(f\) 来估计, 其值为
\[f=2\p\n \sqrt{2mkT} \tag{3.123}\]
其中 \(\n\) 为振子频率, \(m\) 为(约化)质量, \(k\) 为Boltzmann常数. 对波数为100 cm-1, 质量为10 原子单位, 温度 1 K时的弱振子, \(f=7.7\) kJ mol-1 nm-1. \(\e\) 的值在1到10之间是可以接受的.
3.10.2 共轭梯度
共轭梯度在最小化早期慢于最速下降, 但靠近能量最低点时更高效. 方法的参数和停止条件与最速下降相同. 在GROMACS中, 共轭梯度不能与约束一起使用, 包括用于刚性水的SETTLE算法[45], 因为还未实现. 若体系中存在水分子, 必须使用柔性水模型, 这可以在*.mdp文件中利用define = -DFLEXIBLE指定.
这真的不是一个限制, 因为只有在简正模式分析前的能量最小化中才需要共轭梯度的精度, 简正分析时不能使用约束. 对大多数其他目的, 最速下降足够高效.
3.10.3 L-BFGSD
原始的BFGS算法会逐步产生更好的逆Hess矩阵的近似, 并将体系移动到当前的估计的最小点. 这种方法需要的内存正比于粒子数的平方, 因此实用中不能用于大体系如生物分子. 作为替代, 我们使用了Nocedal的L-BFGS算法[51, 52]. 它使用来自前一步的固定数目的校正得到近似的逆Hess矩阵. 这种滑动窗技术几乎与原始方法一样有效, 但所需内存要少得多–正比于粒子数与校正步数的乘积. 实用中, 我们发现它比共轭梯度收敛得更快, 但由于存在校正步, 此方法还未并行化. 也需要指出, 切换或移位相互作用通常可以提高收敛性, 因为明显的截断意味着当前坐标下的势能函数与前一步用于构建逆Hess矩阵近似的势能函数稍有不同.
3.11 简正模式分析
GROMACS可以进行简正模式分析[53, 54, 55], 计算是通过对角化质量加权的Hess矩阵 \(H\) 进行的:
\[\alg R^T M^{-1/2} H M^{-1/2} R &= \text{diag}(\l1, ..., \l_{3N}) \tag{3.124} \\ \l_i &= (2\p \w_i)^2 \tag{3.125} \ealg\]
其中 \(M\) 包含了原子质量, \(R\) 的列为本征向量, \(\l_i\) 为本征值, \(\w_i\) 为相应的频率.
首先需要计算Hess矩阵, 它是一个 \(3N\times 3N\) 的矩阵, 其中 \(N\) 为原子数,
\[H_{ij}={\partial^2 V \over \partial x_i \partial x_j} \tag{3.126}\]
其中 \(x_i\) 和 \(x_j\) 代表原子的x, y或z坐标. 实际计算时并不使用上面的方程, 而是根据得到的力, 利用数值方法计算Hess矩阵
\[\alg H_{ij} &= -{f_i(\bi x+h\bi e_j) - f_i(\bi x-h\bi e_j) \over 2h} \tag{3.127} \\ f_i &=-\opar V {x_i} \tag{3.128} \ealg\]
其中 \(\bi e_j\) 为 \(j\) 方向的单位向量. 应当指出, 对通常的简正模式计算, 在计算Hess矩阵前需要进行彻底的能量最小化, 需要的能量容差取决于体系的类型, 粗略的指示值为0.001 kJ mol-1. 应当使用共轭梯度或L-BFGS方法进行能量最小化, 并使用双精度版本.
在这些计算中会涉及多个GROMACS程序. 首先应该使用mdrun进行能量最小化, 其次再使用mdrun计算Hess矩阵. 注意, 创建运行输入文件时, 应使用来自全精度轨迹文件中的最小化的构型, 因为结构文件不够精确. g_nmeig程序进行对角化计算, 并将简正模式按其频率进行排序. mdrun和g_nmeig都应当使用双精度版本. 可以使用g_anaeig程序分析简正模式. 要创建任意温度下的结构系综中的任意一组简正模式, 可使用g_nmens程序. 关于简正模式分析及其相关的主成分分析(见8.10节)的概述可参见[56].
3.12 自由能计算
3.12.1 慢增长方法
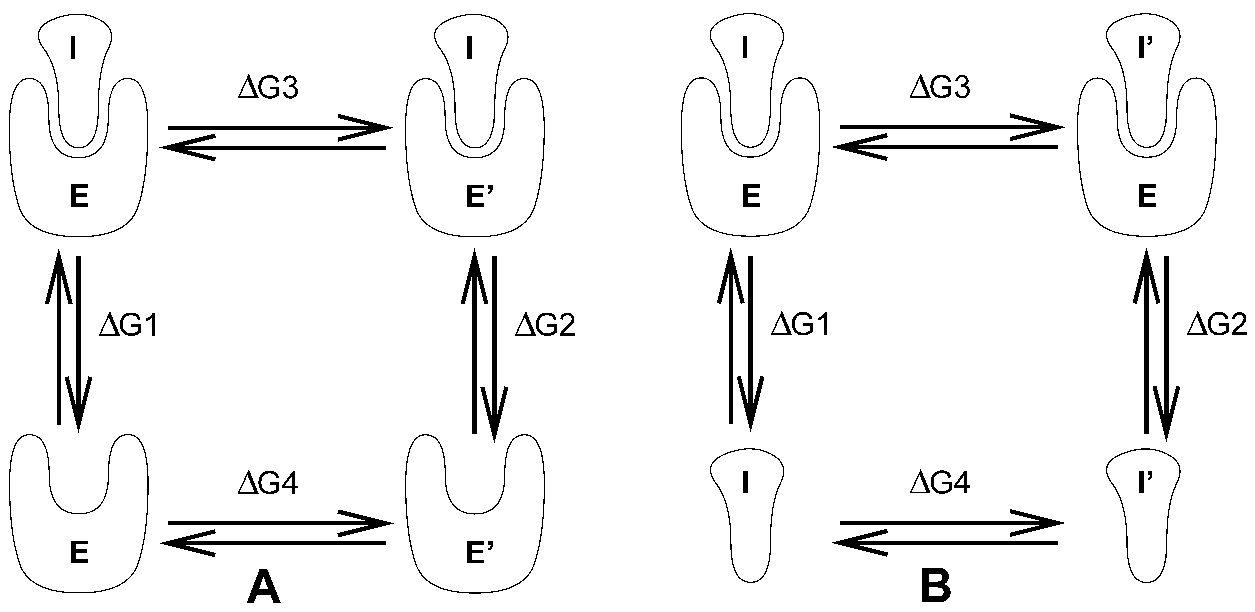
GROAMCS可使用几种不同的方法计算自由能, 其中包括“慢增长”方法. 自由能计算的一个例子是计算抑制剂I分别与酶E, 突变后的酶E’结合时的自由能差值. 对这样的大体系, 利用计算机模拟来进行对接计算是不可行的, 即便是在合理的计算时间内以合理的计算精度模拟抑制剂从酶中释放的过程, 也是不可行的. 然而, 如果我们考虑图3.11 A中的热力学循环, 可得到
\[\D G_1-\D G_2 =\D G_3 -\D G_4 \tag{3.129}\]
若对左边的项感兴趣, 我们也可以同样好地计算右边的项.
如果我们要计算两个抑制剂I和I’与酶E’结合时的自由能差值(图3.11 B), 我们仍然可以使用方程3.129来计算所需要的性质.
在GROMACS中可以利用“慢增长”方法计算两个分子物种之间的自由能差值. 不同分子物种之间的这种自由能差值没有物理意义, 但利用热力学循环, 可由它们获得有意义的量. 这种方法要求在模拟中体系的哈密顿量缓慢地从描述一个体系(A)转变到描述另一个体系(B). 变化必须足够缓慢. 以保证体系在这个过程中仍保持平衡状态. 若能满足这些要求, 变化是可逆的, 并且从B到A的慢增长模拟与从A到B的慢增长模拟会得到同样的结果(但符号相反). 这是一个有用的核查方法, 但用户应当心, 正向与反向增长结果的相等并不能确保结果的正确性.
对哈密顿量所需的修改是通过将 \(H\) 作为 耦合参数 \(\l\) 的函数实现的: \(H=H(p,q;\l)\). 这样 \(\l=0\) 描述体系A, \(\l=1\) 描述体系B:
\[H(p,q;0)=H^A(p,q); \;\; H(p,q;1)=H^B(p,q) \tag{3.130}\]
在GROMACS中, \(\l\) 依赖的函数形式对各种力场贡献是不同的, 对此的说明请参看4.5节.
Helmholtz自由能 \(A\) 与 \(N\), \(V\), \(T\) 系综的配分函数 \(Q\) 有关, 这一系综被认为是等容等温MD模拟产生的平衡系综. 一般更有用的Gibbs自由能 \(G\) 与 \(N\), \(P\), \(T\) 系综的配分函数 \(\D\) 有关, 这一系综被认为是等压等温MD模拟产生的平衡系综.
\[\alg A(\l) &= -k_B T\ln Q \tag{3.131} \\ Q &= c\iint \exp[-\b H(p,q;\l)] \rmd p \rmd q \tag{3.132} \\ G(\l) &= -k_BT\ln \D \tag{3.133} \\ \D &= c\iiint \exp[-\b H(p,q;\l)-\b pV] \rmd p \rmd q \rmd V \tag{3.134} \\ G &= A+pV \tag{3.135} \ealg\]
其中 \(\b=1/(k_B T)\), \(c=(N!h^{3N})^{-1}\). 这些对相空间的积分不能由模拟得到, 但可以计算它们对 \(\l\) 的导数作为系综平均:
$${\rmd A \over \rmd \l}={\iint (\partial H/\partial \l) \exp[-\b H(p,q;\l)] \rmd p \rmd q \over \iint \exp[-\b H(p,q;\l)] \rmd p \rmd q} = \left< \opar H \l \right>_{NVT;\l} \tag{3.136} $$
在 \(N\), \(p\), \(T\) 系综中的关系与此类似. A和B之间的自由能差值可通过积分对 \(\l\) 的导数获得:
\[\alg A^B(V,T)-A^A(V,T) &= \int_0^1 \left< \opar H \l \right>_{NVT;\l} \rmd \l \tag{3.137} \\ G^B(p,T)-G^A(p,T) &= \int_0^1 \left< \opar H \l \right>_{NpT;\l} \rmd \l \tag{3.138} \\ \ealg\]
若要计算 \(G^B(p,T)-G^A(p,T)\), 自然的选择是等压模拟. 然而, 也可以从等容的慢增长模拟计算这个量, 模拟由压力为 \(p\) 体积为 \(V\) 的体系A开始, 到压力为 \(p_B\) 的体系B结束, 并进行下面的小(但原则上精确)校正:
\[G^B(p)-G^A(p) = A^B(V)-A^A(V)-\int_p^{p^B} [V^B(p')-V] \rmd {p'} \tag{3.139}\]
这里的记号中忽略了温度 \(T\). 这一校正粗略地等于 \(-{1\over2}(p^B-p)\D V=(\D V)^2/(2 \k V)\), 其中 \(\D V\) 为 \(p\) 时的体积变化, \(\k\) 为等温压缩率. 这一校正通常很小, 例如, 等容情况下, 在1000个水分子的体系中凭空产生一个水分子增加的额外压力最大为22 bar, 但对Helmholtz自由能的校正只有–1 kJ mol-1.
在直角坐标系中, 哈密顿量的动能项只取决于动量, 可独立进行积分, 并且实际上可从方程中去除. 当质量不变时, 动能对自由能完全没有贡献. 当质量变化时, 对自由能的累计贡献为 \(-{3\over2}k_B T\ln(m^B/m^A)\). 注意 这只对无约束的情况适用.
3.12.2 热力学积分
GROMACS也可以在一个模拟中对方程3.137或3.138从A到B的整个范围内进行积分. 然而, 若变化太大, 采样可能不充分, 用户可能更倾向于在仔细选择的中间的 \(\l\) 值上精确地确定 \(\langle \rmd G/\rmd \l \rangle\) 的值. 通过将步长delta_lambda设定为零, 这很容易实现. 每一模拟都可以先进行平衡, 由 \(\partial H/\partial \l\) 的涨落可以得到每个 \(\langle \rmd G/\rmd \l \rangle\) 值的合适的误差估计. 然后, 可以通过适当的数值积分获得总的自由能变化.
GROMACS现在也支持使用g_bar程序计算从状态A转变到状态B的 \(\D G\) 值, 计算时利用BAR(Bennett’s Acceptance Ratio)方法. 相同的数据也可用MBAR[58]方法来计算自由能, 但目前分析时需要来自外部pybar程序包中的工具, 可从https://SimTK.org/home/pymbar下载.
力场贡献与 \(\l\) 的依赖关系将在4.5节详细讨论.
3.13 副本交换动力学
副本交换分子动力学(REMD, replica exchange molecular dynamics)是一种加速抽样的方法, 可用于任何类型的模拟, 特别适用于不同构象之间存在较高能量势垒的情况. 它对同一体系处于不同温度下的多个副本进行模拟, 并以一定的时间间隔随机地完全交换两个副本的状态, 交换的概率为:
$$ P(1 \leftrightarrow 2)=\min\left(1, \exp\left[ \left({1\over k_B T_1} -{1\over k_B T_2} \right)(U_1-U_2) \right] \right) \tag{3.140}$$
其中 \(T_1\) 和 \(T_2\) 为参考温度, \(U_1\) 和 \(U_2\) 分别为副本1和2的瞬时势能. 交换后, 使用 \((T_1/T_2)^{\pm 0.5}\) 对速度进行缩放, 并在下一步进行近邻搜索. 这方法将快速采样和最高温度频繁跨垒方法结合起来, 在所有不同温度下都使用了正确的玻耳兹曼抽样[59, 60]. 由于随着温差的增大概率下降非常迅速, 我们只会尝试交换相邻的温度. 在一步中我们不应尝试对所有可能的副本对进行交换. 例如, 如果交换副本1和2, 交换副本2和3的机会不仅取决于副本2和3的能量, 还取决于副本1的能量. 在GROMACS中这个问题的解决方法是, 在“奇数”次尝试试着交换所有的“奇数”副本对, 在“偶数”次尝试试着交换所有的“偶数”副本对. 如果我们有四个按温度排序的副本: 0, 1, 2和3, 并且每1000步尝试进行一次交换, 那么将会在1000, 3000等步尝试对副本对0–1和2–3进行交换, 在2000, 4000等步尝试对副本对1–2进行交换.
应该如何选择温度呢? 能量差可以写成:
$$ U_1-U_2=N_{df} {c \over2} k_B (T_1-T_2) \tag{3.141}$$
其中 \(N_{df}\) 为一个副本的总自由度数, 对简谐势 \(c\) 为1, 对蛋白质/水体系 \(c\) 为2左右. 如果 \(T_2=(1+\e)T_1\) 则概率变为:
\[P(1 \leftrightarrow 2)=\exp\left(-{\e^2 c N_{df} \over 2(1+\e)} \right) \approx \exp\left(-\e^2 {c\over2}N_{df}\right) \tag{3.142}\]
这样, 对于大小为 \(e^{-2} \approx 0.135\) 的概率, 可得到 \(\e \approx 2/\sqrt{c N_{df} }\). 对所有键都进行约束时, \(N_{df}\approx 2 N_{atoms}\), 这样对于 \(c=2\) 我们应选择的 \(\e\) 为 \(1/\sqrt{N_{atoms} }\). 然而, 当我们使用压力耦合时会出现一个问题. 更高温时密度会下降, 并导致能量增加[61], 这些情况我们需要考虑到. GROMACS网站提供了一个被称为“REMD calculator”的计算器, 它可以根据你输入的温度范围和原子数给出一组温度.
Okabe等人提出了等压等温系综的REMD扩展[62]. 他们将交换概率修改为:
$$ P(1 \leftrightarrow 2)=\min\left(1, \exp\left[ \left({1\over k_B T_1} -{1\over k_B T_2} \right)(U_1-U_2) + \left({P_1\over k_B T_1} -{P_2\over k_B T_2} \right)(V_1-V_2)\right] \right) \tag{3.143}$$
其中 \(P_1\) 和 \(P_2\) 为各自的参考压力, \(V_1\) 和 \(V_2\) 为模拟中各自的瞬时体积. 在大多数情况下, 体积的差别很小以至于可以忽略第二项. 只有在 \(P_1\) 和 \(P_2\) 之间相差很大或者存在相变的情况下第二项才起作用.
GROMACS也支持哈密顿量副本交换. 在哈密顿量副本交换中, 每个副本的哈密顿量不同, 并根据模拟指定的自由能途径进行定义. 用来维持正确系综概率的交换概率为:
$$ P(1 \leftrightarrow 2)=\min\left(1, \exp\left[ \left({1\over k_B T_1} -{1\over k_B t_2} \right)( (U_1(x_2)-U_1(x_1)) +(U_2(x_1)-U_2(x_2)) )\right] \right) \tag{3.144}$$
各自的哈密顿量由GROMCAS内置的自由能函数定义, 并在不同 \(\l\) 值之间进行交换, \(\l\) 在mdp文件中定义.
也可以同时进行哈密顿量副本交换和温度副本交换, 使用的接受标准为:
$$ P(1 \leftrightarrow 2)=\min\left(1, \exp\left[ \left({1\over k_B T_1} - \right)({U_1(x_2)-U_1(x_1) \over k_B T} + {U_2(x_1)-U_2(x_2) \over k_B T_2})\right] \right) \tag{3.145}$$
GROMACS还实现了吉布斯抽样副本交换[63]. 在吉布斯抽样副本交换中, 会测试所有可能交换的副本对, 并允许交换不相邻的副本.
吉布斯抽样副本交换不需要额外的势能计算. 然而, 在吉布斯抽样副本交换中存在额外的通讯成本, 对一些排列, 肯定会发生超过一轮的交换. 在某些情况下, 这些额外的通讯成本可能会影响效率.
mdrun程序的包含了所有不同副本交换方法的选项. 由于算法中内在的并行化, 只有安装了MPI时候才能运行副本交换模拟. 为提高效率, 每个副本可以在一个独立的队列上运行. 想了解如何使用这些多节点功能, 可以参考mdrun的帮助文档.
3.14 主成分动力学抽样
蛋白质主成分动力学(参见8.10节)的结果可用于指导MD模拟. 基本思想是, 我们可以从初始MD模拟(或源自其他途径)中获得拥有最大振幅的集约涨落. 对沿一个或多个这些集约模式的那些位置, 在接下来的(第二次)MD模拟中可以使用约束, 约束时可根据不同的目的使用不同的方法. 例如, 可以固定沿一个特定模式的位置以监测在此位置坐标上的平均力(自由能梯度). 另外一个应用是提高相对于普通MD的抽样效率[64, 65]. 在这种情况下, 与蛋白质通常采用的类扩散途径相比, 对体系构型空间的采样更系统.
另外一个提高抽样效率的可能方法是洪泛方法, 将洪泛势添加到一些(集约)自由度上, 以将体系排除到在某些相空间区域之外[66].
主成分动力学抽样或洪泛方法的步骤如下. 首先使用协方差分析(g_covar)或者简正模式分析(g_nmeig)确定特征向量和特征值. 然后将这些信息用于make_edi, 这个命令有很多用于选择向量和设定参数的选项, 请参考gmx make_edi -h. 最后将生成的edi输入文件传递给mdrun.
3.15 扩展系综动力学
在扩展系综模拟[67]中, 坐标和热力学系综都可以被视为构型变量进行抽样. 任何给定状态的概率可写为:
$$ P(\vec x, k) \propto \exp(-\b_k U_k +g_k) \tag{3.146}$$
其中 \(\b_k={1\over k_B T_k}\) 为对应于第 \(k\) 个热力学状态 \(\b\), \(g_k\) 为用户定义的对应于第 \(k\) 个状态的权重因子. 因此, 这一空间是 混合, 通用, 或 扩展 的系综, 是对多个热力学系综同时抽样得到的. \(g_k\) 用于为扩展系综中的每个子系综指定权重, 既可以是固定的, 也可以由迭代程序确定. 通常选择的 \(g_k\) 集合对每个热力学系综会给出相同的概率, 在这种情况下, \(g_k\) 等于无量纲的自由能, 但根据需要也可以将它们设定为任意值. 在mdp选项列表中有好几种算法可以用来平衡这些权重.
在GROMACS中, 这个空间通过交替地在 \(k\) 和 \(\vec x\) 方向上采样得到. \(\vec x\) 方向的采样是由标准的分子动力学采样完成; 不同热力学状态之间的采样由Monte Carlo完成, 且支持几种不同的Monte Carlo移动方法. \(k\) 状态可以根据温度的不同进行定义, 或根据自由能 \(\l\) 变量的选择进行定义, 或者同时根据两者进行定义. 因此扩展系综模拟是系列化的副本交换形式, 单次模拟就能探索多个热力学状态.
3.16 并行
通过在多个核上并行地进行计算, 可以缩短模拟所需要的CPU时间. 理想情况下, 我们能够得到线性标度: 在 \(N\) 个核上运算就能使计算速度加快 \(N\) 倍. 但实际上, 只有当CPU核数目很少时才能达到这种效果. 计算的标度行为与所使用的算法关系很大. 此外, 不同算法对原子间的相互作用范围有不同的限制.
3.17 区域分解
由于分子模拟中的大部分相互作用都是局部的, 区域分解是分解体系的的自然方法. 在区域分解中, 每个队列分配一个空间区域, 然后对当前处于局部区域内粒子的运动方程进行积分. 使用区域分解, 你必须要做两个选择: 将单位晶胞分成多个区域和将力分配给各个区域. 绝大部分分子模拟软件都是使用半壳层方法来分配力. 但还有另外两种需要通讯更少的方法: 八壳层方法[68]和中点法[69]. GROMACS目前使用的是八壳层法, 但对于某些体系或者硬件架构来说, 中点法可能更合适. 因此, 将来我们可能会实现中点法. 绝大部分区域分解的技术细节可以在GROMACS 4的论文[5]中找到.
3.17.1 通讯坐标和力
对三斜单元晶胞的最一般情况, 我们用1D, 2D或3D格点将空间分成平行六边体, 并称其为区域分解晶胞. 每个晶胞被分配到一个粒子-粒子队列. 在每个MD步的开始, 整个体系被分到多个队列, 并在那里执行近邻搜索. 由于近邻搜索基于电荷组, 因此电荷组也是区域分解的基本单位. 电荷组被分配到其几何中心所在的晶胞. 在计算力之前, 需要对一些来自近邻晶胞的坐标进行通讯, 在力的计算完成之后, 需要将力以相反的方向进行通讯. 通讯和力的分配基于能覆盖一个或多个晶胞的区域. 图3.12展示了一个区域设置的例子.
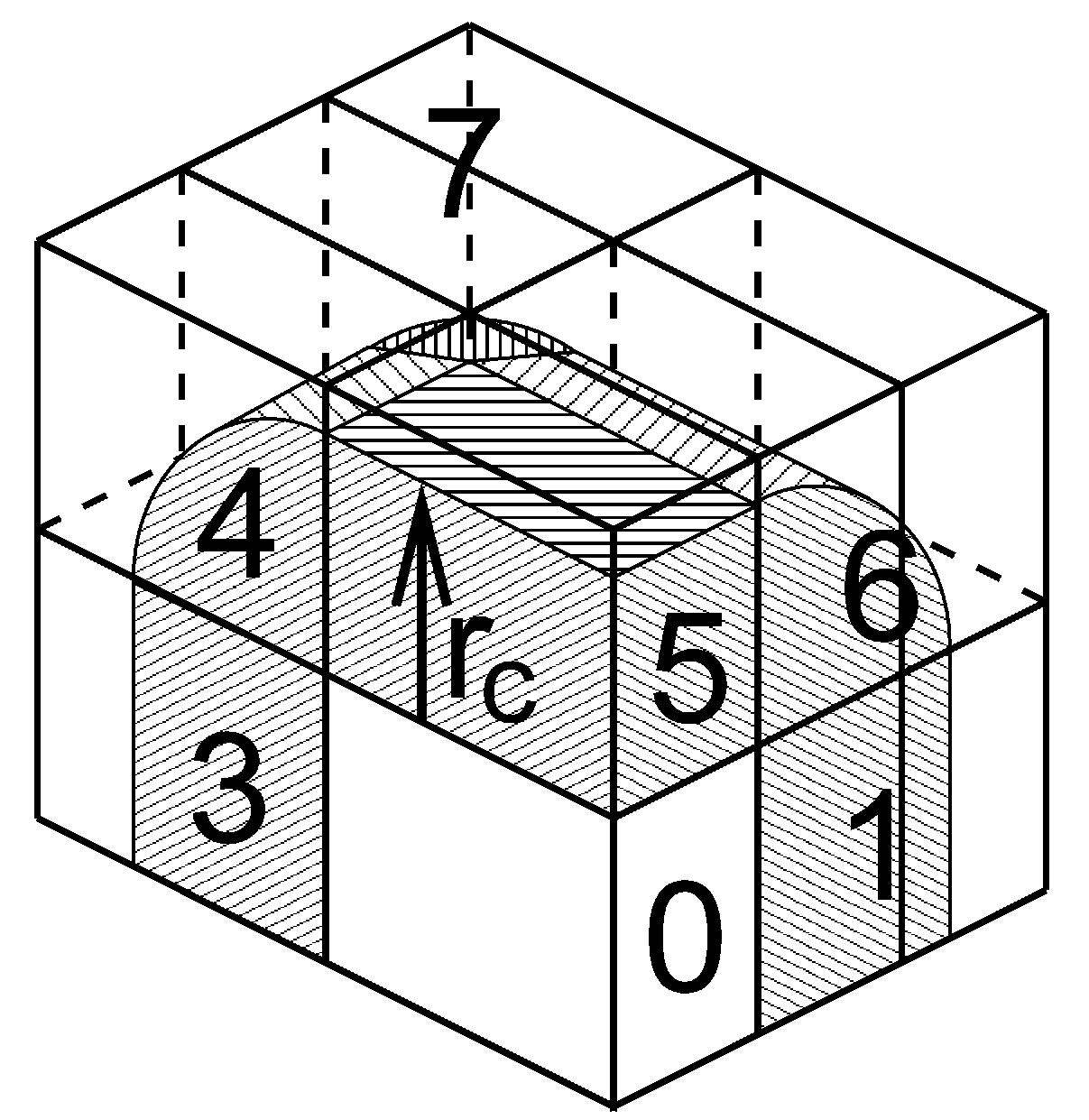
坐标通讯是通过将数据沿 \(x\), \(y\) 或 \(z\) 的“负”方向移动到下一个近邻完成的. 这可以在一个或多个脉冲内完成. 在图3.12中, \(x\) 方向需要两个脉冲, 然后 \(y\) 方向需要1个脉冲, 然后 \(z\) 方向需要1个脉冲. 而力的通讯步骤则与此过程相反. 要想了解确定哪些非键力和键合力需要在哪个队列上进行计算的细节, 请参考GROMACS 4论文[5].
3.17.2 动态负载均衡
当不同队列的计算负载不同(负载失衡)时, 所有队列都必须等待最耗时的那个队列. 这是我们极力要避免的情况. 负载失衡可能由以下三个原因造成:
- 不均匀的粒子分布
- 不均匀的相互作用计算时间分布(带电/不带电, 由GROMACS内部的水计算循环造成的水/非水计算)
- 统计涨落(仅当粒子数目较少时)
因此我们需要一个动态负载均衡算法, 它能够 独立地 调整每个区域分解晶胞的体积. 为了达到这个目的, 需要交错2D或3D区域分解的格点. 图3.13显示了2D中的最一般情况. 由于交错, 我们可能需要两个距离检查, 以决定一个电荷组是否需要通讯: 非键距离检查和键合距离检查.
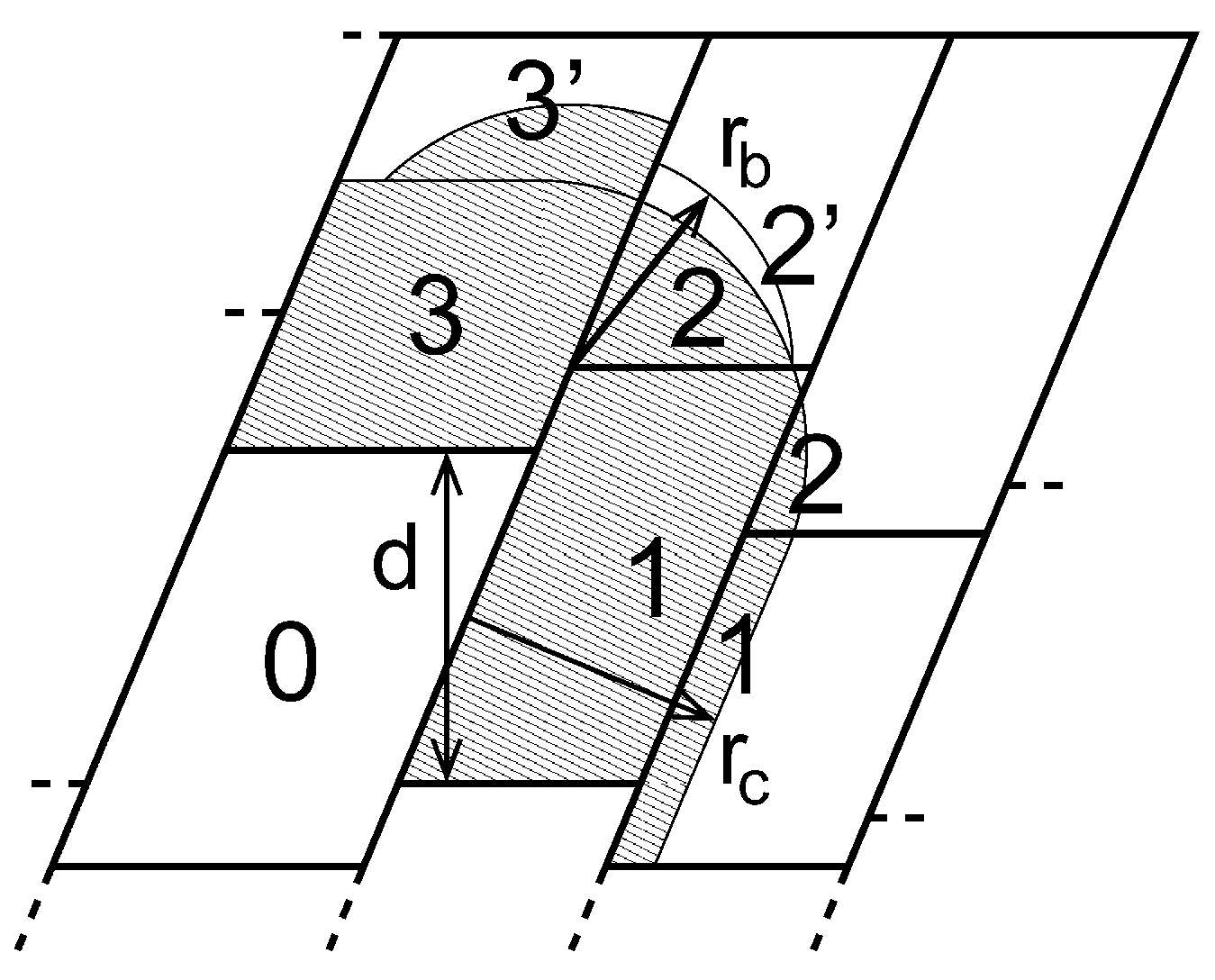
默认情况下, 在模拟中, 当由力计算失衡造成的总体性能损失达到5%或更多时, mdrun会自动开启动态负载均衡. 注意, 由于在一个积分步中, 力的计算只是所需要工作的一部分, 所以报告中力的负载失衡数据可能会偏高. 负载失衡会记录日志文件中, 输出频率由设定的日志输出步决定, 当使用-v选项时, 也会在屏幕上输出负载失衡. 平均负载失衡和由负载失衡导致的总性能损失会记录在日志文件的结尾处.
最小允许缩放比例是动态负载均衡的一项重要参数. 默认情况下, 在每个方向上区域分解晶胞至少能够缩小为原来的0.8. 对于3D区域分解, 这相当于允许晶胞的体积缩小为原来的0.5, 补偿100%的负载失衡. 这个最小允许缩放比例可以通过mdrun的-dds选项进行调整.
3.17.3 并行中的约束
由于使用区域分解时, 分子的各个部分可以处于不同的队列上, 键约束可以跨越晶胞的边界. 因此需要一个并行的约束算法. GROMACS使用了P-LINCS算法[48], 它LINCS算法[47]的并行版(参见3.6.2节). P-LINCS算法过程的示意见图3.14. 当分子跨越晶胞边界时, 会在晶胞边界中对此分子中相邻直到(lincs_order + 1)键远的原子进行通讯. 然后, 会对局部的键和通讯得到的键施加正常的LINCS算法. 经过这个步骤之后, 已经正确地被约束了局部的键, 尽管额外通讯得到的键还没有. LNICS的初始步需要一个坐标通讯步. 不需要对力进行通讯.
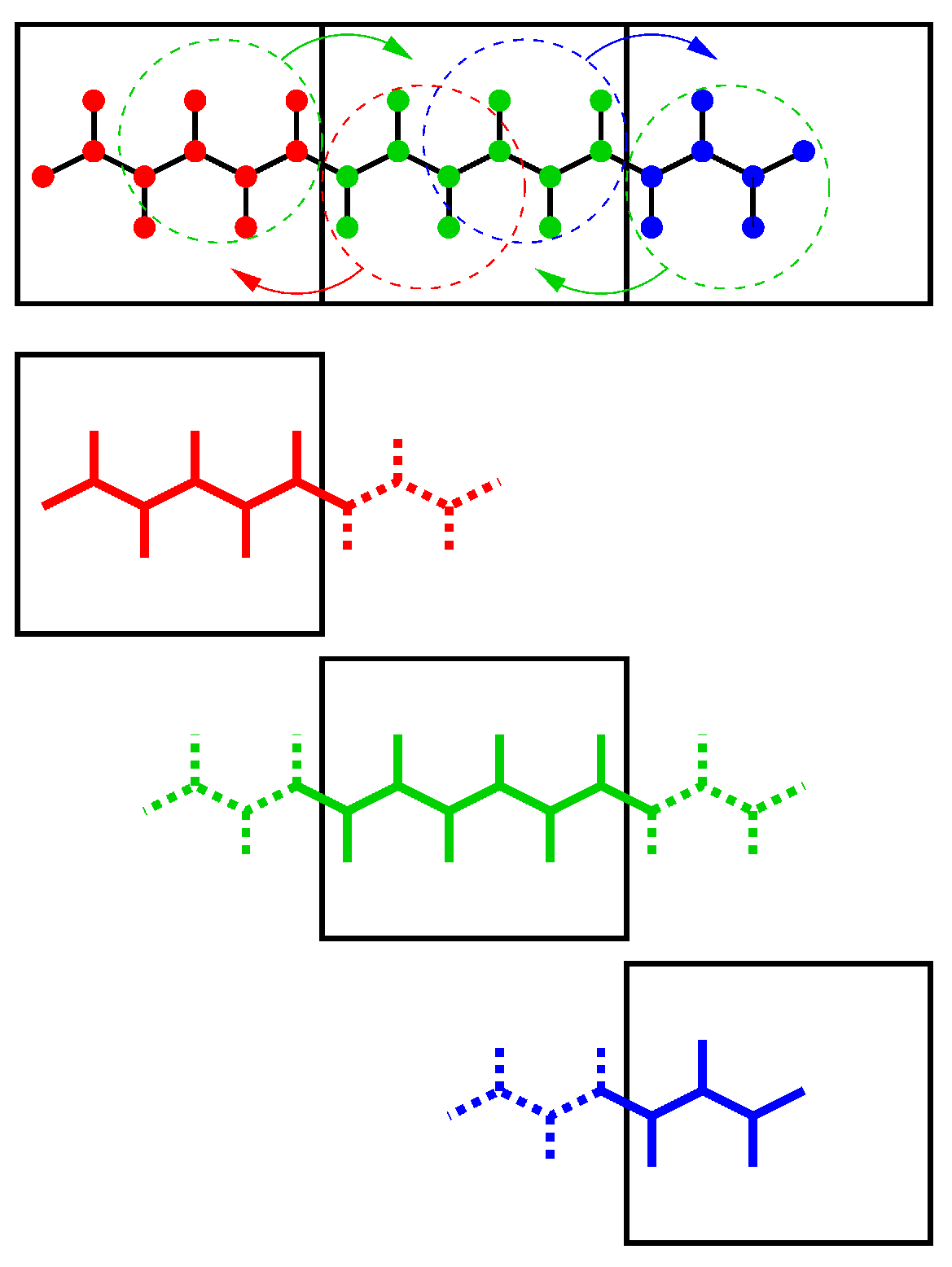
3.17.4 相互作用范围
区域分解利用了相互作用的局域性. 这就意味着对相互作用的范围有所限制. 默认情况下, mdrun程序会试着找到相互作用范围和效率之间的最佳平衡. 但也有可能发生模拟停止并给出缺失相互作用的错误信息, 或者当使用更短的相互作用范围时, 模拟运行稍微快一些的情况. 相互作用范围及其默认值都列在表3.3中.
| 相互作用 | 范围 | 选项 | 默认 | |
|---|---|---|---|---|
| 非键 | \(r_c = \max(r_\text{list}, r_\text{VdW},r_\text{Coul})\) | mdp文件 |
||
| 双体键合 | \(\max(r_\text{mb},r_c)\) | mdrun -rdd |
初始构型 + 10% | |
| 多体键合 | \(r_\text{mb}\) | mdrun -rdd |
初始构型 + 10% | |
| 约束 | \(r_\text{con}\) | mdrun -rcon |
由键长估计 | |
| 虚拟位点 | \(r_\text{con}\) | mdrun -rcon |
0 | |
在大多数情况下, mdrun的默认设置不会导致模拟停止并给出缺失相互作用的出错信息. 键合相互用作的范围由初始构型中键合的电荷组之间的距离, 再加上10%确定. 对约束, \(r_\text{con}\) 的值由(lincs_order + 1)个键所能覆盖的最大距离决定, 并且所有这些键以120度的角相连接. 实际的约束通讯并不受 \(r_\text{con}\) 限制, 而是受最小晶胞尺寸 \(L_C\) 限制:
\[L_C \ge \max(r_\text{mb}, r_\text{com}) \tag{3.147}\]
不使用动态负载均衡, 并使用压力缩放时, 实际上允许体系的缩放超过这个限制. 注意, 对于三斜盒子, \(L_C\) 并不是简单地取盒子对角分量与此方向晶胞数目的比值, 而是三斜晶胞边界之间的最小距离. 对于菱形十二面体盒子, 此距离是沿 \(x\) 和 \(y\) 方向长度的 \(\sqrt{3/2}\).
当 \(r_\text{mb} \gt r_c\) 时, mdrun会采用一个灵巧的算法以减少通讯. 如果只是简单地通讯 \(r_\text{mb}\) 之内的所有电荷组, 这将大大增加通讯次数. 因此只会对那些与不在局部出现的电荷组之间存在键合相互作用连接的电荷组进行通讯. 这将导致很少的额外通讯, 也会稍微增加区域分解设置的成本. 在某些情况下, 例如粗粒化模拟中使用非常短的截断, 可能需要手动设置 \(r_\text{mb}\) 以减小这个成本.
3.17.5 多程序多数据PME并行
静电相互作用是长程的, 因此需要使用特殊的算法来避免对许多原子对进行加和. 在GROMACS中通常使用的方法是PME(参见4.8.2节). 由于在PME算法中, 所有粒子彼此之间都存在相互作用, 因此需要全局通讯. 这通常就是区域分解标度行为的限制因素. 为了减小这个问题带来的影响, 我们提出了多程序多数据(Multiple-Program, Multiple-Data)方法[5]. 在这个方法中, 我们选择一些队列只进行PME网格计算, 而其他被称为粒子-粒子(PP)队列的队列则用于完成所有剩余的其他任务. 对于长方体盒子, PP队列与PME队列的最佳比例通常是3:1, 而对于菱形十二面体盒子最佳比例是2:1. 当PME队列的数量减少为原来的1/4时, 通讯调用的次数大约减少到原来的1/16. 或者换句话说, 现在我们可以使用4倍多的队列. 另外, 对于网络中4核或8核的现代设备来说, PME的有效网络带宽将提高4倍, 因为在PME计算中, 每个机器上只有四分之一的核在使用网络连接.
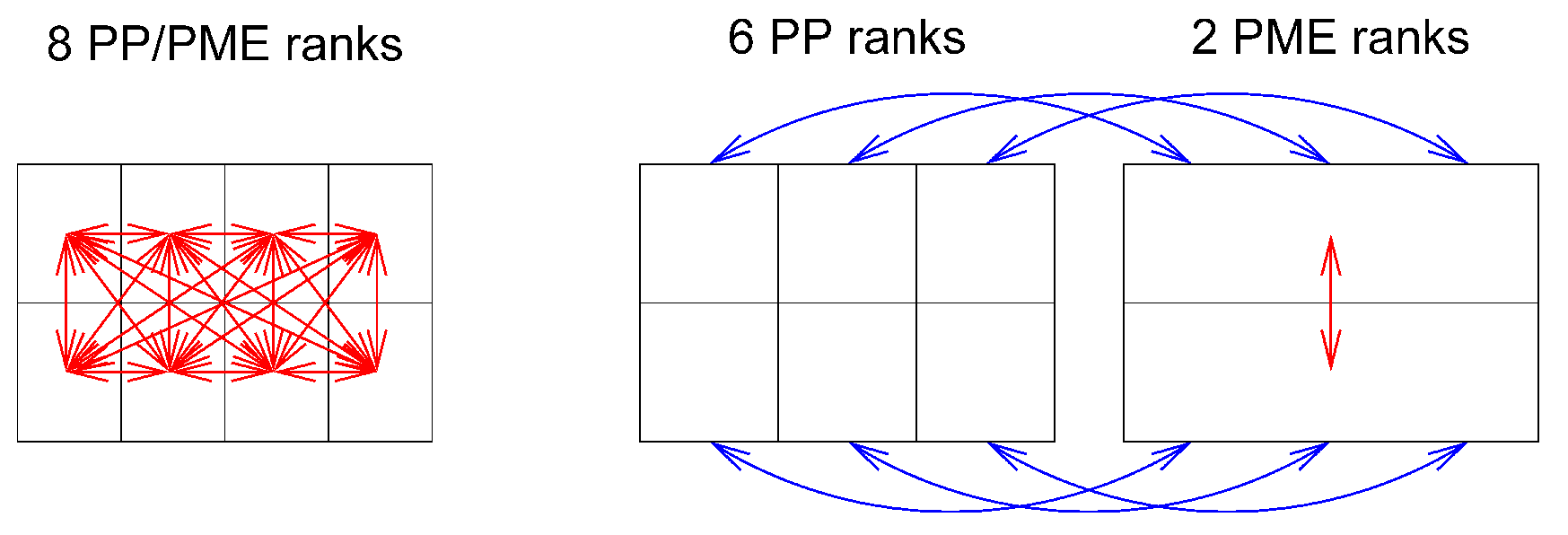
mdrun默认会交错运行PP和PME队列. 如果设备中的队列没有依次编号, 可以使用mdrun -ddorder pp_pme命令. 对带有真正的三维环及相应的合适的队列分配通讯软件的设备, 我们应该使用mdrun -ddorder cartesian命令.
为了优化性能, 我们通常应该设置截断和PME格点使得PME负载达到总计算负载的25%到33%. grompp会在末尾输出此负载的估计值, 并且mdrun也会计算相同的估计值以确定使用的PME队列的最佳数目. 对高度并行化计算, 利用mdp设置和/或由mdrun的-npme选项设定的PME队列数目来优化PME负载是值得的. 为了改变静电设置, 了解当对库仑截断和PME格点间距使用相同的比例进行缩放时, 静电的精度几乎保持不变, 对我们是很有用的. 注意, 由于PME队列数目比PP队列数目的小, 所以通常在我们估算PME队列数目的时候最好多算一些, 这样可以减少总的等待时间.
PME区域分解可以是沿 \(x\) 和/或 \(y\) 方向的1D或2D分解. 因为在高度并行化中, 2D分解的区域形状和铅笔很相似, 所以2D分解也被称为铅笔分解. 只有当PP分解沿 \(x\) 方向有唯一一个区域时, 才能使用沿 \(y\) 方向的1D分解. 2D PME分解沿 \(x\) 方向的区域数目必须等于PP分解数目. mdrun会自动选择1D或2D PME分解(当可以使用给定的全部队列数时), 基于PME中坐标再分布通讯加上格点重叠和转置通讯的最小数目. 为了避免PP和PME队列之间坐标和力的多余通讯, 理想情况下 \(x\) 方向上的DD晶胞数目应等于PME队列的数目或其倍数. 默认情况下, mdrun会考虑这些情况.
3.17.6 区域分解流程图
流程图3.16显示了区域分解中不同算法所有可能的通讯. 对于简单点的模拟, 流程图也一样, 只是不包含未使用的算法及与其相应的通讯.
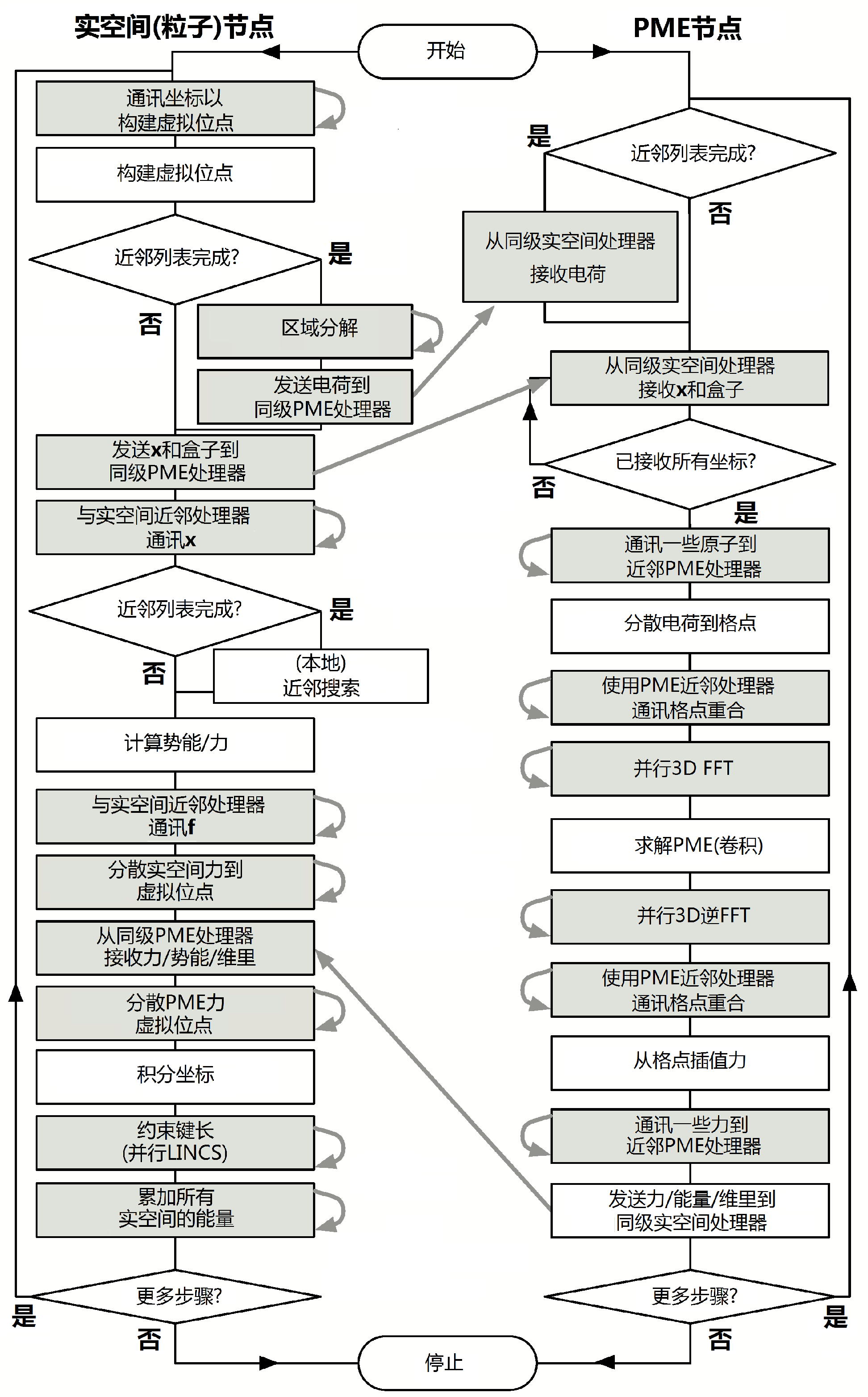
3.18 隐式溶剂模型
隐式溶剂模型提供了一种表现溶剂分子静电效应的有效方式, 同时避免了分子动力学模拟中的大量计算, 这些计算涉及对周围水分子进行精确的, 溶剂化的描述. 与显式溶剂模型相比, 隐式溶剂模型有以下几个优点: 不需要对溶质周围的水分子进行平衡; 不存在粘度, 蛋白质能够更快地探索构象空间.
GROMACS中的隐式溶剂计算利用广义Born公式, Born半径的计算可使用Still[70], HCT[71]和OBC[72]模型.
溶剂化自由能 \(G_\text{solv}\) 是三项的加和, 溶剂-溶剂空穴项(\(G_\text{cav}\)), 溶质-溶剂范德华项(\(G_\text{vdw}\)), 还有溶质-溶剂静电极化项(\(G_\text{pol}\)).
\(G_\text{cav}\) 和 \(G_\text{vdw}\) 的总和对应于移除所有电荷的分子所具有的(未极化)溶剂化自由能, 通常称作 \(G_\text{np}\), 等于总的溶剂可及表面积乘上表面张力. 因此溶剂化自由能的总表达式可写为:
\[G_\text{solv}=G_\text{np}+G_\text{pol} \tag{3.148}\]
对于广义Born模型, \(G_\text{pol}\) 可由广义Born方程计算[70]:
\[G_\text{pol}=\left(1-{1\over \e}\right) \Sum_{i=1}^n \Sum_{j \gt i}^n {q_i q_j \over \sqrt{r_{ij}^2+b_i b_j \exp\left({-r_{ij}^2 \over 4 b_i b_j}\right)} } \tag{3.149}\]
在GROMCAS中, 我们引入了代换[73]:
\[c_i={1\over \sqrt{b_i} } \tag{3.150}\]
这样当计算每项相互作用时, 可以引入新变量 \(x\)的简单变换:
\[x={r_{ij} \over \sqrt{b_i b_j} }=r_{ij} c_i c_j \tag{3.151}\]
最后, 改写后3.149的完整的公式如下:
\[G_\text{pol}=\left(1-{1\over\e}\right)\Sum_{i=1}^n \Sum_{j \lt i}^n {q_i q_j \over \sqrt{b_i b_j} } \x(x)=\left(1-{1\over\e}\right)\Sum_{i=1}^n q_i c_i \Sum_{j \lt i}^n q_j c_j \x(x) \tag{3.152}\]
方程3.148的非极化部分(\(G_\text{np}\))直接根据每个原子的Born半径计算, 计算时使用了Schaefer等人提出的简单ACE类型近似[74], 并包含了对所有原子的一个简单循环. 这只需要一个额外的溶剂化参数, 与原子类型无关, 但三种Born半径模型之间有稍微的差别.
